截錐形彈體在液體介質中運動速度衰減規律分析*

孔祥韶，石 干，王旭陽,3，周紅昌，吳衛國

（1. 武漢理工大學綠色智能江海直達船舶與郵輪游艇研究中心，湖北 武漢 430063；2. 武漢理工大學交通學院，湖北 武漢 430063；3. 西安航天動力研究所液體火箭發動機技術重點實驗室，陜西 西安 710100）

大型水面艦艇通常采用液艙來防護反艦武器爆炸破片對內部結構和人員的威脅[1]。彈體在侵徹液艙過程中與液體的作用機理十分復雜，彈體在液體介質中的貫徹距離、速度衰減規律以及高速彈體引起的水錘效應，是廣大學者長期關注的問題，對此已開展了大量的研究。Lee 等[2]在經典沖擊壓力模型的基礎上，將彈體簡化為點源，對高速彈體在液體中引起的空腔效應展開了研究，推導建立了空腔動力學方程。李營等[3]在考慮長徑比的影響下，將阻力因數作為與初速度有關的常量來處理，擬合得到了阻力因數計算經驗公式。沈曉樂等[4]考慮彈體的墩粗變形進行了實驗研究，對方形彈體入水的阻力因數進行了修正。郭子濤[5]分析了彈頭形狀對彈體水彈道穩定性以及速度衰減規律的影響，提出了一種簡化的彈體頭型阻力因數估算公式。Zhao 等[6]在考慮雷諾數的基礎上對球形彈入水阻力因數進行擬合，提出了球形彈入水阻力因數經驗公式。Zhang 等[7]在Lee 等[2]研究工作的基礎上針對長徑比在0.1～0.5 之間的餅形彈進行研究，并對餅形彈入水阻力因數計算公式進行了修正。這些研究普遍簡化了阻力因數的影響因素，與實際物理過程有較大的區別。

本文中，擬采用理論分析和數值模擬的方法，針對以上存在的問題，開展截錐形彈體垂直穿透液體介質時的速度衰減特性研究，重點分析不同彈體頭形因數對其速度衰減規律的影響，以期建立阻力因數與彈體的瞬時速度之間的關系，并引入彈體形狀參數的影響，建立截錐形彈體在液體中的速度衰減分析模型。

1 彈體侵徹液體介質速度衰減規律

當彈體在液體介質中高速運動時，彈體損失的動能主要轉化為液體的動能及空泡的壓力勢能，而空泡的存在極大地減小了彈體與液體的接觸面積，從而彈體運動所受的摩擦阻力減小，因此壓差阻力是影響彈體阻力的主要因素。則根據牛頓第二定律建立彈體運動方程如下[8]：

2 數值計算

2.1 數值計算工況設計及模型

本節設計4 種不同頭形因數的截錐形彈體，采用顯式動力學非線性有限元程序Autodyn 建立彈體的仿真模型并開展系列工況的數值計算，分析頭形因數對彈體垂直入水后速度衰減的影響規律。

圖1 為截錐形彈體示意圖，定義彈體頭部圓臺直徑D2與主體最大直徑D1的比值D2/D1為截錐形彈體頭形因數 ψ 。各工況中彈體主體長度L1=30 mm ，錐體長度L2=10 mm ，主體直徑D1=12 mm 保持不變，4 種彈體頭部圓臺直徑分別為0、4、8、12 mm，對應頭形因數 ψ1～ψ4分別為0、1/3、2/3、1。為了控制變量的數量，不同頭形因數截錐形彈體的質量均調整為32.5 g，有限元模型如圖2 所示。本次數值模擬采用二維軸對稱建模方法，水域網格尺寸為400 mm×400 mm，采用邊長為1 mm 的四邊形歐拉單元進行離散，四周設置透射邊界條件，模擬無限水域，彈體用拉格朗日網格離散。

數值模擬中，采用S h o c k 狀態方程和Johnson-Cook 本構關系描述彈體材料的動態力學行為[12]：

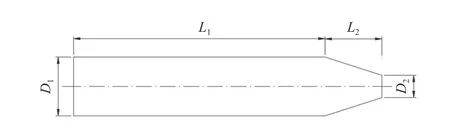
圖 1 截錐形彈體示意圖Fig. 1 Schematic diagram of a truncated cone-shaped projectile

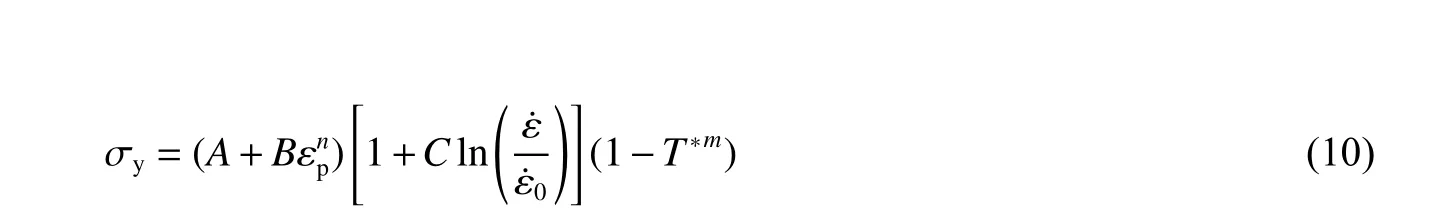
式中： σy為材料的動態屈服應力；A為材料的靜態屈服應力；B為材料的硬化參數； εp為等效塑性應變；n為硬化指數；C為應變率參數；ε ˙ 為等效塑性應變率；ε ˙0為參考應變率，取 ε ˙0=1 s-1；T*=(T-Tr)/(Tm-Tr) ，T為溫度，Tr為室溫，Tm為材料熔化溫度，m為溫度指數。本文中彈體材料選用45 鋼[13]，A為506 MPa，B為320 MPa，n為0.28，C為0.064，m為1.06，Tm為1 750 K。

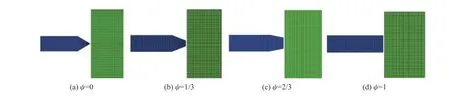
圖 2 不同頭形因數截錐形彈體有限元模型Fig. 2 Finite element models for truncated cone-shaped projectiles with different head type coefficients

表 1 水的狀態方程各項參數[14]Table 1 Parameters of equation of state for water[14]

本文中對每種不同頭形因數的截錐形彈體各設置了5 種不同的入水初速度開展數值模擬，共包含20 種工況條件，如表2 所示。

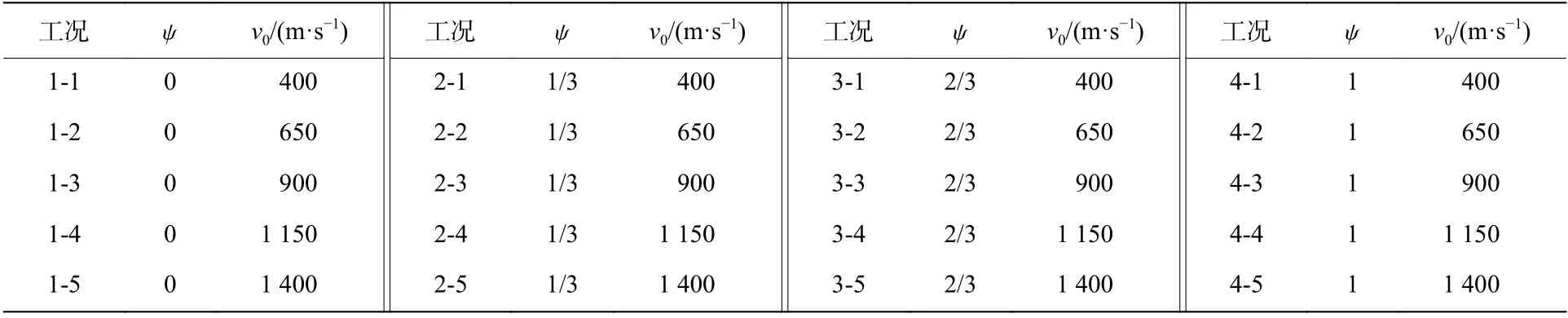
表 2 數值計算工況Table 2 Numerical calculation conditions

2.2 有限元方法驗證

采用本文的數值模擬方法對試驗過程[5]開展計算，通過對比分析數值計算結果和試驗數據來驗證數值方法對高速彈體入水過程分析的可靠性和準確性。文獻[5]中使用輕氣炮發射圓柱形平頭彈體，該彈體直徑D=12.65 mm，長度L=25.4 mm，入水初速度為603 m/s，試驗中使用高速攝影儀記錄了彈體運動軌跡及空泡變化，測量了不同時刻的空泡尺寸以及彈體速度等數據。將數值模擬得到的高速彈體入水過程中與試驗[5]中相應的數據進行對比，彈體入水后空泡尺寸對比如圖3 所示，可以發現在t=0.222 ms和t=0.440 ms 時刻相同位置處的空泡直徑數值計算結果與試驗測量數據吻合較好

圖 3 針對彈體直徑為12.65 mm，長度為25.4 mm，入水初速度為603 m/s 時，試驗與數值計算的空泡尺寸Fig. 3 Comparison of cavitation sizes obtained experimentally and numerically for the projectile with the diameter of 12.65 cm and the length of 25.4 cm, water entering at 603 m/s

此外，進一步開展尺寸D=12.65 mm，L=25.4 mm 的平頭圓柱形彈體入水速度603 m/s 及397m/s 工況；D=12.65 mm，L=38.1 mm 的平頭圓柱形彈體入水速度為498 m/s 及414 m/s 工況的數值計算，將彈體位移隨時間的變化以及彈體速度衰減的數值計算結果與相應的試驗測量數據進行對比，如圖4～5 所示。可以看出，本文數值模擬方法在計算彈體的運動特性方面具有較好的精度，可為本文的進一步的研究工作開展提供了準確可靠的分析手段。

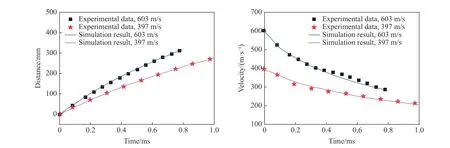
圖 4 長度為25.4 mm 的彈體在兩種入水速度工況下位移和速度的變化Fig. 4 Changes of displacement and velocity of the projectile with the length of 25.4 mm at two initial velocities of water entry

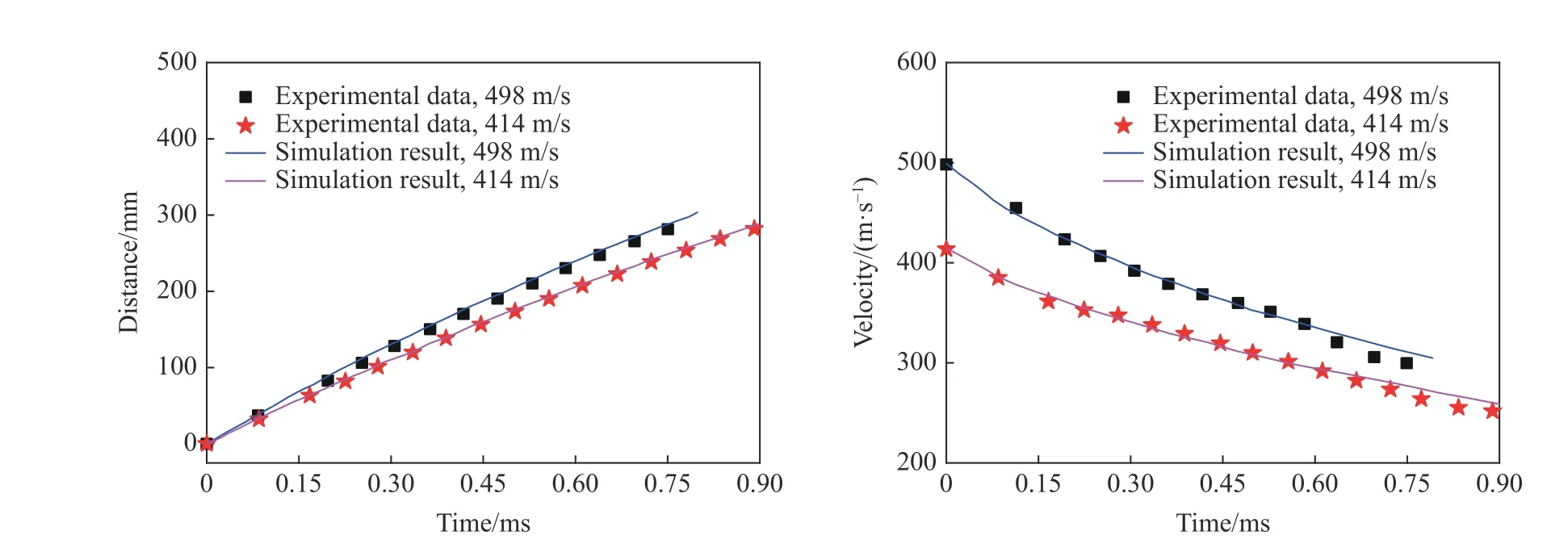
圖 5 長度為38.1 mm 的彈體在兩種入水速度工況下位移和速度的變化Fig. 5 Changes of displacement and velocity of the projectile with the length of 38.1 mm at two initial velocities of water entry

2.3 數值模擬結果及分析

采用驗證后的數值模擬方法開展表2 中20 種工況的數值計算，將頭形因數不同的截錐形彈體在不同入水速度下的速度衰減與入水距離的關系繪制于圖6，通過對比分析圖中數據可以發現：

（1）當截錐形彈體的頭形因數不變時，彈體入水后速度變化曲線的斜率隨著入水初始速度的升高而逐漸增大，說明入水速度越高，速度衰減越快；

（2）彈體入水初速度不變、頭形因數增大時，彈體剩余速度并非單純隨頭形因數增大而降低，這一特性在v0=1 400 m/s 時表現最明顯。4 種頭形因數的彈體均以1 400 m/s 的初速度垂直入水時，運動400 mm后彈體剩余速度與初速度的比值vb/v0分別為0.699 0、0.771 0、0.709 9、0.512 7。說明入水初速度不變時，隨著彈體頭形因數的增大，vb/v0呈現先增大后減小的趨勢，在 ψ =1/3 時達到最大，為0.771。

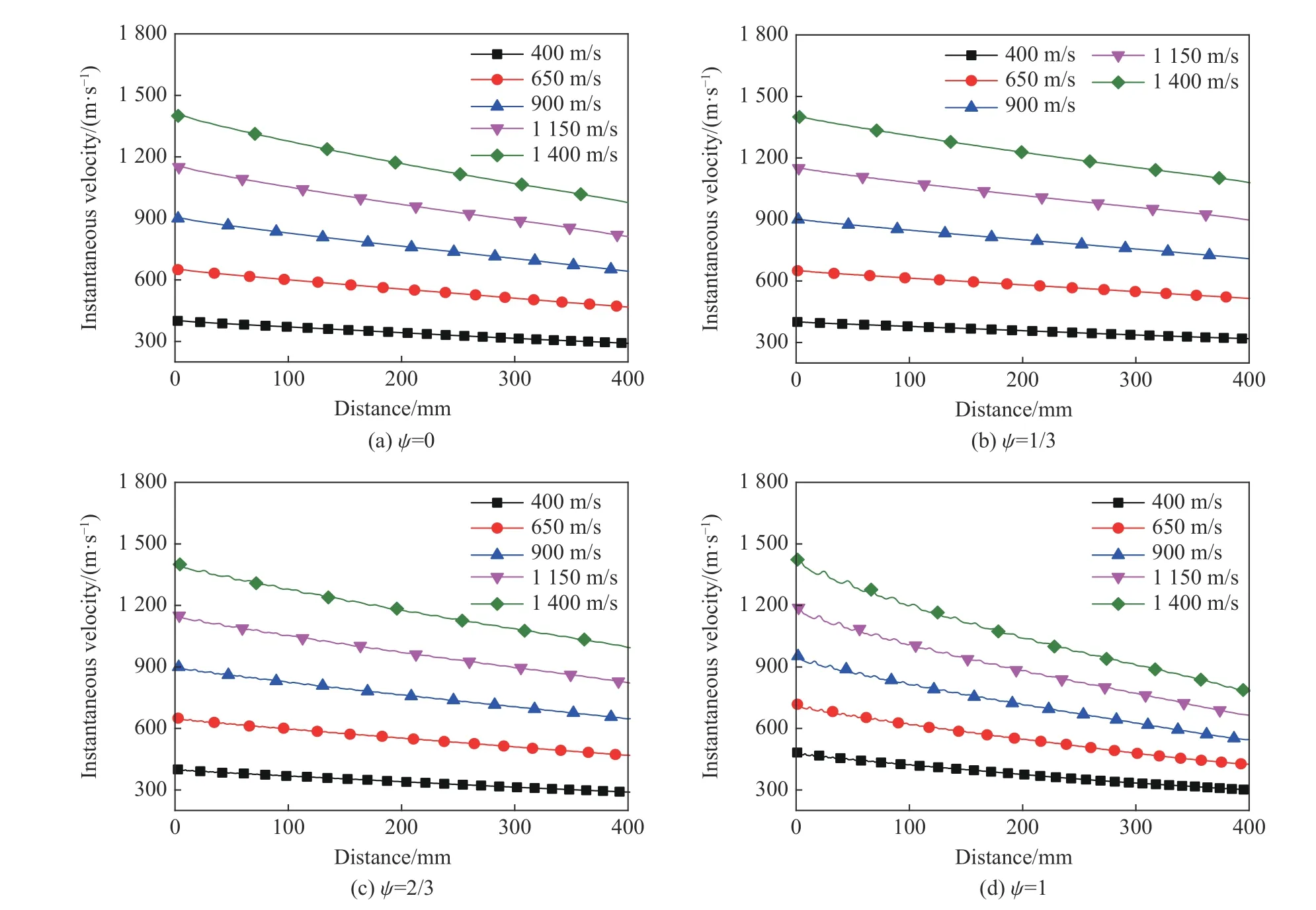
圖 6 不同頭形因數的截錐形彈體在不同入水速度工況下速度隨入水距離的衰減Fig. 6 Velocity attenuation of truncated cone-shaped projectiles with different head coefficients with water-entry distance at different initial velocities of water entry

3 速度衰減分析模型

3.1 模型建立

根據式（4）可以計算得出截錐形彈體垂直入水后的瞬時阻力因數Cd，并將其作為縱坐標，將彈體的瞬時速度vb與入水初速度v0的無量綱比值作為橫坐標，繪制Cd- (vb/v0) 關系圖。由于篇幅有限，本文中僅繪出ψ=0 的彈體Cd- (vb/v0) 關系圖，如圖7 所示。從圖7 可以發現，阻力因數Cd隨著彈體速度的衰減呈振蕩趨勢，且當截錐形彈體速度較低時，隨著侵徹過程的進行，速度衰減率出現較小幅度的上升。究其原因是因為隨著速度的降低，彈體誘導空泡的尺寸也在不斷減弱，彈液間的接觸面積增大，摩擦阻力增大，導致彈體的速度衰減率和阻力因數Cd小幅增大。

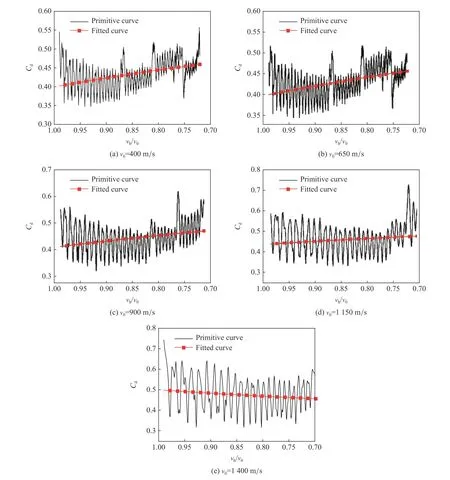
圖 7 不同入水速度下， ψ =0 的截錐形彈體阻力因數與 v b/v0 的關系Fig. 7 Resistance factor varying with v b/v0 for the truncated cone-shaped projectile with ψ=0 at different water-entry velocities

從完整的侵徹過程來看，阻力因數Cd變化過程較復雜，阻力因數隨著彈體速度的降低，呈現如上述圖像所示的震蕩變化趨勢。在以往的研究方法中將其作為常量來處理，不具備廣泛的適用性。從簡化計算的角度出發，本文中采用線性關系進行擬合：

式中：a0和a1為未知參數。

針對圖7 中的數據，采用最小二乘法進行擬合，擬合的結果如圖7 中紅線所示。同時，對頭形因數ψ=1/3 ， ψ =2/3 ， ψ =1 的 截錐形彈體數據按照同樣方式進行擬合，確定的參數a0和a1列于表3。

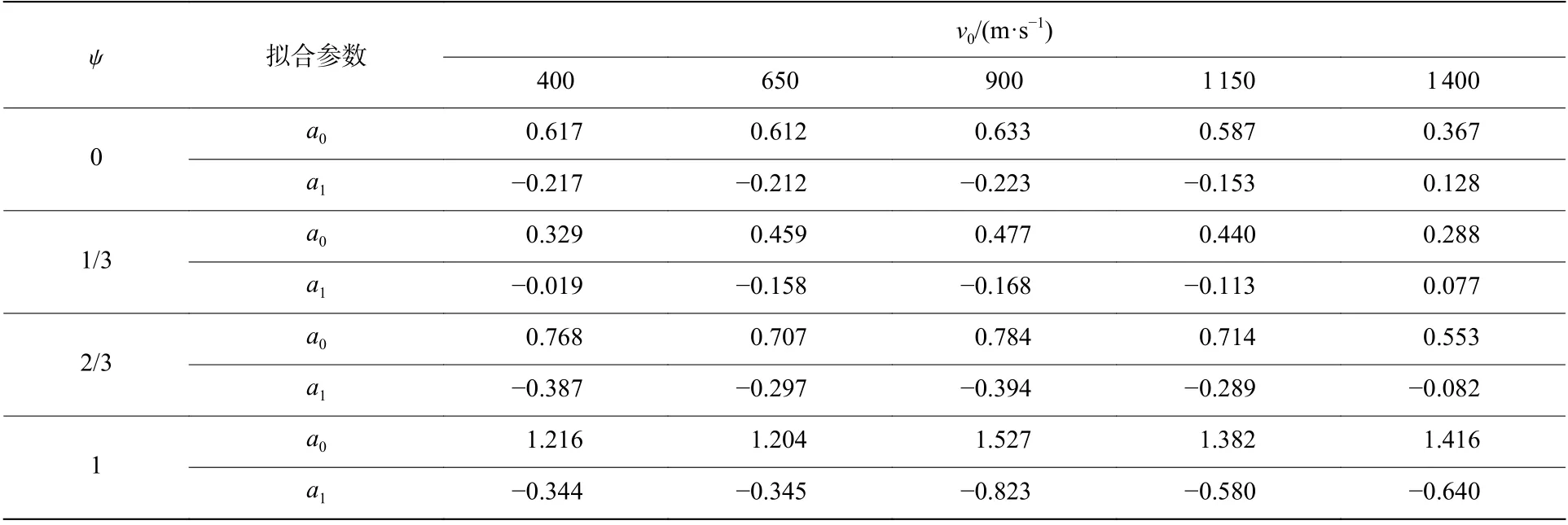
表 3 不同工況下的參數 a0 和 a1 的數值Table 3 Values of parameters a0 and a1 under different working conditions

水中聲速取1 400 m/s，用最小二乘法對參數a0和a1進行擬合：

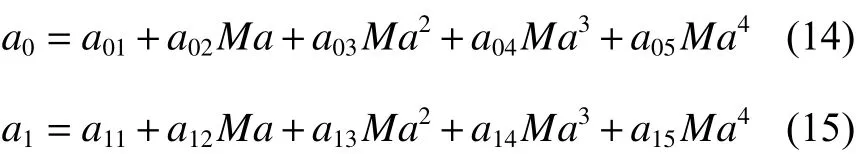
式中：a01、a02、a03、a04、a05、a11、a12、a13、a14、a15為待定參數，結果如圖8 所示。

由擬合結果來看，四階方程可以較好的擬合a0、a1關于無量綱數M的關系，可以發現同一頭形因數下參數a0及a1的高度相關，但變化趨勢相反，近似關于某一水平線y=n1對稱。隨著頭形因數的增大，參數a0及a1的變化逐漸趨于復雜，這是因為當頭形因數增大時，彈體的垂直迎流面積增大，侵徹時鐓粗變形效應變得明顯，導致阻力因數的變化趨于復雜。參數a0、a1的擬合結果列于表4。

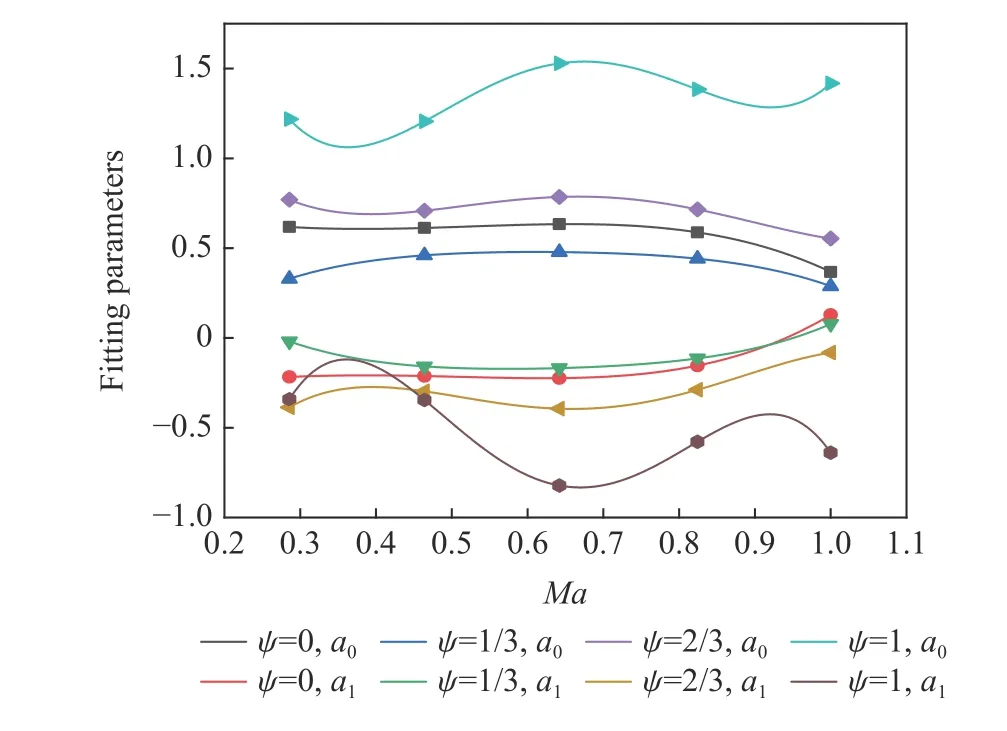
圖 8 對于頭形因數不同的截錐形彈體，參數a0 和a1 與馬赫數 Ma 的關系Fig. 8 Changes of parameters a0 and a1 with Mach number Ma for the truncated cone-shaped projectiles with different head shape factors

表 4 參數 a0 、 a1 的擬合結果Table 4 Fitting results of parameters a0 and a1

圖 9 a 系列參數與頭形因數 ψ 的關系Fig. 9 Series parameters of a varyied with head shape factor ψ

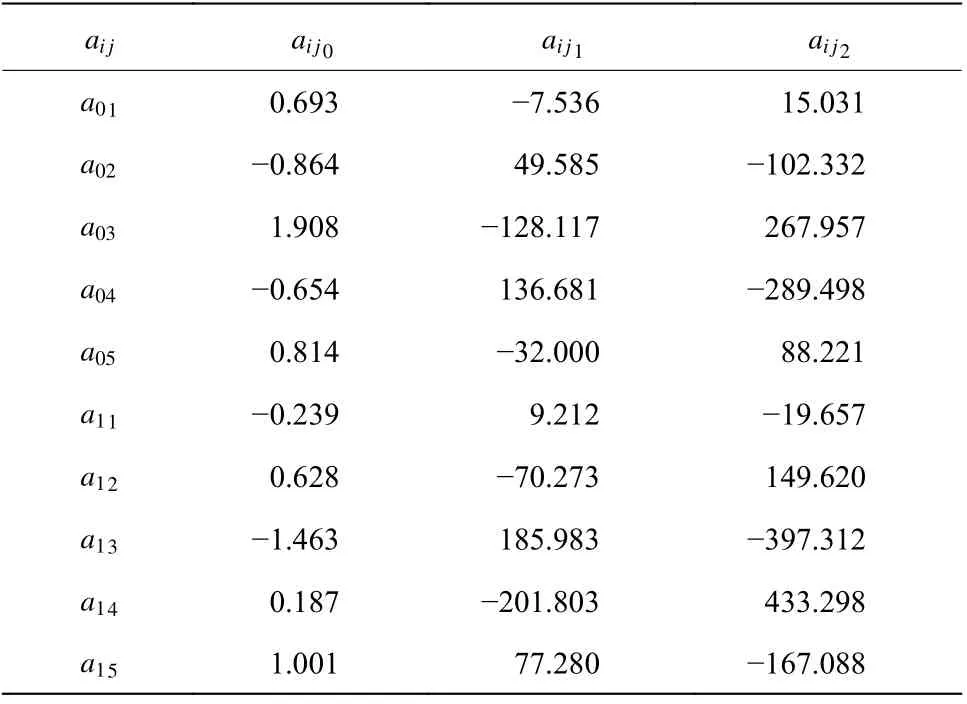
表 5 ai j 系列參數的擬合結果Table 5 Fitting results of ai j series parameters

綜上所述，當頭形因數 ψ 不同的截錐形彈體垂直侵徹入水時可以通過如下公式計算實時阻力因數Cd：

3.2 算例分析及驗證

通過2.2 節中已驗證的計算方法開展系列模擬計算，通過對公式（18）的編程求解，得到彈體的速度衰減。將數值計算結果與上述速度衰減模型計算結果進行對比，驗證其可靠性。

驗證計算中，設置v0=400 m/s 速度下1/6、1/2、5/6 等3 種頭形因數工況以及頭形因數為 ψ =1/6 的彈體在100～600 m/s 區間內6 種入水速度工況進行驗證計算，結果如圖10～11 所示。

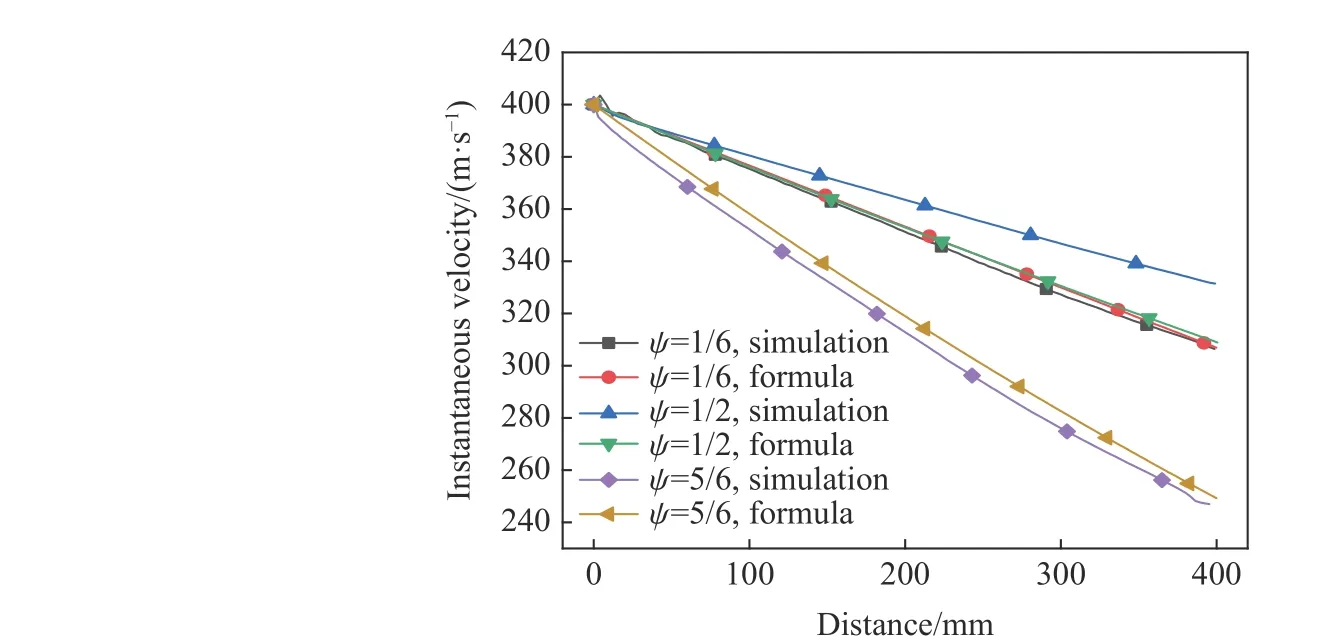
圖 10 入水速度為400 m/s，頭形因數不同的彈丸，速度隨入水距離衰減的模擬結果與公式計算結果的比較Fig. 10 Comparison of velocity attenuation with distance between numerical simulation and formula calculation for the projectiles with different head shape factors at the initial water-entry velocity of 400 m/s

由計算可以發現，對于彈徑相同、入水初速相同而頭形因數不同的彈體，其速度衰減規律有著顯著差異。本文的計算分析模型中考慮了因頭形因數不同而引起的阻力因數變化對彈速衰減的影響，與數值計算結果吻合較好。當彈體入水初速為400 m/s，頭形因數為1/2 時，數值計算數據與本文公式計算結果之間的誤差約為6.8%，其他兩種頭形因數工況下誤差更小；在彈體頭形因數為1/6、不同速度工況中，公式計算與數值模擬結果之間的最大誤差約為8.71%。

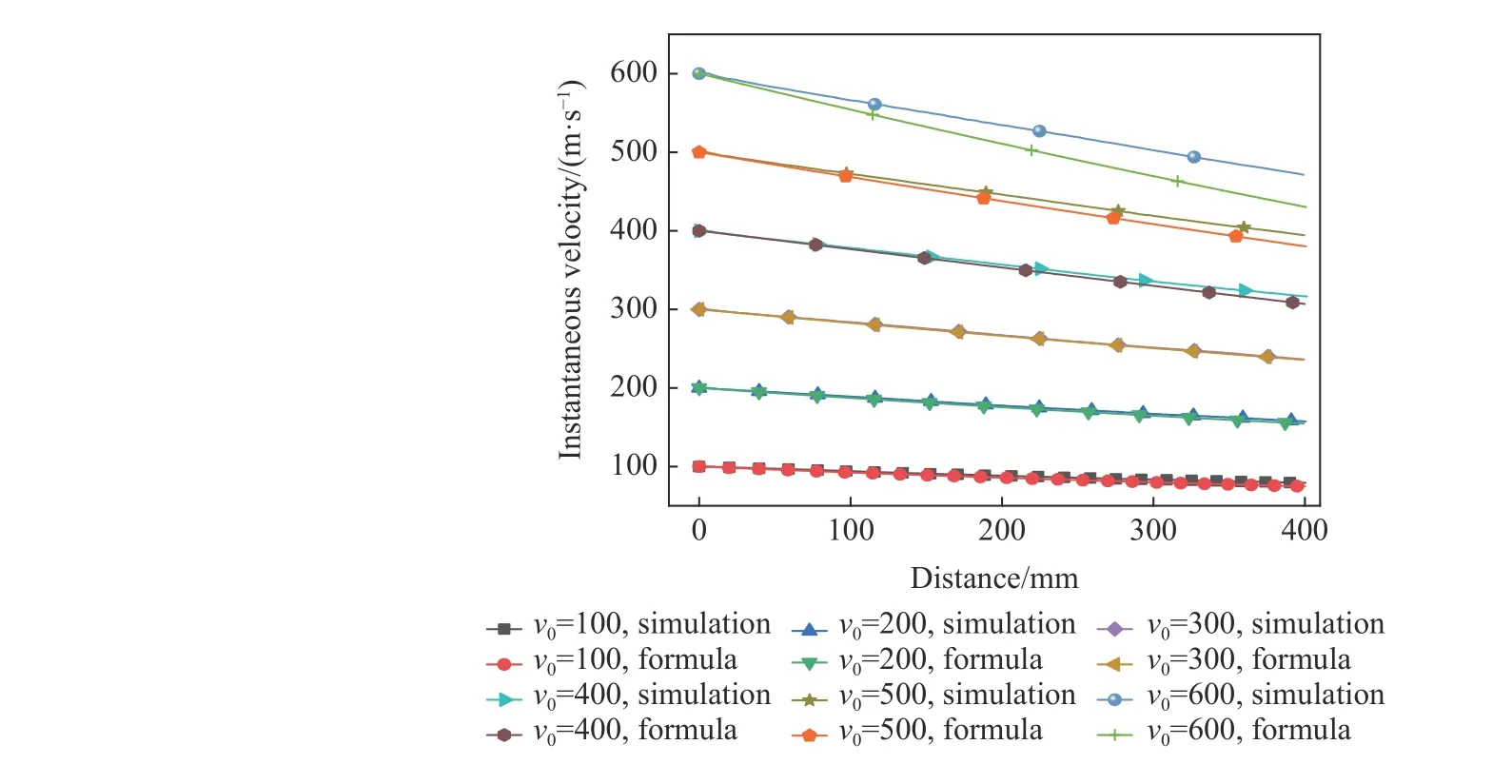
圖 11 頭形因數為1/6，入水速度不同的彈丸，速度隨入水距離衰減的模擬結果與公式計算結果的比較Fig. 11 Comparison of velocity attenuation with distance between numerical simulation and formula calculation for the projectile with the head shape factor of 1/6 at different initial water-entry velocities

從上述對比結果可以發現，本文的速度衰減模型可對不同頭形因數的截錐形彈體垂直侵徹液體介質過程中的速度衰減進行快速預報，彌補了以往研究中將阻力因數Cd當作常量計算的不足，更符合彈體垂直侵徹液體介質的實際物理過程。

4 結 論

本文中提出了與彈體形狀和無量綱速度相關的阻力因數的計算方法，通過建立運動方程得到了截錐形彈體垂直侵徹液體介質速度衰減的計算分析模型。并通過算例分析，驗證了本文計算方法的可靠性。得到以下結論：

（1）高速彈體在液體介質中運動方程的阻力因數與彈體形狀和無量綱速度有關；該因數對彈體高速運動過程中與液體的接觸面積進行了修正，將彈體頭形因數和速度因素考慮在內，更接近實際的物理過程。

（2）將阻力因數引入運動方程后得到的計算結果與數值模擬數據吻合較好, 說明本文提出的分析模型可對不同頭形因數的截錐形彈體垂直侵徹液體介質過程中的速度衰減進行快速預報。

（3）由于彈體侵徹液體時的作用機理非常復雜，且彈體高速侵徹時會發生彈體鐓粗和變形，同時流體具有可壓縮性，對彈速衰減影響較大。本文的分析中未考慮其影響，在后續工作中將進一步的深入研究。