一種對抗全局竊聽的網絡編碼方案*

周 影，褚麗莉，陳 佳

（遼寧工業大學，遼寧 錦州 121000）

0 引言

網絡編碼理論[1]的提出，為數據傳輸帶來了深刻的影響，相比路由單一的存儲轉發功能，網絡編碼通過節點對上游數據進行存儲—編碼—轉發，從而提高網絡吞吐量、魯棒性[2]和安全性。

網絡編碼在提升數據傳輸能力的同時，網絡仍具有被監聽的風險。針對抗竊聽安全網絡編碼，對抗竊聽攻擊的方法主要有兩種：信息論方法和密碼學方法。Cai 等人利用傳統信息論方法對抗網絡編碼中的竊聽攻擊[3]，從而使竊聽攻擊者竊聽到網絡中的任意一個竊聽子集均無法通過其譯碼恢復出原始消息向量。在此基礎上，文獻[4]中進一步提出了r-安全網絡編碼方案，但該方案提出的前提是竊聽鏈路數少于竊聽網絡鏈路的最大值，且不適用于多源網絡。因此利用信息論實現對抗竊聽的編碼方案必須具備限制條件，即限定竊聽者的竊聽能力。

相比信息論對抗竊聽攻擊的局限性，基于密碼學抗竊聽方案更具優勢。Zhang 等人[5]提出了一種P-Coding 抗竊聽安全網絡編碼方案，該方案利用一個置換函數將全局編碼系數和編碼后的消息向量進行混合和重新排列，從而無法正確譯碼出原始數據，達到抗竊聽的目的。但是需要對整個信源消息加密，并且該方案無法抵抗已知明文攻擊。Fan 等人[6]利用同態加密的方法隱藏全局編碼系數，從而使竊聽者無法竊聽信源消息，但是此方案要求在較大的有限域內進行編解碼，導致計算復雜度偏高。

綜上所述，本文提出一種新的抗全局竊聽的安全網絡編碼方案，該方案不會增加寬帶消耗，并且不改變中間節點的編碼方式，對信源組播率沒有要求。分析表明該方案可以達到安全網絡編碼的要求。

表1 各節點端口號以及對應端口接收的消息

1 基本模型與概念

1.1 隨機線性網絡編碼網絡模型

對于一個多元多宿網絡結構G=(V,E),其中V代表網絡中的節點集，E代表有向邊集，節點集合包含三部分，分N={N1,N2,…,Nm}別為信源節點集合S={S1,S2,…,Sn}，中間節點集合，

信宿節點集合R={R1,R2,…,Rk}，根據網絡結構，確定信源節點Si的傳輸速率mi，每個信源節點的傳輸速率決定了多播容量。信源節點Si發送m條消息至信宿節點，消息長度為n,信源消息為xi。

多源隨機網絡編碼是不同于單源網絡編碼的含有多源多宿的網絡結構，對于一個多源多宿網絡[7]，源節點間的組播率相互約束，利用枚舉法求得網絡模型的可達信息率域邊界C={(1,4),(2,3),(3,2),(4,1)}，為了不重復贅述兩個信源的構造方法，選取區域內的的組播率都為2[8]。

1.2 竊聽模型

（1）考慮多信源多信宿。

（2）竊聽者可以對網絡中的所有信道進行竊聽，即竊聽者為全局竊聽者。

（3）竊聽者知道網絡中的整個編解碼方案和消息傳輸方案，但無法獲得加密密鑰。

（4）本通信模型只考慮竊聽攻擊。

（5）密鑰分配中心(KDC)為源節點和信宿節點分配密鑰。

2 混沌系統

混沌系統是指存在于一個確定性系統中看似隨機的不規則運動,其行為具有不確定性、不可重復性、不可預測性。混沌系統對初始狀態和控制參數極其敏感[9]。其中，Logistic 映射屬于一維混沌系統[10]，又稱為蟲口映射。由May 在1976 年提出，用來統計昆蟲或者人口數量變化的一個簡單的數學模型[11]，其表達式如（1）所示：

其中，n=1,2,3,…，參數μ表示控制參量μ∈(0,4]，變量xn∈[0,1]。

研究發現，當xn∈[0,1]，μ∈(3.569,4]時，系統處于非收斂狀態，圖2 為Logistic 分叉圖。

圖2 Logistic 分叉圖

3 編碼方案

首先利用Logistic 混沌系統生成預編碼系數矩陣，通過除法運算G生成所要傳輸的消息；將消息以隨機網絡編碼的方式發送到下游節點；最終在信宿節點進行譯碼操作。編碼方案流程圖如圖3 所示。

3.1 參數分配

混沌系統具有不可預測性，相差微小的兩個初值，經過迭代后產生的數組相差甚遠，且得到的結果不能計算出原始數據，根據該特性，初始值以及參數作為logistic 加密的密鑰。

3.2 信源編碼方案

首先，利用logistic 系統產生小數向量Y={y1,…,ym}，選取yi中的第2.4.6.8.10 位構成一個整數ti，此時ti的位范圍為0 到99999，m個ti組成一個整數矩陣，形式如下：

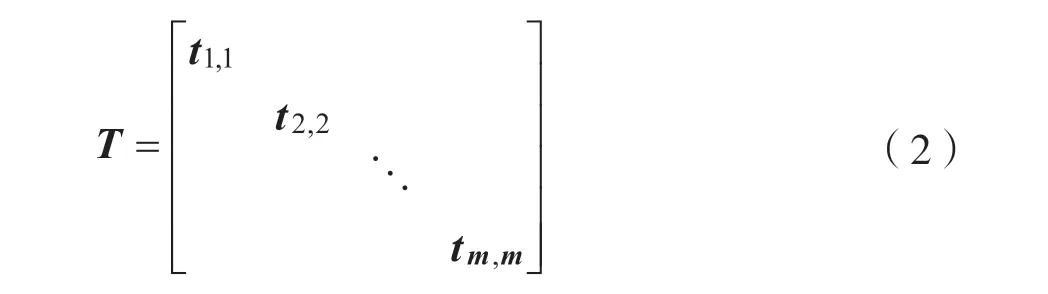
圖3 編碼方案流程圖

通過公式（3）計算得出帶有信源消息的大數非整數矩陣Z：

利用Z對信源消息進行隱藏，得到的結果矩陣為A：

為了使消息在有限域中F28進行運算，將A變成整數，通過256 進行除法操作，得到商矩陣Qu和余數矩陣Re。通過AES 加密算法對Qu行加密成為E(Qu)，Re 序列作為被編碼消息進行網絡編碼，最后以Data=[α|C|E(Qu)]形式傳遞給中間節點，其中α為系數矩陣，C為編碼結果矩陣。

3.3 信宿節點解碼

（1）信宿節點收到數據后，對m個非線性系數向量和結果向量進行組合，通過有限域高斯消元方法求解出余數矩陣。

（2）密鑰分配中心將AES 密鑰分發給各節點，解出商矩陣。

（3）通過除法逆運算求解以及logistic 解密運算解出原始數據。

4 安全性分析

結論1 攻擊者在竊聽全部密文的情況下，竊聽者只能通過窮舉法來獲取信源消息。

證明：竊聽者了解整個網絡的編碼方案，通過竊聽信道獲得所傳輸的數據Data，通過解碼能得到余數矩陣Re，而商矩陣通過AES 加密進而不能夠獲取Z矩陣，所以只能通過窮舉的方法猜測矩陣Z的數值。

結論2 竊聽者通過窮舉法無法獲得序列Z，所以無法獲得信源消息X。

證明：已知ti是由yi的2,4,6,8,10 位組成的整數，tm 屬于[0，100000]，而ym 截取小數點后的12 位，范圍為[10^-12，0]，z的范圍在[0，10^17]。

通過計算得出t＞1，而進行網絡編碼信源節點的組播率m應大于1，且m，n均為整數，所以t一定大于1，能夠抵抗全局竊聽攻擊。

5 信源編碼方案舉例

下面以圖1 為網絡模型，給出一個在有限域F28的安全網絡編碼（數據用十進制表示）。選取兩信源節點組播率均為2，數據長度n均為1。以信源節點1 為例，x1={38,121}T。設定logistic 混沌系統初始值向量為：

經過公式（1）500 次迭代得到y={0.8634074378729123 0.6322734168356746},利用y向量，提取T矩陣，通過公式（3）計算得到Z：

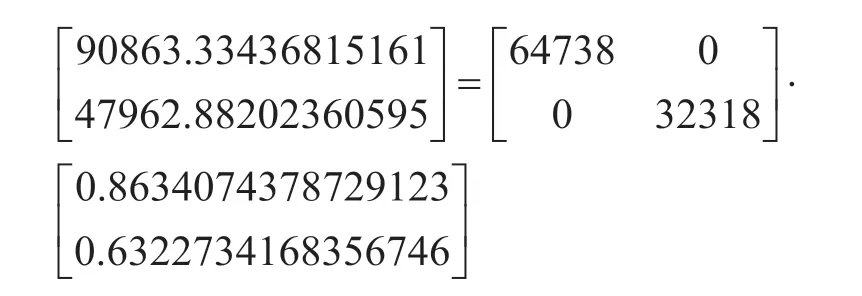
利用公式（4）計算攜帶信源節點1 原始消息的矩陣A：

對矩陣A進行整數運算，并對256 進行除法運算得到余數矩陣和商矩陣：

利用AES 加密算法對商矩陣進行加密，得到一維字節數組：

最后對余數矩陣進行網絡編碼，將系數矩陣、商矩陣加密后的字節數組以及網絡編碼的結果矩陣進行打包，向下傳輸。

6 性能分析

6.1 加密量

本文通過加密商矩陣部分防止竊聽者獲取明文信息，商矩陣大小為m*n，所以加密量為m*n。

6.2 通信開銷

本文的編碼方案不需要傳輸預編碼矩陣，傳輸過程除系數矩陣和編碼結果外需要添加編碼冗余為m。

6.3 信源編碼復雜度

在信源編碼過程中，需要進行除法操作，也需要對信源消息進行網絡編碼，所以編碼復雜度為O(m2n)。

6.4 組播率最小值

在結論二中可知，該方案對組播率沒有限制，所以信源組播率最小值為1。

6.5 使用場景

經過理論驗證，該方案對信源組播率沒有要求，各個信源編碼方案互不干涉，所以既適用于單源網絡編碼，也適用于多源網絡編碼。

7 結語

本文結合 Logistic 混沌序列提出一種抗全局竊聽的編碼方案，該編碼方案只需在信源節點處利用混沌序列產生大數隱藏信源消息，并通過AES 加密商矩陣便可有效對抗網絡竊聽。相比傳統方案，該方案沒有增加寬帶開銷。本文方案只考慮竊聽攻擊不能抵抗拜占庭攻擊，因此本文下一步研究方向為利用混沌加密對抗污染攻擊。