機載光電跟蹤系統的模糊控制算法研究
王曉迪,扈宏杰
(北京航空航天大學 自動化科學與電氣工程學院,北京100191)
光電跟蹤系統在軍事領域中有著非常廣泛的應用[1-2],但其結構中普遍采用的直流有刷電機的電刷與換向片之間存在機械摩擦,會產生金屬粉塵甚至“環火”,不適合在機載低氣壓的環境下工作。隨著光電跟蹤系統性能的不斷提高,直流有刷電機已難以滿足要求,而永磁同步電機(PMSM)輸出力矩平滑,且無需電刷換向,可靠性高,是替代直流有刷電機的理想選擇[3-4]。
現有光電跟蹤系統的跟蹤回路多采用傳統PD控制器進行控制,具有可靠性高、使用簡單方便等優點,但因參數較為固定,系統快速性和超調量間的矛盾難以調和,且跟蹤精度較差[5]。因此,本文設計了一種遺傳算法優化的跟蹤回路模糊PD 控制方案,根據脫靶量信息在線調整PD 控制器參數,從而使系統獲得更加優秀的動態性能。
1 光電跟蹤系統的控制原理
1.1 PMSM 的數學模型
采用矢量控制的方法[6],將定子電流矢量轉換為勵磁和轉矩電流分量,方程如下:

PMSM 的電磁轉矩方程為

式中:ψd、ψq為定子在d、q 軸上的磁鏈分量。
采用id=0 的控制策略,則式(3)可寫為

此時PMSM 等效為直流電機,可以控制q 軸電流以對電磁轉矩進行控制。
1.2 光電跟蹤系統的構成
采用跟蹤回路內置穩定回路的方式進行控制,結構如圖1 所示,穩定回路用來隔離干擾[7],而跟蹤回路通過圖像處理得到脫靶量,形成閉環控制,保證平臺能夠準確地保持在位置角度的指令值,是控制系統中保證平臺跟蹤性能最為關鍵的部分之一[8]。本文采用遺傳算法優化的模糊PD 控制器代替傳統PD 控制器實現對跟蹤回路的控制,以使系統獲得更加優良的性能。
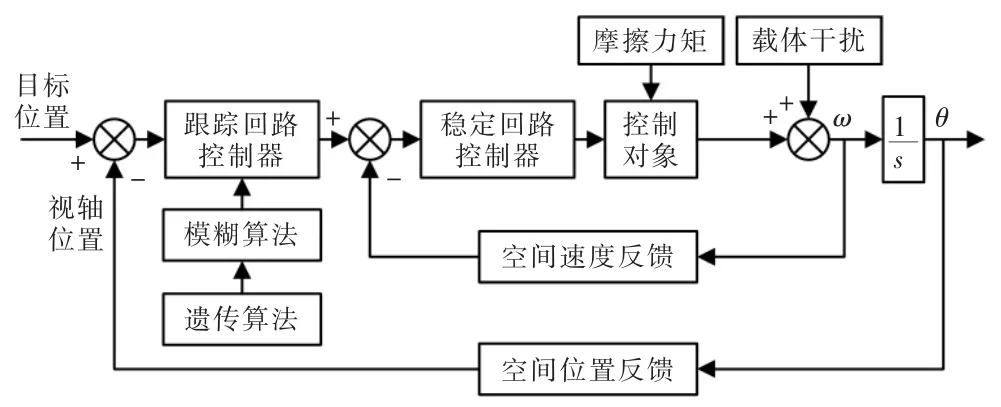
圖1 光電跟蹤系統的結構Fig.1 Structure of photoelectric tracking system
2 跟蹤回路控制器設計
2.1 模糊PD 控制器的結構
將模糊控制[9]與傳統的PD 控制器結合起來形成模糊PD 控制器, 選取實時的脫靶量e 和脫靶量變化率ec 作為兩個輸入變量, 通過模糊運算求得Kp、Kd的調整量ΔKp、ΔKd,利用式(5)在線整定PD控制器的參數。
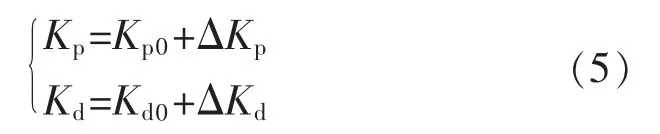
2.2 建立隸屬函數
采用合適的比例因子將變量的論域轉化到[-10,10],取模糊子集為{NL,NM,NS,ZO,PS,PM,PL},分別對應從“負大”到“正大”的語言變量。采用三角型隸屬函數,且邊緣設為Z 型,當位置偏差較小時,系統參數應有更加精細的劃分,故e 取非均勻隸屬函數,而ec、Kp、Kd的隸屬函數取均勻形式,分別如圖2 和圖3 所示。
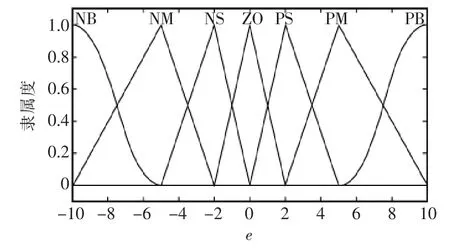
圖2 e 的隸屬函數Fig.2 Membership function of e
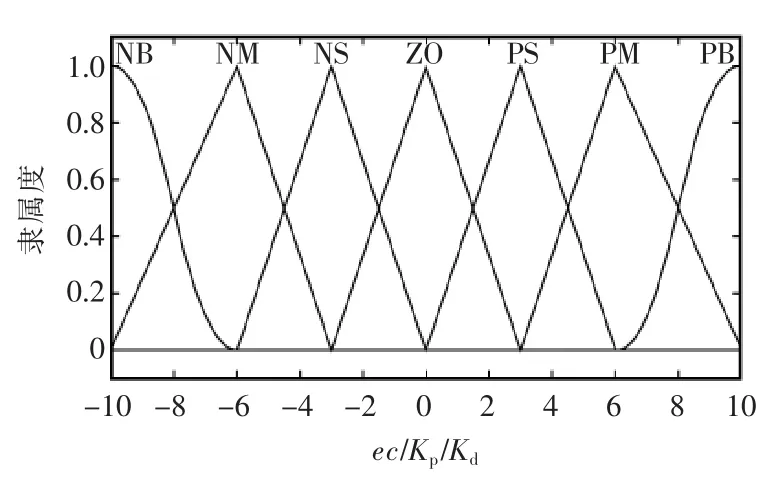
圖3 ec/Kp/Kd 的隸屬函數Fig.3 Membership function of ec/Kp/Kd
2.3 使用遺傳算法建立模糊控制規則
傳統的模糊控制規則通常依靠經驗建立,具有很大的盲目性,本文采用遺傳算法[10]進行尋優,并完成模糊控制規則的建立。設定種群數量為100,終止代數為40,每代精英個體數目為20,交叉概率0.8,變異概率0.001。綜合考慮跟蹤過程的快速性、超調量與精度,取性能指標為

式中:w1、w2、w3為權重;σ 為超調量;ts為系統調節至位置偏差滿足要求精度的時刻;ea為系統調節至位置偏差滿足要求精度后的絕對誤差平均值,其計算公式為

式中:T 為總時間。
為了便于實際計算處理,將性能指標做相應轉換,得到適應度函數:

式中:c 為靈敏度系數;k 為比例系數。
采用“IF…,Then…”的語句形式,經過遺傳運算后得到模糊規則如表1 和表2 所示。

表1 Kp 模糊控制規則表Tab.1 Fuzzy control rule of Kp
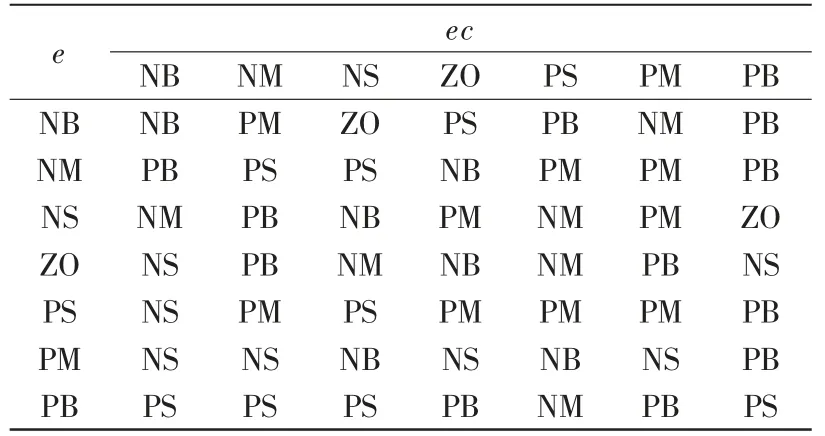
表2 Kd 模糊控制規則表Tab.2 Fuzzy control rule of Kd
2.4 模糊推理與解模糊化
建立模糊規則后,根據Mamdani 模糊系統的最大-最小法則進行推理, 并采用重心法解模糊化[11],其公式為

3 仿真與結果分析
電機基本參數如表3 所示,設定目標運動軌跡為x=1+0.1sin 2πt(°),載體擾動角速度為ωxd=ωyd=ωzd=sin(2πt)(°/s),設置控制器初始參數為Kp0=500、Kd0=0.5, 分別用傳統PD 控制器及本文建立的模糊PD 控制器對跟蹤回路進行控制,仿真結果見圖4 和圖5,可見使用模糊PD 控制器可以使系統擁有更小的超調、更快的調節過程和更高的跟蹤精度。

表3 電機各項參數Tab.3 Motor parameters
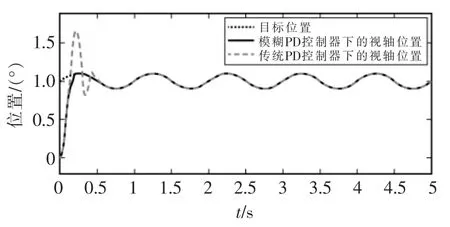
圖4 跟蹤過程中的目標位置與視軸位置Fig.4 Target position and boresight position during tracking
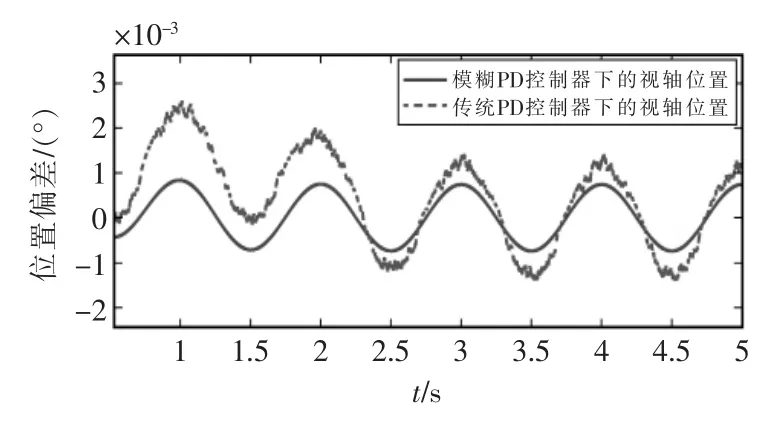
圖5 跟蹤過程中目標與視軸的位置偏差Fig.5 Position deviation of target and sight axis during tracking
圖6 和圖7 為模糊算法對Kp和Kd的整定過程, 可以得到整體規律: 位置偏差較大時,Kp和Kd都取較大值,以獲得更快的調節速度;位置偏差適中時,Kp和Kd變化較大,在保證系統響應快速性的基礎上防止產生較大超調; 位置偏差較小時,Kp取值很大,Kd取值較小,以提高跟蹤精度。
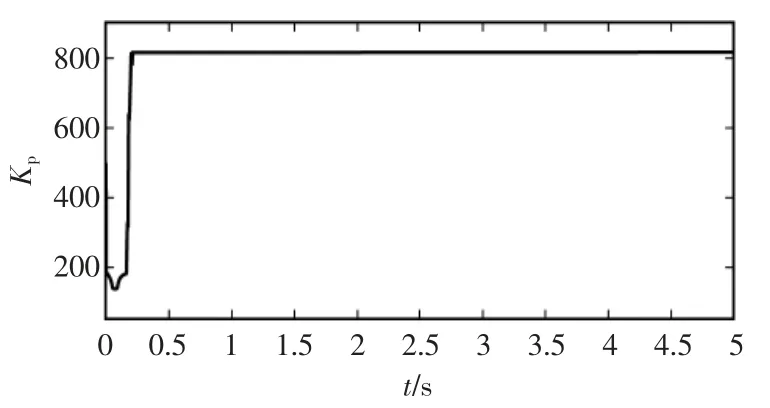
圖6 Kp 的整定過程Fig.6 Tuning process of Kp

圖7 Kd 的整定過程Fig.7 Tuning process of Kd
4 結語
本文采用PMSM 作為驅動,分析了光電跟蹤系統的控制結構,并建立了相應的仿真模型。針對傳統PD 控制在高精度光電跟蹤系統中存在超調量大、反應較慢、跟蹤誤差大的問題,設計了應用于跟蹤回路的模糊PD 控制器, 采用遺傳算法優化模糊控制規則,并提出了一種適用于光電跟蹤系統的適應度計算公式。仿真結果表明模糊PD 控制器的參數可以根據脫靶量和脫靶量變化率進行自整定,且模糊PD 控制器能夠基本消除超調, 實現快速高精度的響應,相比傳統PD 控制器有很大的優越性,具有很好的工程應用價值。

