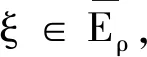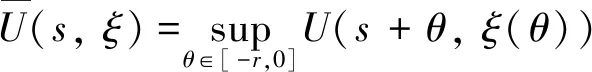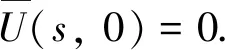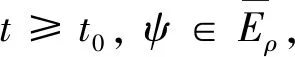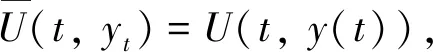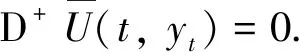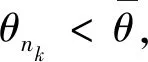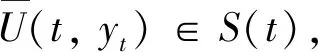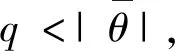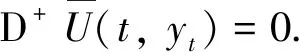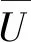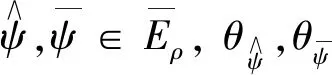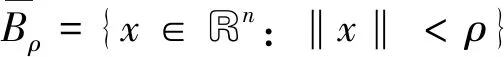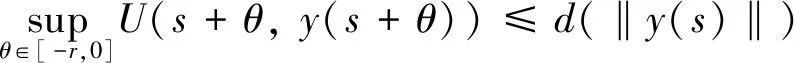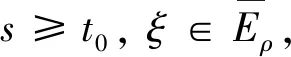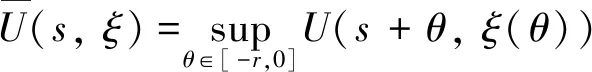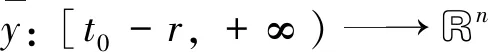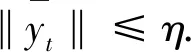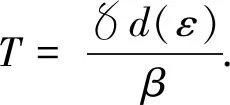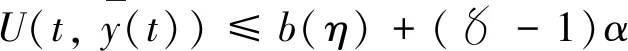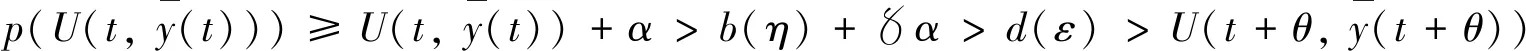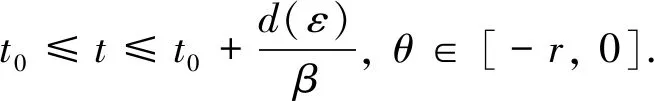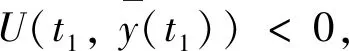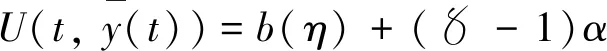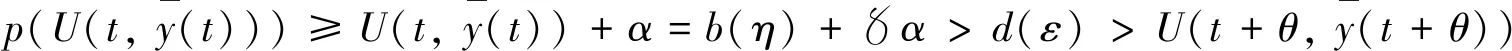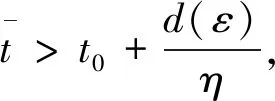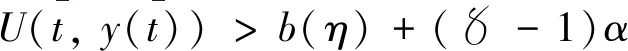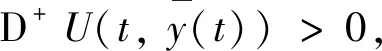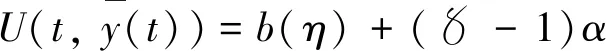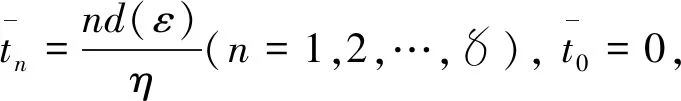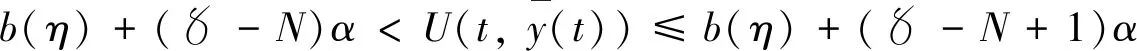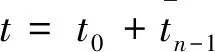測度中立型泛函微分方程的穩定性

李寶麟，席 婭

西北師范大學 數學與統計學院，蘭州 730070

我們考慮測度中立型泛函微分方程

D[N(xt，t)]=f(xt，t)Dg

(1)

的穩定性，其中D[N(xt，t)]和Dg(t)是N(xt，t)和g(t)的分布導數，xt(θ)=x(t+θ)，θ∈[-r，0]，t∈[t0，+∞)，且N是一個線性的非自治算子．測度微分方程已經被很多學者研究[1-4]．文獻[5]建立了測度泛函微分方程的Lyapunov定理．文獻[6]建立了測度微分方程和時間尺度上動力方程的Lyapunov穩定性．文獻[7-9]利用非單調Lyapunov泛函研究了滯后型方程的穩定性．文獻[10]在不利用Lyapunov泛函方法的情況下研究了多變時滯Volterra型動力系統的穩定性．文獻[11]利用Lyapunov泛函研究了一類潛伏期和傳染病期均傳染的SEIQR流行病模型的穩定性．文獻[12]通過Lyapunov泛函建立了非自治泛函微分方程的漸近穩定性定理．文獻[13]運用廣義常微分方程的變差穩定性和Lyapunov泛函建立了變差脈沖泛函微分方程的穩定性定理．

方程(1)的積分形式為

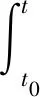
(2)

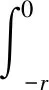
(3)

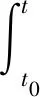
(4)

(4)式右邊的積分可以是Riemann-Stieltjes積分、Lebesgue-Stieltjes積分或Kurzweil-Henstock-Stieltjes積分[14]．

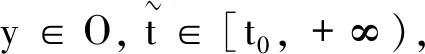
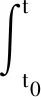
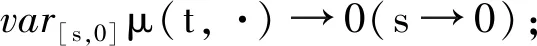
1 預備知識

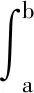
(5)

在區間[α，β]?[t0，+∞)上的解是指： 對每個γ，v∈[α，β]，(x(t)，t)∈Ω，t∈[α，β]，有

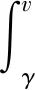
設集合O=Bc={x∈G-([t0-r，+∞)，Rn)： ‖x‖≤c，c>0}具有延拓性質，且

P={yt：y∈Bc，t∈[t0，+∞)}?G-([-r，0]，Rn)

引入概念[·，·，·]，其中對于a≤c，有： [a，b，c]=b，b∈[a，c]； [a，b，c]=a，b≤a； [a，b，c]=c，b≥c．對于每個y∈Bc，t∈[t0，+∞)，?∈[t0-r，+∞)，定義函數

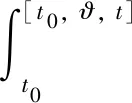
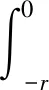
F(y，t)(?)=H(y，t)(?)+J(y，t)(?)

(6)

‖F(x，s2)-F(x，s1)‖≤|h(s2)-h(s1)|

及

‖F(x，s2)-F(x，s1)-F(y，s2)+F(y，s1)‖≤‖x-y‖∞|h(s2)-h(s1)|

(7)

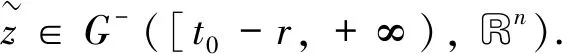
2 主要結果

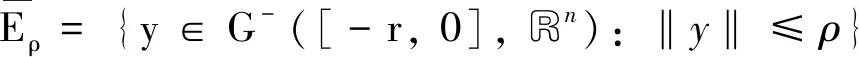
定義3設y≡0是測度中立型泛函微分方程(4)的平凡解，

(8)

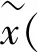
(9)

V(t，xψ(t))=U(t，yt(t，ψ))

(10)

則有

(11)

注1給定t≥t0，由

則有‖yt(t，ψ)‖=‖xψ(t)‖．

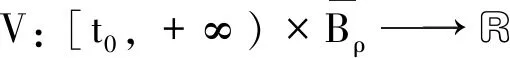
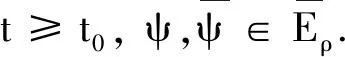
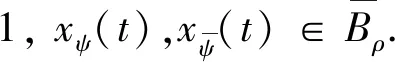
則由注1，有

(12)

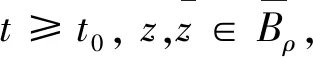
由注1，有

‖ψ‖=‖yt(t，ψ)‖=‖xψ(t)‖=‖z‖≤ρ

則測度中立型泛函微分方程(4)的平凡解y≡0是一致穩定的．

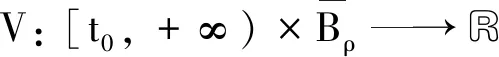
b(‖xψ(t)‖)=b(‖yt‖)≤U(t，yt(t，ψ))=V(t，xψ(t))

(13)

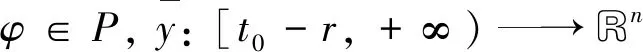
‖φ‖<δ

(14)

下面證明

(15)

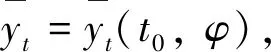
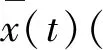
(16)

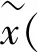
(17)

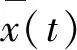
由(14)，(17)式，有

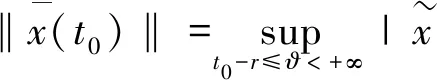
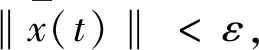
(18)

則(15)式成立，即測度中立型泛函微分方程(4)的平凡解y≡0是一致穩定的．

D+U(t，ψ)≤-Λ(‖ψ‖)t≥t0

(19)

則測度中立型泛函微分方程(4)的平凡解y≡0是一致漸近穩定的．

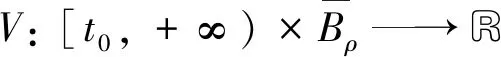
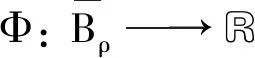
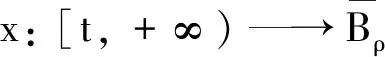
又由于‖yt‖=‖xψ(t)‖，則由注1，有

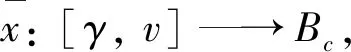
則

(20)

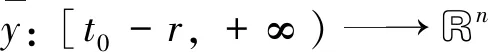
‖φ‖<δ0

(21)

下面證明

(22)

由(21)式，有

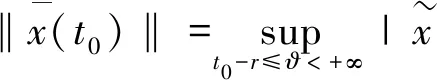
由(20)式，定理1證明中的(18)式成立，即(22)式成立．則測度中立型泛函微分方程(4)的平凡解y≡0是一致漸近穩定的．

其中y(s，t，ψ)是測度中立型泛函微分方程(4)的解，滿足yt=ψ，ψ∈G-([-r，0]，Rn)．給出一個初值函數ψ∈G-([-r，0]，Rn)且t≥t0，由文獻[14]的定理5.2，存在測度中立型泛函微分方程(4)的唯一解滿足yt=ψ，y(t)=ψ(0)，則D+U(t，y(t))可以改寫為D+U(t，ψ(0))．

存在，且滿足U(t-，y(t-))=U(t，y(t))，其中y∈G-([t0-r，+∞)，Rn)．假設U滿足以下條件：

|U(t，x)-U(t，y)|≤Ka‖x-y‖t∈[t0-r，+∞)，x，y∈Ba

其中Ba={z∈Rn： ‖z‖

則測度中立型泛函微分方程(4)的平凡解y≡0是一致穩定的．

(23)

(24)

考慮以下兩種情況：

U(t+θ，y(t+θ))

則對所有足夠小的q>0且q<|θ0|，有

或

及

或

另外，有

存在，且滿足U(t-，y(t-))=U(t，y(t))，其中y∈G-([t0-r，+∞)，Rn)．假設U滿足定理3中的條件，，，并且存在Hahn class函數d： R+R+，使得對測度中立型泛函微分方程(4)的每個解y，有

(25)

D+U(t，ψ(0))≤-Λ(|ψ(0)|)

(26)

則測度中立型泛函微分方程(4)的平凡解y≡0是一致漸近穩定的．

(27)

則由定理3的證明，方程(4)的平凡解y≡0是一致穩定的．

(28)

其中d是增函數．

首先，找出數T．由函數p(s)的性質，存在數α>0，使得對b(η)≤s≤d(ε)，有p(s)-s≥α(注意b(η)≤b(ε)≤d(ε))．設是正整數，使得b(η)+α>d(ε)，由于b(η)≤d(ε)，有d-(b(η))≤ε，設

假設

(29)

并且有

即

則由(26)式，有

則

運用前面的證明方法，有

及