丁字尺與角度配合法測量全站儀高度的方法

張根山，張利來，許東偉，王 俊

(1. 中國電建集團河北省電力勘測設計研究院有限公司，河北 石家莊 050031；2. 東北石油大學，黑龍江 大慶 163318)

0 引言

三角高程中間測量法[1-3]具有較廣的應用范圍，一般情況下可代替傳統的對向觀測法等，但在特殊地形條件下仍采用對向觀測法或單向觀測法效果更好。例如，兩個控制點之間為較寬的河流或較陡的山坡，進行對向觀測，一站可完成，而采用三角高程中間測量法則要繞行，不得不建立多個測站。又如，對于大跨徑懸索橋主纜線形測量[4]，待測目標在寬闊的水面上，三角高程需要進行單向觀測。可見，對向觀測法或單向觀測法三角高程測量在一些特殊地形條件下尚不能完全被其他方法所代替，仍有一定的使用意義。

對向觀測法或單向觀測法三角高程測量需要測量全站儀高度。楊黎明、王濤[5-8]等對比較精確測量全站儀高度做了一些有益嘗試。楊黎明[5]等對三腳架進行改造，研制了專用裝置。王濤[6]等 在對三腳架進行局部改動基礎上配對新設計的尺子，呂海波[7]等 提出了基于正余弦定理，借助萬能角度尺和鋼卷尺測量全站儀高度的方法。呂海波[8]等 提出了借助普通平面鏡和塔尺測量全站儀高度的方法。以上方法各有特點。

為了獲得比較精確的全站儀高度，本文提出了丁字尺與角度配合法。利用丁字尺尺頭與尺身相互垂直的特點，結合全站儀對中器激光束(或光學對中器十字絲)和垂直角，在幾何上構建一個直角三角形，根據三角函數關系算得儀器高度。此方法簡便實用，精度較高。

1 丁字尺檢測

1.1 檢測丁字尺垂直度

利用全站儀十字絲，檢測不銹鋼丁字尺垂直度。丁字尺是傳統的繪圖輔助工具，由尺頭和尺身構成，具有尺頭與尺身相互垂直的特點。為了減小外界因素引起的變形和保證測量精確性，這里采用不銹鋼制造的丁字尺。對于標準的丁字尺，首先測量尺身上緣和尺頭內側邊的垂直度，然后測定尺身長邊上緣實際長度，同時測定尺身上緣到尺頭下端的垂直距離。

為了敘述方便，記尺身長邊的上緣與尺頭的結合點為e，記尺身長邊上緣的另一端為f。同時，記尺頭上端中內側的端點為n，記尺頭下端中內側的端點為m。作為標準的丁字尺，當尺身長邊上緣ef處于水平狀態時，尺頭內側邊上的e、n、m三點處于垂直線上。這時，尺身長邊長度為fe，尺身上緣到尺頭下端垂直距離為me。

當尺頭內側邊與尺身長邊上緣未嚴格垂直時，以其尺身長邊為水平狀態，出現尺頭上端向尺身方向內傾或者外傾的情況。

尺頭內傾如圖1所示。對于尺頭內傾的情況，當尺身長邊上緣ef處于水平狀態時，使垂線過尺頭的下端中內側的端點m，然后與尺頭上端交于一點，記作n′，同時，延長尺身長邊上緣fe直線，與該垂線交于e′點。這時，尺身長邊長度為fe′，尺身上緣到尺頭下端的垂直距離為 me′。

尺頭外傾如圖2所示。對于尺頭外傾的情況，當尺身長邊上緣ef處于水平狀態時，使垂線過尺頭的上端中內側的端點n，然后與尺頭下端交于一點，記作m′，同時，延長長邊上緣fe直線，與該垂線交于e′點。這時，尺身長邊長度為fe′，尺身上緣到尺頭下端的垂直距離為m′e′。

丁字尺尺頭傾斜程度很小，為了表示清晰，圖上尺頭傾斜有所放大。

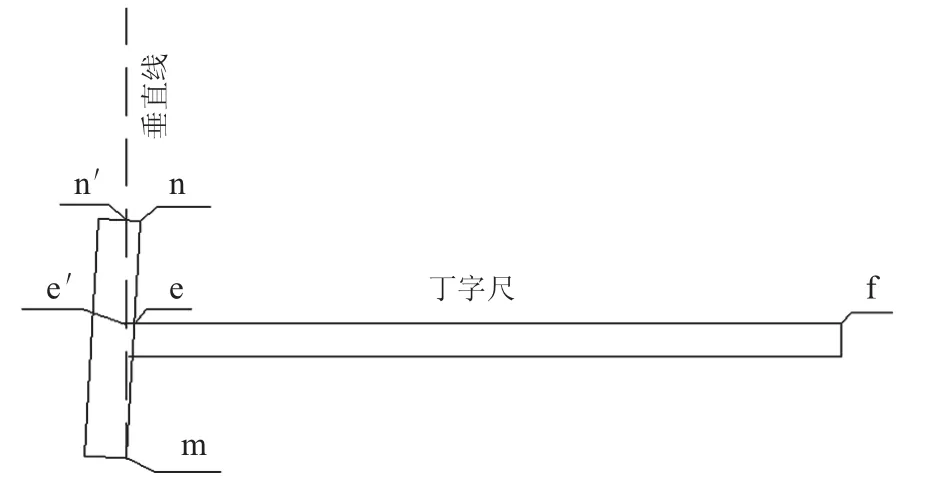
圖1 尺頭內傾圖

圖2 尺頭外傾圖

1.2 檢定尺身長邊上緣長度

使用年檢后的鋼尺檢測丁字尺長度。丁字尺放置水平，以鋼尺測量尺身長邊上緣長度，進行溫度改正，得到實際長度。

移動支付呈現的快速發展態勢取決于智能手機用戶數量、APP普及度及移動支付實際使用率等因素。［2］目前，移動支付正在大力發展線下業務，不斷豐富支付場景，如:公共交通，用戶可在地鐵站通過掃描二維碼購票，極大地提高了公共交通的售票效率，同時也為廣大消費者提供了更方便、快捷的用戶體驗。可見，移動支付市場的未來發展前景不可估量，這對于商業銀行來說具有極大的挑戰。

1.3 測定尺身上緣到尺頭下端的垂直距離

使用年檢后的鋼尺精確測定尺身上緣到尺頭下端的垂直距離。

2 丁字尺與角度配合法

把儀器精確對中和整平后，對中器激光束(或光學對中器的十字絲)與地面控制點形成一條垂直線。對于標準丁字尺，以其尺頭下端的內側端點對準控制點中心 (m、C兩點重合)，調整其尺頭上端的內側端點位置，使其處于對中器激光束(或光學對中器的十字絲)與地面控制點形成的垂直線上，這時，丁字尺尺身長邊上緣處于水平狀態。

這樣全站儀中心垂直線和丁字尺尺身長邊上緣作為兩個直角邊，加上垂直角對應的視線，就構成了一個直角三角形，如圖3所示。

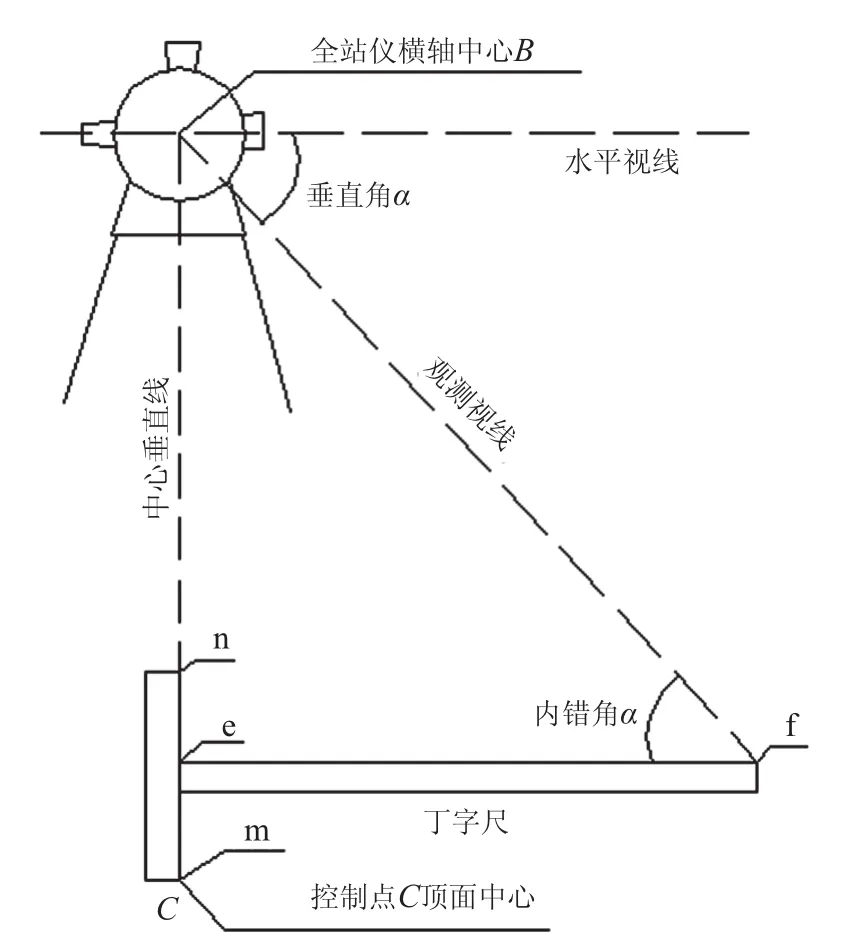
圖3 丁字尺與全站儀位置關系圖

根據尺身長邊上緣長度ef和對應的垂直角α，利用三角函數關系推算出全站儀上部高度Be，再加上尺身上緣到尺頭下端的距離em，可得全站儀整體高度BC。

測量垂直角一測回。如圖3所示，在標準丁字尺情況下則有下式成立

于是，全站儀高度

2.1 精度估算

2.1.1 精度估算公式

式(2)中ef、em、α的實際觀測值存在誤差，這些誤差按照一定形式導致函數BC的誤差。ef、em、α的誤差def、dem、dα是多元自變量，BC的誤差dBC為其函數，這里認為誤差def、dem、dα各自獨立，則得全微分如下式。

式中，ρ=206 265″。

測角精度可達±5″，而且ef距離不超過1.5 m，所以 ef×sec2αdα/ρ 項很小，即垂直角誤差影響可忽略。

由式(4)簡化得，

2.1.2 精密測距的誤差來源及其中誤差

由式(5)可見，全站儀高度中誤差與丁字尺測距中誤差密切相關。在本方法中丁字尺測距中誤差主要包括尺長檢定誤差、溫度改正誤差，還有對中器校正誤差等。

1.5 m鋼尺的首次檢定示值(I級)最大允許誤差值[9]為±0.40 mm。對于1.5 m鋼尺，在嚴格測量下，溫度改正誤差很小，可忽略。

對中器對中誤差對測距影響比較明顯。文獻[10] 對精密整平和對中技術進行了研究,認為光學對點器誤差優于±1 mm。檢定規程[11]要求光學對點器對中誤差不超過±1 mm。

取對中器對中誤差±1.0 mm和丁字尺測距中誤差±0.40 mm估算，則測距中誤差mS=±1.1 mm。

2.1.3 四等三角高程儀器測高允許中誤差估算

2.1.4 精度估算舉例

根據四等三角高程儀器測高允許中誤差的要求，mBC≤±1.58 mm。如果取mef=±1.1 mm，mem=±0.5 mm，結合(5)式得，tanα≤1.36，即只要儀器測高時垂直角α不大于53°，即可滿足四等三角高程要求。

2.2 望遠鏡最短視距的限制

不同型號全站儀的最短視距有所不同。一些型號全站儀最短視距為1.7 m，許多型號全站儀最短視距不大于1.5 m。觀測時要滿足最短視距要求。

3 效果驗證

測前，對水準儀和水準尺進行檢查，對i等進行了檢校。其中，i角=3.5″，符合DL/T 5001—2014《火力發電廠工程測量技術規程》中二等水準測量對DS05型水準儀的i角不得大于10″限差規定。

以1.2 m不銹鋼丁字尺配合徠卡TC1800全站儀，采用本法測出全站儀高度。同時，按照二等水準測量要求，視距在10 m之內，用DNA03水準儀測出全站儀橫軸中心到地面控制點之間的高差。12次二等水準高差和本法獲得高度對比結果如表1所示。

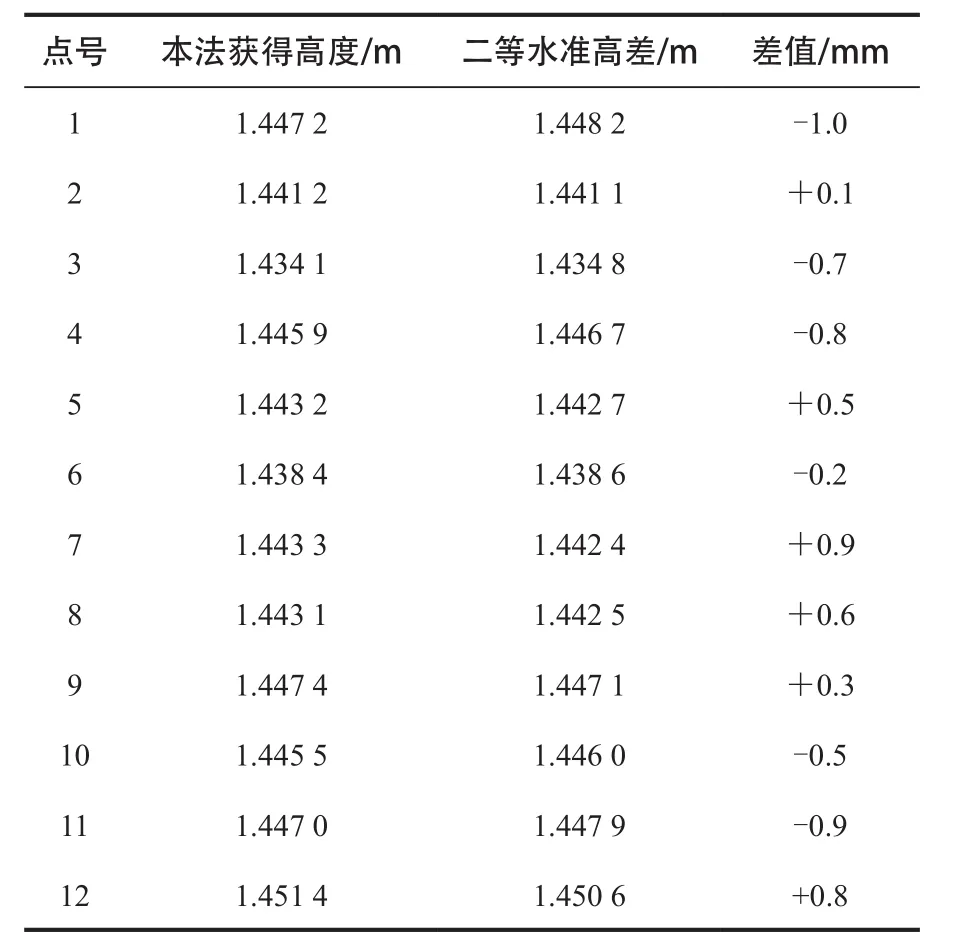
表1 本法與二等水準測量的高差對比

綜合表1數據，由于二等水準測量精度較高，當以二等水準高差為真值，對本法獲得的較少數據采取有偏估計，計算中誤差，得m=±0.7 mm。這說明在適當條件下本方法測量全站儀精度可以滿足四等三角高程要求。

4 三種方法特點比較

本文方法與王濤[6]、呂海波[7]方法進行了比較，結果如表2所示。

表2 三種方法特點比較表

從表2可見，王濤方法需要對三腳架進行改動、增加水準氣泡、設計專用尺子，測量精度較高；呂海波方法和本文方法都屬于間接測量法，不必對三腳架進行改動，也不用設計專用裝置，使用的都是一些常規測量工具，可以滿足相應三角高程精度需要；與呂海波方法相比，本文方法發揮了全站儀自身的更多功能，結果較精確。

5 結語

本文利用了全站儀垂直角功能和對中器的垂直線功能，結合不銹鋼丁字尺，在幾何上構建了一個直角三角形，根據三角函數關系推算出儀器高度。經過與二等水準測量對比，該法較精確，具有可行性。當地形條件受到限制，需要進行三角高程對向觀測或者單向觀測時，此方法可以簡便又比較精確地測量全站儀高度，對工程實踐有一定參考價值。