基于GAPSO-SVM 的滾動軸承故障分類方法

（浙江理工大學 信息學院，浙江 杭州 310018）

0 引言

現代社會機械設備構造復雜且生產環境多樣，在自動化程度高的生產線上一旦機器發生故障，將給生產作業帶來不同程度的損失。通用設備配有相當數量的滾動軸承。據統計，只有不到一成的軸承能夠正常運行到預期壽命年限，大多數軸承在使用年限內出現故障后，其造成的機器生產損失遠大于軸承自身價值。滾動軸承使用場景多樣，因此及時準確診斷軸承狀況可減少生產損失，相關研究具有十分重要的意義。

機器故障診斷技術主要分兩個階段：第一個階段以傳感器和信號技術為基礎，以信號處理作為手段進行故障診斷；第二個階段以機器學習算法為代表進行人工智能診斷［1］。對于滾動軸承故障診斷，主要利用以支持向量機（Support Vector Machine，SVM）為代表的人工智能領域算法。支持向量機是基于統計學的分類方法［2］，通過使用不同方法尋找多維超平面實現多維非線性數據分類和預測任務，此外支持向量機因易操作、自學習和比較強的泛化能力等特點，在機械故障診斷方面的應用較多，也積累了豐富的研究成果［3-5］。支持向量機分類效果很大程度上取決于參數選擇（如懲罰參數C 和核函數參數G）［6］，故一些學者通過智能搜索算法尋優支持向量機參數。方清等［7］提出粒子群（Particle Swarm Optimization，PSO）改進支持向量機算法，進行數據分類和趨勢預測，針對滾動軸承故障的分類實驗取得了良好效果；胡勤等［8］通過遺傳算法（Geneti?cAlgorithm，GA）改進支持向量機算法進行滾動軸承的故障診斷，較SVM 耗時短且精度高。但遺傳算法在解決規模計算問題時容易陷入早熟和搜索效率低的問題，粒子群算法容易陷入局部最優、過早收斂從而無法尋到全局最優解［9-11］。

本文利用基于PSO 算法與遺傳算法GA 的混合算法GAPSO 搜尋SVM 最優參數，利用改進算法對實驗數據進行測試，并將測試結果分別與GA-SVM、PSO-SVM 進行比較。實驗結果表明，GAPSO-SVM 算法可提高滾動軸承故障分類模型準確率，評價結果更優。

1 GAPSO-SVM 算法相關理論

1.1 SVM

SVM 是監督學習中最有影響力的方法之一。其基本模型是定義在空間上最大間隔的線性分類器，由于其遵循經驗風險與置信風險之和最小化（即結構風險）原理，因此SVM 泛化能力強。SVM 學習策略是使間隔最大化，對于已知數據集：T=｛（x1，y1），（x2，y2），……（xn，yn）｝其中，xi屬于Rn，yi屬于｛+1，-1｝，i=1，2，…N，xi為第i個特征向量，yi為類標記。如若yi＞0，則xi屬于正類，若yi＜0，則xi屬于負類。可形式化為凸二次規劃問題：

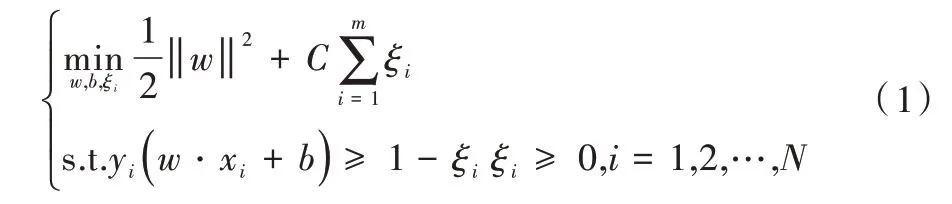
其中，ξ為松弛變量，w為超平面權系數向量，b是偏移量，C 是懲罰參數。引入拉格朗日乘子法，得到最優分類決策函數。

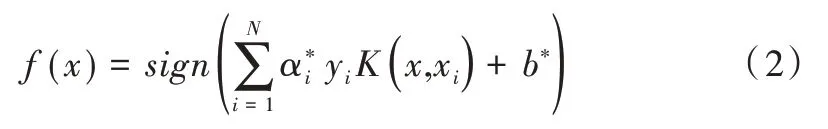
本文取徑向基核函數為：

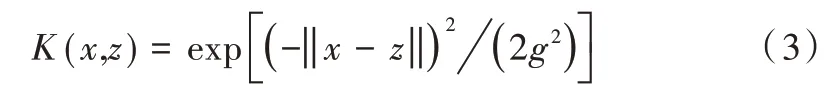
其中ai為拉格朗日乘子，K（x，xi）本文取徑向基核函數，式（3）中g 為核函數參數。核函數參數g 的取值對樣本劃分精細程度有重要影響，g 越小，低維空間中選擇的曲線越復雜，容易出現過擬合；反之分類結果粒度越粗從而欠擬合。懲罰因子C 的取值綜合考慮了經驗風險與結構風險，C 越大，經驗風險越小，結構風險越大，容易出現過擬合；C 越小，經驗風險越大結構風險越小。從而出現欠擬合。由此可見，懲罰因子C 與核函數參數g 的取值對支持向量機的結果精度有著至關重要的作用。

1.2 粒子群算法與遺傳算法

粒子群算法源于模擬鳥群捕食行為的過程，對1 個粒子種群而言，所有粒子可根據群體中對環境適應度最佳的個體位置調整自己位置，每個個體在搜索最佳適應度值時均可看作一個D 維空間中沒有體積的微粒，通過個體和同伴的飛行經驗調整自身飛行速度。第i個微粒表示為xi=（xi1，xi2，…，xid），其經歷的最好的適應值記錄為Pd=（p1d，p2d，…，pnd），也稱為pbest。群體所有經歷過的最好位置索引用符號g表示，即Pg，也稱為gbest。微粒i速度用Vi=（vi1，vi2，…，viD）表示。對每一代，它的第d+1 維（1≤d+1≤D）根據方程（4）、（5）進行變化。

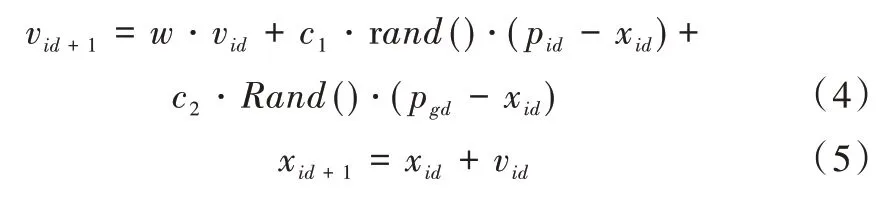
其中，w為慣性權重（inertia weight），c1、c2為加速常數（acceleration constants），rand（）和Rand（）為兩個在［0，1］范圍變化里的隨機值。

遺傳算法是借鑒生物進化規律演化而來的隨機搜索方法，無需導數或其它輔助信息，直接尋求最優適應度。遺傳算法的選擇、交叉、變異操作可按照概率化方法確定搜索空間和搜索方向，從而確定全局最優個體。

粒子群算法在搜索時容易陷入局部最優從而過早收斂，對處理多峰搜索任務時效果欠佳。遺傳算法搜索能力較強，當設置交叉參數較大時可產生足夠多的新個體從而增強全局搜索能力，因此本文提出利用遺傳算法改進粒子群算法。GAPSO 算法根據待優化參數的個數生成對應維度的粒子并進行模型訓練，在達到迭代次數時最佳適應度對應的粒子各維度參數即為尋優的最佳參數。算法流程包含8 個步驟：①確定目標函數。本文目標函數為SVM 的分類結果；②種群初始化。將C、G 初始化值作為粒子個體兩個維度；③參數初始化。根據經驗確定算法相關參數，包括粒子種群規模、每個維度上下界、迭代次數、交叉和變異概率；④適應度計算。本文以支持向量機的的交叉驗證準確率作為適應度；⑤確定最優解。根據最佳適應度大小，分別確定粒子群群體最佳極值與個體極值及遺傳算法全局極值并進行比較；最后得到GAPSO 全局極值，判斷全局極值是否滿足條件或已到達迭代次數，若是則輸出全局最優解，否則繼續更新迭代；⑥種群更新。更新遺傳算法全局極值及粒子群算法全局和個體極值。根據改進的選擇方法選擇種群，對種群進行交叉和變異操作，產生新的粒子。新粒子更新位置和速度，并按概率進行變異操作；⑦輸出全局最優解。得到全局最優的C、G；⑧將輸出的結果作為支持向量機的初始參數。

從圖1 中可以看出，相比PSO 算法，GAPSO 引入遺傳算法思想中的變異和雜交思想，一定程度上拓寬了粒子搜索空間，使粒子能在更大搜索空間搜索。遺傳算法改進的粒子群算法按給定的概率參數進行交叉和變異，在保持種群多樣性的同時擴大了搜索范圍、提高了搜索到最優值的幾率，擁有更廣泛的搜索能力。

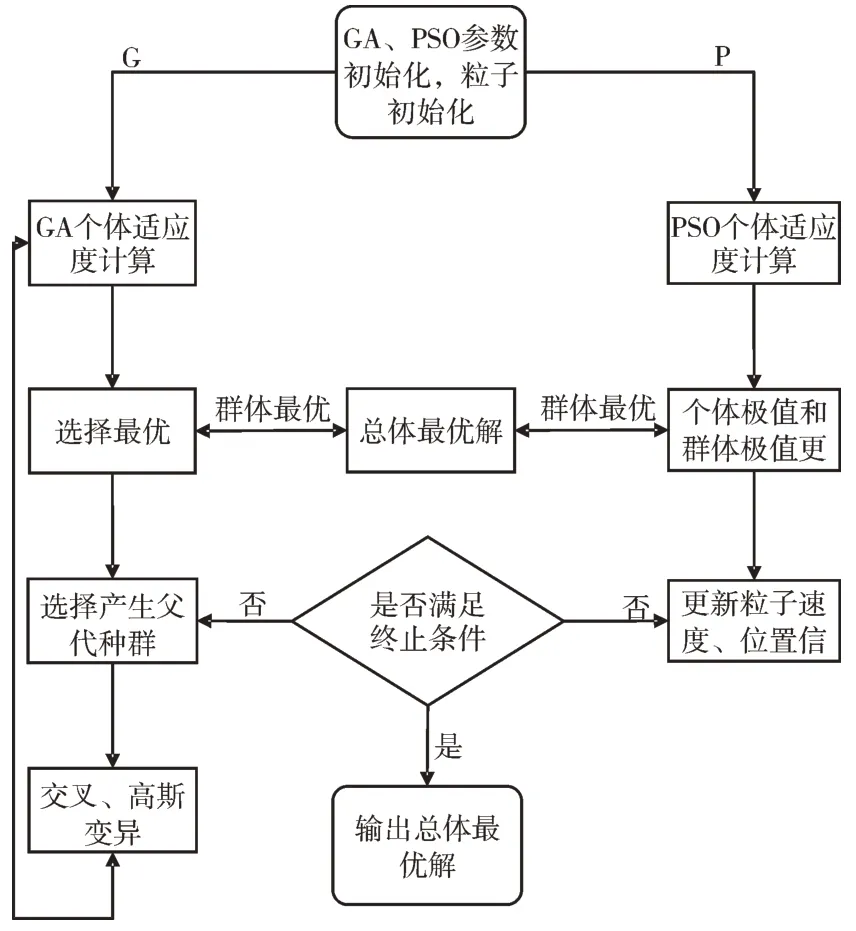
Fig.1 GAPSO algorithm flow圖1 GAPSO 算法流程

2 算法驗證

為驗證算法可行性和可靠性，本文從UCI 數據庫中取Wine、Iris、Heart 3 個數據集進行GAPSO-SVM 算法驗證與對比，算法平臺采用MATLAB2017a 軟件，實驗環境為Windows10 操作系統，Intel 3.1Ghz 處理器，從Libsvm 軟件庫選擇徑向基核函數工具箱。其中Wine 數據集來自意大利葡萄酒含量數據，包含蘋果酸、酚類、酮類和色調等13個維度特征，共3 個分類標簽；Iris 則是3 種鳶尾花數據集，共150 組數據包含萼片和花瓣長寬四維特征；Heart 數據集主要從易導致心臟病的13 個特征維度區分有無心臟病。3 種數據集劃分如表1 所示。

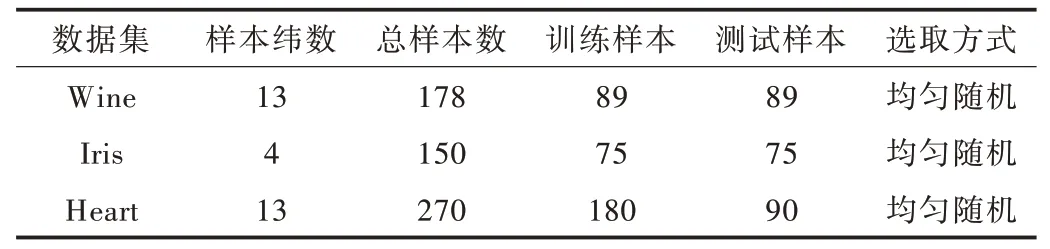
Table 1 Three kinds of data set sample division situation表1 3 種數據集樣本劃分

其中SVM 參數中懲罰因子C 取值范圍［0.1，100］，核函數參數g 取值范圍為［0.01，1000］，在GAPSO-SVM、GASVM 和PSO-SVM 算法中粒子群均為20 組，進化迭代次數為100 次。GAPSO-SVM 和PSO-SVM 學習因子C1和C2分別取1.5 和1.7，彈性系數為1，慣性權重取值［0.1，1.0］，GAPSO-SVM 中變異概率pm 取0.05，交叉概率取pc=0.5。利用這3 種分類器對這3 種數據集進行分類。分類結果如表2 所示。

由表2 看出GAPSO-SVM 在較低迭代次數時達到全局最優，在Wine 中雖代次數花費較高，但準確率提高5.3%，在另外兩個模型中，本文算法可快速找到全局最優，在相對錯誤率高的Heart 數據集中以85.56% 的準確率進行分類任務，由此可見，該算法在分類任務中可行可靠。

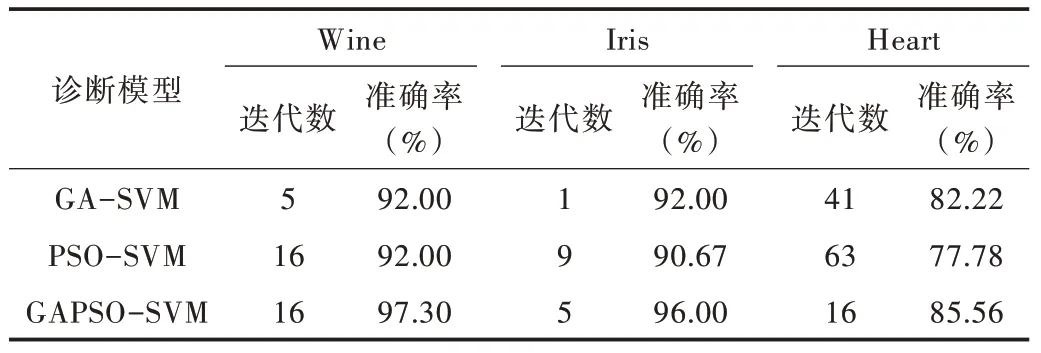
Table 2 Classification results of the three diagnostic models on the data set表2 3 種診斷模型對數據集的分類結果

3 實驗部分

3.1 數據來源與預處理

本文研究數據來自浙江紹興某軸承廠試驗臺采集信號，采集用傳感器為PCB PIEZOTRONICS，型號48OB，其中采樣頻率為10 240Hz，采集卡為CBOOK2000 高精度數據采集器。盡可能控制不同故障的外部環境，因此外部因素忽略不計。滾動軸承按正常和不同故障類型分為5 類：正常、保持架故障、滾動體故障、內圈故障、外圈故障。不同故障振動數據樣本見圖2。

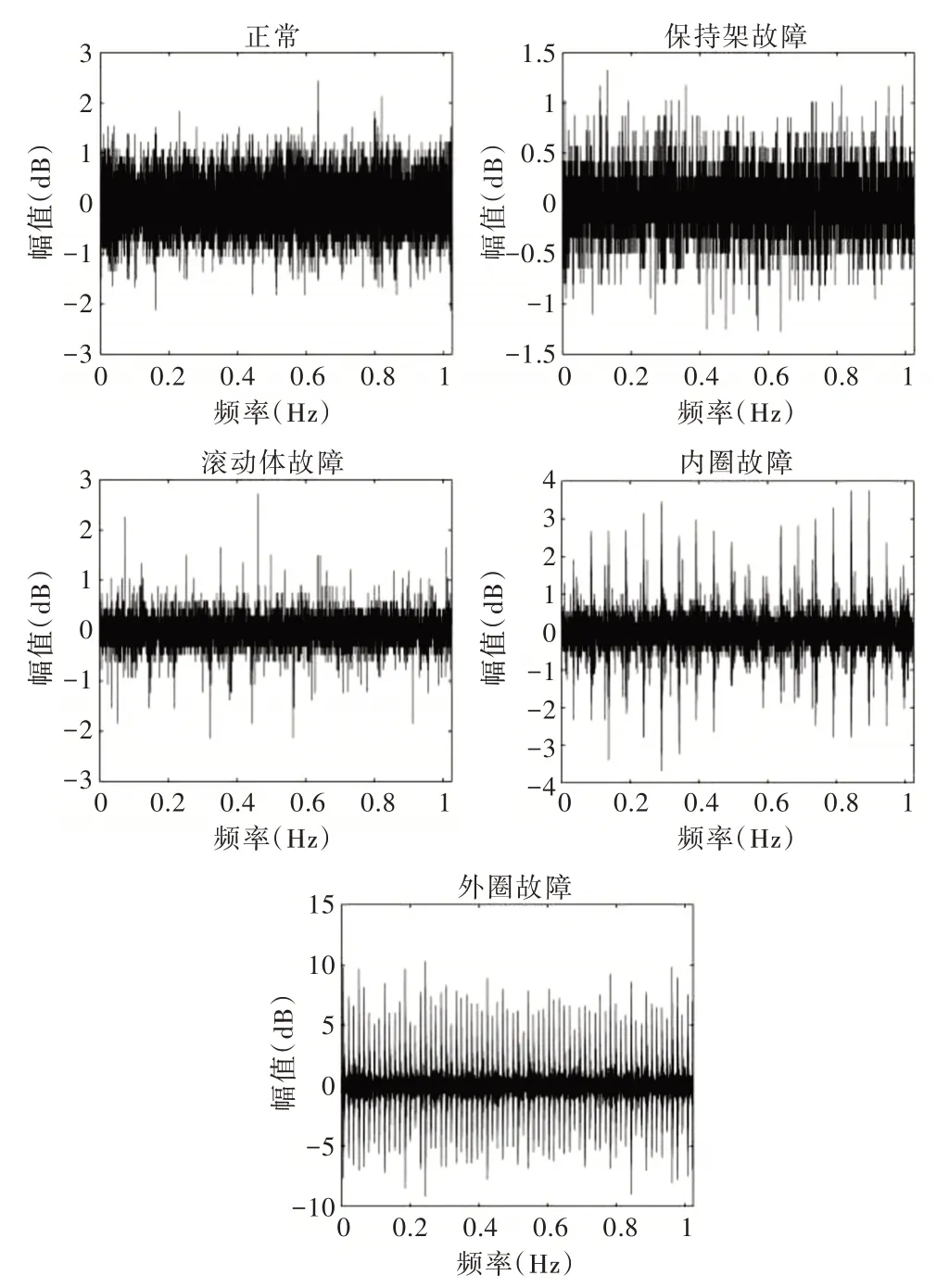
Fig.2 Time-domain waveforms under different faults of rolling bearings圖2 滾動軸承不同故障下的時域波形

滾動軸承發生異常時通常會導致振動信號時頻域特征參數發生變化［12-14］。本文首先對信號進行小波降噪，然后提取時頻域特征，其中7 個時域特征為：有效值、峰峰值、峰值指標、波形指標、脈沖指標、裕度指標、峭度指標［15］，如表3 所示。

振動頻譜通常在不同運行狀態下有很大差別，故通過頻譜分析亦可判斷滾動軸承故障類型。根據傅里葉技術理論，假設離散化后的振動信號時間序列為x（n），采樣頻率為fs，采樣點數為N，頻譜為s（k），k=1，2，…k，k 為譜線數。本文采用6 個頻域指標，如表4 所示。

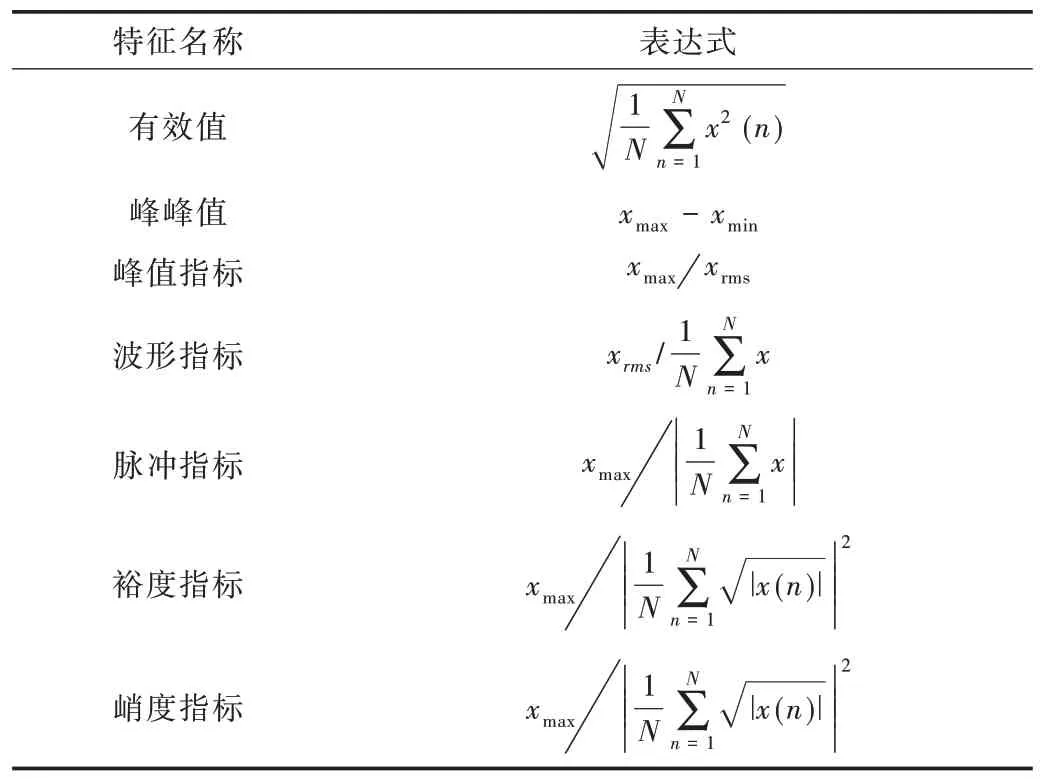
Table 3 Time domain feature samples表3 時域特征樣本

Table 4 Frequency domain feature samples表4 頻域特征樣本

表4 中F1表示振動能量大小；F2反映信號頻譜與信號頻譜均值的偏離程度；F3反映信號頻譜相對均值不對應程度；F4反映了信號在均值處峰值大小；F5反映了信號主頻帶位置的變化；F6反映了頻譜集中或分散程度。將經過小波降噪的振動數據提取時頻域后進行歸一化到［0，1］之間并喂入SVM 進行訓練。

3.2 實驗結果分析

本實驗特征集共分為時域、頻域、時頻域特征，各特征集取正常和4 種不同的故障狀態數據，各24 組共120 組訓練模型。其中設置GAPSOSVM 中參數搜索范圍c（0.1，100），g（0.01，1 000），種群規模為20，迭代次數為100，雜交概率為0.5，變異概率取0.05，最佳適應度采用SVM 最大交叉驗證正確率，其中GAPSO-SVM 對時頻域特征集的適應度曲線如圖3 所示。

由圖3 可知GAPSO 為SVM 尋優的最佳參數cbest=38.07，gbest=0.18。其中最佳適應度在最初幾代時陷入局部最優，但在接近迭代第42 次時跳出局部最優尋找到全局最優，準確率也達到98.75%。分類和預測數據取每種狀態8 組數據共40 數據。測試結果如圖4 所示。

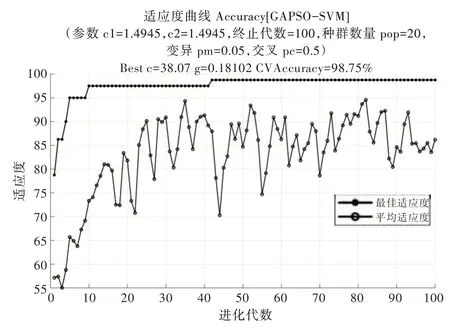
Fig.3 GAPSO-SVM best fitness curve圖3 GAPSO-SVM 最佳適應度曲線

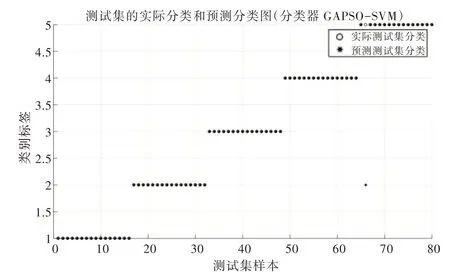
Fig.4 GAPSOSVM test set prediction accuracy圖4 GAPSOSVM 測試集預測精度

測試樣本按每種故障和正常各取8 組，本文分別采用PSO-SVM、GA-SVM 對相同訓練數據集和測試集進行效果對比。結果如表5 所示。時頻域集對應的3 種算法適應度如圖5 所示。

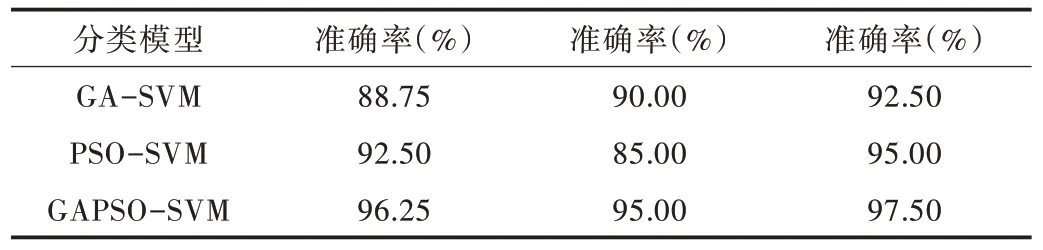
Table 5 Comparison of classifier efficiencywith different features表5 不同特征下的分類器效率對比

由表5 可看出GAPSO-SVM 明顯優于GA-SVM 和PSO-SVM 分類器。在時域和頻域單一特征集中，GAPSOSVM 分類精度達到96.26% 和95.00%，而在時頻域特征集中，精度高達97.50%，在40 個樣本中只有1 個樣本分類預測錯誤。圖5 中最佳適應度值的搜索曲線可以看出PSOSVM 在迭代不到10 次時即陷入局部最優，GA-SVM 在迭代接近40 次時，最優值產生變異，跳到適應度較小的值后又找到局部最優，而GAPSO-SVM 則在迭代次數不超過20次時找到全局最優。由此可見結合了遺傳思想和粒子群思想的分類器在滾動軸承故障分類中效果較好。在實時工業作業中，故障預測精度提升可在工業生產中減少損失并提高生產效率，而本文分類算法能以較少迭代次數尋找到最優模型，具有可觀的工業實際應用價值。

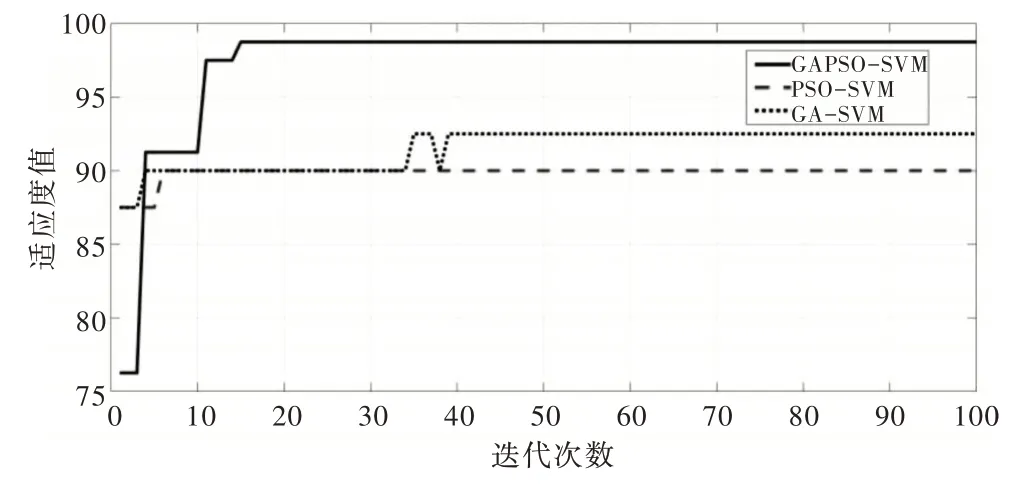
Fig.5 Fitness curves of three optimization algorithms圖5 3 種優化算法的適應度曲線

4 結語

本文結合遺傳算法和粒子群算法特點，提出GAPSOSVM 算法以實現全局搜索與局部搜索平衡。通過雜交變異部分粒子一定程度上提高了粒子群跳出局部最優的可能性，同時本文算法通過靈活控制雜交和變異概率、擴大粒子個數，可在復雜的分類任務中取得不錯的效果。

GAPSO-SVM 利用SVM 自學習、易操作、泛化能力強等特點，在小樣本、非線性問題上具有深度學習不可取代的優勢，且沒有過學習和欠學習的問題，應用場景廣泛。

利用提取后的特征集進行分類時，時域或頻域分類較時頻域集精度較低，通常需結合多個特征集進行模型訓練。本文通過時域、頻域及時頻域3 個數據集進行訓練，得出時頻域特征集表現最接近真實值。因此如何有效選用最具有代表的特征值進行分類任務是值得探討的內容。