基于時間序列和GRU的滑坡位移預測

鄢 好，陳 驕 銳，李 紹 紅，吳 禮 舟

(成都理工大學 地質災害防治與地質環境保護國家重點實驗室，四川 成都 610059)

1 研究背景

滑坡是一種危害極大的地質災害，滑坡的發生往往造成公路阻斷、供電供水設施毀壞、生態破壞，給人民群眾生命財產安全造成極大威脅。滑坡位移預測是滑坡災害防治的基礎性工作之一[1]。

數學模型預測是當前滑坡位移預測采用的主要方法。通常來說，滑坡預測方法可分為單因素和多因素預測法。例如Verhulst模型[2-5]、GM(n，1)[6-8]等單因素法運用于滑坡預測都取得了較好效果。隨著信息技術和監測技術的更新，目前更傾向于使用多因素法。杜鵑[9]等基于誘發因素的響應分析，搭建BP神經網絡對滑坡位移周期項進行預測；張俊[10]等基于時間序列與PSO-SVR耦合模型，建立了周期性位移與外在因素的響應關系；周超等[11]基于小波變換和ELM模型，提出了混沌時間序列WA-ELM 滑坡位移預測模型。一般認為，當信息足夠時，考慮多因素的“學習型”方法比考慮單因素的方法顯得更合理。但目前這類方法多屬于靜態模型[12]，限于隱含層網絡單向傳遞結構特點，往往無法顧及滑坡自身演化的趨勢，從而制約了模型的預測效果。隨著深度學習的興起，楊背背等[12]將長短時記憶網絡應用于滑坡預測，建立了滑坡位移變化過程的動態預測模型。GRU( Gated Recurrent Unit )作為長短時記憶網絡的一種優化模型，在自動化識別與分類方面取得了良好的效果[13-14]，但目前在滑坡位移預測中的應用研究還相對較少。

綜上所述，本文以三峽庫區八字門滑坡ZG111監測點為例，依據季節性降雨與庫水位變化導致滑坡的“階躍性”特征，建立時間序列模型，將位移分解為趨勢項和周期項。用灰色Verhulst模型預測趨勢項，基于誘發因素建立GRU模型預測周期項，并且與傳統的神經網絡GRNN(Generalized Regression Neural Network)模型進行對比分析，以均方根誤差RMSE和擬合優度R2評價各模型的預測精度，疊加趨勢項與周期項得到累計位移預測。

2 位移分解與預測方法介紹

2.1 基于時間序列的位移分解

山體滑坡位移的產生多是由內在因素(邊坡土體的性質、巖體結構、地質構造、地應力等)和外部因素(降雨、地表水和地下水的作用、地震以及工程荷載等)共同引起的[15-17]。對于八字門滑坡，內在因素是其固有變化特性，而外在因素為季節性降雨和庫水位周期性變化。據此，可將滑坡總位移進行如下分解：

x(t)=p(t)+q(t)

(1)

式中：x(t)表示總位移時間序列，p(t)表示位移的趨勢性部分；q(t)表示位移的周期性部分，該項位移是多種外部因素耦合的結果。

2.2 灰色Verhulst模型預測趨勢項

灰色Verhulst模型建立的過程與GM(1，1)類似，根據原始數據序列x(0)得到一階累加(1-AGO)新數據序列x(1)以及緊鄰均值生成序列z(1)，然后建立灰色Verhulst模型的白化微分方程：

(2)

式中：a，b為參數，由最小二乘法計算為

(3)

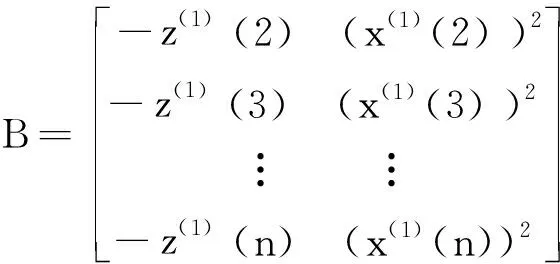
(4)

求解微分方程(2)可得模型的時間響應式：

(5)

對式(5)作累減還原，得到原始序列的灰色Verhulst預測模型為

(6)

2.3 基于深度學習方法預測周期項

傳統人工神經網絡ANN屬前向神經網絡，一個節點輸出值只能傳遞給下一層網絡的節點，同層之間的節點相互獨立。而在遞歸神經網絡RNN中，一個節點的輸出值理論上可傳遞給任意節點，作為該節點的輸入，在任一時刻的計算中，網絡不僅受該時刻輸入數據的影響，還受網絡歷史值的影響。基于對歷史信息的記憶特性，RNN與傳統ANN神經網絡相比(見圖1)，在處理時間序列問題上凸顯一定的優勢。

盡管RNN能夠有效處理非線性時間序列問題，但實際應用中，對于距離較遠的歷史信息，RNN學習能力會大大減弱[18-19]。基于以上問題，Hochreiter等提出了LSTM，結構如圖2(a)所示，在RNN的基礎上增加了輸入門(input gate)、遺忘門(forget gate)及輸出門(output gate)等記憶單元，大大提升了RNN的長時序處理能力。但LSTM模型結構過于復雜，故Cho在2014年對LSTM模型進行了優化，提出了GRU模型，包括將輸入門，遺忘門、輸出門變為更新門(update gate)和重置門(reset gate)以及將單元狀態ct和ht并為一個狀態ht。

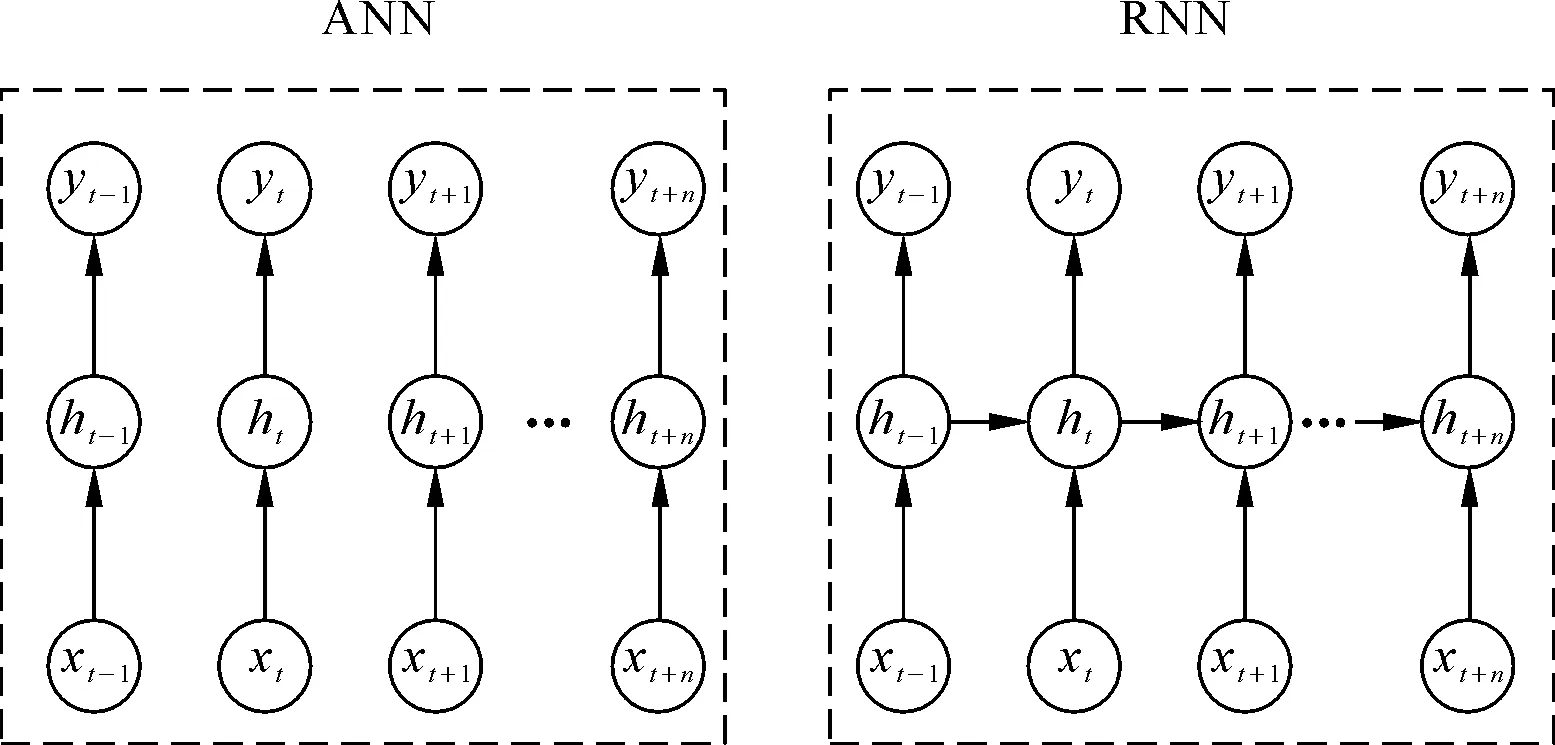
圖1 ANN與RNN對比示意Fig.1 Difference between ANN and RNN

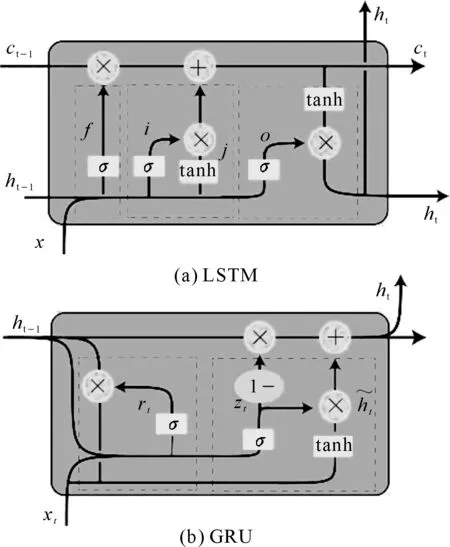
圖2 LSTM與GRU對比示意Fig.2 Difference between LSTM and GRU

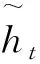
rt=σ(wr[ht-1，xt])

(7)

zt=σ(wz[ht-1，xt])

(8)

(9)

(10)

yt=σ(woht)

(11)

式中：wr為重置門的權重；wz為更新門的權重；tanh表示雙曲正切函數；σ為sigmoid函數。其中wz，wr，wh和w0為需要訓練的參數，其中前3個需要學習的參數是拼接而來：

wr=wrx+wrh

(12)

wz=wzx+wzh

(13)

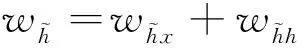
(14)

2.4 模型精度評價

預測模型的精度代表著預測值的可信度，擬合優度R2與均方根誤差RMSE用來評價模型的預測效果。此外，應用相對誤差和絕對誤差評價具體月份的預測效果，其中擬合優度和均方根誤差的計算式如下：

(15)

(16)

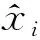
3 八字門滑坡變形概況

如圖3所示，八字門滑坡位于長江北岸支流香溪河右岸，距三峽大壩38 km。地勢西高東低，山前斜坡坡度約5°～30°，斜坡后部山體較陡，坡度約為42°～60°，滑體體積約為200萬m3，滑體高程分布為100～250 m，其中最大橫向寬度介于100～350 m。該滑體主要由破碎角礫巖和松散沉積物組成，現已存在兩個滑面：下部的主滑帶位于10～35 m的沉積物與基巖交界處；上部的次級滑帶是沿著早期滑面滑動形成，位于滑體中上部6～8 m和底部27～33 m處[20-22]。

八字門滑坡共設置ZG110、ZG111、GSC1、GSC2等10個GPS監測點，其中ZG110，ZG111于2003年開始監測，其余的從2013年9月開始監測。本文收集到的2004年1月到2012年9月的八字門滑坡監測資料如圖4所示[23]。

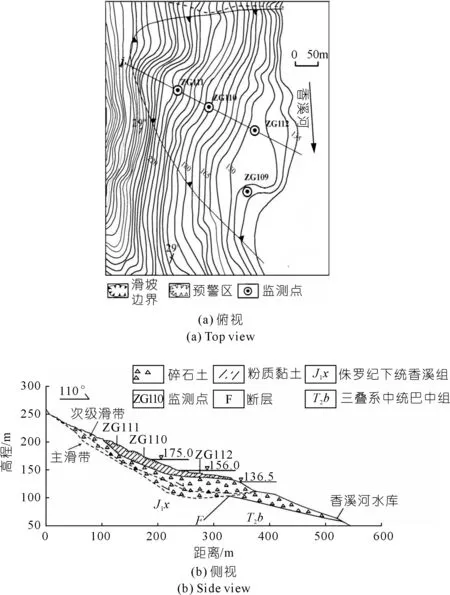
圖3 八字門滑坡地形Fig.3 Topographic map of Bazimen landslide

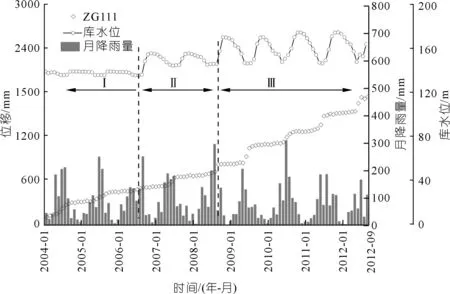
圖4 滑坡位移值和月降雨量Fig.4 Landslide displacement and monthly rainfall

每年的6～8月份，八字門滑坡的位移曲線呈階梯狀遞增，在地表形成大量的裂隙，如圖5所示，這些地表裂縫給當地居民生活帶來了嚴重的困擾[24-25]。這一時間段，三峽庫水位下降，雨量增加，位移出現明顯的“階躍性”增加，而在其他時間段，滑坡變形緩慢。根據庫水位和降雨的變化規律，滑坡累計位移時程曲線可分為3個階段。

(1) 第一階段。2004年1月至2006年8月，庫水位在135～139 m波動，此時間段水位升降具有規律性，監測點位移主要受降雨量影響，位移增長速率趨于平穩。

(2) 第二階段。2006年9月至2008年9月，此階段后水位上升到一個新的高度，水位的上升對坡體的滲流場和應力場以及巖土體的結構都產生較大的影響。這種影響在第一次庫水位從155 m下降到145 m時較為明顯。

(3) 第三階段。2008年10月至2012年9月，庫水位在145～175 m范圍內波動，滑體適應了降雨與庫水位的規律性變化，監測點最大位移增加速率出現在庫水位下降及夏季降雨集中時段，滑坡進行了長期的應力調整，位移增長逐漸變得規律。

圖5 地表裂縫Fig.5 Ground surface crack

4 位移預測

4.1 趨勢項位移的提取與預測

趨勢項位移反映了滑坡位移的長期變化規律，采用移動平均法分解趨勢項和周期項，設原始時間序列為Si={s1,s2,…,st}，趨勢項的計算方法為

(17)

式中：φ(i)為趨勢項位移提取值；n為周期值，鑒于三峽地區降雨量與庫水位隨季節呈周期性變化，這里取周期為12，提取的趨勢性位移和周期性位移如圖6所示。采用灰色Verhulst模型預測八字門滑坡趨勢項，模型選擇2009年1月至2012年1月數據作為模型訓練，預測2012年2月至2012年9月的趨勢項位移，每預測一月，將這組數據加入訓練組，用于預測下一月位移，以保證模型輸入數據的不斷更新。預測結果如圖7所示，監測點ZG111預測值平均相對誤差為0.44，可見灰色Verhulst模型預測位移趨勢項具有較好的效果。

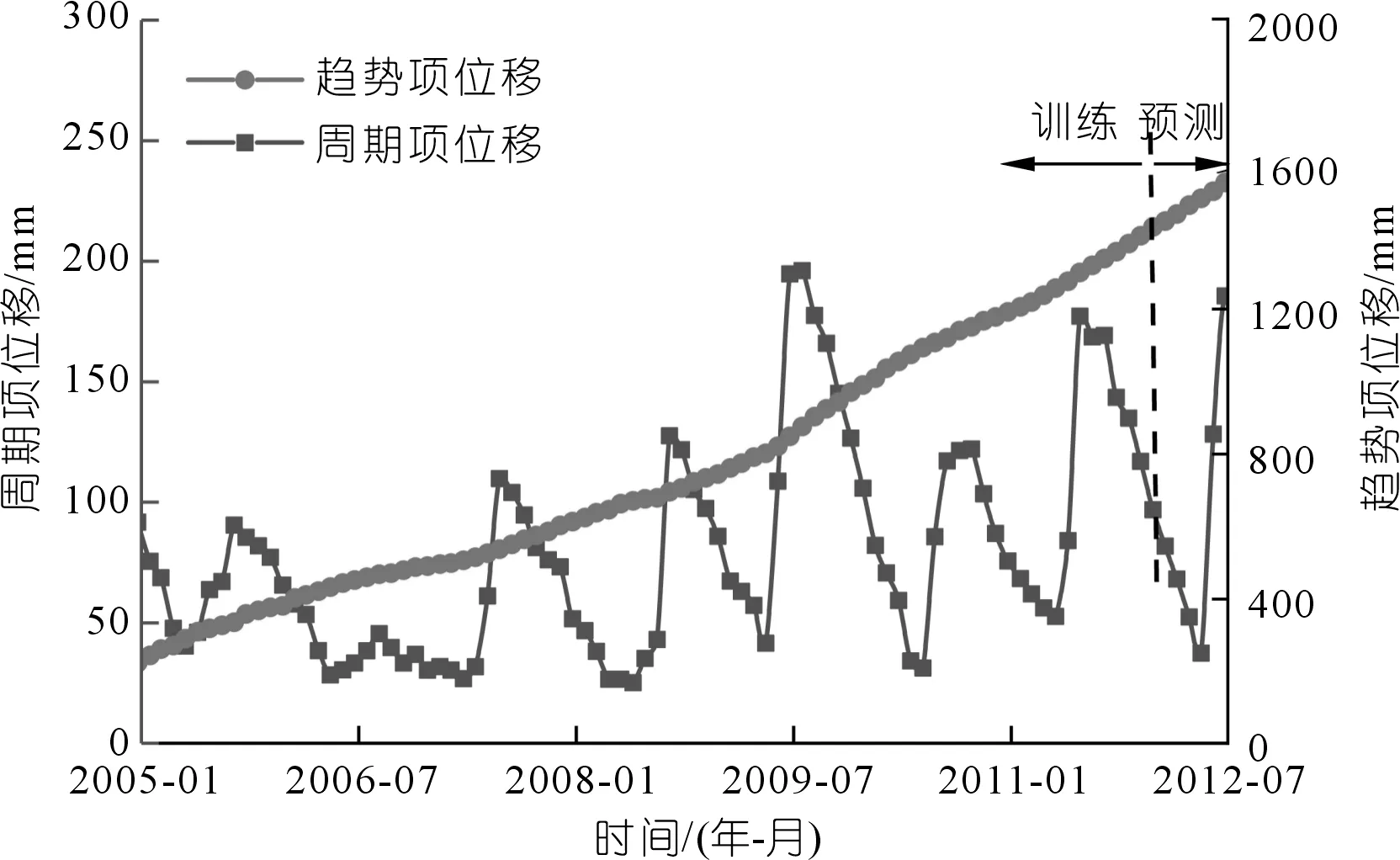
圖6 趨勢項位移和周期項位移提取值Fig.6 Extracted values of trend displacement and periodic displacement

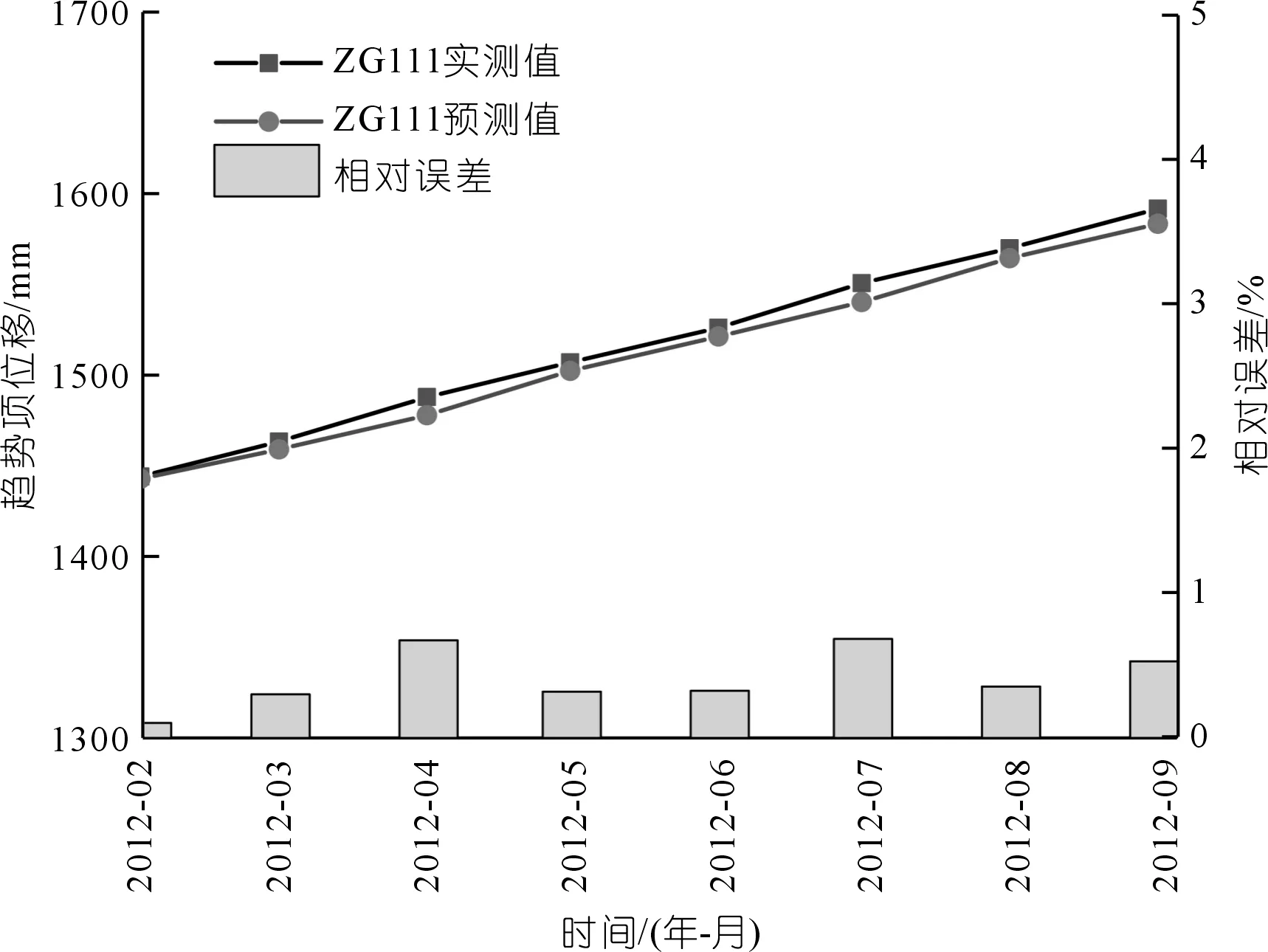
圖7 趨勢項位移預測結果Fig.7 Predicted values of trend displacement

4.2 周期項的預測

4.2.1影響因子的選取

影響因子的選取對滑坡位移預測的效果至關重要，八字門滑坡周期性位移的影響因素除了降雨量、庫水位外，坡體的狀態也會對環境變化有著不同的響應[10]。

(1) 降雨量。季節性降雨是誘導位移呈周期性變化的重要因素。一方面，降雨產生的地表水對坡面土壤有沖刷和搬運作用；另一方面，降雨入滲后改變了坡體的容重、動靜水壓力和巖土體強度。如圖8(a)所示，由于降雨入滲是一個緩慢的過程[10]，周期性位移與當月降雨量和兩月降雨量變化相關性都較大，故可以選取位移時間點當月和兩月的降雨量作為影響因子。

(2) 庫水位。八字門滑坡土質主要為含礫黏性土，滲透性能較差。當三峽水庫蓄水時，地下水向坡體內滲透，水位與滑坡體內地下水位形成負落差，對坡腳有著反壓作用，有利于邊坡穩定；在庫水位下降時，效果相反，使滑塊的變形速度加快[12]。如圖8(b)所示，庫水位對滑塊的變形影響還有一定的滯后性，因此選擇庫水位高程、當月庫水位變化和雙月庫水位變化作為影響因子。

(3) 邊坡狀態。坡體不同的狀態也會對外界變化響應不同。當邊坡處于穩定狀態時，強烈的外界變化對邊坡影響也較小；當滑坡處于臨界狀態時，輕微的外界變化也能產生巨大的影響，選取上月周期項位移量用于表征坡體狀態。

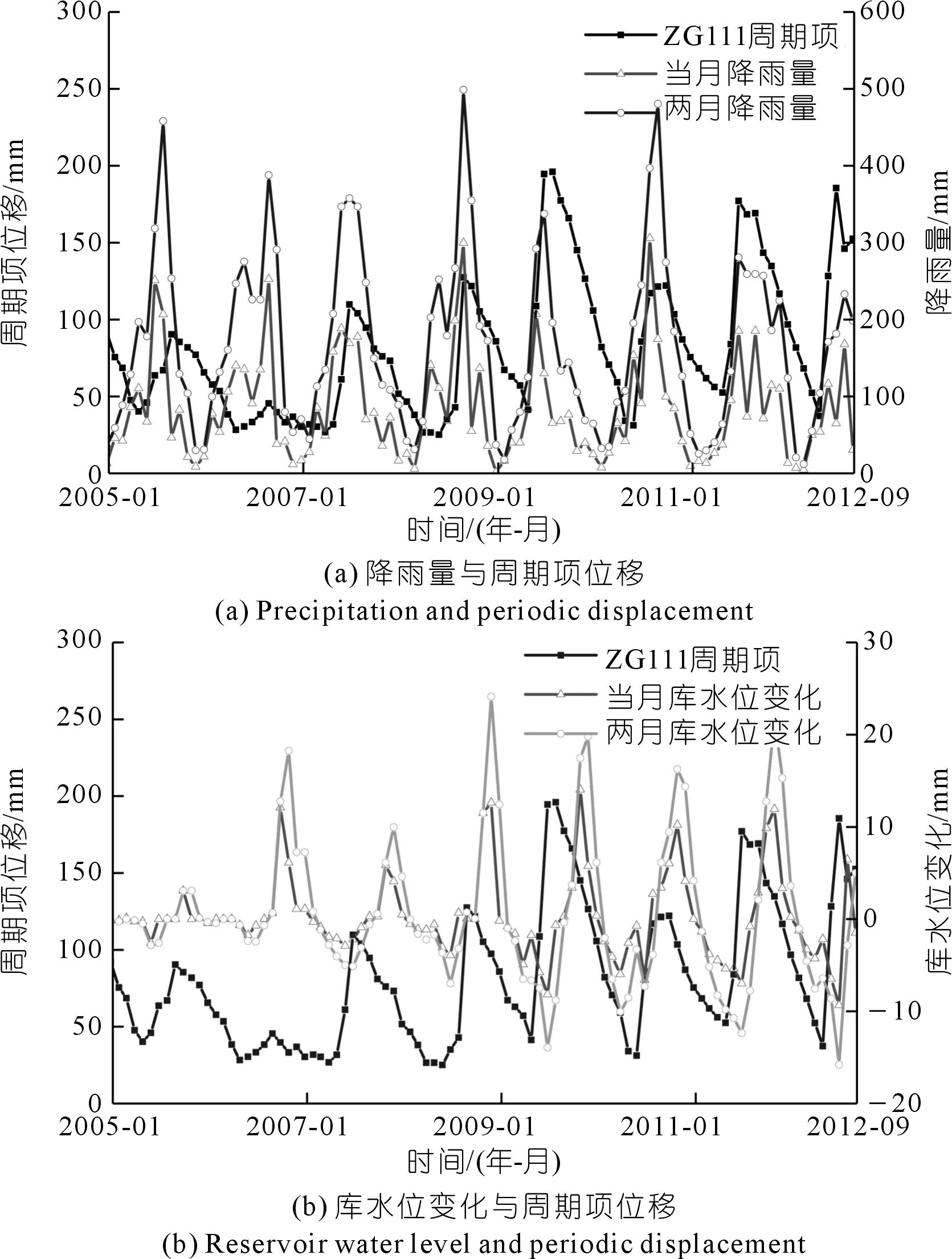
圖8 周期項位移與影響因子關系Fig.8 Relationships between periodic displacement and influence factors

為驗證影響因子的合理性，用灰色關聯度法分析各影響因子的關聯度，結果發現月降雨量、雙月降雨量，庫水位高程、月庫水位與周期項位移關聯度均超過0.6，表明所選影響因子與周期項是密切相關的。

4.2.2GRU模型的建立及參數的選取

將八字門滑坡位移數據樣本劃分為訓練集和預測集，數據從2005年1月至2012年9月，一共93組樣本數據，訓練集取前85組，后8組用于檢測模型的預測能力。

將選取影響因子作為輸入，周期性位移作為輸出。為消除量綱對預測性能的影響，將樣本數據歸一化到[0.1，0.9]。使用Keras框架搭建GRU模型，利用python進行程序編寫。該模型包含4層神經網絡，前3層為GRU層，第4層為Dense層。輸入序列長度對模型的精度有重要的影響[26]，控制著滑坡位移使用的歷史數據的個數，通過對不同輸入序列長度的試算，選擇輸入序列長度為3。

4.2.3周期性位移預測結果對比

為驗證新模型的預測效果，采用已在滑坡預測方面取得較好效果的GRNN模型進行對比預測分析[27]。數據處理方式與GRU模型相同，GRNN模型使用MATLAB2012a進行程序編寫。

周期項的位移預測結果如圖9所示，各模型的預測精度見圖10。

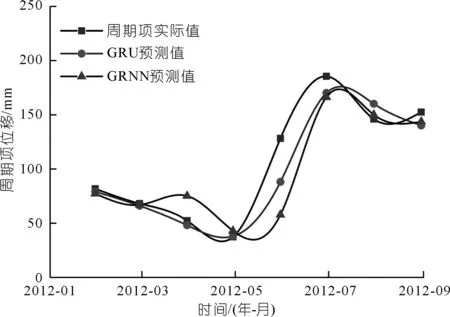
圖9 周期項位移預測結果Fig.9 Predicted values of periodic displacement

GRU模型預測結果的擬合優度和均方根誤差分別0.858和21.9 mm，最大誤差點出現在2012年6月，此時降雨量增多，庫水位下降，影響因素變化過大。盡管GRU模型仍有少數月份效果不佳，但對于三峽水庫滑坡“階躍性”特征的預測效果較好。而GRNN模型預測結果的擬合優度和均方根誤差分別為0.768和25.0 mm，精度均低于GRU模型的精度。具體原因分析如下：① 由于GRNN模型的本質為靜態回歸模型，而GRU模型獨特的門循環結構，使得當前預測值受當前輸入信息和歷史信息的影響，這是傳統神經網絡結構不具有的；② GRNN模型的訓練過程是根據輸入影響因素與位移的對應關系訓練調整，當影響因子有較大變化時，模型的預測效果難以保證，如圖10所示，在位移“階躍”階段，GRU模型的效果較GRNN更好。

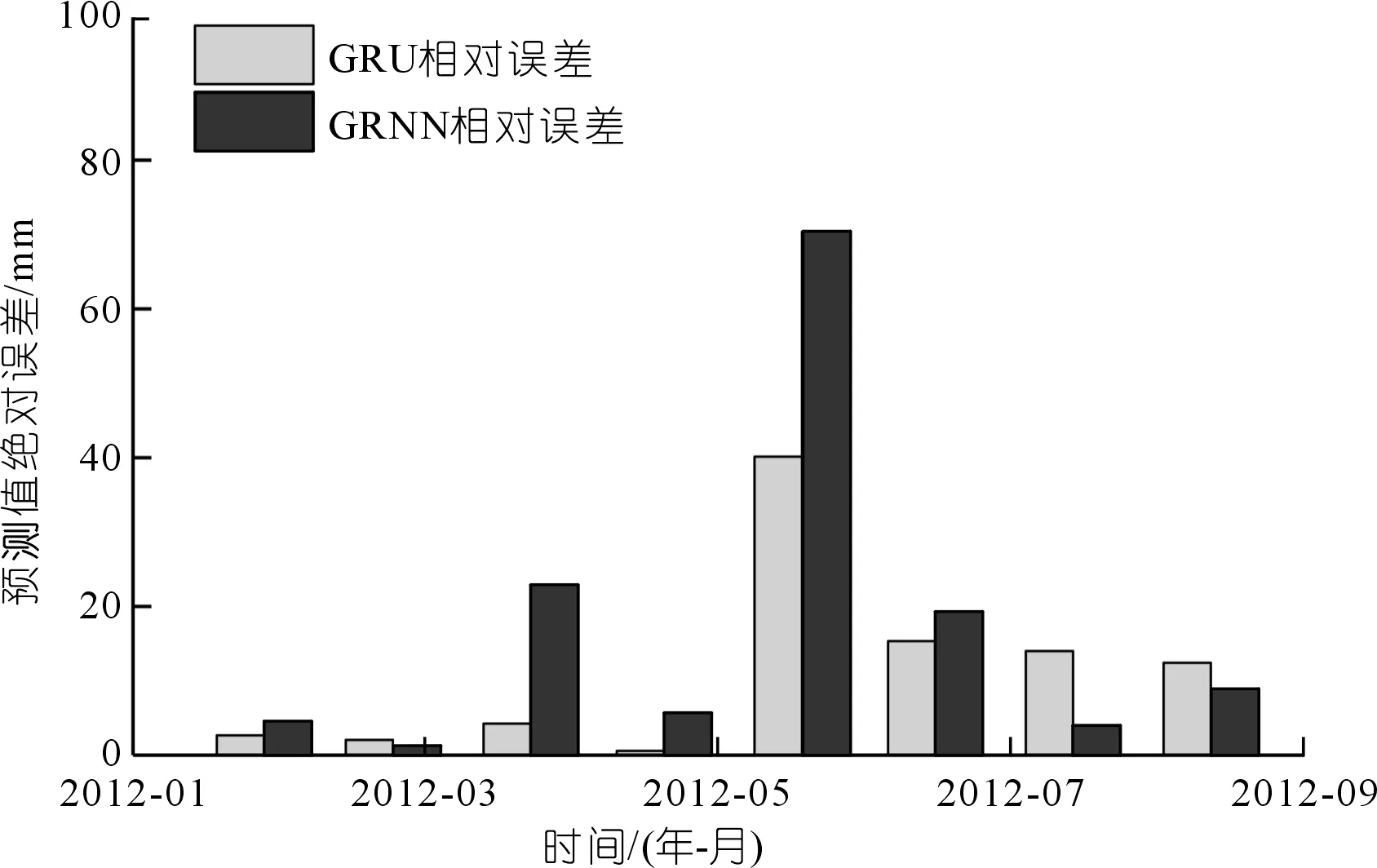
圖10 兩種模型的相對誤差Fig.10 Absolute error of the two models

4.3 滑坡累計位移的預測

根據時間序列的分解原理，位移趨勢項與周期項之和是滑坡位移值。如圖11所示，預測位移與實際位移變化接近一致，ZG111監測點預測位移的擬合優度為0.987。從預測效果來看，累計位移預測值誤差最大的點與周期項誤差最大的點均出現在6～7月，表明周期項的預測精度對累計位移的預測效果至關重要。

滑坡位移值由趨勢項和周期項疊加得到的，趨勢項變化是邊坡自身發展的外在表現，灰色Verhulst屬生物演化模型[3-5]，對于趨勢項變化過程具有較好的擬合效果。周期性位移反映了外界因素變化，而GRU模型獨特的門循環結構對處理時序問題具有獨特的優勢。2003三峽水庫首次蓄水后，位移小幅增長；2008年蓄水水位升高后，位移開始快速增長，在多年規律性的庫水位調度下，逐漸形成新的平衡，位移再一次進入規律性增長[25]。由圖11可知，目前累計位移的變化仍受周期項變化主導，而庫水位高程為人為控制因素，故降雨量為現階段需要密切關注的影響因子。

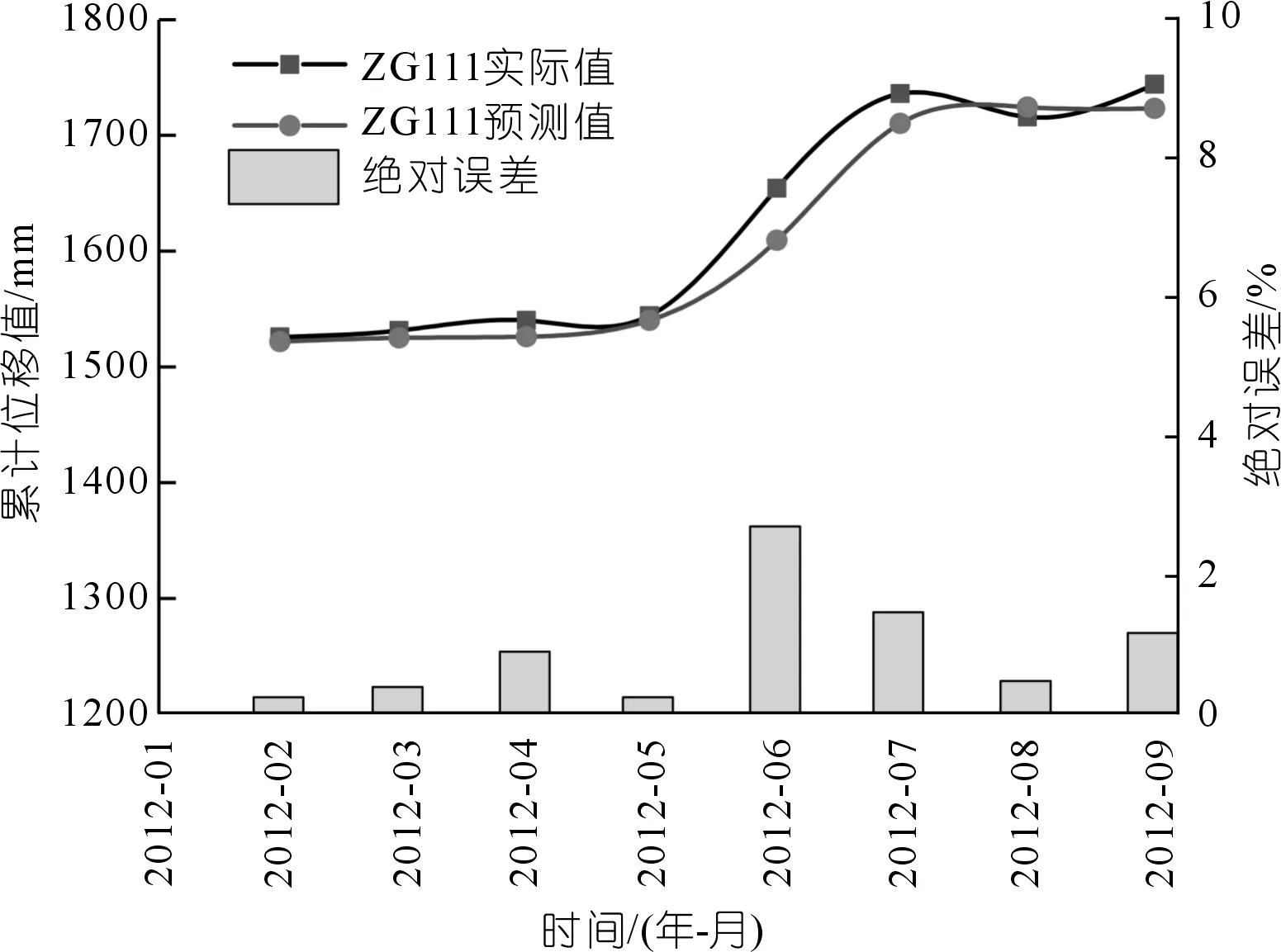
圖11 滑坡累計位移實際值與預測值Fig.11 Measured values and predicted values of accumulative displacement of landslide

5 結 論

針對滑坡位移這一非線性變化時間序列，提出了一種基于時間序列和GRU網絡的滑坡位移預測模型，將模型用于預測三峽庫區八字門滑坡，獲得以下結論。

(1) 基于時間序列分離了滑坡位移中的趨勢項和周期項，灰色Verhulst模型能夠較好地描述趨勢項演化特征，而GRU模型能夠儲存和利用歷史信息，在考慮影響因子的滯后性方面，不僅充分考慮了前兩月的輸入數據，還可以利用之前月份的輸入信息，相較于傳統的ANN網絡，從理論上提高了有限數據的利用率。

(2) GRU模型與靜態的GRNN模型相比，GRNN模型僅能考慮當前輸入信息，所以在影響因子變化劇烈時，對于突變點的預測效果不佳，處理時間序列問題的能力弱于GRU模型。

(3) 三峽庫區八字門滑坡位移預測工程實例表明，獨特的記憶結構能夠在訓練過程中自動適應監測點的歷史信息，實現了模型的狀態反饋，適用于三峽庫區“階躍性”滑坡，可為此類滑坡位移預測提供重要的參考。