堆石料縮尺效應試驗研究

劉 賽 朝，吳 鑫 磊，徐 衛 衛，石 北 嘯

(1.河北工程大學 水利水電學院，河北 邯鄲 056021； 2.南京水利科學研究院 巖土工程研究所，江蘇 南京 210029)

隨著高土石壩建設高度的不斷增加，其施工技術和建設要求不斷提高，這就對堆石料的強度和變形等關鍵性指標提出了更高的要求。土石壩施工現場所用的堆石料最大粒徑已經超過1 000 mm，而目前國內三軸儀的最大直徑為1 000 mm，堆石料的試驗最大粒徑為200 mm，這就必須考慮對超出粒徑范圍的顆粒進行縮尺，以滿足室內試驗的要求。國內外已有的針對堆石料縮尺效應研究成果普遍認為，縮尺會高估原型建筑的強度[1-3]，也有學者的研究成果得出相反的結論[4-5]，這可能與各研究者所采用的原始級配、母巖性質密實度控制標準、縮尺方法和試樣飽和程度各不相同有關[6]。目前，國內大多研究都是針對最大粒徑為60 mm、試樣直徑為300 mm的常規三軸試驗，在進行大比例縮尺后，最大粒徑減小、顆粒數目增多，這就不可避免和實際工程產生較大的誤差。孔憲京等[7]對比了超大型三軸和大型三軸剪切試驗，認為縮尺會放大原型的強度且縮小應變。袁鐵柱等[8]對粗粒料的抗剪強度進行了研究，認為抗剪強度與試樣飽和程度有關。姜景山等[9]認為粗粒料濕化會增大變形。胡哲等[10]認為最大粒徑越大峰值偏應力和初始彈性模量越大，內摩擦角隨著粒徑的增大表現出先增加后減小的變化規律。Xiao等[11]認為，對原級配堆石料進行縮尺后，會低估原級配的變形程度，從而高估了大壩的安全性。20世紀60年代以來[12-13]，美國和日本等國都研制出可進行最大粒徑為250 mm的超大型三軸儀，從原理來講，其試件最大顆粒尺寸越大就越接近現場情況，誤差也就會越小，但因超大型三軸儀的制樣方法尚未統一，試驗設備也非通用，試驗成果的代表性有待商榷。

本文采用超大型三軸和常規大型三軸開展堆石料三軸剪切試驗，試樣尺寸分別為Φ500×1 000 mm(最大粒徑為100 mm)和Φ300×700 mm(最大粒徑為60 mm)。對某堆石壩主堆石區堆石料進行不同最大粒徑尺寸的三軸剪切試驗，主要研究在采用等量替代法進行縮尺后，兩組試驗在凝聚力、內摩擦角、變形等方面的差異。

1 試驗方法

1.1 縮尺方法

目前常用的縮尺方法有4種，分別為剔除法、等量替代法、相似級配法和混合法。4種縮尺方法各有優缺點：剔除法使用簡單方便，但在超粒徑顆粒含量較多時，會很大程度改變原級配堆石料的工程特性，只宜在超粒徑料含量不大于 10%的范圍內使用；等量替代法具有保持粗顆粒的骨架作用及粗料的級配的連續性和近似性等特點，適用超粒徑含量小于40%的堆石料；相似級配法保持了級配關系(不均勻系數不變)，細顆粒含量變大，但不應影響原級配的力學性質的程度，一般來講，小于5 mm顆粒含量不大于15%～30%；至于采用何種縮尺方法，SL237-1999《土木試驗規程》中尚未明確規定。

等量替代法計算公式為

(1)

式中：Pi為等量替代后某粒組的含量；Poi為原級配某粒組的含量；P5為大于5 mm的粒徑含量；Pdmax為超粒徑的含量。

本文采用等量替代法進行縮尺，符合SL237-1999《土木試驗規程》中相關要求，主堆石區設計平均級配曲線如圖1所示。

圖1 設計級配及試驗級配Fig.1 Designed grading and test grading

1.2 試驗介紹

試驗儀器采用南京水利科學研究院的超大型三軸儀和大型三軸儀。允許試樣尺寸分別為Φ500×1 000 mm(最大粒徑100 mm)和Φ300×700 mm(最大粒徑60 mm)。試驗試樣采用某堆石壩主堆石區料場料，巖性為堆石料。

制樣采用分層法，共分10層進行裝填，使試樣保持排水條件，進行固結排水剪切試驗。剪切速率控制為2.0 mm/min。剪切過程中由計算機采集試樣的軸向荷載、軸向變形，并同步繪制應力-應變曲線，直至試樣破壞或至試樣軸向應變的15%。當應力-應變曲線有峰值時，以峰值點為破壞點，峰值點所對應的主應力差(σ1-σ3)f為該堆石料的破壞強度，反之則取軸向應變的15%所對應的點為破壞點，對應的主應力差(σ1-σ3)f為該堆石料的破壞強度，共進行5組不同圍壓的試驗，具體試驗制樣密度及試驗圍壓見表1。

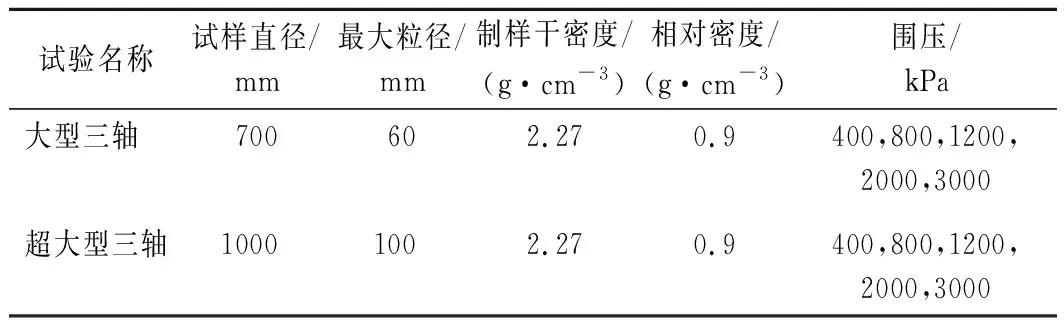
表1 試驗制樣密度及試驗圍壓Tab.1 Test sample density and test confining pressure

2 試驗成果及分析

2.1 應力-應變關系

圖2分別給出了超大型三軸和大型三軸剪切試驗在不同圍壓下應力比λ(λ=q/p，其中q為廣義剪應力，p為平均主應力)-軸向應變ε1曲線和體變εv-軸向應變ε1曲線。由圖2和圖3可知，隨著圍壓的增大，λ-ε1曲線向下移動，εv-ε1曲線向上移動，兩組試驗均表現出低圍壓剪脹、高圍壓剪縮，隨圍壓增大應力軟化逐漸減弱的特性。相同圍壓下，超大型三軸試驗后的λ-ε1曲線位于大型三軸試驗下方，說明大型三軸軟化強于超大型三軸，值得注意的是，隨著圍壓的增加，兩曲線趨于重合，故高圍壓下超大型三軸軟化增強速度大于大型三軸。相同圍壓下，超大型三軸的εv-ε1曲線位于大型三軸上方，說明大型三軸剪脹強于超大型三軸。

在相同圍壓下大型三軸軟化和剪脹均大于超大型三軸，這是因為粗粒土的剪脹和軟化與密度有關，兩組試驗的初始密度相同，由于超大型三軸顆粒較大，隨著加載的進行，超大型三軸的密度逐漸小于大型三軸，所以大型三軸剪脹和軟化均強于超大型三軸。

2.2 兩組試驗結果的強度差異特性

然后研究超大型三軸和大型三軸試驗條件下試樣的強度特性，圖3給出了兩組試驗破壞時的摩爾圓和強度包線圖。由圖3可知，超大型三軸和大型三軸試驗后試樣的凝聚力C分別為201.1，199.5 kPa，內摩擦角φ分別為39.7°和40.4°，超大型三軸試樣的凝聚力C比大型三軸大1.6 kPa，內摩擦角φ比大型三軸小0.7°，原因可能是超大型三軸顆粒大且棱角分明，顆粒之間咬合力大，而大型三軸顆粒小，顆粒數目多，接觸面積大，內摩擦大。

在堆石料中，凝聚力C表征顆粒間咬合力，顆粒越大凝聚力C越大。但顆粒越大，其棱角往往越分明，當試樣由大顆粒組成時，棱角處產生應力集中，越容易產生顆粒破碎，進而影響材料強度。

圖2 應力比λ與軸向應變ε1及體變 εv與軸向應變ε1關系Fig.2 εv-ε1 and λ-ε1 relations of test rockfills

圖4給出了峰值應力(σ1-σ3)f隨圍壓σ3變化的關系。由圖4可知，兩組試驗的破壞應力均隨圍壓的增高而增高，且兩組曲線大致呈線性關系，當圍壓相同時大型三軸峰值應力大于超大型三軸，且隨著圍壓的增加，峰值應力相差越來越大。

2.3 兩組試驗結果的變形差異

堆石料變形力學性質的研究對工程具有重大意義。為研究堆石料的變形特性，圖5給出了初始變形模量Ei與圍壓σ3的關系，圖6給出了初始泊松比Vi與σ3/Pa關系(Pa為標準大氣壓強，本文取101.325 kPa)。其中Ei定義為ε1=0時(σ1-σ3)與ε1關系曲線切線的斜率，Vi定義為ε1=0時徑向應變與軸向應變切線的斜率。

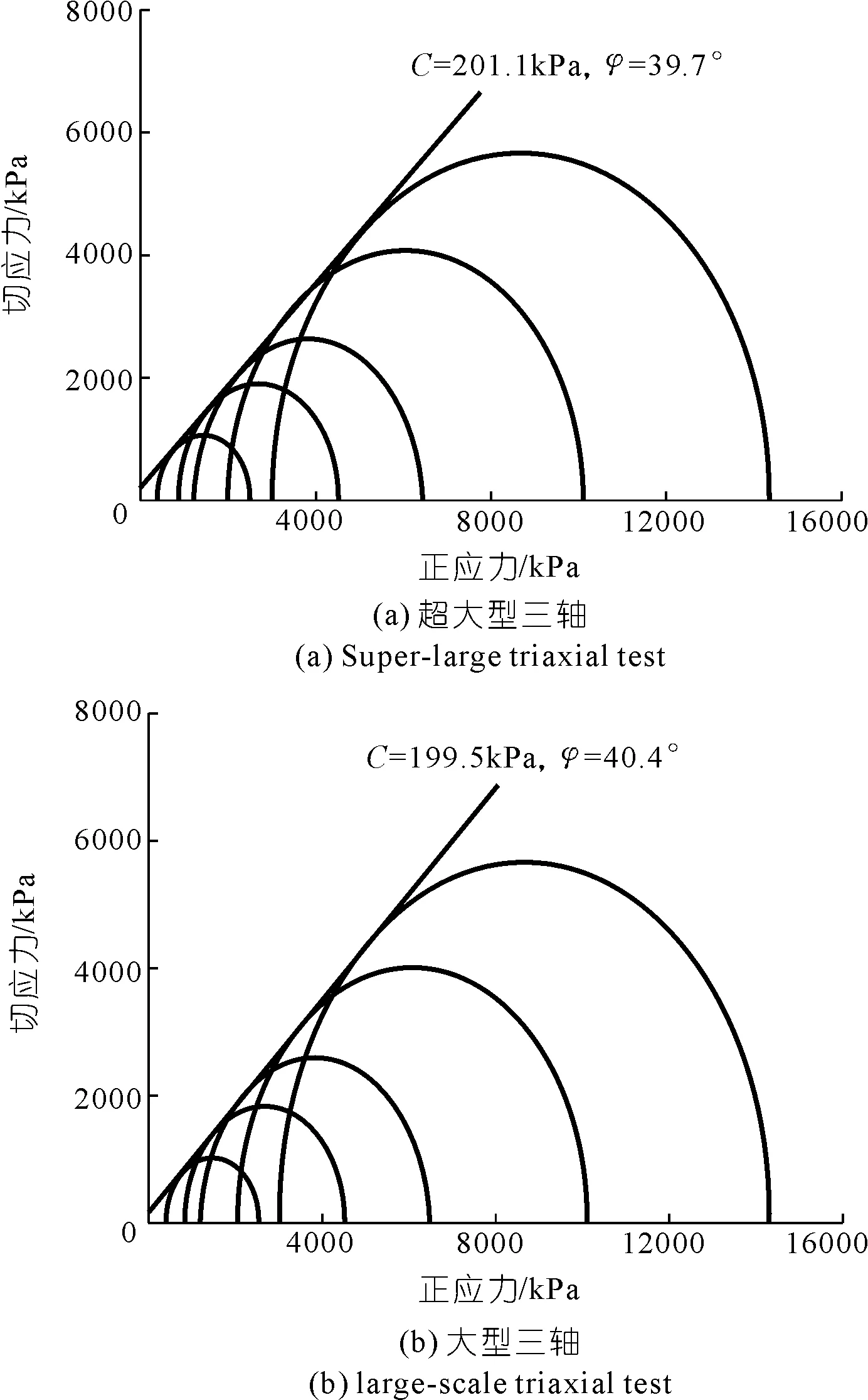
圖3 超大型三軸和大型三軸試驗摩爾圓及強度包線Fig.3 Mohr circle and strength envelope

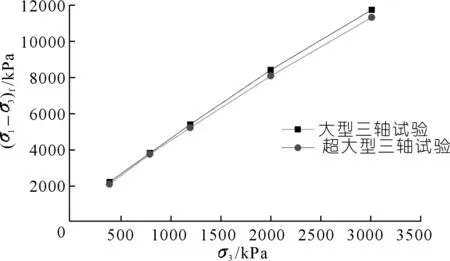
圖4 (σ1-σ3)f與σ3關系Fig.4 Relationship between peak strength and confining pressure

由圖5可知，兩組試驗的初始變形模量Ei均隨圍壓σ3的增加而呈現出非線性增加的趨勢，Ei與σ3之間具有良好的冪函數關系；在低圍壓時(σ3<1 200 kPa)，大型三軸的Ei大于超大型三軸，高圍壓時(σ3≥1 200 kPa)，大型三軸的Ei小于超大型三軸。其原因可能是低圍壓時超大型三軸顆粒較大，顆粒更易產生顆粒破碎，顆粒間位置錯動大，抵抗變形能力弱一些，表現出較小的變形模量；高圍壓時超大型三軸中較大顆粒已經破碎，顆粒排列更加緊密，顆粒間嵌入和咬合力大，在外力作用下不易發生位置調整，土體吸收大部分能量用于克服顆粒間的摩擦和咬合作用，土體抵抗變形的能力要強一些，表現出較大的變形模量。

由圖6可知，兩組試驗的初始泊松比Vi均隨圍壓σ3的增加非線性減小，且呈現出良好的二次多項式關系。相同圍壓下，超大型三軸的泊松比Vi大于大型三軸，隨著圍壓的增加，兩曲線距離越來越近，超大型三軸初始泊松比Vi下降速度大于大型三軸。分析原因，可能是因為超大型三軸顆粒較大，顆粒更易產生破碎，產生較大的變形。故在實際工程中，應該考慮室內試驗計算所得變形可能較實際工程較小。

圖5 初始變形模量Ei與圍壓σ3關系Fig.5 Relationship of Ei and σ3

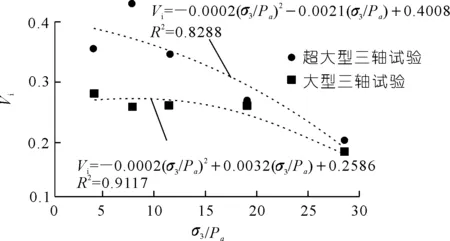
圖6 初始泊松比Vi與σ3/Pa關系Fig.6 Relationship of Vi and σ3/Pa

2.4 鄧肯張E-B模型參數

對兩組試驗成果進行整理，并將整理的鄧肯張E-B模型參數結果列于表2。從表2中可以看出，超大型三軸φ0高于大型三軸0.4°，大型三軸Δφ高于超大型三軸0.2°，超大型三軸與大型三軸強度指標相差不大。

表2 鄧肯模型參數Tab.2 Duncan model parameters

大型三軸的彈性模量參數k以及體積模量參數Kb分別比超大型三軸的高出16.92%和9.44%。大型三軸試驗的變形模量n小于超大型三軸試驗說明前者初始模量隨圍壓增幅小于后者；二者體積模量指數m分別為0.26和0.27，說明兩者體積模量相差不大。由兩組試驗鄧肯張參數對比可知，采用超大型三軸計算會得到更大的變形。

3 結 論

采用超大型三軸(最大粒徑100 mm)和大型三軸(最大粒徑60 mm)試樣分別開展室內三軸剪切試驗，系統研究了堆石料的縮尺效應，得到的主要結論如下：

(1) 超大型三軸試驗中試樣的內摩擦角比大型三軸的低0.7°，強度指標相差不大。超大型三軸中試樣的峰值應力比大型三軸低，且隨著圍壓的增高，峰值應力相差越來越大。

(2) 鄧肯張E-B模型參數中，大型三軸中試樣的彈性模量參數k和體積模量參數Kb較超大型三軸的分別提高16.92%和9.44%。由此可見，采用大型三軸試驗結果計算會高估壩體的實際變形，且高估了堆石料的實際強度，在土石壩強度分析中會得到偏于危險的結論。

(3) 分析發現，無論是超大型三軸還是大型三軸試驗結果，鄧肯張E-B模型參數中的初始彈性模量Ei與圍壓σ3之間均呈良好的冪函數關系。但兩者圍壓不同時的表現不同，低圍壓時(σ3<1 200 kPa)，大型三軸試樣的Ei大于超大型三軸，高圍壓時(σ3≥1 200 kPa)，大型三軸試樣的Ei小于超大型三軸。

本文僅對一種堆石料進行研究，且未系統、定量地研究顆粒破碎對縮尺效應的影響。對于不同巖性的堆石料縮尺效應及顆粒破碎對縮尺的影響，還有待進一步研究。