磁控二氧化鈦憶阻混沌系統及其電路設計

許向亮,李國東,2,戴婉瑩

(1.新疆財經大學 統計與數據科學學院,新疆 烏魯木齊 830012;2.桂林電子科技大學 數學與計算科學學院,廣西 桂林 541004)

1971年,Chua首次提出憶阻器是一種磁通與電荷相關的元件[1]。2008年,惠普公司的研究人員首次在實驗室做出憶阻器實物[2],并在后續實驗得出了憶阻器的記憶原理[3],憶阻器的阻值是流經它的電荷所確定的。納米憶阻器的出現,有望實現非易失性隨機儲存器。由于納米憶阻器的隨機儲存器的集成度、讀寫速度、功耗較傳統隨機儲存器更為優越,得到了研究人員的廣泛關注,目前已有大量的文獻對荷控型和磁控型憶阻器的數學模型[4-8]以及憶阻混沌系統的SPICE模型[9]進行了報道,但是這些模型并不能較好地應用于實際電路,因此建立了各類相關憶阻器的替代模型和等效電路,分別采用離子遷移、壓控憶阻器等方法實現混沌電路的雙穩性[10]和語音信號的保密通信[11]。在以上所述的研究成果中,基于磁控制構建的仿真器并不常見,基于磁控模型的憶阻電路是未來構建復雜混沌系統的趨勢,因此,研究磁控憶阻器模型具有重要意義。依據憶阻器原理,構建二次、三次、分段非線性模型憶阻器引入傳統混沌系統,如Lorenz系統[12]、蔡氏混沌電路[13]、多渦卷Jerk系統[14]、文氏電路[15],豐富了構建憶阻混沌系統的方法。近年來,在傳統混沌的基礎上提出了許多基于磁控二氧化鈦憶阻器的混沌系統[16-18],當系統出現多穩態[19]現象時,其具有復雜的拓撲結構和動力學行為,可用于圖像加密[20]。且隨著憶阻混沌系統在通信保密領域的廣泛應用,系統參數的選擇顯得尤為重要,系統參數的選擇會影響混沌信號的偽隨機性。本文嘗試采用混沌圖和復雜度分析結合的方法得到了系統的最優參數,該方案具有普適性,便于廣泛推廣。

本文提出了一種結構簡單的憶阻混沌系統,采用磁控二氧化鈦憶阻器來構建混沌系統的非線性項,詳細地分析了該系統的動力學行為。系統存在特殊的分叉結構,雙層分叉或者類周期性窗口可以保證系統的混沌特性,在分叉斷層區間,系統的Lyapunov指數較小,采用混沌圖、復雜度分析等方法能夠得到該區間混沌系統的最優參數取值范圍,且在最優參數范圍控制下的憶阻混沌系統,其多穩態共存現象更加顯著,從而驗證了該系統可以產生豐富的動力學行為,并用Multisim實現了該系統的混沌電路仿真,其實驗結果驗證了數值仿真的正確性。

1 磁控二氧化鈦憶阻器混沌系統及其動力學分析

1.1 基于磁控二氧化鈦憶阻器的混沌系統模型

本文提出的一種帶有磁控二氧化鈦憶阻器的混沌系統,其狀態方程描述如下:

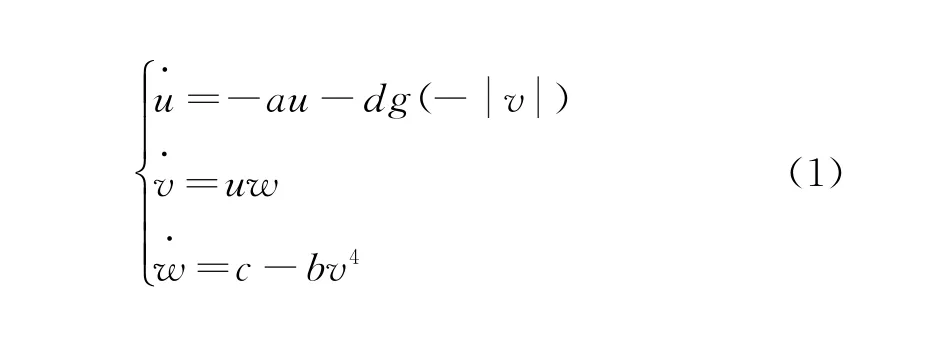
式中:u,v,w∈R為該憶阻混沌系統的狀態變量;a,b,c,d為系統參數;g(·)為系統的非線性項。磁控二氧化鈦憶阻器的電荷編碼[9]如下:

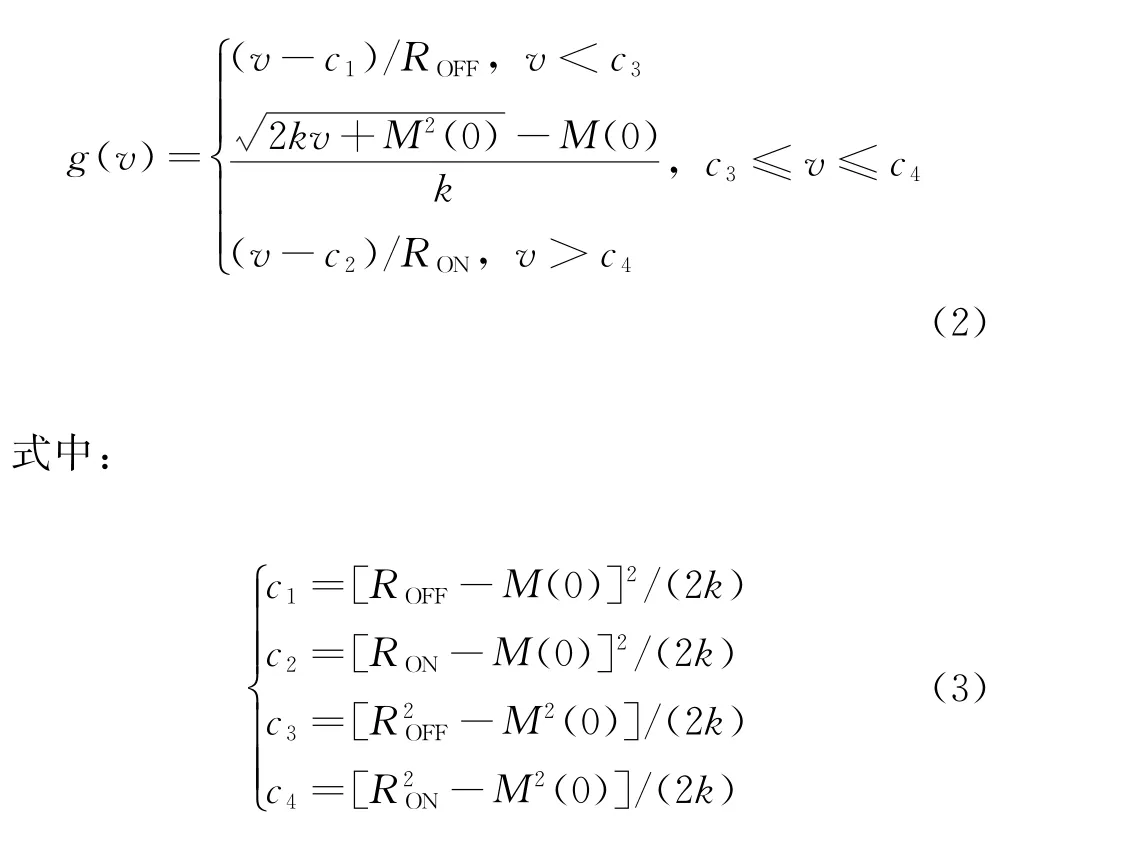
式中:v表示輸入憶阻器的磁通;RON和ROFF分別代表憶阻器的兩個極限值;M(0)為憶阻器的初始值;k=[(RON-ROFF)×μvRON]/D2,其中D是薄膜厚度;μv是所用憶阻器模型中氧空位的平均遷移率。設置憶阻器的參數如下:RON=100Ω,ROFF=20 kΩ,M(0)=15 kΩ,μv=10-14m2·s-1·V-1,D=10 nm,當系統的初始狀態(u,v,w)=(0.6,0.2,0.3)時,參數a=6,b=8,c=50,d=105,該系統處于混沌狀態。設置時間為10 s,采用龍哥庫塔法利用Python3.7對系統(1)進行仿真,得到管狀3D圖。系統在保留初始狀態的基礎上添加微小改動,呈彩色狀分布,分別得到u-v平面、u-w平面、v-w平面的相圖,如圖1所示。

1.2 憶阻混沌系統的動力學分析

1.2.1 對稱性分析與耗散度分析

由系統(1)的相圖可知,系統存在對稱性,即(u,v,w)→(-u,-v,w),系統保持不變,關于w軸對稱,它滿足f(PT)=Pf(T),其中R表示三個維度,T表示系統(1)的狀態方程,P為變換矩陣,其變化可表示為:

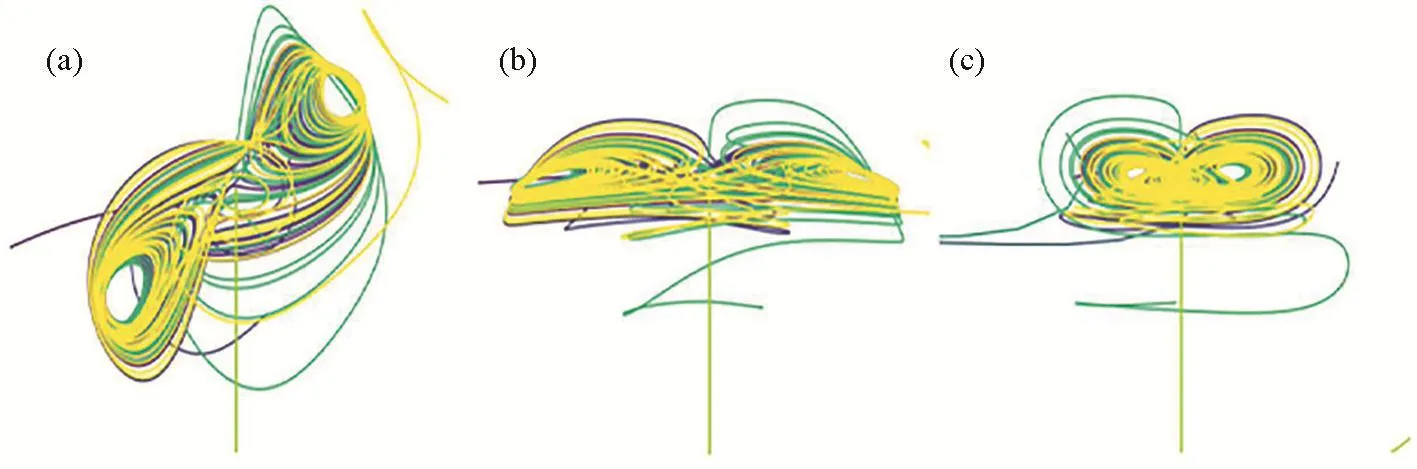
圖1 系統(1)的混沌吸引子。(a)u-v平面;(b)u-w平面;(c)v-w平面Fig.1 Chaotic attractor of system(1).(a)u-v plane;(b)u-w plane;(c)v-w plane

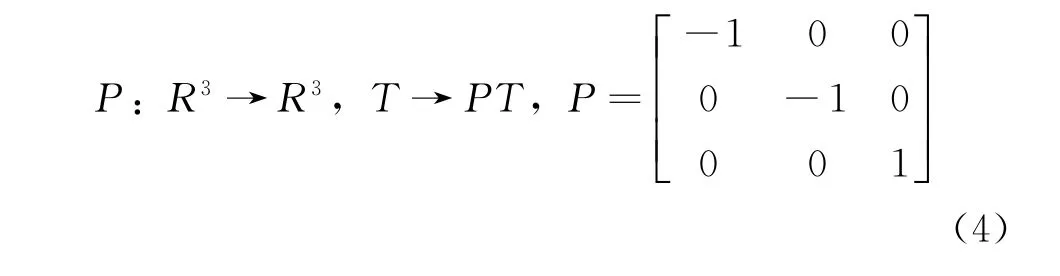
系統(1)的耗散度計算如下:

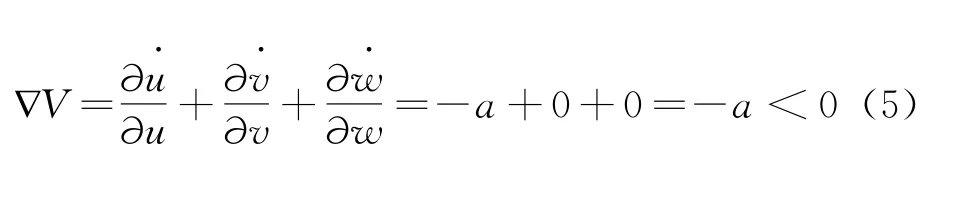
當系統(1)的參數a＞0,此時系統是耗散的,系統(1)是有界的,其軌道變化收縮率為:

也就是說一個初始值狀態下為V(0)的體積元在t時刻收斂速度為e-a,當t→∞時,系統運動軌跡上的每一個微小體積元都將以e-a指數倍速率快速收斂到零,本文選取系統的參數為:a=6,符合上述形式,該系統運動的軌跡線,最終會被控制在一個體積為零的極限集合,漸進運動吸引到固定的值上,說明該系統存在吸引子。

1.2.2 平衡點的穩定性

為了求解系統(1)的平衡點,令系統(1)變為齊次狀態方程。即:

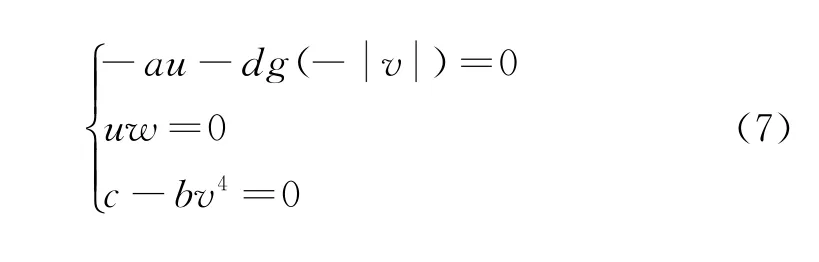
令a=6,b=2,c=50,d=105,此時系統有三個平衡點:S1(0,0,0),S2(2.2361,2.2361,0),S3(-2.2361,-2.2361,0)。

系統(1)的線性化Jacobian矩陣為:

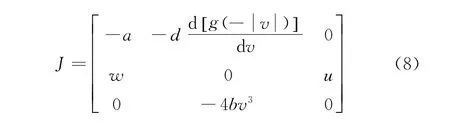
令系統(1)特征方程det(J-λI)=0,系統在平衡點S1(0,0,0)處的特征根λ1=1.4536,λ2=-1.2145,λ3=-7.2254。其中因為λ2,λ3為負實數根,λ1為正實數根,所以系統平衡點S1(0,0,0)是一個不穩定的鞍焦點。

在平衡點S2(2.2361,2.2361,0)處的特征根λ1=1.5811,λ2=1.4571+0.9823i,λ3=1.4571-0.9823i;λ2,λ3為一對共軛負數根,λ1為正實數根,所以系統平衡點S2(2.2361,2.2361,0)是一個不穩定的鞍焦點。

在平衡點S3(-2.2361,-2.2361,0)處的特征根λ1=1.5811,λ2=1.4571+0.9823i,λ3=1.4571-0.9823i;λ2,λ3為一對共軛負數根,λ1為正實數根,所以系統平衡點S3(-2.2361,-2.2361,0)也是一個不穩定的鞍焦點。

1.2.3 Lyapunov指數譜和維數

Lyapunov指數是衡量非線性動力學系統特性的一個重要的定量指標,它計算了相空間中相鄰運動軌道間收斂或發散的平均指數率,且一個正的Lyapunov指數意味著在系統的相空間中相鄰兩條軌道之間的差別隨時間的演化而呈現指數級分離且無法預測。設置系統(1)的初值狀態為(u,v,w)=(0.6,0.2,0.3),且設置系統參數為a=6,b=8,c=50,d=105,選取時間t=300 s,采用雅可比矩陣的方法得到如圖2的Lyapunov指數譜,該系統具有一個正的λ1=1.133,一個趨近于0的λ2=-0.0099968,一個負的λ3=-7.1222,且滿足λ1+λ2+λ3＜0,此時該系統處于混沌狀態。

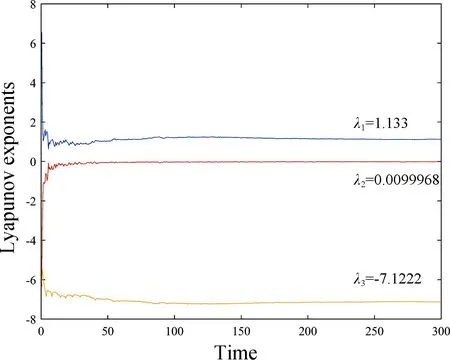
圖2 系統(1)的Lyapunov指數譜Fig.2 Lyapunov exponential spectrum of system(1)

依據Yorke公式計算Lyapunov維數:

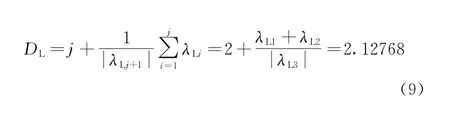
系統(1)出現分數維,此時系統處于混沌狀態。

1.2.4 功率譜和龐加萊截面

當系統(1)參數a=6,b=8,c=50,d=105時,取(u,v,w)初值狀態為(0.6,0.2,0),t=2000 s時,圖3的(a)、(b)分別為該系統的功率譜和龐加萊截面。其功率譜圖具有連續尖峰和噪聲背景的特征,從而驗證此系統為混沌系統,此外,Poincare截面映射保持了原系統的周期和準周期軌道的許多特性,且具有低維狀態空間。從系統(1)的Poincare截面映射呈現出成片的具有分形結構的密集型連續點,與其他系統不同的是,該系統的吸引域呈現旋轉形狀,且在最外層出現分段現象,因此該系統可能存在多穩態共存的現象。

1.3 分叉圖

1.3.1 雙分叉區域分析

設置系統參數a=6,c=50,d=105,令b為控制變量,控制區間為 [0,50],步長為0.05,初始狀態(u,v,w)=(0.6,0.2,0.3),其分叉圖如圖4所示。

圖3 系統(1)的功率譜和龐加萊截面。(a)功率譜;(b)龐加萊截面Fig.3 Power spectrum of system(1).(a)The power spectrum;(b)The Poincare map

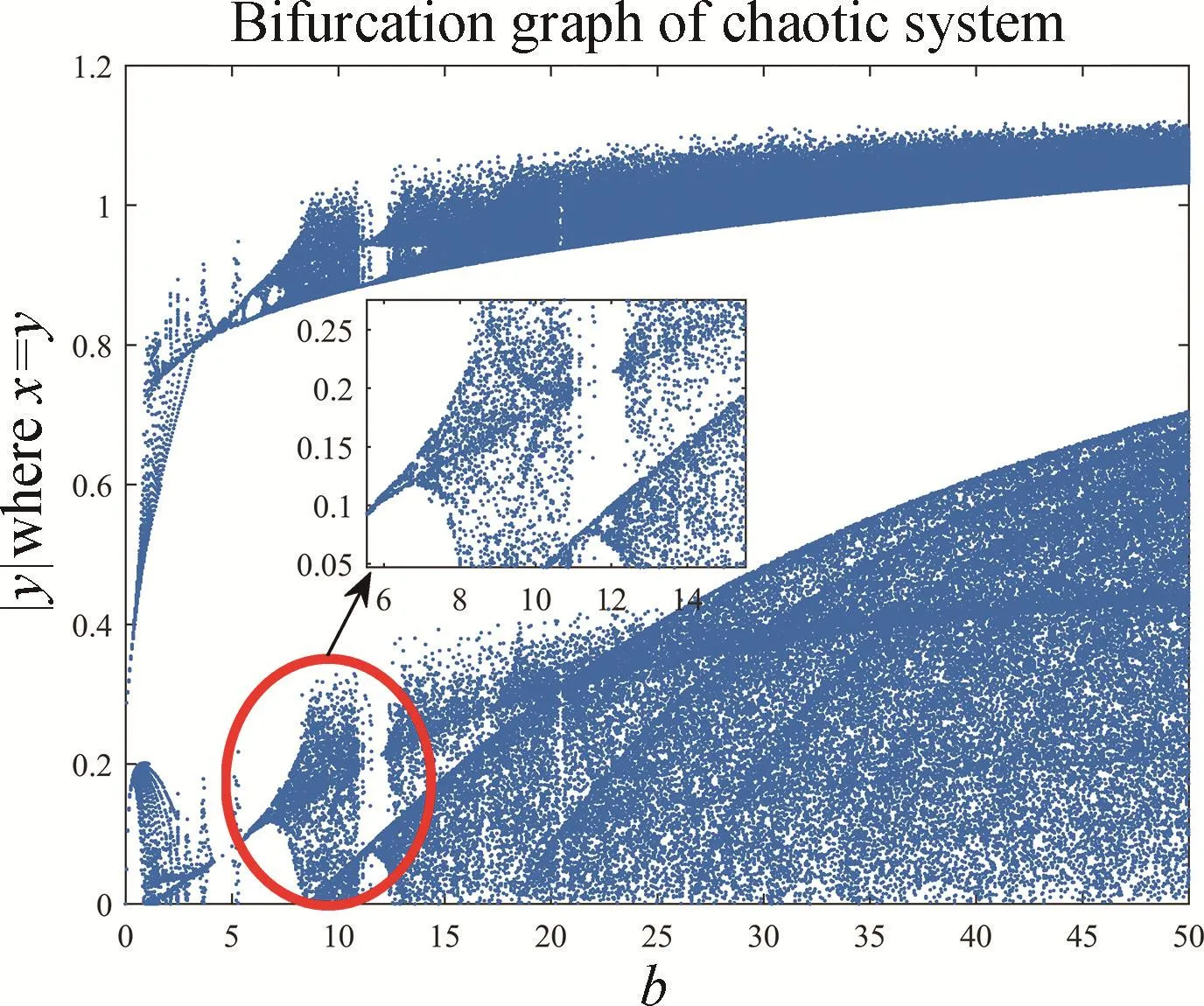
圖4 系統(1)的分叉圖Fig.4 Bifurcation diagram of system(1)

其分叉圖呈現分區域狀態,出現雙分叉現象,其中上層比下層的點數密集,因此參數在該區域的取值不會影響混沌的狀態,此時混沌的軌道仍會呈指數級分離,不會向單軌道遷移。在區間 [6,15],對分叉圖進行放大處理,混沌分叉出現自相似性,仍舊出現分叉斷層現象。

1.3.2 分叉斷層區域分析

為了進一步探究混沌軌道是否會在此區域出現單軌道遷移,采用1.3.1中設定的系統參數,在分叉圖的放大區間保留兩種初始值狀態(參考表1)進行作圖,由圖5(a)可知:在同一參數下,不同初始狀態的分叉圖也存在著差異,且無論是紅色或是藍色均在b=11右側出現斷層現象。將藍色狀態下的分叉圖剝離開來,觀察到藍色初值狀態下的參數b→11的時候出現明顯的分叉斷層現象,如圖5(b)所示。

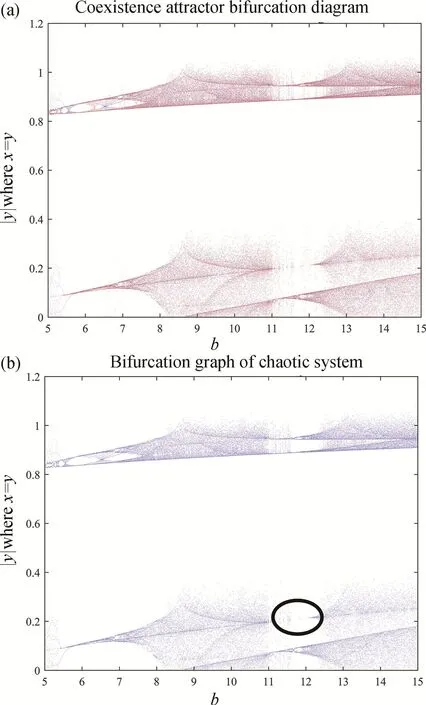
圖5 分叉圖。(a)不同初始值狀態;(b)單一初始值狀態Fig.5 Bifurcation diagram.(a)Different initial value state;(b)Single initial value state

在傳統的混沌分叉區域分析中,混沌分叉會呈現周期分叉,伴隨著混沌軌道呈現周期現象,此時系統不混沌。系統(1)的分叉不僅具有周期性、雙層分叉性,而且出現了其他系統沒有的分叉斷層區域,分叉斷層意味著混沌周期性消失,此時系統不再具有混沌特性,藍色分叉圖在區間b=[11,12]出現類周期現象,具有4個類周期窗口,且在第三個類周期窗口出現分叉斷層(圖5(b)黑色橢圓區域),因此判斷分叉斷層區可能會對混沌系統產生影響,為此本文從該區域的Lyapunov指數譜圖6(a)和最大Lyapunov指數圖6(b)進行探究。

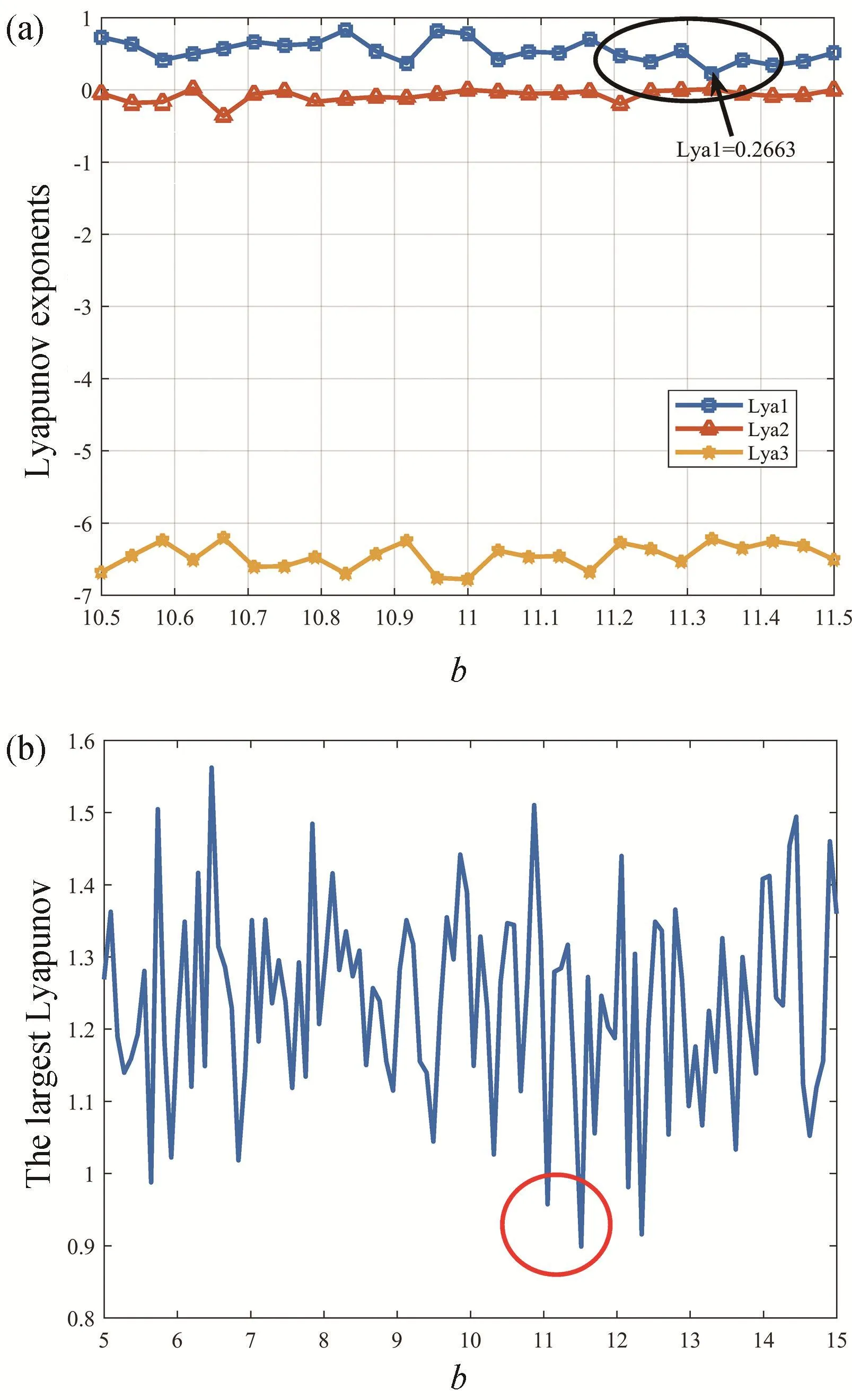
圖6 Lyapunov指數。(a)Lyapunov指數譜;(b)最大Lyapunov指數Fig.6 Lyapunov index.(a)Lyapunov index spectrum;(b)Maximum Lyapunov index

設定參數b的范圍為 [10.5,11.5],步長為0.05,從圖6(a)的Lyapunov指數譜可以看出在參數b=11,正的Lyapunov出現急劇下降,且在b=11.34左右達到最低點,此時Lyapunov=0.2663。為了更好地體現分叉斷層區Lyapunov指數的變化狀況,采用奇異值分解法來求解該區域系統的最大Lyapunov指數,如圖6(b)可以反映出參數b=11時,系統的最大Lyapunov指數急劇下降的現象更加明顯,且持續時間較長,與參數在b=[5,6]時的混沌類周期窗口相似,由于此區域還有別的類周期窗口,混沌軌道不會出現周期性變換,更不會出現相近軌道最終會靠攏合并為一點,但是此時系統的Lyapunov指數減小,混沌特性不夠明顯,混沌程度也會減小。因此可以得出一個結論:當混沌系統出現單一分叉斷層時,多層分叉或者類周期窗口可以保證系統的混沌特性。

1.4 混沌圖和復雜度分析

由于該憶阻混沌系統存在分叉斷層行為,且最大Lyapunov指數急劇下降,那么找出該系統的最優參數范圍顯得尤為重要。采用雙參數影響下的混沌圖和復雜度分析相結合的方法來選取混沌系統的最優參數范圍。混沌圖是在參數空間中反映混沌系統動力學的一種綜合方法,系統的參數應該選擇在復雜度較高的區域;測量復雜度的方法有頻譜熵(SE)、C0熵和排列熵(PE)[21-23]。其中,PE算法是準確、快速估計數值序列的正確選擇。因此,采用排列熵(PE)算法分析了在b參數范圍下混沌系統的復雜性,PE值越大,時間序列越復雜。

從圖7(a)雙參數影響下的混沌圖可知:系統參數b∈(7.5,11)、a∈(0.4,1.1)區間的混沌信號的復雜度幾乎接近1,基本符合參數b范圍下的混沌復雜度分析,系統參數在此范圍下可以達到最優,此時,混沌信號的隨機性更強,更適用于安全通訊領域。

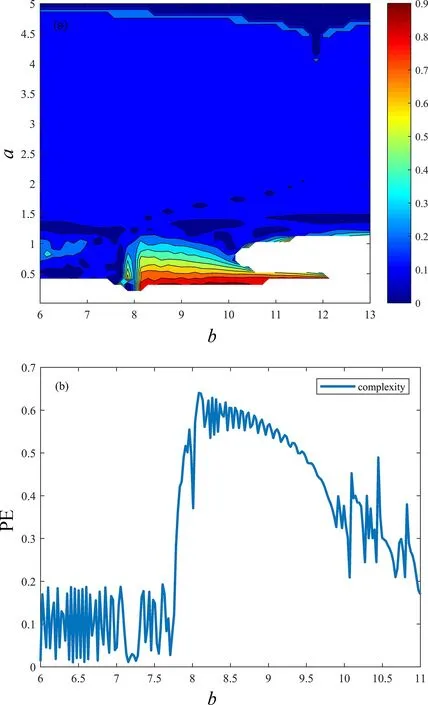
圖7 最優憶阻混沌系統參數。(a)混沌圖;(b)PE復雜度分析Fig.7 Parameters of optimal memory chaotic system.(a)Chaotic diagram;(b)PE complexity analysis

1.5 最優參數范圍下的多穩態共存分析

多穩態是指系統擁有的不同穩定運行狀態,且會隨著時間在兩個或幾個互斥的狀態之間切換,在混沌系統中有大量不同軌跡共存的特殊形式,多穩態系統很容易受初始條件的影響。表1提供了不同初始狀態下系統多穩態共存的參數。

在最優參數范圍下系統存在多穩態共存現象,給定系統(1)的參數,分別設定系統的初始狀態,時間為5 s,如圖8(a)顯示:初始狀態(u1,v1,w1)為藍色軌道,(u'1,v'1,w'1)為紅色軌道,此時混沌的吸引域形成,且系統出現多穩態共存現象。設置時間為15 s,如圖8(b)顯示:初始狀態(u1,v1,w1)為紅色軌道,(u'1,v'1,w'1)為藍色軌道,此時兩個雙渦卷憶阻混沌系統軌道會出現指數級分離,紅色軌道主要聚集在左渦卷區域,藍色軌道在左右渦卷吸引域產生聚集,系統的多穩態共存現象更加顯著。

圖8 v-w平面的多穩態共存。(a)t=5 s;(b)t=15 sFig.8 Coexistence of multiple steady states in v-w plane.(a)t=5 s;(b)t=15 s

從上述系統的多穩態現象可以反映出,系統在最優參數范圍控制下,隨著迭代次數的增加,系統的多穩態共存現象也更加明顯,表明在最優參數范圍控制下,該憶阻混沌系統具有豐富的動力學行為。

表1 多穩態共存參數Tab.1 Multi-steady-state coexistence parameters

2 基于Multisim的憶阻混沌電路實現

Multisim提煉了SPICE仿真的復雜內容,并對電路進行捕獲、仿真和分析新的設計,通過Multisim和虛擬儀器技術,可以完成從理論到原理圖捕獲與仿真,再到原型設計和測試這樣一個完整的綜合設計流程。除此之外,虛擬的模擬元器件容易受到環境的溫度、濕度以及元件器老化等條件的約束,Multisim具有豐富的元器件來提供電路的配置。由于文中的憶阻器中含有開方運算,因此要采用改進的電路模塊化設計方案[24],使用Multisim14.0版本搭建憶阻混沌系統的電路。

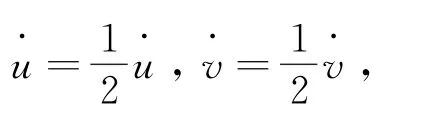
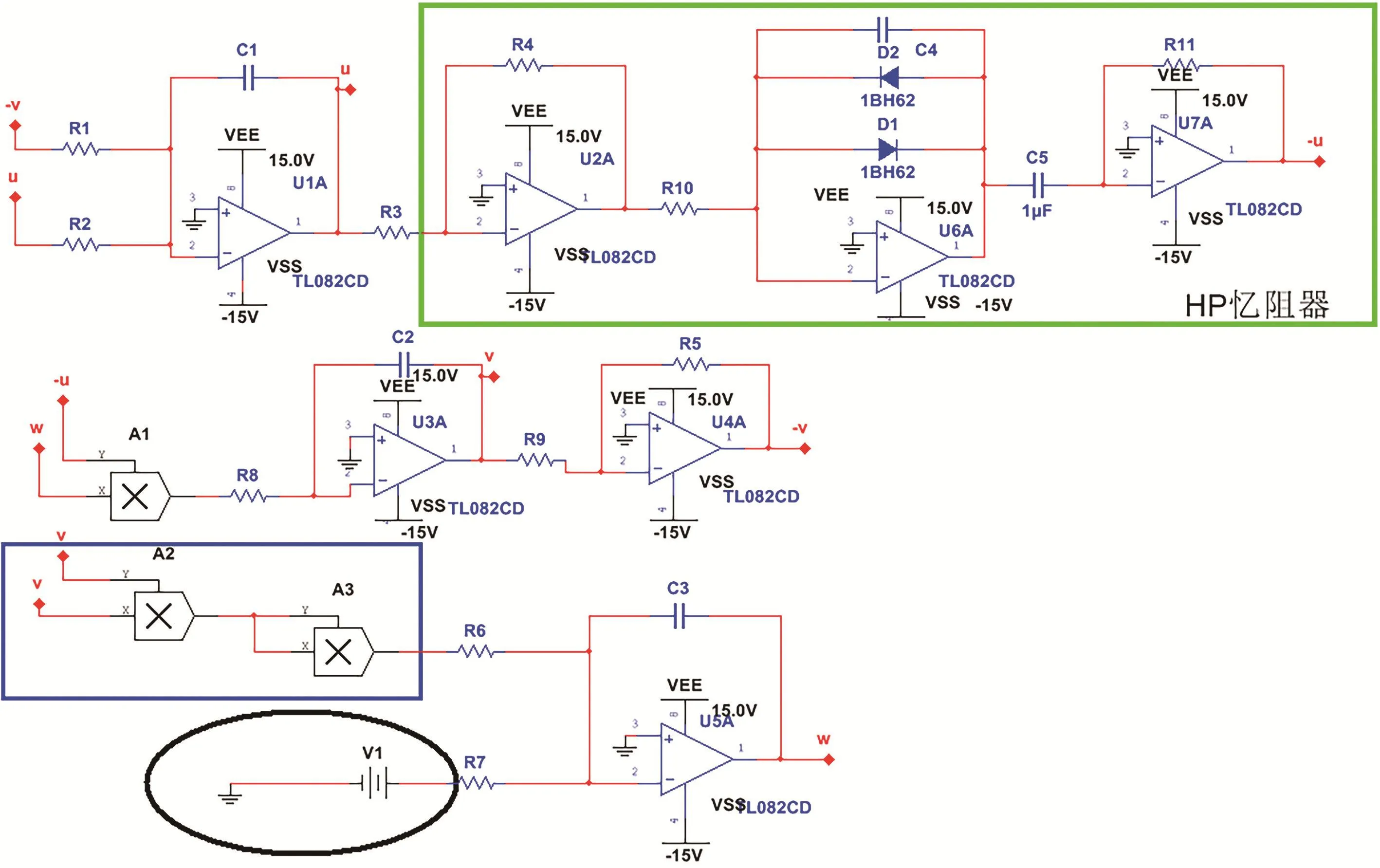
圖9 磁控二氧化鈦憶阻混沌電路原理圖Fig.9 Schematic diagram of a new double vortex memristor chaotic circuit

其狀態方程為:

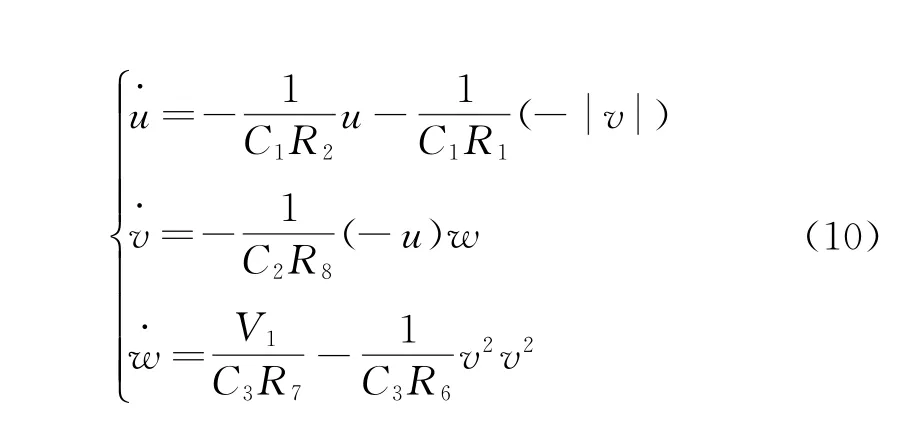
在圖9中,R1,R2的電阻值為66.67 kΩ,R3,R4,R5,R6,R8,R9的電阻值為100 kΩ,R7的電阻值為32 kΩ,C1=C2=C3=1μF,電源元器件V1=-1 V,對于含有憶阻器模塊,元器件R10=16 kΩ,C4=10μF,C5=10 nF,R11=10 kΩ,電路中采用模擬乘法器Multiplier,運算放大器采用TL082CD,電源電壓為±15 V,從而實現系統中非線性乘積項的乘法運算。藍色框采用雙乘法器模擬v2v2中的雙乘法運算,黑色橢圓區域采用負電壓反向控制模擬常數項,綠線框內為構造的磁控二氧化鈦憶阻器。圖10為系統(1)的電路仿真結果。示波器顯示的仿真結果與數值仿真的結果一致,驗證了該憶阻混沌系統在物理上實現的可能性。

3 結論

由于憶阻器尺寸較小、能耗低,在混沌電路中有著較高的應用價值,本文將磁控二氧化鈦憶阻器作為混沌系統的非線性項,提出了一種基于磁控二氧化鈦的新型雙渦卷憶阻混沌系統,詳細地分析了系統的復雜動力學行為,設計了該憶阻混沌系統的模擬電路,并進行了仿真,得出如下結論:

(1)該憶阻混沌系統出現分叉斷層現象或者類周期性窗口時,系統的雙分叉可以保證系統的混沌特性,但是此時的Lyapunov指數會急劇減小,系統的混沌特性會降低。

(2)采用雙參數影響下的混沌圖和復雜度分析結合的方法,可以得到分叉斷層區間系統的最優參數。

(3)在最優參數范圍下的憶阻混沌系統,系統多穩態共存現象顯著,具有豐富的動力學行為。

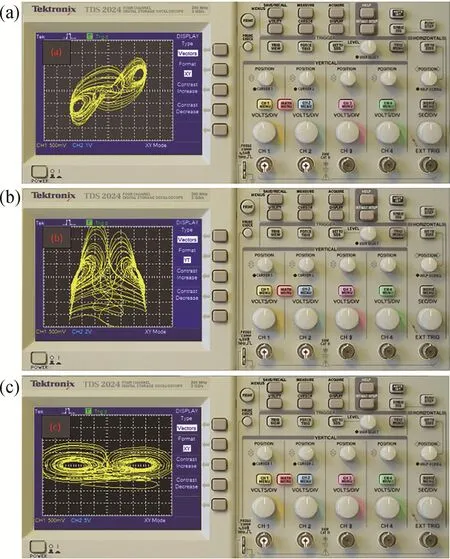
圖10 示波器顯示系統(1)的相圖。(a)u-v平面;(b)u-w平面;(c)v-w平面Fig.10 Phase diagram of oscilloscope display system.(a)u-v plane;(b)u-w plane;(c)v-w plane