CdS晶體電子自旋相干動力學

郭家興,吳 真,梁 盼,姜美珍,胡蓉蓉,3,張圓圓,馮東海

（1. 華東師范大學 精密光譜科學與技術國家重點實驗室, 上海 200241; 2. 上海電機學院 文理學院,上海 201306; 3. 上海應用技術大學 理學院, 上海 200235）

0 引 言

利用半導體中的電子自旋特性來實現自旋電子器件已成為半導體行業中的研究熱點[1-2]. 電子自旋向上和自旋向下兩個態的相干疊加構成一個量子比特, 而量子比特又是量子信息處理的基本物理單元[3]. 伴隨著當今量子計算機的蓬勃發展, 半導體中的自旋相干特性又再一次映入眼簾, 尋找合適的量子信息處理載體成為重中之重.

對于塊體半導體材料, 現已有各種關于電子自旋相干動力學的研究成果. 例如, III-V族n-GaAs塊體材料[4]和本征GaAs塊體材料[5-8]的電子自旋動力學隨溫度(T)、光激發電子密度、激發光能量的依賴性得到了廣泛研究; 在III-V族GaN體系中, 發現磁場和溫度可以有效地影響n-GaN外延層薄膜中的電子自旋相干動力學[9];T= 293 ～ 500 K的較高溫度下, n-GaN的自旋相干動力學的研究[10]等等. 此外, 在II-VI族化合物半導體中, 具有較小自旋軌道耦合能的直接帶隙半導體ZnO得到了廣泛的關注, 電子密度、磁場、溫度、熱處理對其電子自旋相干性的影響都獲得了深入研究[11-12]. 含鎘硫屬化合物CdTe同樣也有較多的研究. 例如, Sprinzl等[13]研究了電子濃度和溫度對n-CdTe電子自旋相干動力學的影響,T= 7 K時, 在最佳摻雜濃度樣品中發現2.5 ns的自旋退相位時間; Ma等[14]研究了CdTe自旋動力學中的激發光子能與載流子密度對自旋弛豫時間的影響; Ito等[15]從理論上研究了CdTe中的電子g因子的溫度依賴; Kimel等[16]在室溫下發現了CdTe自旋動力學有兩種弛豫過程.

纖鋅礦CdS作為II-VI族鎘硫屬化合物半導體之一, 具有獨特的電子和光學特性, 在太陽能轉換、非線性光學、光電子、光催化領域已經具有重要應用. 相比于同族化合物CdTe (?so=800 MeV)[14],CdS具有較小的自旋軌道分裂能 (?so=65 MeV)[17], 因此從理論上來講, 它會具有更長的自旋退相干時間. 但是在自旋電子學領域, 國內外對CdS塊體半導體的研究還很少, 目前的研究主要集中在CdS半導體量子點體系. 例如, 馮東海等[18-21]發現CdS量子點在室溫下具有長達3 ns的自旋退相位時間、表面態對自旋具有重要影響等特性; 而對塊體CdS體系僅僅只有初步的研究[22]. 考慮到各種III-V族和II-VI族塊體半導體有豐富的自旋現象, 以及為了更好地認識CdS低維半導體的自旋特性, 有必要對CdS塊體半導體的自旋動力學進行深入的研究.

本文主要利用研究電子自旋動力學的常用技術—時間分辨克爾旋轉(TRKR)光譜法深入研究了n-CdS單晶在不同溫度、不同波長條件下的自旋相干動力學. 纖鋅礦CdS晶體在 Γ 點(波失k=0)的能帶結構圖如圖1a)所示, 其中, CB為導帶（conduction band), HH為重空穴價帶(heavy hole valence band), LH (light hole valence band)為輕空穴價帶, SO為自旋軌道耦合價帶(spin orbit coupled valence band). 晶格場分裂和自旋軌道耦合分裂使其價帶分裂為重空穴價帶A、輕空穴價帶B和自旋軌道耦合價帶C, 帶間參數詳見圖1a). CdS晶體在圓偏振光作用下, 建立自旋極化. 圖1b)為左旋圓偏振光σ?(虛線)和右旋圓偏振光σ+(實線)作用下帶邊重空穴激子(A激子)和輕空穴激子(B激子)的光學躍遷選擇定則.

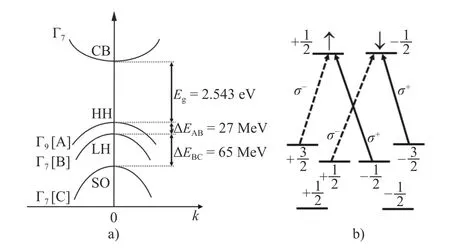
圖1 a)纖鋅礦CdS的能帶結構和b)光學選擇定則Fig. 1 a) Band structure and b) optical selection rules for wurtzite CdS

1 實驗描述

1.1 樣 品

實驗所使用的樣品為n-CdS單晶, 購買于美國MTI公司. 其晶體結構為6方纖鋅礦結構, 晶向為〈0001〉; 電阻小于1 ohm/cm, 電子密度為1017cm–3; 晶體雙面拋光, 尺寸為10 mm× 10 mm ×1 mm.

1.2 實驗方法

使用時間分辨克爾旋轉(TRKR)光譜法來探測CdS單晶的自旋動力學. 具體實驗裝置如圖2所示,由飛秒激光放大器(fs laser)、光參量放大器OPA(Optical Parameter Amplification)、BBO(β-Ba(BO2)2)晶體、凸透鏡(L)、 平面高反鏡(M)、 分束片(BS)、 格蘭激光偏振片(G-L)、 1/4波片(λ/4)、1/2波片(λ/2)、電光調制器EOM(Electro-Optic Modulator)、延遲線(Delay line)、 沃拉斯頓棱鏡(Wollaston prism)、電磁鐵(Magnet)、鎖相放大器(Lock in)、平衡光電探測器(Balanced photodetector)、計算機(PC)等組成. CdS晶體放置在低溫恒溫器樣品腔中, 樣品溫度在5 ～ 300 K范圍內可調. 腔體放置在電磁鐵中間, 由電磁鐵提供恒定的橫向磁場. 本實驗所用的磁場(B)固定在1 T.

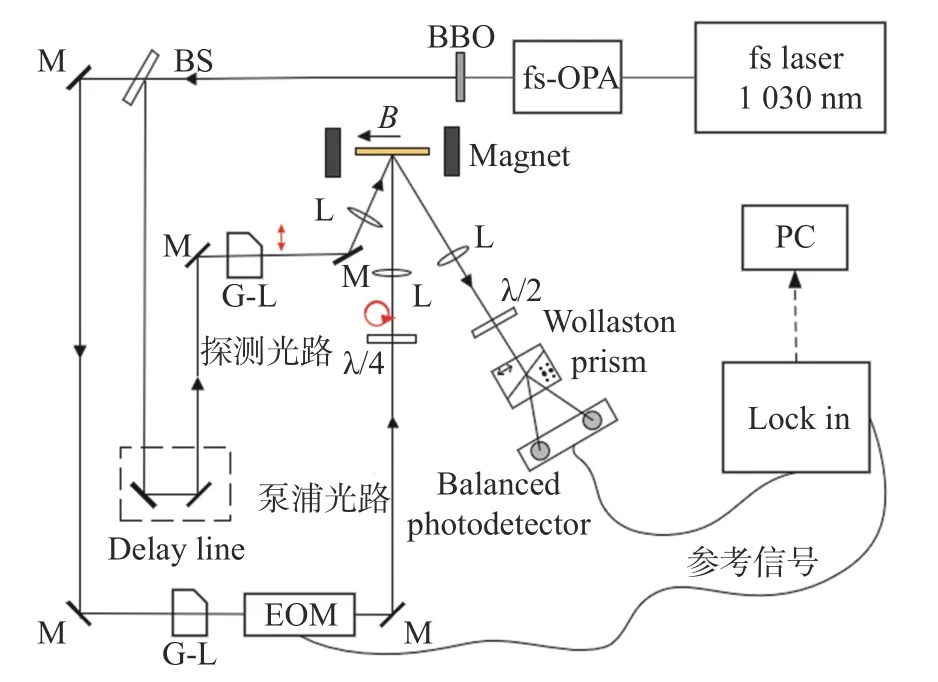
圖2 時間分辨克爾旋轉實驗裝置示意圖Fig. 2 Schematic diagram of experimental device for time-resolved Kerr rotation measurements

該實驗裝置所需的光源是1臺Light Conversion飛秒激光放大器(中心波長為1 030 nm, 最大輸出功率為20 W, 重復頻率為50 kHz). 飛秒激光放大器出射的高功率脈沖光經過OPA(其出射光波段范圍為630 ～ 2 600 nm)以及BBO晶體倍頻后, 獲得脈寬為200 fs、線寬為2.5 nm、波長在CdS帶隙附近的輸出脈沖. 激光脈沖經過整平行處理后, 被偏振分束片分成兩束光脈沖, 一束作為泵浦光脈沖,另一束作為探測光脈沖, 且兩束光脈沖的功率比為7∶3. 泵浦光脈沖首先經過格蘭激光偏振片獲得垂直方向激光偏振, 然后再經過EOM獲得垂直和水平方向上的偏振調制, 調制頻率為20 kHz. 線偏振調制的激光經過1/4波片后獲得左旋和右旋間的圓偏振調制, 最后通過凸透鏡聚焦垂直入射到樣品上, 焦斑直徑大約為200 μm. 探測光脈沖通過機械延遲線調節其與泵浦光脈沖之間的時間延遲, 再經過格蘭激光偏振片獲得線偏振光脈沖, 最后通過凸透鏡聚焦以小角度斜入射到樣品上. 探測光脈沖和泵浦光脈沖均通過中性密度濾波片調整光功率. 實驗要求最終入射到樣品上的泵浦光和探測光功率比為10∶1.

探測光斜入射到樣品上的反射光通過凸透鏡匯聚并由1/2波片、沃拉斯頓棱鏡、平衡光電探測器等器件組成的光平衡橋探測系統接收, 并將信號輸入到鎖相放大器, 最終得到自旋動力學信息. 調整好光功率并將兩束光聚焦在樣品上的同一點. 正式測量數據之前, 首先擋住泵浦光, 調整光平衡橋系統里的1/2波片的光軸方向, 使平衡光電探測器兩個探頭接收到的光功率相同; 之后放開泵浦光, 平衡光電探測器輸出信號的演化即代表了自旋信號的演化.

在光致發光譜的測量中, 激發光為連續光, 由1臺360 nm的固體紫外激光器提供, 發光譜由S2000光纖光譜儀采集獲得.

2 實驗結果與討論

CdS晶體在圓偏振光作用下建立自旋極化, 自旋極化電子繞著外加橫向磁場做拉莫爾進動. 圖3所示為T= 5 K條件下CdS單晶的自旋動力學隨波長的依賴, 其中, 圖3a)為較長泵浦探測波長(Pump-probe delay)(490.7 nm以上)下獲得的自旋動力學, 圖3b)為較短泵浦探測波長下(489.8 nm以下)獲得的自旋動力學. 在較長波長下, 自旋相干信號可持續到7.5 ns以上; 而在較短波長下, 自旋相干信號在0.25 ns時已消失. 從圖3a)和3b)可看到, 隨著泵浦探測波長的改變, CdS的自旋動力學明顯分成兩個區間, 即短壽命和長壽命區間. 當激發波長為490.7 nm時, 在TRKR光譜中可以同時看到短壽命自旋信號和長壽命自旋信號(圖3a)中的黑色曲線以及圖3c)中的藍色曲線). 短壽命與長壽命具有不同的旋進頻率, 導致其疊加信號出現幅度上的調制. 當激光波長從488.2 nm增大到490.7 nm時, 在自旋信號中可以明顯的觀察到相位翻轉的現象, 如圖3c)所示.

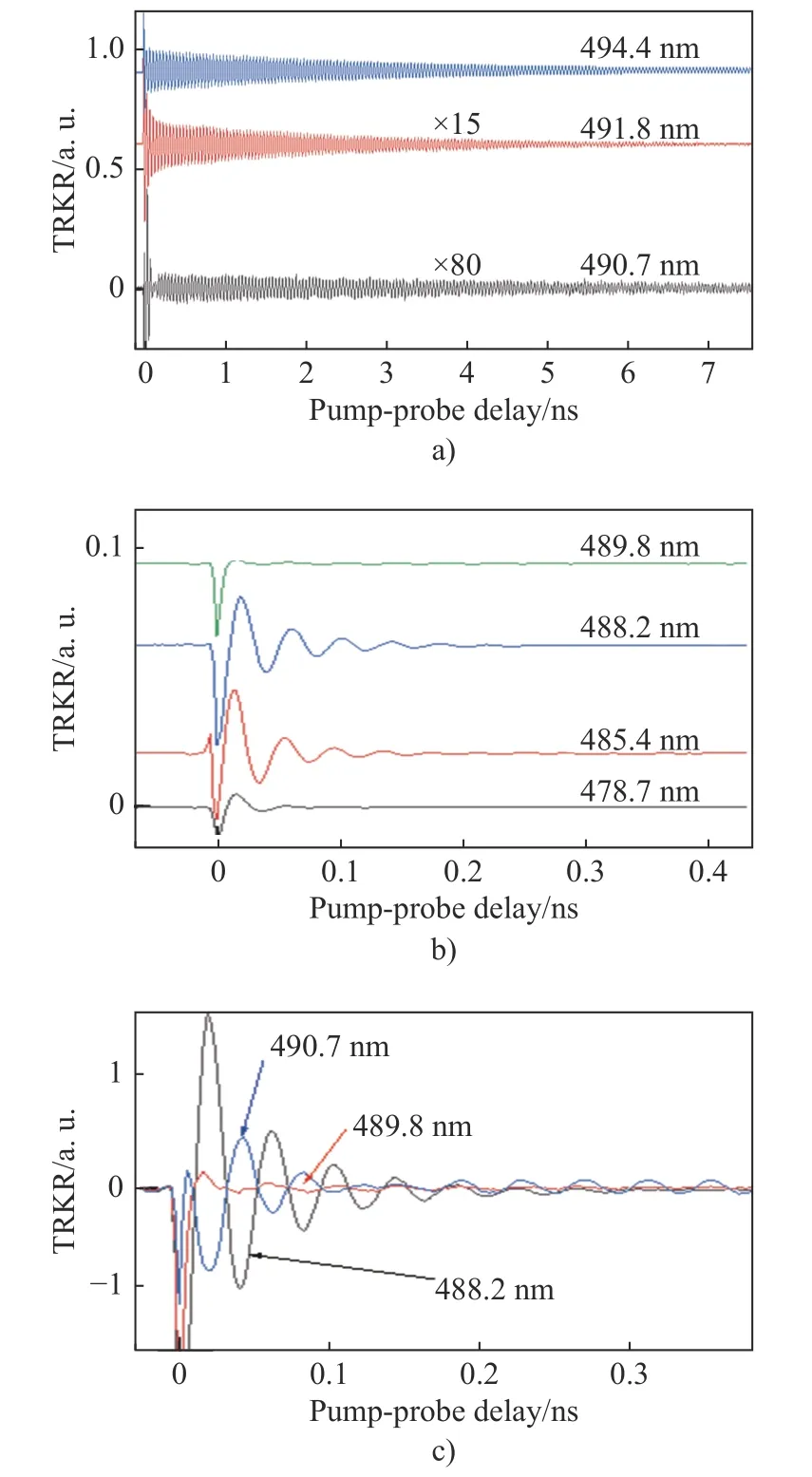
圖3 T = 5 K, B = 1 T時, CdS單晶在不同波長下的時間分辨克爾旋轉光譜:a)為長壽命自旋信號; b)為短壽命自旋信號; c)相位翻轉示意圖Fig. 3 TRKR measurements in a CdS single crystal at different wavelengths for T = 5 K and B = 1 T:a) Long-lived spin signal; b) Short-lived spin signal; c) Phase inversion schematic diagram

激光波長改變導致自旋信號相位翻轉現象在TRKR光譜中很常見. 實驗中泵浦探測波長是簡并的, 掃波長的同時泵浦探測波長均在變化, 因此相位翻轉可能是探測光改變而引起的, 也可能是激發光改變而引起的. 自旋極化電子導致探測光的σ+和σ?分量的復折射率不同, 從而產生克爾旋轉信號.折射率差值的大小以及正負號會隨著探測光波長的改變而改變, 在共振能級附近出現相位翻轉[4,23-24].此外, 同種圓偏振激發光作用下, 重空穴激子與輕空穴激子中的電子自旋方向相反(如圖1b)所示),所以激發光能量從小變大的過程中, 也可能會導致自旋信號相位翻轉[6]. 如果是激發光的改變而導致相位翻轉, 那么這個位置理論上應該在A激子(487.7 nm, 對應發光峰)與B激子(482.5 nm, 因為晶體場分裂能是 ～ 27 MeV)之間且偏向于B激子的位置(因為B激子的產生幾率更低). 然而圖3c)中相位翻轉位置在發光峰波長之上, 因此該現象是由探測光變化所導致的.

圖3c)實驗所用激光線寬為2.5 nm, 而489.8 nm和490.7 nm僅相差0.9 nm, 卻有明顯不同的自旋信號. 為了說明這一現象, 本文理論模擬了克爾旋轉信號(Kerr rotation,K)隨波長(Wavelength)的依賴, 并分析了寬譜探測對結果的影響, 詳見圖4. 克爾旋轉信號K可以表示為[25]

其中,F為法拉第旋轉信號,E為橢偏信號,為探測光中心角頻率,εr為相對介電常數,c為光速),L可視作光穿透深度. 法拉第旋轉信號和橢偏信號均為透射方向上所探測的信號: 前者對應自旋極化體系下左旋圓偏振探測光和右旋圓偏振探測光的折射率不同所導致; 后者由于兩圓偏振探測光的吸收不同所導致. 本文實驗中探測光為線偏振, 可視為左旋圓偏振光和右旋圓偏振光的組合.材料折射率, 吸收系數, 復介電常數ε(ω) 具有表達式[23]

其中,εb是本底介電常數,f是振子強度,ω0為激子共振頻率,γ是為激子阻尼率. 由于相空間填充導致的飽和效應, 自旋極化體系下左旋和右旋圓偏振探測光的振子強度f將有所區別.

圖4a)中黑色虛線為根據公式(2)所獲得的理論克爾旋轉信號(窄帶寬探測), 所用的各參數值分別為,εr=6,L=200 nm,ω0=2.532 eV, 對應489.8 nm波長,γ=10 MeV, 由CdS單晶在5 K溫度下的熒光線寬估計所得. 注意公式(2)的分式項相對于εb是個小量, 在此前提下,εb和f的取值對所模擬的克爾信號隨波長的相對依賴關系沒有影響. 由于本文實驗用的激光線寬為2.5 nm, 故需要對圖4a)的模擬結果(黑色虛線)進行修正. 假設激光為高斯線型, 有

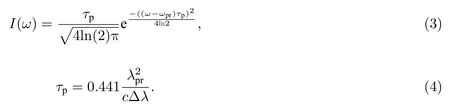
公式(1)與公式(3)相乘并積分即得到寬帶寬探測脈沖下( ?λ=2.5 nm)的克爾旋轉信號Kbroad(如圖4a)中的紅色實線所示). 可以看出, 相比于窄帶寬探測, 寬帶寬探測所獲得的克爾旋轉譜峰值會有所移動, 峰值信號也會降低, 但總體趨勢類似: 同樣存在明顯的相位翻轉現象. 圖4a)標記了489.8 nm、490.7 nm和488.2 nm在寬譜探測光譜中所處的位置. 489.8 nm的Kbroad為0; 490.7 nm的Kbroad為負值; 488.2 nm的Kbroad為正值, 但其比490.7 nm的信號幅度要大. 該模擬結果與圖3c)的實驗結果基本吻合. 為了更形象地說明, 圖4b)、圖4c)、圖4d)分別模擬了中心波長為489.8 nm、490.7 nm和488.2 nm高斯譜線上各位置點所對應的克爾旋轉信號, 即窄帶寬探測克爾旋轉信號 (圖4a)中黑色虛線)與公式(3)相乘但不積分時的結果. 如圖4b)所示, 對于489.8 nm高斯脈沖(2.5 nm線寬), 中心波長489.8 nm的克爾旋轉信號為0, 小于489.8 nm和大于489.8 nm的信號對稱, 但一正一負, 所以對整個波長積分后的總信號仍為0. 如圖4c)所示, 對于490.7 nm高斯脈沖(2.5 nm線寬), 同樣小于489.8 nm的克爾旋轉信號為正, 大于489.8 nm的信號為負, 但整個波長范圍負信號幅度遠大于正信號幅度, 所以對整個波長積分后的總信號為負值. 同樣, 對于488.2 nm高斯脈沖(2.5 nm線寬), 整個波長范圍正信號幅度遠大于負信號幅度, 所以對整個波長積分后的總信號為正值. 積分后的總信號即對應圖4a)中的紅色實線上所對應的3個點. 由此解釋了圖3c)中的實驗結果是合理的.

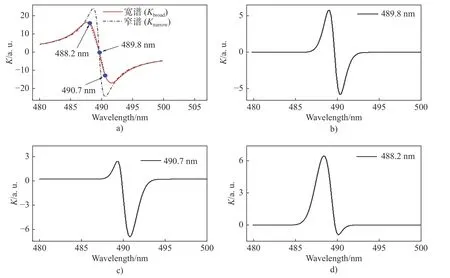
圖4 克爾旋轉信號理論模擬: a)窄譜(黑色虛線)和寬譜(紅色實線)探測的克爾旋轉信號振幅隨波長的依賴性對比; 中心波長分別為 b) 489.8 nm、c) 490.7 nm和 d) 488.2 nm高斯譜線上各位置點所對應的克爾旋轉信號Fig. 4 Theoretical simulation of Kerr rotation signal: a) Comparison of the spectral dependence of Kerr rotation under the narrowband detection pulse (black dotted line) versus the broadband detection pulse (solid red line);Kerr rotation signal corresponding to each point on the Gaussian spectral line with a center wavelength of b) 489.8 nm, c) 490.7 nm, and d) 488.2 nm

自旋極化體系與周圍環境的相互作用會導致自旋弛豫, 從而使得自旋信號由于拉莫爾進動做周期性振蕩的同時, 其振幅隨著延遲時間呈指數衰減. 自旋信號隨時間的演化公式為

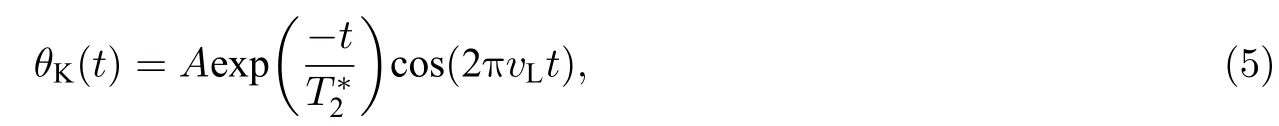
其中,A為圓偏振泵浦光在CdS單晶中建立的初始自旋極化所對應的克爾旋轉幅度;t為延遲時間;為自旋退相位時間;vL為拉莫爾進動頻率, 也即圖3a)中自旋信號的振蕩頻率. 拉莫爾進動頻率vL=gμBBext/h, 其中g為朗德因子,μB為玻爾磁子,Bext為外加橫向磁場大小,h為普朗克常數. 根據式(5), 將圖3中各種波長下的TRKR譜線進行擬合, 并將擬合的自旋退相位時間隨波長依賴結果整理到圖5a)中. 從圖5a)中可以看出, 短壽命(Short)自旋信號的自旋退相位時間在40 ps左右;而長壽命(Long)自旋信號的自旋退相位時間在納秒量級, 且隨激發波長的增大而增大, 在508 nm附近長達 4.8 ns.

本文對探測到的不同波長下的TRKR動力學曲線進行了快速傅里葉變換(Fast Fourier Transform, FFT), 所獲得的頻率峰值隨波長的依賴關系如圖5b)所示. 從圖5b)可以看出, 短壽命自旋信號的vL與長壽命自旋信號的vL存在明顯的差異, 短壽命自旋信號的vL普遍大于長壽命自旋信號的vL. 在測量波長范圍內, 長壽命自旋信號的vL不隨波長變化, 恒定為vL=23.807 GHz ; 而短壽命的進動頻率在不同波長處具有不同的值.

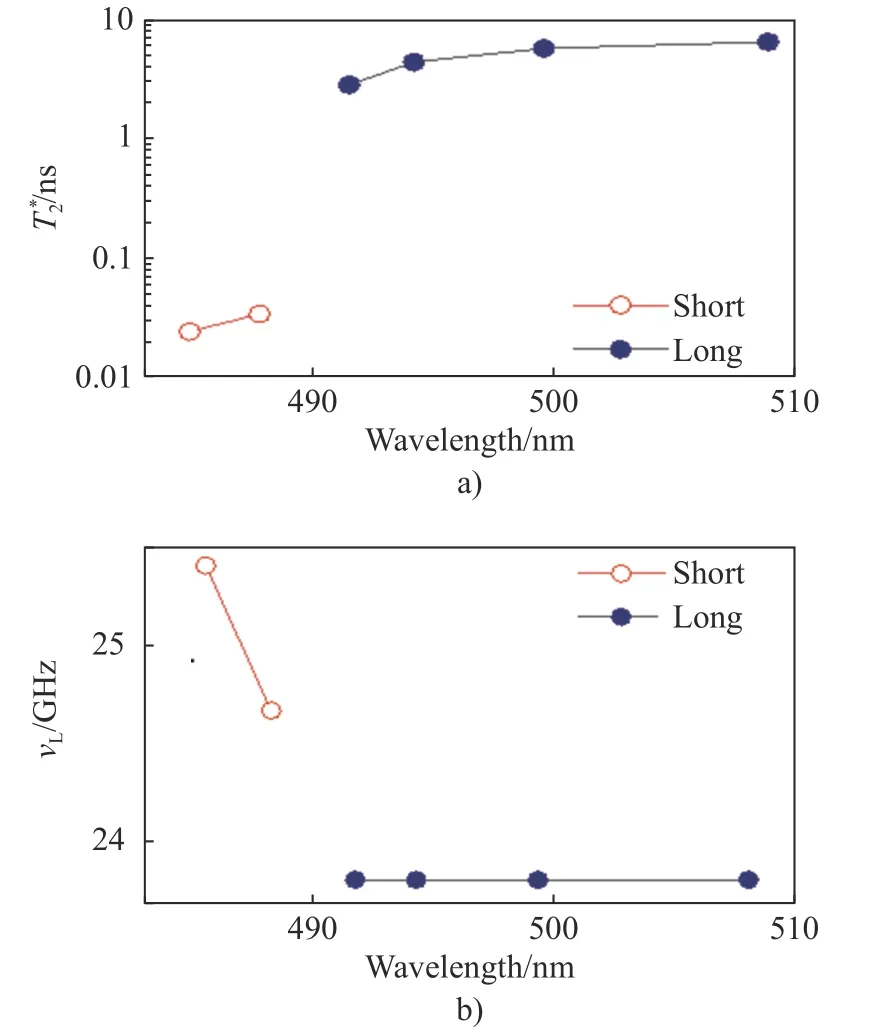
圖5 T = 5 K條件下, a)自旋退相位時間 和b)拉莫爾進動頻率 vL 隨波長的依賴Fig. 5 Wavelength dependence of a) spin-dephasing time and b) Larmor precession frequency vL atT=5 K

圖6a)、圖6b)為T= 50 K條件下CdS單晶自旋動力學隨波長的依賴. 從圖6a)、圖6b)中可以看出, 隨著泵浦探測波長的改變, CdS的自旋動力學仍分為短壽命和長壽命兩個區間. 當激光波長為491.8 nm時, TRKR光譜中可以同時看到短壽命自旋信號和長壽命自旋信號, 見圖6a)中的紅色曲線.圖6b)中, 當激發波長從488.3 nm增大到491.1 nm時, 短壽命自旋信號中出現類似于T= 5 K條件下的相位翻轉現象, 且翻轉位置在發光峰波長(488.41 nm)之上. 根據式(5)將各波長下的TRKR信號進行擬合, 并將隨波長的依賴結果整理到圖6c)中. 從圖6c)中可看出, 短壽命自旋信號的仍為30 ～ 40 ps左右, 與T= 5 K時的值幾乎一致; 但長壽命自旋信號的變為幾百皮秒量級, 在508 nm附近為425 ps, 比T= 5 K時的值(4.8 ns)小了一個數量級. 圖6d)為拉莫爾進動頻率vL隨波長的依賴關系, 短壽命自旋信號的vL仍普遍大于長壽命自旋信號的vL, 在不同波長處有不同的值; 長壽命自旋信號的vL恒定不變, 仍為23.807 GHz, 即與T=5 K時的值一致.

圖7a)為T= 293 K條件下CdS單晶自旋動力學隨波長的依賴, 此時隨著泵浦探測波長的改變,僅能看到短壽命自旋信號信息, 但相位翻轉現象仍然存在, 且翻轉位置仍在發光峰波長(505 nm)之上. 圖7b)是293 K時自旋退相位時間隨波長的依賴. 從圖7b)中可以看出,仍為幾十皮秒量級, 隨激發波長增加而有所增大.

為深入探究溫度(T)對自旋退相位時間的影響, 本文將T= 5 K、T= 50 K、T= 293 K這3個溫度下的自旋退相位時間隨波長的依賴關系整理到了圖8a)中. 從圖8a)中可以看出, 長壽命自旋信號的隨著溫度的升高整體減小, 短壽命自旋信號的隨溫度變化不明顯. 圖8b)表示泵浦探測波長在發光峰時, 自旋退相位時間和拉莫爾進動頻率vL隨溫度的依賴關系, 在發光峰波長處,僅存在短壽命自旋信號. 從圖8b)可看出, 改變溫度對短壽命的和vL影響不大. 在溫度5 K到293 K這段區間, 發光峰隨溫度的升高而增大, 見圖8b)中的插圖. 這是因為溫度升高會導致CdS單晶的帶隙變窄; 但始終保持在40 ps左右, 而vL在25 GHz左右.

圖6 T = 50 K, B = 1 T時: a)、b)不同波長下的時間分辨克爾旋轉光譜;c)自旋退相位時間隨波長的依賴; d)拉莫爾進動頻率 vL 隨波長的依賴Fig. 6 a), b) TRKR signals at different wavelengths; c) Dependence of the spin dephasing time, on wavelength;(d) Dependence of the Larmor precession frequency,vL on wavelength; Where T = 50 K, B = 1 T

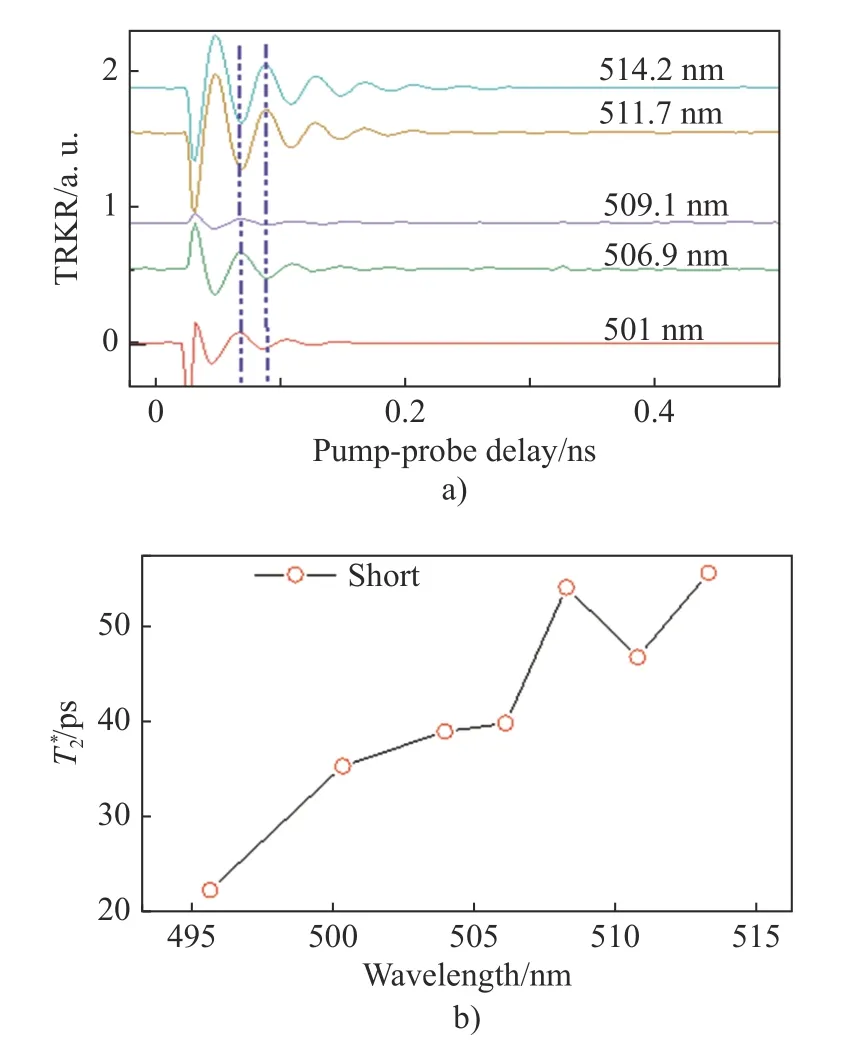
圖7 T = 293 K, B = 1 T時, a)不同波長下的時間分辨克爾旋轉信號和 b)自旋退相位時間 隨波長的依賴Fig. 7 a) TRKR signals at different wavelengths; b) Dependence of spin dephasing time,on wavelength; Where T = 293 K and B = 1 T

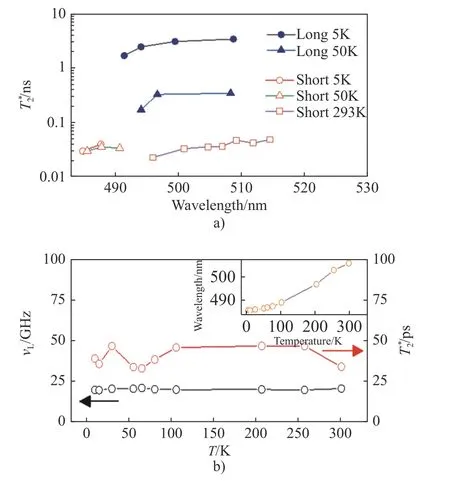
圖8 a)不同溫度下自旋退相位時間隨波長的依賴關系; b)發光峰處波長激發的自旋信號退相位時間 、拉莫爾進動頻率 vL 隨溫度的依賴關系, 插圖為發光波長隨溫度的依賴Fig. 8 a) Wavelength dependence of spin dephasing time, , at different temperatures; b) Temperature dependence of the spin dephasing time, , and Larmor precession frequency,vL, at the emission peak wavelength, inset shows the emission peak as a function of temperature

在n-CdS半導體中存在著兩類電子: 一類是導帶中的自由電子; 另一類是雜質缺陷所導致的局域電子. 根據自旋動力學隨溫度的依賴關系, 可以判定短壽命自旋信號來自于導帶中的自由電子, 而長壽命自旋信號來自于局域電子. 在n型摻雜半導體中, 低溫下局域電子和導帶自由電子同時存在. 隨著溫度的升高, 局域電子逐漸退局域而轉變成自由電子. 例如, 在電子濃度為1016cm–3的n-GaAs中,T> 50 K時, 局域電子會消失, 導帶自由電子占主導地位[26]. 對于本文實驗中所使用的n-CdS單晶,T=60 K時已看不到長壽命自旋信號. 由于相空間效應, 局域電子的自旋退相位時間比導帶自由電子的更長[26]. 局域電子隨溫度的升高而減小, 原因在于鄰近自旋之間的各向異性Dzyaloshinsky-Moriya 相互作用. 由于自旋進動中聲子的波動, 這種自旋相互作用會隨著溫度的升高而增加, 從而導致長壽命自旋退相位時間隨著溫度T的增大而不斷衰減[26-27]. 低溫條件下局域電子隨波長減小而減小, 見圖5a)和圖6 c). 這是因為激光波長逐漸減小會導致局域態和導帶中的流動態不斷混合, 從而使得不斷減小[4].

自由電子短壽命自旋信號的自旋退相位時間隨溫度基本不變, 類似的現象在GaN晶體中已有報道, 原因在于電子高度簡并狀態下的D’yakonov–Perel’(DP)弛豫機制[28-29]. DP弛豫機制基于自旋軌道耦合所引起的本征導帶自旋分裂, 自旋軌道耦合會誘導出一個隨波矢量依賴的有效磁場作用在電子自旋上, 從而使電子繞有效磁場軸進動. 而動量散射會導致波矢的隨機變化, 使有效磁場產生波動,最終導致電子系綜的自旋退相位. 因此自旋弛豫時間τs與動量散射時間τp存在這樣的一個對應關系:. 在高度簡并狀態下, 動量散射由電子-雜質散射控制, 且散射時間與溫度無關. 在本文實驗中, 光生載流子密度約為1019cm–3, 因此高度簡并狀態下的DP弛豫機制可以很好地解釋圖8b)中導帶自由電子的對溫度的弱依賴性. 當然, 在研究導帶電子自旋弛豫壽命時, 需要考慮載流子復合的影響. 因為如果載流子復合時間很短, 其復合將導致電子消失顯然也會導致自旋的消失, 也即會影響對系綜電子自旋退相位時間的測量. 但CdS晶體的自由載流子復合壽命在3 ns左右[30-31], 遠大于短壽命自旋信號的退相位時間(約為40 ps), 因此對于短壽命自旋信號而言, 載流子復合帶來的影響可以忽略. 而長壽命自旋信號的退相位時間長達4.8 ns, 大于自由電子的復合時間, 這更加證明了長壽命自旋信號是來自局域電子.

需要說明的是, 對于導帶自由電子來說, 其非均勻展寬的影響很小, 系綜電子退相位時間近似等于橫向弛豫時間(或者退相干時間)T2[32]. 室溫下導帶自由電子自旋信號的隨波長減小而減小,見圖7b). 這可能有兩方面的原因: 一方面, 波長減小, 光生載流子濃度增大; 另一方面, 波長減小也會導致電子過剩能增加. 這兩種情況都可能導致自旋弛豫時間的減小[8,14], 具體哪一種原因占主導作用,還有待于進一步研究.

3 結 論

本文采用時間分辨克爾旋轉技術, 在橫向磁場1 T條件下獲得了n-CdS單晶在不同溫度和不同泵浦探測波長條件下的電子自旋相干動力學信息:T< 60 K時, 局域電子自旋和導帶自由電子自旋均存在;T= 5 K時, 局域電子自旋退相位時間長達4.8 ns, 隨溫度升高逐漸衰減;T> 60 K時, 局域電子消失, 導帶自由電子自旋信號仍然存在并且持續到室溫, 對溫度表現出較弱的依賴性, 其自旋退相位時間約為40 ps.