改進(jìn)線(xiàn)性PID算法的直流電機(jī)控制

中國(guó)兵器工業(yè)第214研究所 姜 峰 李 亮 曹 彪

直流電機(jī)和步進(jìn)電機(jī)的運(yùn)行特點(diǎn)不同，通過(guò)設(shè)置步進(jìn)電機(jī)的運(yùn)轉(zhuǎn)步數(shù)來(lái)控制轉(zhuǎn)過(guò)的角度，而直流電機(jī)不能直接精確地實(shí)現(xiàn)旋轉(zhuǎn)角度的控制。通常會(huì)將電位計(jì)和直流電機(jī)配合使用，電位計(jì)的電位值和電機(jī)旋轉(zhuǎn)角度是一一映射關(guān)系，通過(guò)采集指示直流電機(jī)旋轉(zhuǎn)角度的電位值反饋控制直流電機(jī)旋轉(zhuǎn)的角度。處理器選擇TI的DSP的2000系列處理器TMS320F28335。

如果將DSP輸出PWM波作為輸入，將電機(jī)轉(zhuǎn)動(dòng)角速度作為響應(yīng)，那么可以認(rèn)為電機(jī)的轉(zhuǎn)速和方向受PWM波的占空比影響，如果輸出的PWM波的占空比為50%，則電機(jī)停轉(zhuǎn)；當(dāng)PWM波占空比大于50%時(shí)，電機(jī)會(huì)沿著某一個(gè)方向旋轉(zhuǎn)，此時(shí)設(shè)這個(gè)方向?yàn)檎较颍?dāng)PWM波占空比小于50%時(shí)，電機(jī)會(huì)沿著反方向旋轉(zhuǎn)，此時(shí)稱(chēng)電機(jī)反轉(zhuǎn)，而且實(shí)驗(yàn)指出占空比和電機(jī)的轉(zhuǎn)速呈現(xiàn)線(xiàn)性關(guān)系。

通常電機(jī)控制采用PID控制算法，PID控制是比例積分微分控制的縮寫(xiě)，直流電機(jī)的反饋控制算法采取改進(jìn)線(xiàn)性算法的方案，改進(jìn)算法的收斂速度優(yōu)于線(xiàn)性算法，最后會(huì)給出改進(jìn)算法和線(xiàn)性算法的對(duì)比結(jié)果。

1 線(xiàn)性算法

線(xiàn)性PID算法結(jié)構(gòu)簡(jiǎn)單靈活，實(shí)用性好，在線(xiàn)性連續(xù)控制系統(tǒng)中得到廣泛地應(yīng)用。線(xiàn)性PID算法的模型不再贅述，直接切入正題。

圖1 線(xiàn)性反饋算法和非線(xiàn)性反饋算法仿真圖

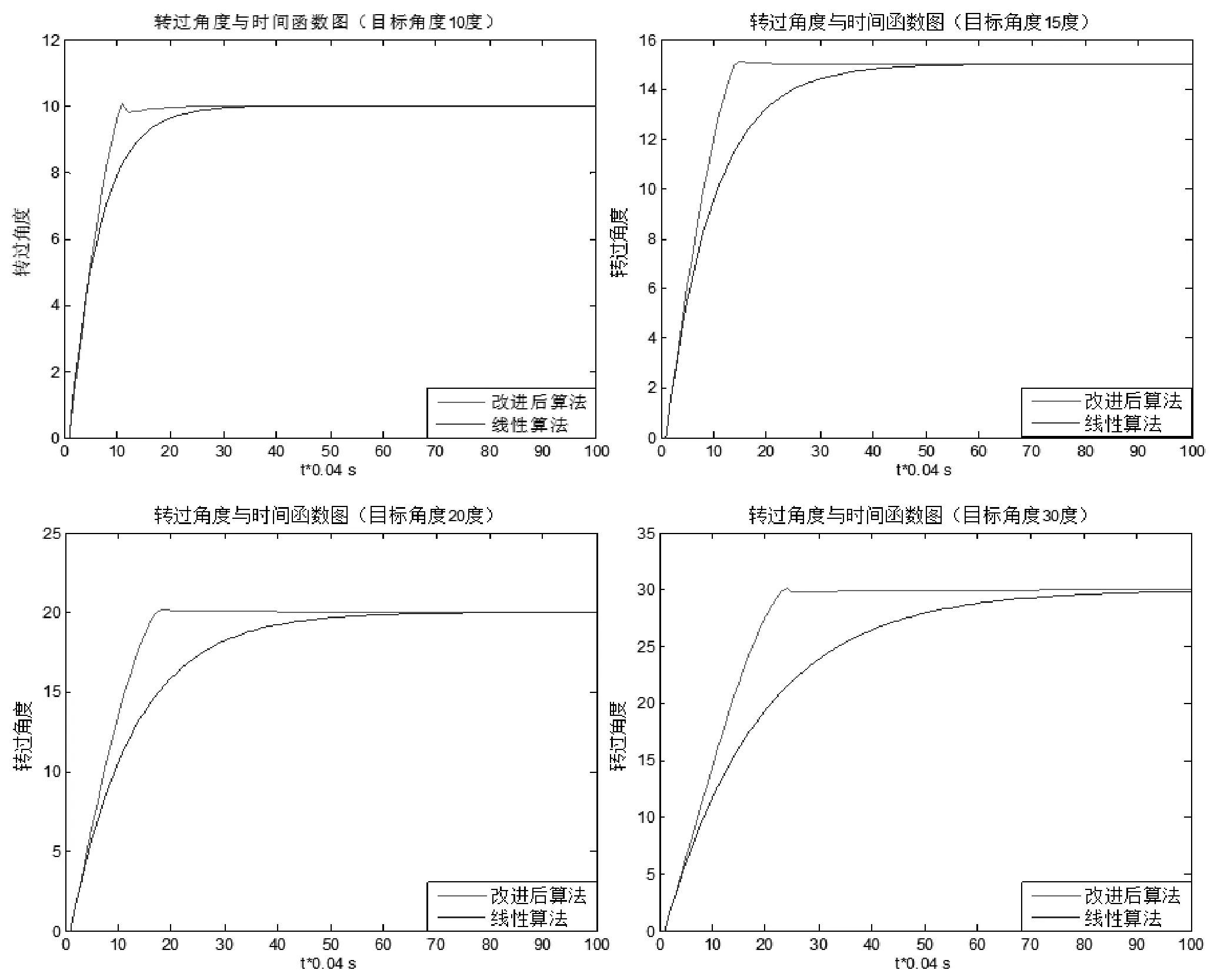
圖2 線(xiàn)性反饋算法和改進(jìn)算法仿真圖

設(shè)電機(jī)當(dāng)前的角速度為ω[n]，電機(jī)從0時(shí)刻到目前所轉(zhuǎn)過(guò)的角度為θ[n]，時(shí)間片為ΔT，即可得：

設(shè)直流電機(jī)待旋轉(zhuǎn)的目標(biāo)角度為θd，則可令：

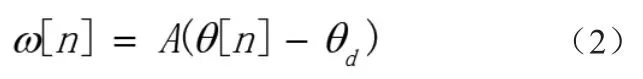
又因?yàn)檎伎毡群徒撬俣戎g呈現(xiàn)線(xiàn)性關(guān)系，且直流電機(jī)的角度位置和電位之間也呈線(xiàn)性關(guān)系，可分別記為：

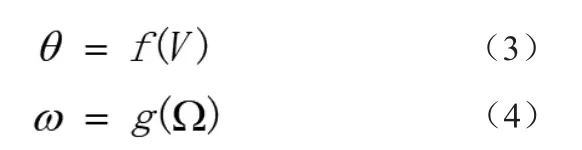
其中V為電位計(jì)指示電壓，Ω為PWM波占空比，所以上式可以寫(xiě)成：

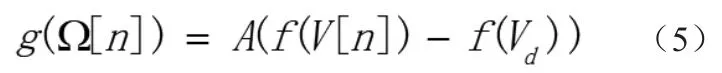
因?yàn)椋?）（3）（4）均為線(xiàn)性關(guān)系，所以（5）可以寫(xiě)成如下形式：

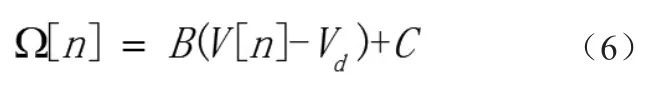
即（6）可以寫(xiě)為：

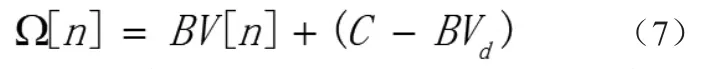
現(xiàn)已知當(dāng)某一時(shí)刻采集的電位值V[n]=Vd時(shí)，Ω[n]應(yīng)等于50%，即可得：

因?yàn)榇讼到y(tǒng)為一個(gè)因果系統(tǒng)，假設(shè)零時(shí)刻之前的沒(méi)有任何激勵(lì)，則：

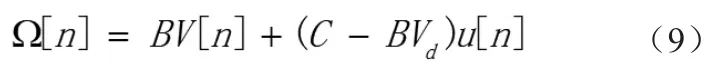
u[n]為階躍信號(hào)，則可得（9）的系統(tǒng)沖激響應(yīng)為：

δ[n]為沖激信號(hào)，（10）的Z變換為：

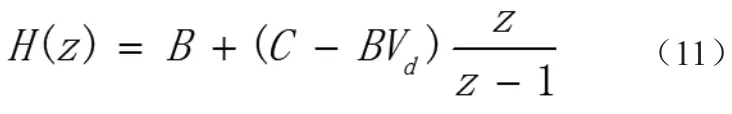
圖3 軟件流程圖

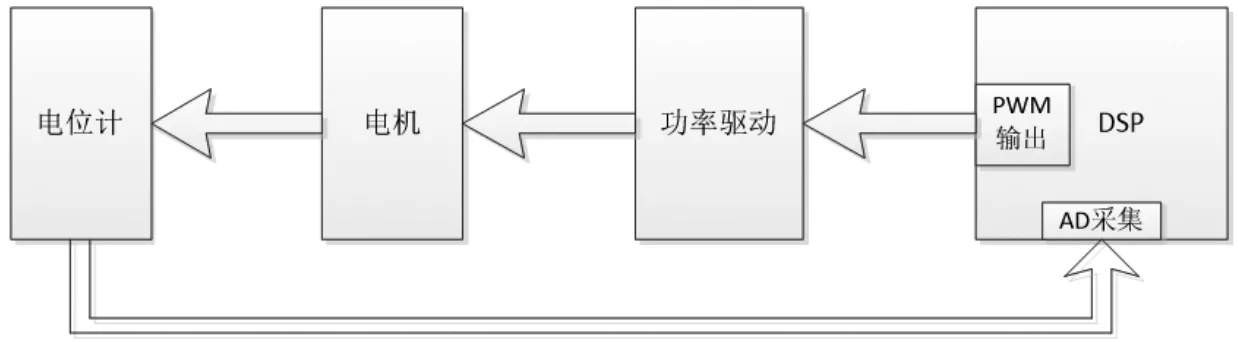
圖4 系統(tǒng)硬件連接框圖

由（12）即可得到：

由（7）和（13）可得PWM占空比和采集的反饋電位的函數(shù)關(guān)系：

2 改進(jìn)線(xiàn)性算法

由（14）可知，采集的反饋電位與指示目標(biāo)角度的電位相差越大，則DSP輸出PWM的占空比就越遠(yuǎn)離50%。若為了使系統(tǒng)盡快收斂，當(dāng)采集的反饋電位落在目標(biāo)電位附近時(shí)，PWM占空比能夠快速變化，以至于其在目標(biāo)電位處的導(dǎo)數(shù)為無(wú)窮；否則PWM波的占空比應(yīng)盡量遠(yuǎn)離50%，以使得電機(jī)能迅速轉(zhuǎn)向目標(biāo)角度，正是基于這樣的考慮，根據(jù)常數(shù)變易法的思路，構(gòu)建函數(shù)（15）：

圖1為線(xiàn)性反饋算法與非線(xiàn)性反饋算法的仿真對(duì)比圖，從仿真結(jié)果可以看出非線(xiàn)性反饋算法的收斂速度明顯優(yōu)于線(xiàn)性反饋算法，橫坐標(biāo)為時(shí)間軸，縱坐標(biāo)為電機(jī)轉(zhuǎn)過(guò)的角度，仿真設(shè)定的目標(biāo)角度分別為5°、10°、15°、25°。但是非線(xiàn)性算法并不會(huì)穩(wěn)定，而是振蕩的，這樣會(huì)導(dǎo)致電機(jī)不會(huì)停下來(lái)，而是不停地調(diào)整位置，這顯然不是想要的結(jié)果。

圖2為線(xiàn)性算法與改進(jìn)算法的仿真對(duì)比圖，從仿真結(jié)果上看，改進(jìn)后的算法繼承了非線(xiàn)性算法的收斂?jī)?yōu)勢(shì)，而且不會(huì)產(chǎn)生振蕩，可以使電機(jī)迅速轉(zhuǎn)至目標(biāo)角度。

從圖2可以看出，當(dāng)需要轉(zhuǎn)過(guò)的角度很小（小于5°）時(shí)，基于改進(jìn)的線(xiàn)性算法和線(xiàn)性算法反饋控制電機(jī)轉(zhuǎn)過(guò)該角度的時(shí)間幾乎一致；隨著待轉(zhuǎn)的目標(biāo)角度增加，改進(jìn)的線(xiàn)性算法達(dá)到目標(biāo)角度的時(shí)間明顯快于線(xiàn)性算法。

3 軟硬件實(shí)現(xiàn)

圖3為DSP實(shí)現(xiàn)直流電機(jī)控制的程序流程圖，其中V1和V2為閾值電壓，如果落在這兩個(gè)電壓之間仍舊采用線(xiàn)性算法，如果落在這兩個(gè)電壓之外，那么就采用非線(xiàn)性算法。

系統(tǒng)的硬件連接框圖如圖4所示。

總結(jié)：通過(guò)理論分析和仿真可知，改進(jìn)反饋控制算法相較于線(xiàn)性算法而言，電機(jī)轉(zhuǎn)動(dòng)到目標(biāo)位置的時(shí)間會(huì)有一定縮減，并且轉(zhuǎn)過(guò)的目標(biāo)角度越大，改進(jìn)算法的優(yōu)勢(shì)就越明顯。需要注意的是，非線(xiàn)性算法會(huì)導(dǎo)致運(yùn)算速度增加，對(duì)DSP處理器的壓力會(huì)有所增加。