某運動場地大跨樓蓋舒適度分析與控制

李學平 劉富君虞終軍

（同濟大學建筑設計研究院（集團）有限公司，上海 200092）

0 引 言

近年來，由于結構理論的發展及高強材料在建筑工程領域中的應用，大型公共建筑結構正朝著輕質、大跨、低阻尼的方向發展。尤其對于室內運動場地，由于其使用功能的需要（沒有墻體及柱分割的大空間），很容易形成低阻尼的輕質大跨樓蓋。在有節奏運動的作用下，舒適度問題成了此種樓蓋不可忽視甚至是控制性的設計問題。

用提高大跨樓蓋剛度的辦法控制其舒適度是效率低下且不經濟的；尤其是在較大有節奏運動作用下的大跨樓蓋，提高剛度的辦法效率更低。調諧質量阻尼器（tuned mass damper，TMD）對于長周期、窄頻帶的激勵作用下的結構具有很好的減振效果，為樓蓋舒適度問題的解決提供了一種很好的選擇，越來越多地在實際工程中被采用［1-3］。

本文對某大跨樓蓋進行了有節奏運動舒適度分析，并通過合理布置TMD，對有樓蓋振動進行了有效控制。

1 工程概況

1.1 項目介紹

本工程位于廊坊市大廠潮白河經濟開發區，總建筑面積約5 000 m2，建筑高度約23 m，共5層，為學校體育場館，其中一層為游泳館，三層為籃球場。結構為BRB支撐混凝土框架結構，建筑抗震設防類別為乙類，抗震設防烈度為8度（0.3g），場地類別為Ⅲ類，安全等級為二級［4］。

本項目建筑效果圖見圖1。

圖1 建筑效果圖Fig.1 Design sketch of the project

三層籃球場區采用的是鋼桁架混凝土樓板組合樓蓋，樓面承重結構采用的是兩端鉸接鋼桁架，且為滿足舒適度要求，在桁架的上弦及下弦根據計算設置了TMD。TMD主要設置在了結構豎向振動最大反應處，具體布置見圖3—圖5。結構三維模型圖見圖2。

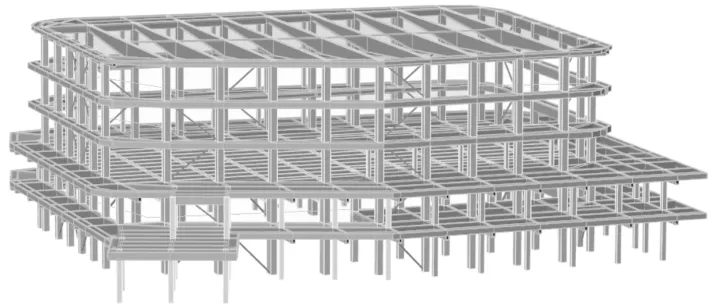
圖2 結構整體模型圖Fig.2 Structural integral model

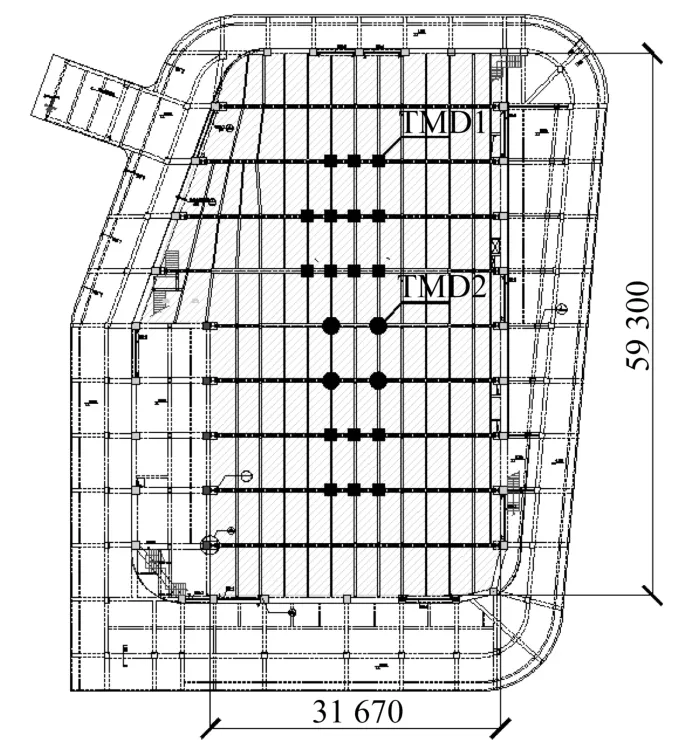
圖3 三層結構平面布置圖Fig.3 The arrangement of 3th layer

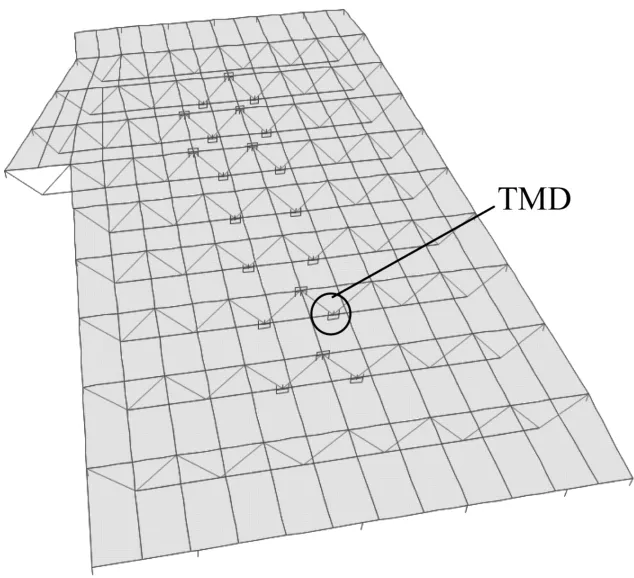
圖4 三層籃球場ETABS模型圖Fig.4 Structural model of 3th floor by ETABS

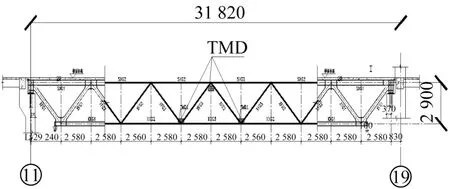
圖5 桁架立面圖（單位：mm）Fig.5 Truss elevation（Unit：mm）

1.2 結構設計概況

（1）結構先進行了合理的強度及剛度設計，桁架跨高比約1/10，桿件應力比0.8左右，各指標也均滿足規范要求。桁架概況見表1。

表1 桁架概況表Table 1 Truss overview

（2）由于鋼桁架組合樓板的部分為室內，周圍樓蓋為室外，其標高比其周圍高150 mm，周圍的約束對大跨桁架組合樓蓋部分的約束有限，故采用ETABS進行樓蓋振動分析時，只簡化取了中間桁架部分的模型。

2 舒適度分析方法及評價指標

大跨樓蓋結構在有節奏運動荷載激勵作用下產生振動，會使置身其中的人產生感官上的不適，且影響結構的正常使用，此時結構構件基本處于彈性狀態。因此，需對樓蓋結構進行振動分析，并對其舒適度指標進行評價。在樓蓋結構的舒適度分析和評價工作中，荷載激勵及評價指標的合理確定尤為重要。

2.1 樓蓋振動分析方法

由于本工程樓蓋布置對于舒適度分析而言比較復雜，故有節奏運動引起的樓蓋豎向振動加速度采用時程分析方法計算，并考慮高階模態的影響。本工程采用的分析設計軟件為ETABS，分析三維模型見圖4，桁架支座為鉸接，樓板邊界未做特別處理（因與周圍樓板有高差）。根據國家相關規范［5］，計算中，輸入取值及相關模型參數見表2。

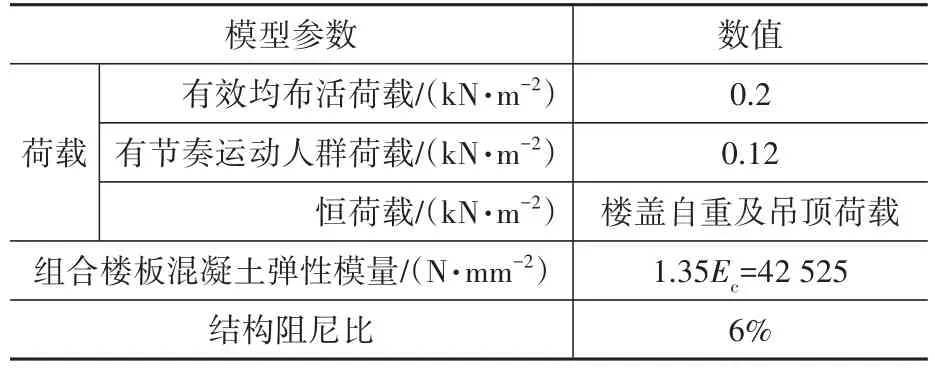
表2 模型參數表Table 2 Model parameter

2.2 荷載激勵的確定

根據國內外的研究成果，參照AISC/CISC Steel Design Guide SeriesNo.11和ATC Design Guide 1，《建筑樓蓋結構振動舒適度技術標準》（JGJ/T 441—2019）［5］給出了跳舞、有氧健身操、有氧健身操和器械健身同時進行、演唱會、體育比賽等有節奏運動的荷載函數：

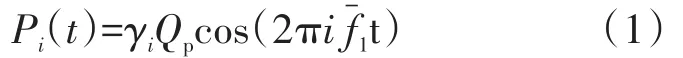
有節奏運動（室內體育活動）的第一階荷載頻率按下面公式確定：

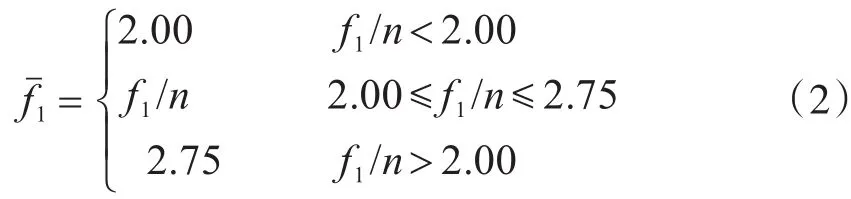
式中：f1為結構一階振型頻率（Hz）；n為取整數（1，2，3，…）。

有節奏運動的動力因子取值見表3。

表3 動力因子取值表Table 3 Dynamic factor

根據《建筑樓蓋結構振動舒適度技術標準》3.2.4條，室內運動場地的有節奏運動的人群荷載Qp取為 0.12 kN/m2。

2.3 舒適度評價標準

根據我國《高層建筑混凝土結構技術規程》［6］及《建筑樓蓋結構振動舒適度技術標準》的相關規定，樓蓋結構舒適度的控制指標包括結構自振頻率及峰值加速度兩個方面。具體評價指標見表4。

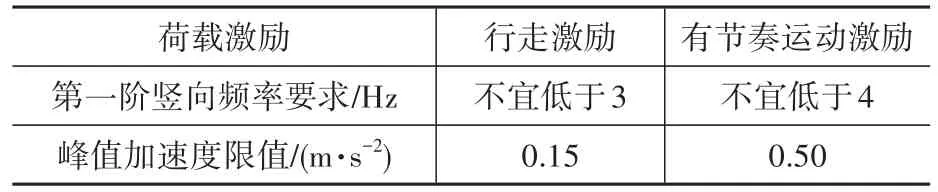
表4 舒適度評價指標要求Table 4 Comfort evaluation index

對于大跨結構，通過調整構件尺寸來實現第一階豎向自振頻率的要求很困難，且這一條不是強制性要求，故本工程在自振頻率方面設定的目標為不低于3 Hz，豎向峰值加速度的限制按規范要求取0.50 m/s2。

3 分析及減振設計結果

3.1 分析結果及評價

1）模態結果

樓蓋的前三階模態結果見圖6，由樓蓋豎向振型圖及模態質量參與分析結果可清晰地判斷出樓板振動反應的較大位置。

2）分析結果

本工程樓板豎向振動加速計算考慮結構前三階振動的反應，具體計算公式為

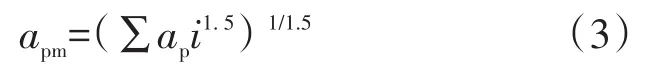
式中：apm為有效最大加速度；api為第i階荷載頻率對應的振動加速度峰值。

結構加速度反應計算結果見表5及圖6。

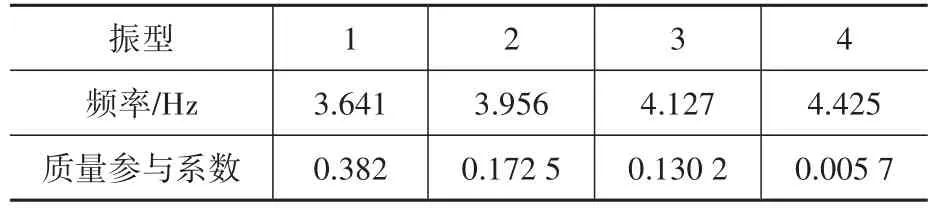
表5 結構固有振動特性Table 5 Natural vibration characteristics of structures

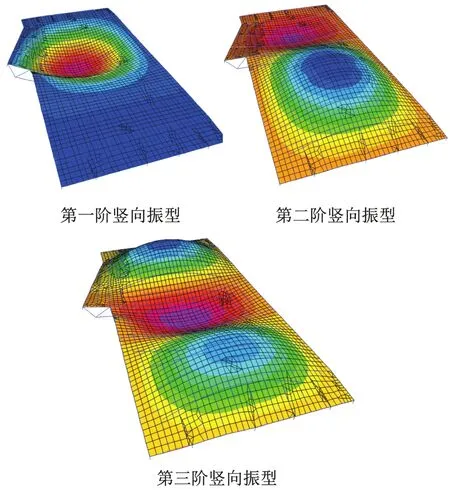
圖6 樓蓋豎向振型圖Fig.6 Vertical vibration mode diagram of the floor

由表6可知，樓板單階的最大加速度反應已顯著大于規范規定的限制（0.5 m/s2），不滿足規范要求。需要采取減振措施。

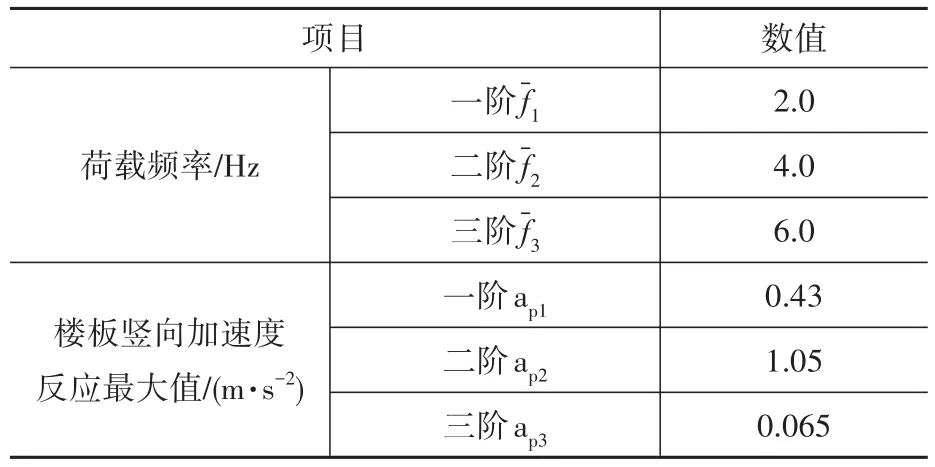
表6 結構振動特性計算結果Table 6 Calculation results of vibration characteristics

3） 減振設計

本工程采取的減振措施為在樓蓋振動較大的部位設置調諧質量阻尼器（TMD）。阻尼器的技術參數理論上需要經過比選試算得出，也可根據工程經驗直接設置。根據工程經驗，阻尼器總質量可取樓蓋前三階振動參與質量的1.0%～3.0%；本工程樓蓋較大，起控制作用的點有兩個（分別對應一階及二階振型最大反應點），且對于有節奏運動作用下的樓蓋豎向振動控制較為困難，故阻尼器總質量取較大值。阻尼器的剛度根據選取的阻尼器質量及荷載頻率根據式（4）計算得出；理論上可以根據荷載頻率設置多種頻率阻尼器，但考慮到經濟及減震效率問題，本工程只根據接近結構一階自振周期的荷載頻率設置阻尼器剛度。阻尼器的具體技術參數見表 7［7］。

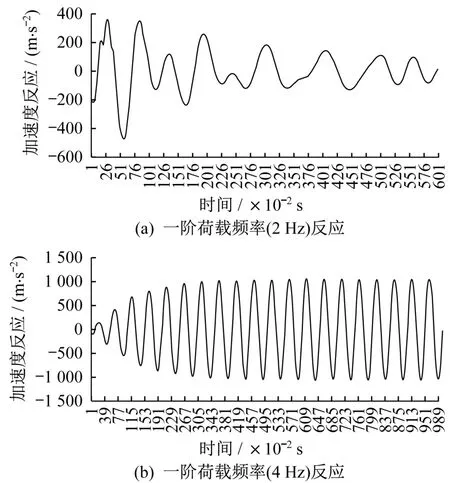
圖7 樓蓋加速度反應圖Fig.7 Floor acceleration response diagram

式中：K為阻尼器剛度；m為阻尼器質量；ω為阻尼器圓頻率。

阻尼器的位置一般放在結構主要豎向振型的最大反應點即可，經過簡單的比選試算后，本工程阻尼器具體布置圖見第一節圖3，其中方形均為TMD1，圓形均為TMD2。

設置TMD后，樓蓋對應前三階激勵的加速度反應見圖8、圖9，加速度分析結果見表8，結果選取了樓蓋一階振型最大反應點作為示例，其他點情況類似。由分析可以看出，設置TMD后，樓蓋第一和第三階荷載頻率對應的加速度反應并沒有顯著減小，但第二階荷載頻率對應的加速度反應顯著減小，減振率達60%～70%。結構的最大加速度反應出現在0.075 s，其值為0.485 m/s2，小于規范限值（0.5 m/s2）。雖然最大加速度反應較大（接近規范限值），但其發生在前面很短的時間里（0.075 s），且后面衰減得很快，所以工程上不再針對這個時間點的反應采取額外的措施。

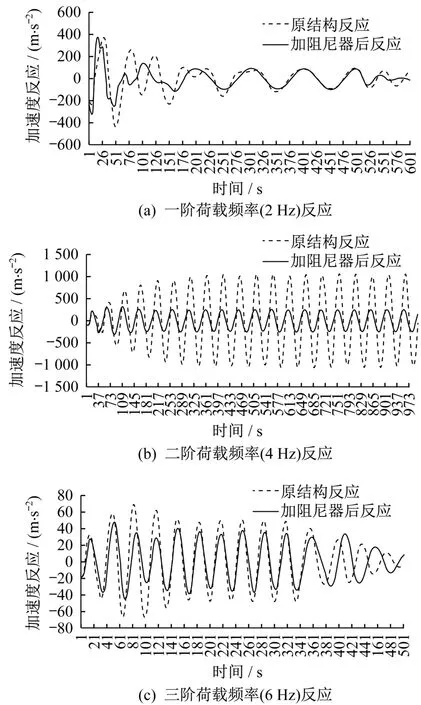
圖8 設置TMD后樓蓋加速度反應Fig.8 Acceleration response of floor with TMD

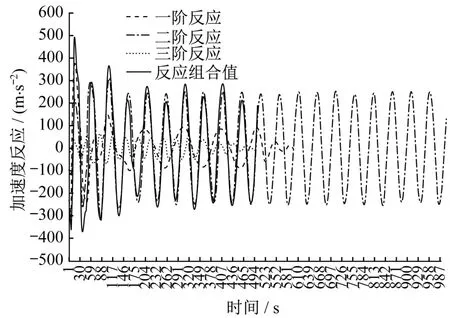
圖9 結構最大反應點組合加速度反應Fig.9 Combined acceleration response of maximum response point of structure

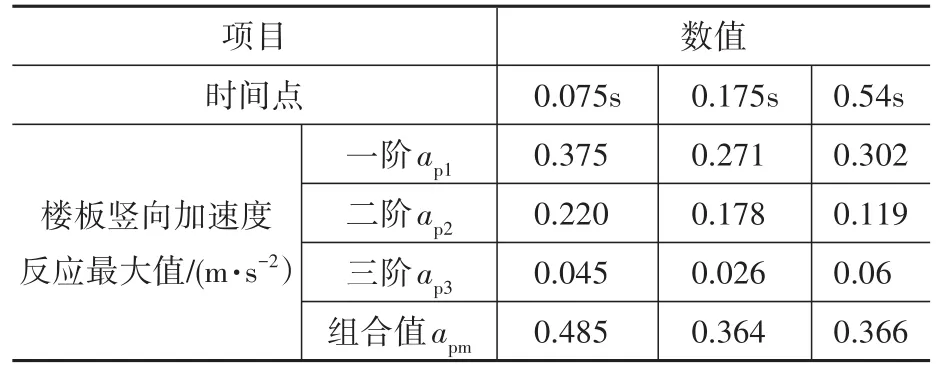
表8 樓蓋加速度反應值表Table 8 Floor acceleration response value

4 結論

本文以某大跨運動場樓蓋結構為工程實例，針對大跨樓蓋由于有節奏運動引起的振動舒適度問題進行分析，采用調諧質量阻尼器對大跨樓蓋的減振控制進行了研究，得到以下結論：

（1）有節奏運動大跨鋼結構樓蓋的設計控制條件為舒適度，在樓蓋滿足強度及剛度的條件下，還應對其進行細致的舒適度分析及設計。

（2）大跨度鋼結構樓蓋通常較難達到規范要求的頻率限值，考慮規范對此并非強制性要求，實際工程中可適當放松。

（3）調諧質量阻尼器（TMD）的減振設計可以有效地降低樓蓋在人群荷載激勵下的豎向振動，從而使樓蓋滿足舒適度使用要求。

（4）阻尼器對與阻尼器頻率接近的樓蓋頻率振動控制效果好，對其余振型振動影響很小。

（5）按照最新《建筑樓蓋結構振動舒適度技術標準》計算，設置阻尼器后，與結構自振頻率相差較遠的一階荷載頻率起了控制作用；這在以往的計算中是考慮不到的（以往計算只考慮與結構自振評率接近的荷載頻率）。