乳化瀝青冷再生混合料動態模量預估模型構建
戶桂靈, 韋金城, 韓文揚, 趙全滿, 李志剛
(1.山東建筑大學,山東 濟南 250101;2.高速公路養護技術交通行業重點實驗室(濟南),山東 濟南 250031)
0 引言
近些年冷再生瀝青混合料(Cold Recycling Asphalt Mixture,簡稱CRAM)因其壽命周期費用低、環境友好等特點得到較大規模推廣應用[1-2]。CRAM主要以乳化瀝青或者泡沫瀝青為膠結料對路面回收料RAP(Reclaimed Asphalt Pavement)進行重新利用,并添加水泥以提高其早期強度[3-4]。CRAM在大修或重建路面結構中一般用作基層,此舉也是將半剛性基層瀝青路面轉變為柔性基層路面的良好契機。模量是表征CRAM黏彈特性的重要指標,反映了混合料在荷載作用下的應力應變狀態,同時也是路面結構設計時的輸入參數,用于計算其結構層響應并預測其長期性能[5]。因此全面了解CRAM在頻率、溫度、膠結料含量等條件下的模量特性是非常有必要的。
國內外學者對CRAM的模量做了豐富研究。動態模量的大小與加載溫度、頻率、瀝青含量、水泥含量、級配和養生時間有關。室內試驗和數值模擬結果都顯示動態模量隨加載頻率降低、溫度增加而降低[1,6],添加2%的水泥可以顯著改善高溫區動態模量穩定性[3]。而在其他條件(級配、瀝青含量、水泥含量等)不變的情況下,礦粉類型對其影響并不顯著[7]。有研究表明無論是室內試件還是現場試件其動態模量均隨養生時間增加而增加,增加量為9%~14%不等[8]。較多研究中構建的動態模量主曲線顯示CRAM具有明顯的溫度和頻率依賴性,但與傳統熱拌瀝青混合料(Hot Asphalt Mixture,簡稱HMA)相比依賴性有所降低[3,9,10]。以實測溫度為輸入數據分析其力學特性,結果顯示CRAM動態模量的溫度依賴性極大影響其力學響應變化趨勢[9]。KUNA[10]等認為CRAM動態模量的頻率依賴模式與HMA的并不相同,并提出了一種新的動態模量主曲線的構建方法。
在瀝青路面結構設計中[11],動態模量作為重要輸入參數有3種水平,其中水平一需要實測材料在20 ℃、10 Hz時的模量,水平二需要通過將材料的基本參數輸入動態模量預估模型獲得,水平三則可以直接參考規范推薦值。目前雖然在研究工作中動態模量試驗進行較多,但由于動態模量試驗對測試人員的經驗要求較高、測試設備昂貴、耗時較長等原因,在這種情況下進行結構設計時,使用動態模量預估模型是較為方便的途徑。對于HMA,使用較多且效果較好的是Witzack1999模型[12]、Witzack2006模型[13]和Hirsch模型[14],這些模型基本都以材料的基本參數(集料級配、體積參數、有效瀝青含量、瀝青剪切模量等)為自變量預估動態模量[15]。對于冷再生混合料的動態模量預估模型研究較少,YAN[16]對Witzack模型進行了參數修正將其用于乳化瀝青冷再生混合料,YU[17]對含有少量瀝青瓦(Recycling Asphalt Shingles,簡稱RAS)的CRAM進行動態模量預估模型修正。
綜上所述,可以看出CRAM動態模量的研究基本上集中于其影響因素和利用動態模量評價CRAM性能方面,而在動態模量預估模型方面的研究則較少,這對不具備試驗條件和進行低水平冷再生路面結構設計時獲取動態模量較為不利。因此本文采用簡單性能試驗機,對不同類型的乳化瀝青冷再生混合料進行系列溫度頻率條件下的動態模量試驗,分析了影響動態模量的主要因素,借鑒前人建立熱拌瀝青混合料動態模量預估模型的經驗,采用逐步回歸分析法構建了乳化瀝青冷再生混合料動態模量預估模型,為不具備試驗條件或進行低水平下的瀝青路面結構設計時獲取動態模量數據提供了途徑。
1 動態模量及其預估模型
1.1 動態模量試驗和主曲線構建
動態模量試驗原理為在無側限條件下按一定溫度和加載頻率對試件施加軸向壓應力,通過測量試件可恢復的軸向應變以獲得試件動態模量[18]。瀝青混合料的黏彈性質使動態模量具有時溫依賴性。對不同溫度和頻率下測試得到的結果進行分析通常較為復雜,動態模量主曲線則提供了直觀可視的結果表達。
主曲線實質是利用線性黏彈性材料的時溫等效原理,即高溫高頻作用等同于低溫低頻作用,將不同溫度和頻率的動態模量轉換為參考溫度下的加載時間-動態模量曲線。同時由于儀器設備限制,較低溫度域的動態模量難以通過試驗得到,利用主曲線則可以對其進行估計。
AASHTO2002路面結構設計指南[19]提出利用時溫等效原理,對不同溫度下的動態模量進行水平平移至參考溫度,使用Excel規劃求解,以sigmoidal函數描述主曲線對加載頻率的依賴性。
(1)
式中:|E*|為動態模量;δ為最小模量值;tr為縮減時間;δ,α為擬合系數;β,γ為描述sigmoidal函數形狀的參數。tr為縮減時間,即參考溫度下加載時間。
(2)
logtr=log(t)-log[a(T)]
(3)
式中:t為加載時間;a(T)為時間-溫度轉換系數;T為溫度。
根據DONGRE[20]等采用瀝青剪切動態模量試驗數據得到的位移系數,同Arhennius公式既式(4),及和VTS方法確定的位移系數具有幾乎相等的數值這一結論,同時考慮參數獲取的便宜性,本文位移系數計算采用Arhennius公式,通過最小二乘法構建各混合料動態模量主曲線。
log[a(T)]=1.255 88(logηT-logηTr)
(4)
式中:ηT為當前溫度T和老化條件下的黏度(106Poise,1 Poise=0.1 Pa·s);ηTr為參考溫度Tr和旋轉薄膜烘箱(RTFO)老化條件下的黏度(106Poise,1 Poise=0.1 Pa·s)。
1.2 動態模量預估模型
力學經驗設計法將動態模量作為材料性能表征參數用來預測路面性能,而其測試方法對人員、設備和試件制作的要求均較高,實驗室條件不具備條件或者進行較低等級公路的路面結構設計時,建立動態模量預估模型是較好解決問題的途徑。目前研究人員針對熱拌瀝青混合料基于理論研究、統計回歸、人工神經網絡等方法建立了許多動態模量預估模型[12-14],其中以Witczak模型[13]和Hirsch模型[14]應用最為廣泛,模型分別見式(5)、 式(6)、 式(7)。對乳化瀝青冷再生混合料動態模量預估模型的研究較少。
0.012ρ38+
(5)
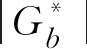
(6)
(7)
式中:E*為瀝青混合料動態模量(psi,1psi=6.97 kPa);VFA為瀝青填隙率,%;VMA為礦料間隙率,%。
2 試驗材料及方案
本文試驗選用的3種RAP回收料分別取自某高速公路A大中修項目和2條國道B、C大中修項目。回收料運送至拌合站重新破碎篩分,參考《公路瀝青路面再生技術規范》JTG F41-2019[21]級配范圍,根據篩分試驗結果,添加不同比例新集料進行級配設計,如圖1所示。選用的3種乳化瀝青按照再生規范要求進行基本性能檢測,均滿足要求,如表1所示[22]。

圖1 各試驗段乳化瀝青冷再生混合料級配設計
乳化瀝青冷再生混合料配合比設計如表2所示,A、B、C這3種RAP料分別對應A、B、C的乳化瀝青。為豐富動態模量數據,在最佳乳化瀝青含量的基礎上,針對每種RAP料,分別增加1種乳化瀝青含量,記為A1,A2,B1,B2,C1,C2,同時為研究水泥含量對動態模量的影響,對B1另增加2種水泥含量,記為B12,B13。對不同水泥含量和乳化瀝青含量的8種冷再生混合料進行動態模量試驗,試驗溫度為5 ℃、20 ℃、35 ℃、50 ℃,頻率為0.1、0.2、0.5、1、2、5、10、20、25 Hz,每種混合料進行3組平行試驗,共計獲得864組動態模量。
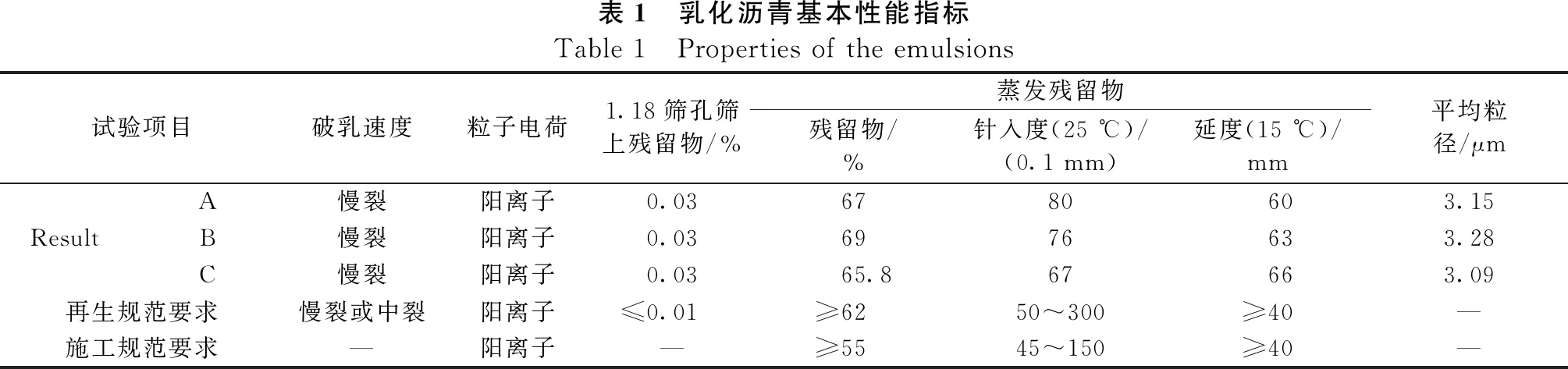
表1 乳化瀝青基本性能指標Table 1 Properties of the emulsions 試驗項目破乳速度粒子電荷1.18篩孔篩上殘留物/%蒸發殘留物殘留物/%針入度(25 ℃)/(0.1 mm)延度(15 ℃)/mm平均粒徑/μmA慢裂陽離子0.03 67 80 603.15ResultB慢裂陽離子0.03 69 76 633.28C慢裂陽離子0.03 65.867 663.09再生規范要求慢裂或中裂陽離子≤0.01 ≥62 50~300≥40—施工規范要求—陽離子—≥55 45~150≥40—

表2 乳化瀝青冷再生混合料配合比設計Table 2 Mix design for six mixtures混合料不同集料占比/%RAPNACc/%Ec/%Wc/%A183171.53.93.0A283171.53.53.4B1831733.93.0B12831723.93.0B13831713.93.0B2831723.53.4C1841623.92.6C2841624.42.1注: NA為新集料,Cc為水泥含量, Ec為乳化瀝青含量, Wc為含水量。
3 結果分析
3.1 變異分析
對各類型乳化瀝青冷再生混合料的動態模量試驗結果的變異量化分析表明:① C1和C2這2種混合料變異系數明顯較其他混合料大,可能與料源本身變異性較大有關,A1在50 ℃、25 Hz時的變異系數突然降低可能與此時的動態模量升高有關,這表明變異系數與動態模量值可能存在一定關系。② 進一步探究二者關系發現,動態模量的變異系數與動態模量平均值(3組平行試件平均值)具有良好的相關關系,變異系數隨動態模量降低而增大,動態模量降至2 000 MPa時,變異系數大約位于13%~24%之間,動態模量低于2 000 MPa之后,變異系數急劇增大,最大可達到42.1%,如圖2所示。綜合全樣本數據以冪函數形式回歸后相關關系良好,如圖3所示。
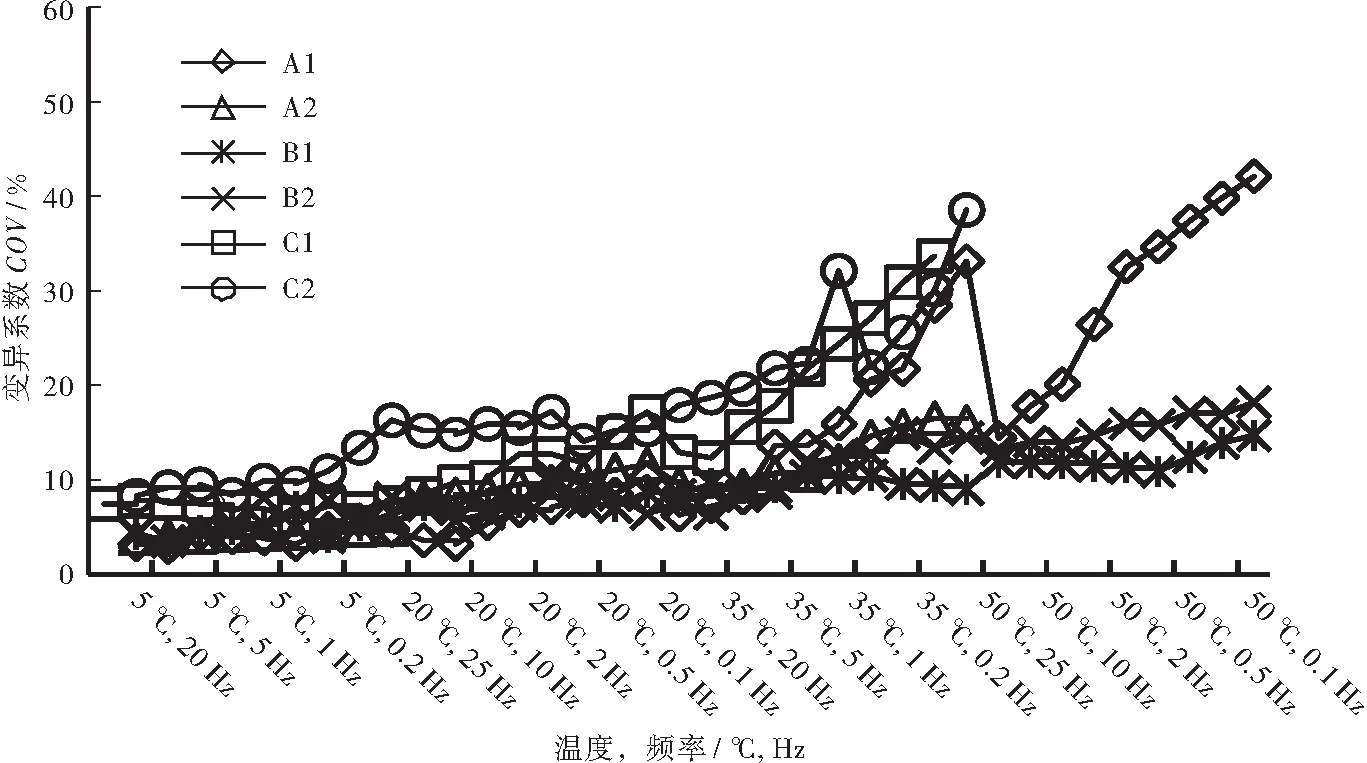
圖2 不同溫度頻率各乳化瀝青冷再生混合料變異系數
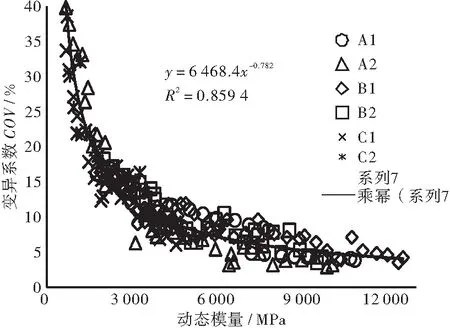
圖3 變異系數與動態模量平均值
BONAQUIST[23]等在NCHRP702報告中對熱拌瀝青混合料動態模量變異系數與動態模量值的關系進行了針對性研究,結論認為變異系數與動態模量平均值呈冪指數形式相關關系,相關程度達到0.82,并得到按照模量平均值分類的變異系數區間,將本文變異系數與其對比發現,乳化瀝青冷再生混合料動態模量的變異系數普遍大于NCHRP702報告中的值,這也間接說明乳化瀝青冷再生動態模量的變異較熱拌瀝青混合料的變異大。
3.2 水泥含量和溫度對動態模量的影響
為分析水泥含量對動態模量的影響,對國道B大中修項目中的冷再生混合料進行了3種水泥含量的動態模量試驗(見圖4),圖4結果表明:①水泥對中高溫(20 ℃,35 ℃,50 ℃)的動態模量有明顯提升作用,即提高了乳化瀝青混合料中高溫區的勁度水平。5 ℃時3種水泥含量下的動態模量差異并不明顯。②同溫度各水泥含量下頻率-動態模量曲線有集中的趨勢,說明水泥含量對動態模量的提升作用低頻時比高頻顯著。③同頻率下動態模量隨水泥含量增大。水泥含量由1%增大至2%時動態模量提升較明顯,繼續增大至3%時增大趨勢變緩,呈現出非線性形式。
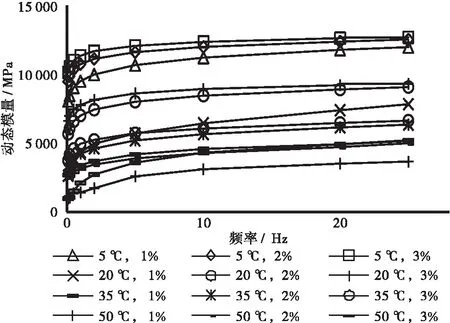
圖4 不同溫度頻率下各水泥含量的混合料動態模量值
由于老化RAP料和水泥的存在可能會使混合料在某種程度上變“硬”,因此為分析溫度和頻率對混合料的動態模量是否仍然具有顯著影響,在Origin統計軟件中采用兩因素方差分析對各類型乳化瀝青冷再生混合料進行了統計檢驗,結果如表3所示。在顯著性水平α=0.05時,動態模量各溫度頻率之間的差異統計顯著,表明溫度和頻率對乳化瀝青冷再生混合料的動態模量影響顯著,這也說明可以將乳化瀝青冷再生混合料視為黏彈性材料[3,9-10]。
3.3 動態模量主曲線
利用時溫等效原理,根據動態模量試驗結果,以20 ℃為參考溫度對不同溫度下的動態模量進行水平平移,以sigmoidal函數式(1)描述主曲線對加載頻率的依賴性,使用Excel規劃求解,建立8種乳化瀝青冷再生混合料,并與普通熱拌瀝青混合料AC[24]動態模量主曲線對比,如圖5所示。

表3 混合料動態模量溫度頻率敏感性方差分析Table 3 Two-tailed T-test statistic and corresponding P-value on dynamic modulus混合料A1A2B1B12B13B2C1C2P值溫度1.39E-231.845E-208.56E-374.58E-321.50E-242.36E-331.66E-183.06E-23頻率5.36E-113.46E-132.55E-222.63E-191.49E-143.57E-205.25E-102.60E-14
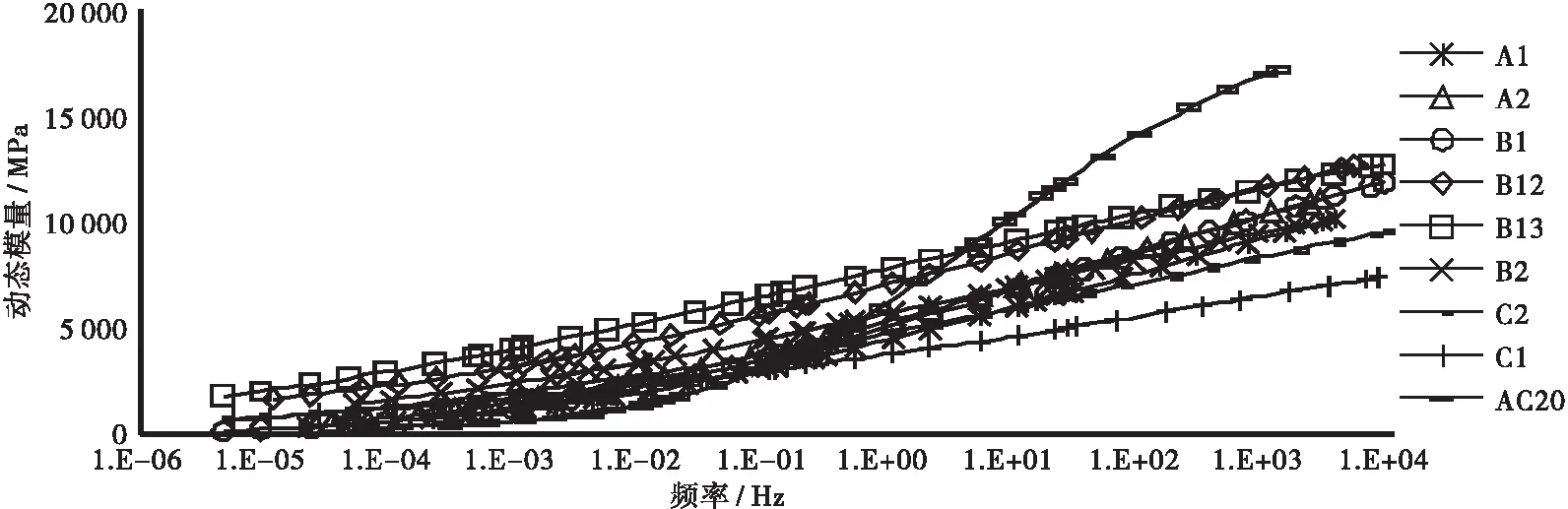
圖5 乳化瀝青冷再生混合料動態模量主曲線
由圖5可以看出:
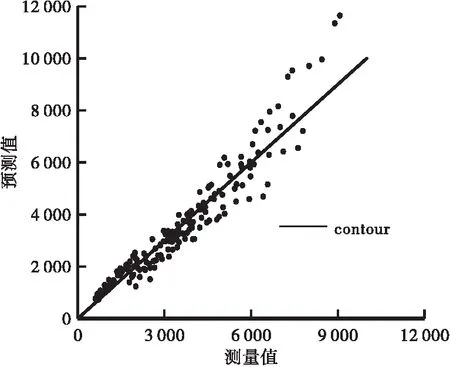
a.動態模量主曲線顯示乳化瀝青冷再生混合料隨加載頻率增大而逐漸增加,模量值均于200 MPa b.與普通熱拌瀝青混合料AC20相比,如乳化瀝青冷再生混合料主曲線發展趨勢較平順,表明其對加載頻率的敏感性有所降低。這一趨勢在中高縮減頻率區域內較明顯。 c.結合2.2節水泥對乳化瀝青冷再生混合料動態模量的影響分析,表明低頻域內乳化瀝青冷再生混合料與普通熱拌AC20動態模量隨頻率變化的趨勢大體一致,但是比較其數值可以發現前者在低頻(高溫)的勁度仍然是顯著高于后者的,水泥在相當程度上改善了高溫區乳化瀝青冷再生混合料的勁度水平。另外,水泥在高頻(低溫)區對乳化瀝青冷再生勁度的提高并不明顯。 圖6 Witzack模型動態模量|E*|實測值與預測值(單位:MPa) 圖7 Hirsch動態模量|E*|實測值與預測值(單位:MPa) 由上述預測結果與實測結果對比看出: a.各類型熱拌瀝青混合料動態模量預測模型的預測值均小于實測值,對乳化瀝青冷再生動態模量的預測均不理想,預測值偏離等值線較遠。 b.Witzack 2006模型的預測結果表明預測值與實測值兩者之間的差值先增大后減小。這可能是由于預測模型是基于熱拌瀝青混合料做出的,預測值的變化趨勢呈現出明顯的溫度依賴性。水泥的加入和乳化瀝青冷再生混合料中RAP料的老化使其溫度敏感性較前者有較大改善,中高溫區動態模量明顯增大,造成兩者之間變化趨勢并不一致。 c.在模量值較大時,預測值和實測值比較接近,這可能是水泥對低溫區(高頻)的動態模量提高不再顯著,以及RAP料本身強度較新集料有所衰減造成的。 d.Hirsch模型的預測值趨勢與Witzack基本一致。Hirsch模型以礦料間隙率VMA和基于VMA的瀝青飽和度VFA為體積特性參數,以瀝青剪切模量描述瀝青混合料的溫度依賴性。乳化瀝青冷再生瀝青混合料預測中VMA的獲得需要通過礦料合成毛體積密度Gsb,乳化瀝青冷再生混合料的級配設計中較難實現對RAP料做密度試驗,因此VMA的計算只能通過最大理論密度Gmm、瀝青含量和瀝青密度來推算。按照礦料合成毛體積密度計算方法,其值只與級配組成有關,可與瀝青含量無關。可實際推算過程中,同一級配不同瀝青含量的乳化瀝青冷再生混合料礦料合成毛體積密度并不相同。這種誤差進一步影響了VMA、VFA的計算,Hirsch模型中只有VMA、VFA和瀝青剪切模量這3個輸入參數,其中VMA與VFA輸入均存在誤差,使其對乳化瀝青冷再生混合料動態模量的預測精確度大大降低。 考慮到乳化瀝青冷再生混合料的再生特性和水泥對其溫度敏感性的影響,結合上一節現有熱拌瀝青混合料動態模量預估模型評價結果,認為對現有模型進行修正以實現乳化瀝青冷再生混合料動態模量的預估難度較大,本節利用統計學原理對各基礎因素和其組合因素進行多重線性回歸分析,構建乳化瀝青冷再生混合料動態模量預估模型。 (8) 式中:各項符號同前述公式。其中Pb為乳化瀝青中基質瀝青含量,通過蒸發殘留物百分比得到。 第3節試驗結果分析水泥對乳化瀝青冷再生混合料動態模量的影響分析顯示:水泥對抑制常溫和高溫狀態(5 ℃以上)下動態模量的衰減有顯著作用,但是對低溫(5 ℃)時的動態模量影響并不顯著。因此對乳化瀝青冷再生混合料動態模量以5 ℃為界限值,采用逐步回歸分析法[24-25]分別構建預估模型。 逐步回歸的基本思想是有進有出,具體做法是將前述變量單個引入,每引入一個自變量后,對已入選的變量逐個進行檢驗,當原引入的變量因后面變量的引入而變得不再顯著時,將其剔除。引入一個變量或從回歸方程中剔除一個變量為逐步回歸的一步,每一步都要進行F檢驗,以確保每次引入新的變量之前回歸方程中只包含顯著的變量。反復進行此過程,直到既無顯著的自變量選入回歸方程,也無不顯著的自變量從回歸方程中剔除為止,保證最后所得回歸子集是最優回歸子集。 對于高溫狀態的動態模量,統計分析軟件SPSS逐步回歸共得到7個模型,按照較小平均絕對殘差及較大復相關系數原則,最終得到5 ℃以上的乳化瀝青冷再生混合料動態模量預估模型為: 0.468 5Wc-0.471 2Va+0.064 0P0.075- (9) 調整后的R2=0.922。 式中:各符號意義同前。 對于低溫狀態(5 ℃)的動態模量,統計分析軟件SPSS逐步回歸共得到5個模型,按照較小平均絕對殘差和較大復相關系數原則,最終得到5 ℃的乳化瀝青冷再生混合料動態模量預估模型為: 0.064 5×Va-0.037 2×Vbeff+0.001 5× (10) 調整后R2=0.984。 式中:各符號意義同前。 圖8 5 ℃以上動態模量|E*|實測值與預測值(單位:MPa) 圖9 5 ℃動態模量|E*|實測值與預測值(單位:MPa) 本文通過對乳化瀝青冷再生混合料進行系列溫度頻率的動態模量試驗,分析了動態模量試驗影響因素,對現有熱拌瀝青混合料動態模量預估模型是否適用于乳化瀝青冷再生混合料進行驗證,并參考熱拌瀝青混合料動態模量預估模型參數,以5 ℃為界限分區間建立了乳化瀝青冷再生混合料動態模量預估模型,主要結論如下: a.乳化瀝青冷再生動態模量變異系數較熱拌瀝青混合料變異系數大,與動態模量平均值具有良好的相關關系,可通過冪函數式表達。變異系數隨動態模量降低而增大,動態模量降至2 000 MPa時,變異系數位于13%~24%;動態模量低于2 000 MPa之后,變異系數急劇增大,最大可達到42.1%。 b.水泥對乳化瀝青冷再生混合料中高溫區的動態模量有顯著提升作用,改善了其溫度敏感性,但對于低溫區動態模量影響不顯著。同溫度不同水泥含量時頻率-動態模量曲線有集中趨勢,說明水泥對動態模量影響低頻比高頻顯著。 c.乳化瀝青冷再生混合料動態模量主曲線表現出較明顯的時間溫度依賴性,隨溫度增大,模量降低;隨頻率增大模量增加。 d.運用熱拌瀝青混合料預估模型Witzack模型和Hirsch模型對乳化瀝青冷再生混合料進行動態模量預估,預測值和實測值之間出現由溫度敏感性差異帶來的不同。預測值表現出類似熱拌瀝青混合料的明顯受溫度和頻率影響的特點,與實測值有較大出入。這和RAP料的老化和水泥加入提高中高溫區的勁度有關。 e.基于乳化瀝青冷再生混合料動態模量隨溫度、頻率變化的特點,以及水泥、RAP料對中高溫區動態模量的提高,以5 ℃為界限分區域建立乳化瀝青冷再生混合料動態模量預估模型,結果表明新建模型可以較好地模擬實測動態模量。本模型僅基于8種類型的混合料構建,對其他乳化瀝青冷再生混合料的適用性有待進一步驗證。3.4 Witzack模型和Hircsh模型適用性驗證
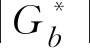

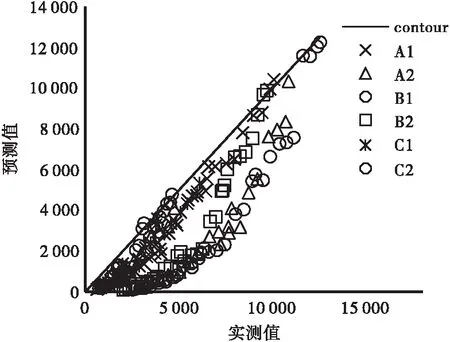
4 新動態模量預估模型構建
4.1 模型參數

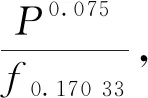
4.2 預估模型


5 結論

