LLC諧振變換器不同分析方法的比較

唐升宗

（廣東泰坦智能動力有限公司，廣東 珠海 519000）

1 4種不同的分析方法

全橋LLC諧振變換器的拓撲結構如圖1所示。

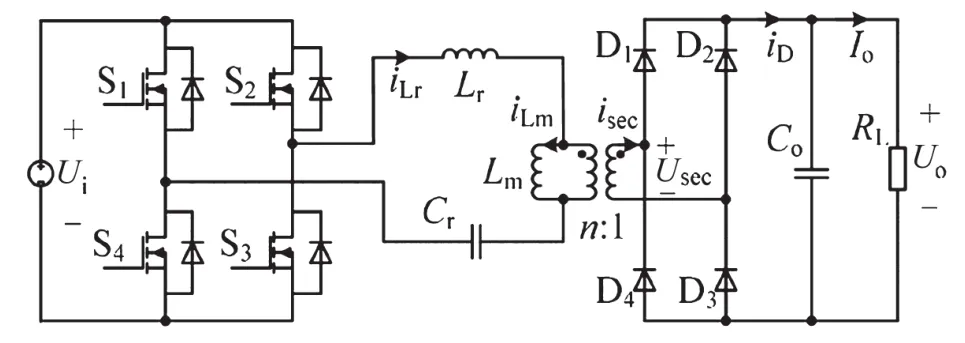
圖1 LLC諧振變換器的拓撲結構

4種分析方法的常見假設如下：一是所有開關、二極管以及無源元件都是理想的，這意味著開關和關斷過程、正向電壓和寄生參數被忽略；二是開關同一個支路的驅動信號互補，而兩支路之間的相移為180°，占空比為0.5，忽略死區時間的影響；三是在穩定狀態下，輸出電容Co上的電壓保持恒定[1]。

LLC諧振變換器在一半的開關周期內存在3個級，即當跨磁電感器Lm的電壓鉗合到正輸出電壓nUo時為P態、當跨磁電感器Lm的電壓鉗位到負輸出電壓nUo時為N級、當通過磁化電感Lm的電壓沒有被鉗住到輸出電壓時為零態[2]。根據這3個階段的順序，LLC諧振變換器主要有6種工作模式，分別為PO、PON、PN、NP、NOP以及OPO。以PO運行模式為例，在半開關周期內，LLC諧振變換器首先運行在P級，然后運行在O級。

定義電感比K、串聯諧振角頻率ωr、品質因子Q、并聯諧振角頻率ωm、歸一化開關頻率fn為：

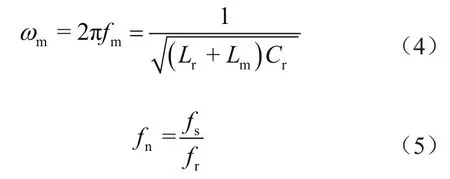
式中，Req為LLC諧振變換器的等效負載。

1.1 基波分析法

假設電力以基波的形式傳遞，變壓器二次側電流isec始終工作在臨界導通模式，在分析和建模LLC諧振變換器時只考慮電壓和電流的基次諧波[3]。

根據基波分析法，LLC諧振變換器的等效負載Req1可表示為：

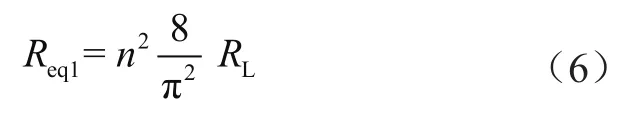
等效電路中諧振網絡輸入電壓的基次諧波Ein和變壓器一次側電壓的基次諧波E0分別為：

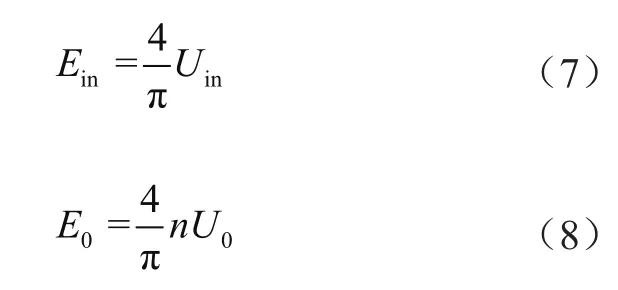
結合分壓規律可以得到LLC諧振變換器的電壓增益為：

諧振因子A1和負載因子B1的定義為：

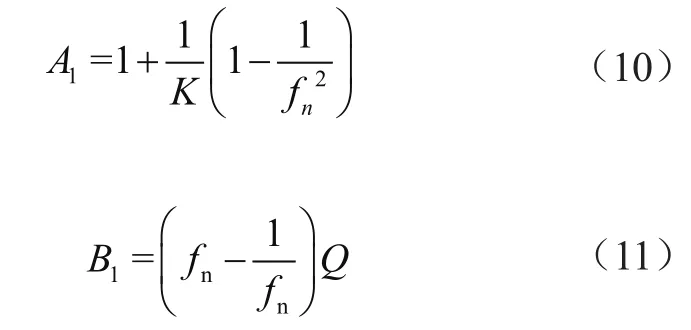
1.2 頻域與時域部分校正分析法

變壓器二次側電流isec在DCM中運行；諧振電流ILr是失真的，不能簡單的用基波諧波代替。為了提高DCM分析方法的精度，采用部分校正分析方法對負載因子進行校正[4]。

二極管的導通角為a。假設導通過程中二極管電流波形為正弦，通過對變壓器二次側電流isec進行傅里葉分析，根據能量守恒定律推導出修正后的等效負載RL為：

式中，I(1)pk為變壓器一次側電流基諧波峰值，輸出電流Io等于開關周期內二極管電流ID的平均值。

由式（12）可知，等效負載RL可表示為：

通過列出二極管導通時的電路方程，可以得到二極管導通角a的表達式。a的解析解是不可得的，為了得到a的近似解，做了一些合理假設[5]。

根據等效負載RL，利用次諧波近似（First Harmonic Approximationo，FHA）原理，該方法LLC諧振變換器的電壓增益可表示為：

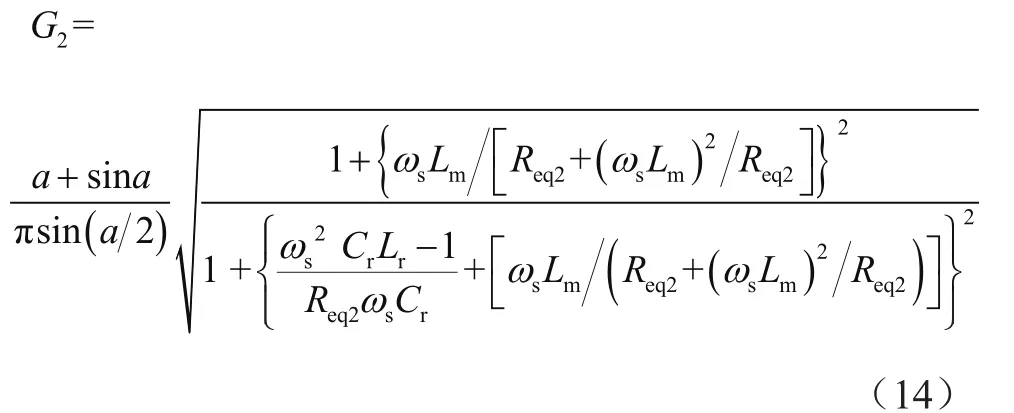
式中，ωs為角速度開關頻率[6]。

1.3 頻域與時域完全校正分析法

介紹一種結合頻域分析和時域分析的完整校正分析方法，可以同時校正諧振系數和負載系數。以PO模式為例，在不考慮負載因子的情況下，由P級電路方程可以推導出諧振電容電壓UCr(t1)與UCr(t0)的關系，然后根據O級電路方程得到UCr(t2)與UCr(t1)之間的關系[7]。在一個開關周期內，初始諧振電容電壓UCr(t0)與最終諧振電容電壓UCr(t2)對稱，即：

由式(15)，修正后的諧振因子A3可表示為：

當工作頻率接近峰值增益工作點時，LLC諧振變換器的工作模式將由PO模式變為PON或PN模式。因此，有必要對這些工作模式下的諧振因子進行進一步校正[8]。

通過對變壓器二次電壓Usec和電流isec的傅里葉分析，利用Usec和isec的基諧波可以推導出等效電阻Req3：

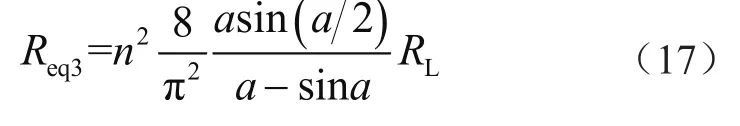
假設變壓器二次側電壓與電流之間有b/2相移，等效負載用等效電阻Req3和等效電容Ceq3表示。其中，等效電容Ceq3為：

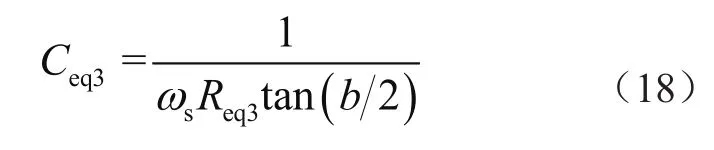
根據式（17）、式（18），可以得到修正后的品質因子Q3：

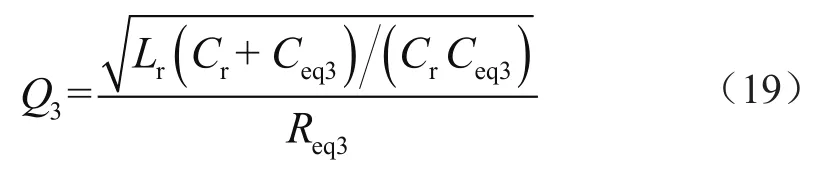
根據校正后的諧振因子和負載因子，得到LLC諧振變換器的電壓增益為：

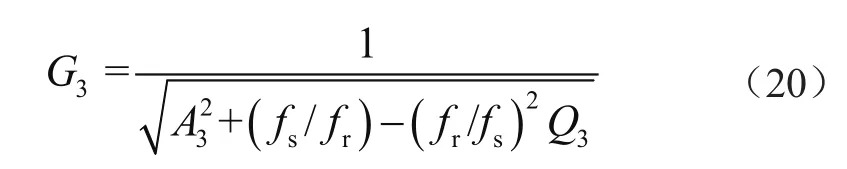
1.4 時域分析或基于操作模式的分析法

時域分析方法通過列出LLC諧振變換器在不同階段的電路方程，可以得到變換器的解析。下面以PO模式為例，按照相同的原理，也可以計算出其他的工作模式[9]。

在P態運行時，可以得到：

根據式（21）和諧振電感電流與諧振電容電壓的關系，可以得到諧振電感電流iLr和諧振電容電壓UCr的通解為：

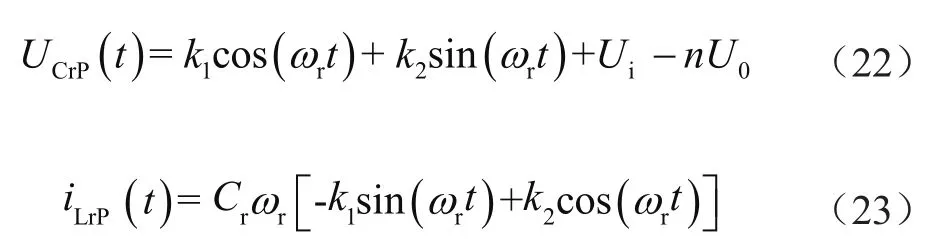
式中，k2和k2由電路的初始條件決定[10]。

在O態運行時，可以得到：

同樣，這一階段諧振電容電壓和諧振電流的一般解可以表示為：

式中，k3和k4也由電路的初始條件決定。

由式（22）、式（23）、式（25）以及式（26）可知，在PO模式下已知參數的LLC諧振變換器存在7個未知參數，即k1、k2、k3、k4、a、b以及Uo，需要7個獨立的方程來求這些值。

根據能量守恒定律，在一個開關周期內諧振網絡的輸入能量等于輸出能量；t1處P態和O態諧振電容電壓連續，諧振電感電流連續；t0處諧振電容電壓與t2處諧振電容電壓對稱，諧振電感電流對稱；t0處的磁化電感器電流與t2處的磁化電感器電流對稱；P態持續時間和O態持續時間之和等于開關周期的一半。

2 對比4種不同的分析方法

考慮到軟開關能力和變換器效率，LLC諧振變換器的工作頻率fs通常被設計為低于串聯諧振頻率fr。LLC諧振變換器的電路參數由電感比K、質量因數Q和變壓器匝數比n確定。一般情況下，變壓器匝數比n和負載RL是事先確定的，n是根據變換器輸入輸出電壓選擇的，這里選擇n=1.6進行分析。對于相同電感比K和質量因數Q的LLC諧振變換器，其對應的電壓增益曲線相同。較大的K值會降低電壓增益，擴大工作頻率范圍；而較小的K值會增加諧振電流和相應的損耗，導致效率低下。因此在實際中，K值的取值范圍為[2,10]。對于質量因數Q，大的Q值會導致諧振電容的高壓應力。此外，較大的Q值也會降低電壓增益，拓寬工作范圍。實際中，Q的取值范圍是[0,1]。

2.1 基本諧波分析

通過在頻率范圍內選擇相當多的工作點，可以繪制出不同Q值歸一化開關頻率下的電壓增益曲線，將得到的電壓增益曲線與仿真得到的電壓增益曲線進行比較。當負荷由輕負荷轉變為重負荷或Q值增大時，FHA理論結果與仿真結果的誤差增大。FHA在相鄰串聯諧振頻率工作點處的分析精度遠遠高于其他范圍，LLC諧振變換器的電壓增益隨著Q值的增加而減小。

為了評價這些分析方法的精度，將增益誤差εErrorg定義為電壓增益理論結果εCalculateg與仿真結果εRealg之間的相對誤差：

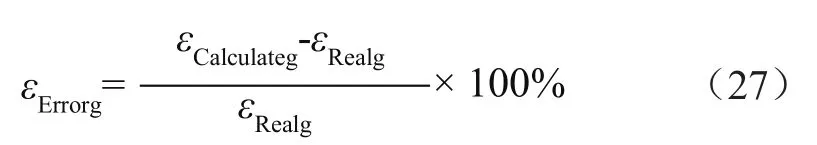
根據式（27）和工作點數據，繪制出不同Q值下的歸一化開關頻率增益誤差曲線。

2.2 頻域與時域部分校正

在相同的電路參數下，由于修正了DCM運行中的負載因子，頻域與時域部分校正法的精度得到了提高。但是，由于FHA和頻域與時域部分校正法都假設功率只能通過基次諧波傳遞，因此不同Q值的頻域與時域部分校正法的趨勢與FHA類似。同樣當誤差允許范圍設置為10%時，當Q值較小時（Q＜0.2），與FHA相比，歸一化開關頻率fn的范圍會稍寬。

2.3 頻域與時域完全校正

采用頻域與時域完全校正法對不同Q值下不同歸一化開關頻率下的電壓增益以及理論結果與仿真結果的對比。

可以得知方法2或者FHA之間的主要區別為：雖然當開關頻率遠離串聯共振頻率的時候，方法3的準確性會更糟，但是該方法在開關頻率接近時串聯共振頻率的準確性顯著提高。給出了不同Q值下方法3的增益誤差，當Q過小或過大時，誤差很大。因此，當誤差允許范圍設置為5%時，方法3的合適操作條件定義為0.2 ＜Q＜ 0.5和歸一化開關頻率fn不小于0.68。

2.4 時域分析

時域分析法的理論結果與仿真結果基本一致，增益誤差不隨Q和fn的變化而變化。然而，值得注意的是，這種方法是復雜的，需要求解非線性方程。一般情況下，LLC諧振變換器可在遠離串聯諧振頻率的情況下工作。

通過對不同Q值下4種不同分析方法的增益誤差比較，可以清楚地注意到時域分析的高精度優勢。

峰值增益頻率是LLC諧振變換器的另一個重要設計目標。峰值增益工作點出現在諧振電流與諧振輸入電壓相同時，即諧振網絡的輸入阻抗是阻性的。通常，在峰值增益頻率的右側，輸入阻抗是感性的，這是導電的一次開關的零電壓開關；在左側的峰值增益頻率，輸入阻抗是容性的，這是導電的一次開關的零電流開關。由于通常選擇金屬氧化物半導體場效應晶體管作為一次開關，其特性更適合在零電壓開關中工作，因此通過找到增益峰值頻率可以保證在電感區而不是電容區工作。然而，由于分析方法的準確性不同，理論峰值增益頻率與實際峰值增益頻率之間存在誤差。

為了評價不同分析方法對峰值增益頻率的準確性，將峰值增益頻率誤差定義為理論值與真實值的相對誤差，即：

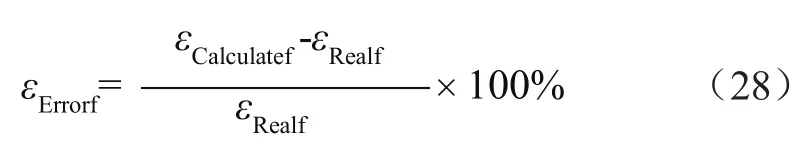
不同Q值下不同分析方法的峰值增益頻率誤差：（1）當Q較小時，方法1和方法2的峰值增益頻率誤差相對較小；（2）當Q較大時，方法3的峰值增益頻率誤差較小；（3）在整個范圍內，方法4的峰值增益頻率與仿真結果完全相同。

結論：（1）當Q=0.1時，方法1和方法2無論是在電壓增益誤差還是在峰值增益頻率誤差方面都優于方法3；（2）當0.2

4種分析方法的特點如下：（1）FHA：FHA的推導簡單，但準確性是4種方法中最低的；（2）頻域帶時域偏校正：該方法推導相對簡單，精度較FHA方法略有提高；（3）頻域時域完全校正：該方法在方法2的基礎上進行進一步校正。這種方法的推導是復雜的。雖然Q過小或過大時精度較差，但在串聯諧振頻率附近的精度有了顯著提高；（4）時域分析：該方法在推導過程中不做任何額外的假設。在整個工作范圍內保證高精度。它的主要缺點是推導和求解都很復雜。

3 實驗結果

從以上分析可以看出，除域分析外，其他3種方法在工作點遠離串聯諧振頻率點時誤差均較大，主要原因是在這個工作范圍內諧振電流或二極管電流的波形不能簡單地看成是正弦，而要用它們對應的基諧波來代替。從時域分析的角度來看，當LLC諧振變換器的開關頻率從串聯諧振頻率變為較低值時，變換器的工作模式可能會由OPO模式變為PO模式，再變為PON模式。此外，當負載由輕負荷轉變為重負荷或質量因數Q由低值轉變為高值時，LLC諧振變換器的工作模式也會由OPO模式轉變為PO模式，再轉變為PON模式。

當Q=0.2時，得到了不同開關頻率下的實驗結果。變換器的工作模式為PON模式。諧振電感電流和變壓器二次側電流均發生畸變，不能簡單地看成是正弦。這也是為什么當開關頻率遠離串聯諧振頻率時，方法1、2、3有較大誤差的原因。

該變換器工作在PO模式下，諧振電感電流和二極管電流波形接近正弦。因此，方法1、2、3的誤差較小。

顯然，轉換器工作在OPO模式下，諧振電感電流幾乎是正弦的。因此，該區域分析方法的準確性進一步提高。

當負載較大或質量因數Q較大時，LLC諧振變換器工作在PON區域，諧振電流iLr不能簡單地看成是正弦。另一方面，當負載較輕或Q較小時，諧振電流iLr更加正弦化，因此在Q較小時，前3種分析方法具有較高的精度。實驗結果與理論分析結果一致。

實驗結果與時域分析結果基本一致。另外，當工作頻率接近串聯諧振頻率時，由于諧振電感電流的高質量正弦波形，其他3種分析方法的誤差相對較小。相反，當開關頻率遠離串聯諧振頻率時，誤差更大。實驗結果與理論分析結果一致。

4 結 論

本文介紹了LLC諧振變換器的4種分析方法。然后結合具體情況，對4種方法的精度進行綜合比較。分析結果表明，當品質因子Q較小時，工作頻率接近串聯諧振頻率時，FHA具有較高的精度。頻域經時間域部分修正的方法與FHA具有相似的特性，精度略有提高。時域完全校正的頻域方法當Q在適當范圍內具有較高的精度，與前兩種方法相比，接近串聯諧振頻域的精度有所提高。時域分析在整個工作范圍內都能保證較高的精度，且其精度不隨品質因子Q和電感比k的變化而變化。最后搭建了實驗樣機，驗證了理論分析的正確性。

本文的主要研究重點和貢獻是介紹了LLC諧振變換器的4種分析方法的原理。另外，基于電壓增益誤差和峰值增益頻率誤差對不同分析方法進行了綜合比較。最后，總結了不同分析方法的適用范圍，為工程師分析和設計LLC諧振變換器提供指導。