基于ROS室內巡檢機器人的視覺慣性融合定位方法

孫希君 王秋瀅 王水根 吳應為

摘 ?要：精確魯棒的定位系統是保證室內巡檢機器人正常工作的重要基礎。文章基于機器人操作系統（ROS），針對現有公開視覺算法ORB-SLAM2在低性能計算平臺上因計算能力不足導致的特征跟蹤丟失問題，提出一種將ORB-SLAM2與慣性導航系統（Inertial Navigation System， INS）解算誤差進行卡爾曼濾波融合的方法。經公開數據集驗證表明，該方法能夠完整地估計出視覺失效時丟失的位姿信息，與ORB-SLAM2相比，定位系統的精度與魯棒性有效提高。

關鍵詞：ROS;定位;卡爾曼濾波;ORB-SLAM2

中圖分類號：TP242 ? ?文獻標識碼：A文章編號：2096-4706（2021）13-0139-06

Visual Inertial Fusion Positioning Method Based on ROS Indoor Inspection Robot

SUN Xijun1， WANG Qiuying2，3， WANG Shuigen4， WU Yingwei1

（1.College of Information and Communication Engineering， Harbin Engineering University， Harbin ?150001， China; 2.College of Underwater Acoustic Engineering， Harbin Engineering University， Harbin ?150001， China; 3.Key Laboratory of Underwater Acoustic Technology， Harbin Engineering University， Harbin ?150001， China; 4.Yantai Iray Technology Co.， Ltd.， Yantai ?264006， China）

Abstract： Accurate and robust positioning system is an important basis to ensure the normal operation of indoor inspection robot. Based on the robot operating system （ROS）， aiming at the loss of feature tracking caused by the insufficient computing power of the existing public vision algorithm ORB-SLAM2 on the low-performance computing platform， this paper proposes a method for Kalman filter fusion in the solution errors of ORB-SLAM2 and inertial navigation system （INS）. The verification of public data sets shows that this method can completely estimate the pose information lost when visual failure. Compared with ORB-SLAM2， the accuracy and robustness of the positioning system are effectively improved.

Keywords： ROS; positioning; Kalman filter; ORB-SLAM2

0 ?引 ?言

在化學工業工廠、電力設備廠房、電力隧道、物流倉儲庫房等室內高危作業環境下，配備24小時持續巡檢機器人可有效提升作業人員的工作效率，并在極大程度上保證員工安全問題。確保巡檢機器人正常工作的關鍵前提是機器人自身可以實現高精度、高可靠性的實時自主定位。

常見的用于單一定位系統的傳感器主要有衛星接收機、激光雷達、視覺相機、慣性測量單元（Inertial Measurement Unit， IMU）由于建筑物遮擋等影響室內機器人無法通過衛星信號進行精準定位，激光雷達的價格相對昂貴，而視覺相機與IMU的成本相對低廉、且無須外界提供任何信息便可進行獨立自主定位，因此利用視覺相機與IMU進行運載體的定位逐漸引起學術研究者的廣泛關注[1]。

現有的純視覺算法都存在著易受光照、相機快速運動等問題的影響，基于直接法的DSO（Direct Sparse Odometry）算法[2]在計算速度上相對較快，但是對光照尤其敏感，在實際場景中很難保持穩定的曝光時間以至于系統經常無法正常工作;基于特征點法的Orb-slam算法[3]在相機平穩運動時定位精度較高，但在相機快移動或光照突然變化等復雜動態場景下會出現跟蹤丟失[4]無法檢測特征點的問題。本文基于ROS（Robot Operating System）開發平臺，驗證分析了ORB-SLAM2算法的實際效果，并針對算法出現的問題提出一種與IMU誤差狀態進行卡爾曼濾波融合的方法來對視覺信息進行補償修正，解決了復雜場景下純視覺算法跟蹤丟失的問題，提高了系統的定位精度與魯棒性。

1 ?ORB-SLAM2視覺算法

ORB-SLAM2算法是目前非常完善的主流視覺SLAM算法之一，它通過提取并匹配圖像中的ORB特征來逐幀估計相機的位置與姿態。整個算法由三個線程分別進行，跟蹤線程負責ORB特征的提取與相機位姿估計并確定是否需要引入關鍵幀，局部建圖線程負責處理新的關鍵幀并完成局部地圖的創建，采用局部束調整的方法來篩選去除多余的關鍵幀，對局部空間內的特征點與相機位姿進行求解，閉環檢測部分則對全局的地圖與關鍵幀進行檢測與校正以消除累積誤差。其最大的優點是在于它在原有的視覺里程計基礎上增加了閉環檢測線程，保證了相機軌跡與地圖的全局一致性，一定程度上避免了累積誤差對系統帶來的影響。ORB-SLAM2算法的整體流程圖如圖1所示。

但ORB-SLAM2算法采用的三線程結構也對計算機的CPU負荷能力有更高的要求，當相機快速運動引起圖像模糊或者光照強度突變時，在性能較低的計算機或嵌入式系統上將無法正常工作，會出現特征點跟蹤丟失的問題。因此，本文在原有的ORB-SLAM2算法基礎上做了改進，將其與慣性導航誤差狀態做卡爾曼濾波融合，用慣性導航解算的誤差修正ORB-SLAM2算法在特征跟蹤丟失時的位姿誤差，并將誤差反饋到子系統中進行迭代修正，使其可以在低性能計算平臺上更穩定地自主工作。

2 ?濾波融合定位算法

多傳感器融合主要包括緊耦合和松耦合2種基本框架。松耦合是指各子系統分別解算后再融合，緊耦合則是在系統前端將各子系統的測量參數均加入模型中，狀態量維度的提高使得緊耦合算法的計算量也更大，為不再額外增加平臺的計算負擔且便于后續研究中視覺算法的輕量化改進，本文采用松耦合框架來構建模型實現視覺慣性的數據融合。

2.1 ?構建IMU誤差狀態模型

本文利用IMU自身的傳感器誤差及解算得到的導航信息的誤差作為狀態量進行建模，微小量誤差相對于直接將導航信息作為狀態量的方法在線性化過程[5]中得到的結果更為精確。

IMU測量獲取到的原始數據的計算公式為：

ai=Riw（i）（aw-gw）+ab+an ? ? ? ? ? ? ? ? ? ? ?   ? ?（1）

ωi=ωw+ωb+ωn ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （2）

其中，ai、aw、ab、an分別表示加速度計在傳感器坐標系下測得的帶誤差的實際加速度、世界坐標系下不帶噪聲的真實加速度、加速度計自身零偏、測量過程中加速度計產生的隨機噪聲，gw表示重力向量，Riw（i）表示在慣性導航模塊中定義的世界坐標系到IMU坐標系的旋轉矩陣，本文中直接將IMU坐標系作為世界坐標系，ωi、ωw、ωb、ωn分別表示陀螺儀在傳感器坐標系下測得的帶誤差的實際角速度、世界坐標系下不帶誤差的真實角速度、陀螺儀自身零偏以及測量過程中陀螺儀產生的隨機噪聲。

慣性導航解算中對加速度進行一次積分獲取速度信息，再進行二次積分獲取位置信息，本文為避免歐拉角萬向鎖的影響，采用漢密爾頓表示法的四元數來描述姿態信息[6]。實際場景中自主運動機器人的運動學模型會受隨機誤差及IMU內部噪聲的影響，本文假設兩種噪聲均為高斯白噪聲。結合上述IMU測量的計算公式可推導出真實狀態下的運動學微分方程為：

Pw（i）=vw（i）

vw（i）=aw=Riw（i）T（ai-ab-an）+gw

qw（i）=qw（i）ωw=qw（i）（ωi-ωb-ωn）

ab=aε

ωb=ωε ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（3）

其中pw（i）、vw（i）、aw、ωw分別表示機器人在世界坐標系下的位置、速度、加速度與角速度信息，qw（i）表示機器人在三維空間中的方向信息，ab、ωb分別表示慣性測量單元加速度計與陀螺儀的零偏誤差，aε、ωε分別表示加速度計與陀螺儀的隨機游走噪聲，該世界坐標系在本文中即為IMU坐標系。

理想狀態下的運動學模型是在假設不存在外界隨機誤差及傳感器內部偏差的情況下建立的，忽略掉噪聲影響，理想的標稱運動學微分方程為：

Ps=vs

vs=as=Riw（i）T（ai-ab）+gs

qs=qsωs=qs（ωi-ωb）

abs=0

ωbs=0 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （4）

其中ps、vs、qs分別表示機器人在世界坐標系下的理想位置、速度、四元數姿態信息，as、ωs分別表示不考慮零偏誤差的加速度、角速度信息，gs表示理想重力加速度，abs、ωbs分別表示理想情況下的加速度計與陀螺儀零偏誤差。

將真實狀態運動學方程與理想狀態運動學方程聯立作差，便可推算出IMU解算信息誤差以及傳感器內部隨機游走誤差的運動學模型：

δp=δv

δv=-Riw（i）T[ai-ab]×δθ-Riw（i）Tδab+δg-Riw（i）Tan

δθ=-[ωi-ωb]×δθ-δωb-ωn

δab=aε

δωb=ωε ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（5）

其中，δp=pw（i）-ps表示位置誤差，δv=vw（i）-vs表示速度誤差，δθ表示旋轉的角度矢量，由qw（i）=qseδθ/2計算得到，δab=ab-abs表示加速度計誤差，δωb=ωb-ωbs表示陀螺儀誤差，δg=gw-gs表示重力加速度誤差，本文將其忽略不計，即取δg=0，[·]×表示反對稱矩陣。

2.2 ?創建觀測模型

ORB-SLAM2利用采集到的圖像數據可逐幀估計出相機的位姿信息，在ORB-SLAM2中位姿信息由跟蹤線程中的函數返回，在此基礎上，本文用4×4的剛體變換矩陣Tcw（c）來描述ORB-SLAM2算法返回的相機姿態，其公式為：

（6）

其中3×3矩陣Rcw（c）表示相機在世界坐標系中（相機的初始幀坐標系記為相機當前對應的世界坐標系）由初始幀到當前幀姿態的旋轉矩陣，三維向量tcw（c）是用來描述相機在該世界坐標系下的位置的平移向量，該矩陣描述的是相機坐標系到世界坐標系的變換關系。對該矩陣求逆即可得到相機的外參矩陣，由于旋轉矩陣為正交陣，故可推導出轉換公式為：

（7）

由旋轉矩陣和平移向量可以推導出相機的三維位置和姿態四元數信息，位置計算公式為：

pcx=tcw（c）（1，1）

pcy=tcw（c）（2，1） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（8）

pcz=tcw（c）（3，1）

其中pc=[pcx，pcy，pcz]T表示相機測量到的相機坐標系下的位置信息。

測量誤差為觀測值與理想預測值的殘差，本文中預測值通過IMU解算得出，因此需要將相機坐標系下的位姿信息轉換到IMU坐標系下進行空間同步，相機坐標系到IMU坐標系的轉換關系可通過標定得出，記旋轉關系為Ric，平移關系為pic，可推導出相機在IMU坐標系下的位置：

（9）

其中pi=[pix，piy，piz]T表示相機測量到的在IMU坐標系下的位置信息，三個坐標系的空間變換過程為：

Riw（c）=RicRcw（c） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （10）

其中Riw（c）表示相機從相機的世界坐標系到IMU坐標系的旋轉矩陣，有qi=[qiw，qix，qiy，qiz]T，qiw為實部，則相機由世界坐標系到IMU坐標系下的姿態四元數信息轉換公式為：

（11）

由上述兩組公式可以構建出3維位置觀測誤差模型：

δpi=pi-ps ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（12）

通過以下公式可以推導出4維旋轉矢量角模型：

（13）

2.3 ?濾波融合定位算法

在數據融合過程中將所有需要估計的信息列入狀態量中，可用來進行輔助修正的信息列為觀測量，本文中將IMU的解算誤差及傳感器內部隨機游走誤差作為狀態量，記X=[δp ?δv δθ ?δab ?δωb]T，觀測量為已與IMU進行空間同步的視覺模塊觀測到的位姿誤差，記Z=[δpi ?δθi]T。融合定位算法的總體流程如圖2所示。

以慣導系統的預測誤差作為狀態量，視覺解算的誤差作為觀測量，進行卡爾曼濾波融合過程，當ORB-SLAM2算法可以正常工作時相信觀測模型，在視覺特征跟蹤丟失時相信預測模型，為使IMU的預測精度更高，在每一次迭代后將更新得到的估計誤差控制量反饋到慣導系統內部對狀態量進行校正，記更新后的估計誤差為δx=[δp ? ?δv ? ? δθ ? ? δab ? ? ? ?δωb] T，通過以下公式可計算得到經過校正的信息：

（14）

其中p為定位系統估計的新位置信息，q為新姿態四元數信息。

3 ?驗證及分析

該融合算法完全基于kinetic版本的ROS開發測試，實驗環境為Ubuntu16.04系統，CPU為英特爾i5-8300H。為驗證分析本文融合定位算法的有效性，本文采用蘇黎世聯邦理工學院ETH公開的室內視覺慣性數據集對ORB-SLAM2算法和改進后的融合算法性能進行對比測試。該數據集的信息由搭載了雙目VIO相機和運動捕捉系統的微型飛行器來采集，數據集中包含雙目圖像、已進行時間同步的IMU測量值以及精確的地面真值，其傳感器的裝配坐標系如圖3所示。

由于IMU安裝在飛行器的正中心，IMU坐標系與飛行器的本體坐標系重合，因此，本文將視覺估計信息轉換到IMU坐標系下進行解算得到的位姿即機器人的實際位姿。

對ORB-SLAM2算法進行驗證，在飛行器運動過程中，相機在正常工作狀態下ORB特征點跟蹤情況如圖4所示，當相機受到光照變化等環境因素影響時，跟蹤線程無法正常工作，如圖5所示部分出現特征點跟蹤丟失的問題。

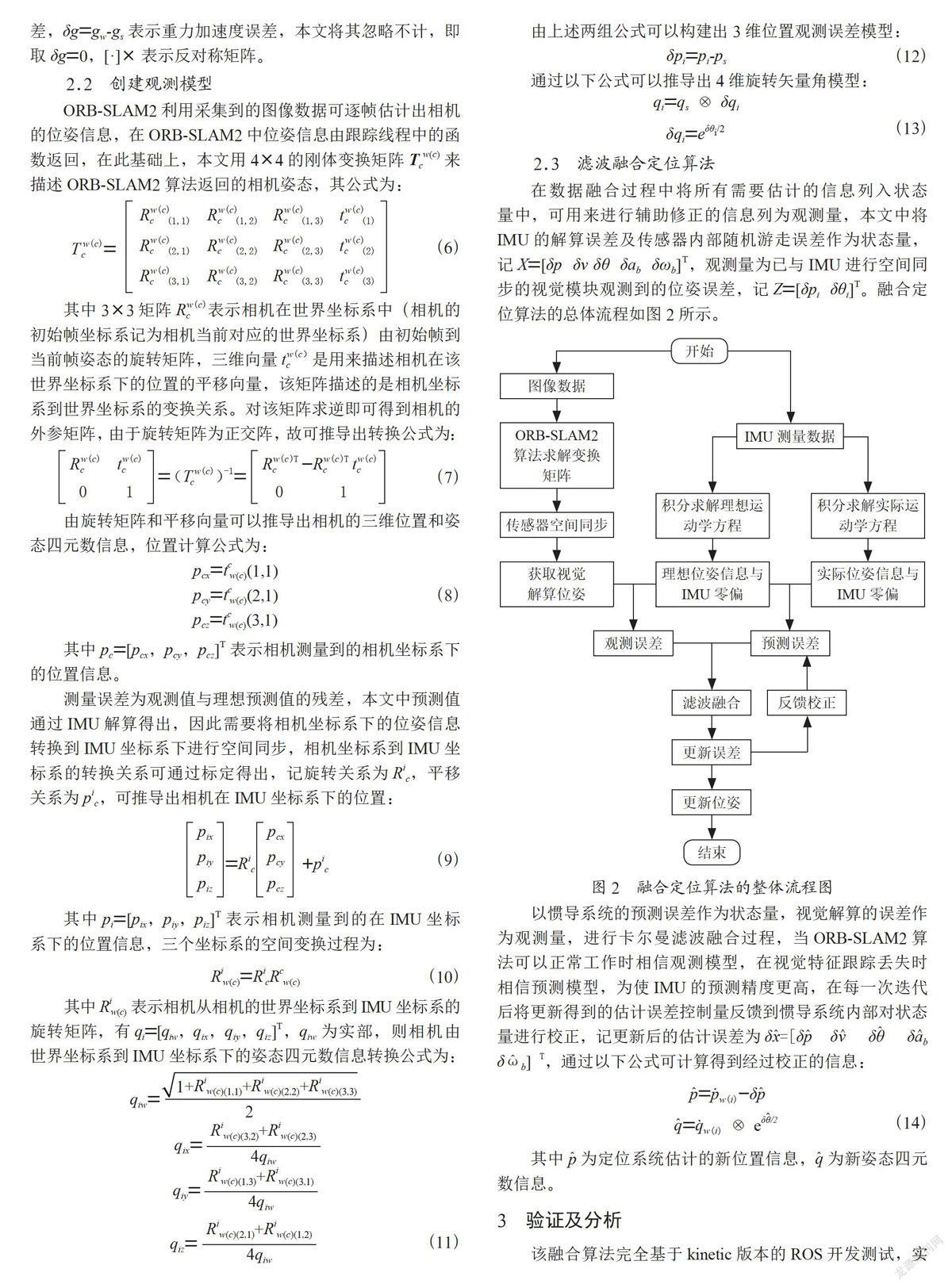
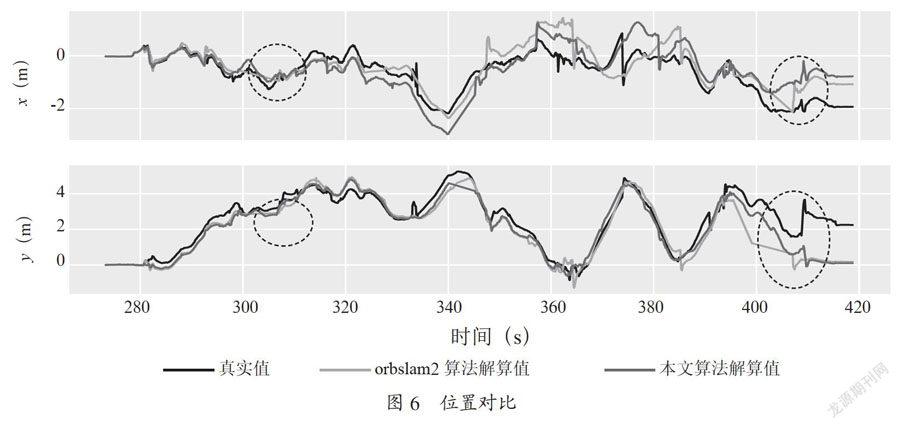
ORB-SLAM2算法的三線程使其對運行平臺的計算能力要求較高，因此就出現了上述跟蹤丟失的狀況。將其解算得到的位姿信息、本文的融合位姿信息與運動捕捉系統采集到的基準值作對比，二維位置信息對比如圖6所示，橫滾、俯仰、偏航三個方向的姿態角信息對比如圖7所示。

由圖6與圖7可以看出視覺算法定位過程中出現兩次特征跟蹤丟失的狀況，ORB-SLAM2在本實驗平臺上的魯棒性較弱，當CPU負擔較大時，跟蹤線程無法正常工作，就會出現如圖中的丟失狀況，定位精度大大降低。而本文的算法解決了視覺跟蹤丟失的問題，在跟蹤丟失時以IMU的估計值去校正結果，經過校正的估值更趨近于基準值。

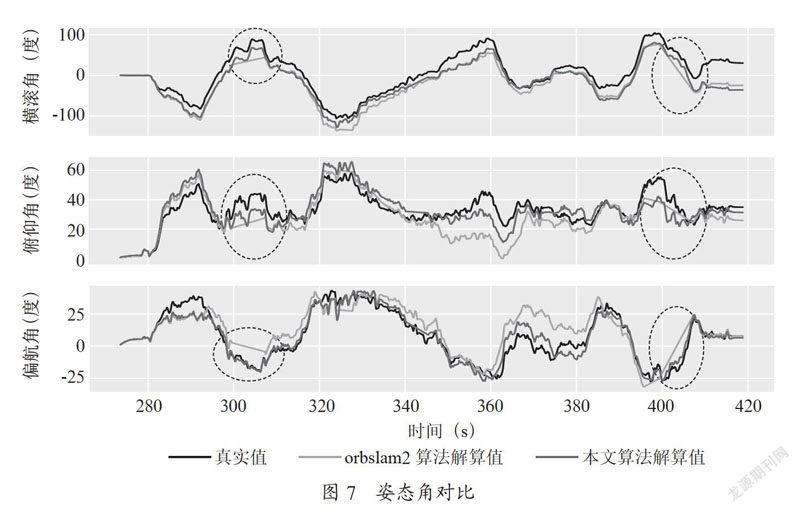
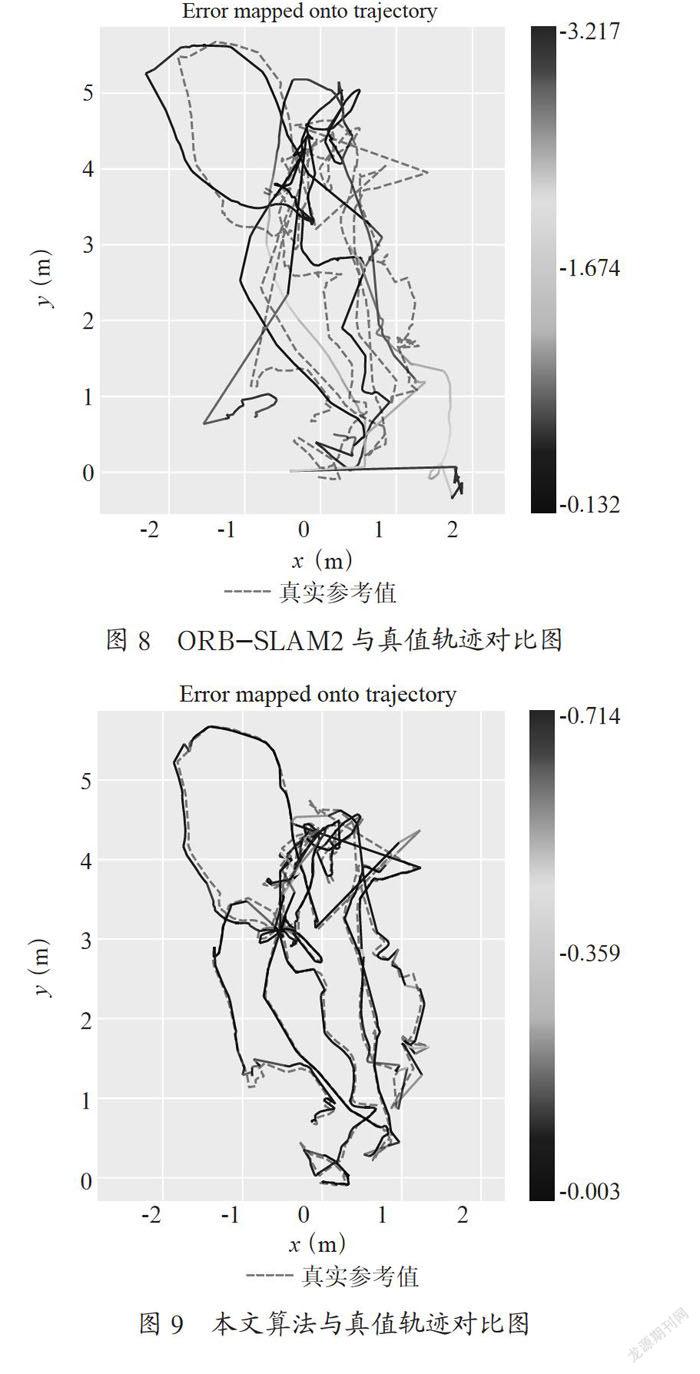
圖8與圖9分別將ORB-SLAM2算法和本文融合算法估計的二維軌跡與真實軌跡進行對比，兩圖中灰色虛線均表示地面真實參考值，彩色線分別表示ORBSLAM2的軌跡與本文融合算法的軌跡，由藍到紅的顏色過渡條表示軌跡絕對誤差的大小。由圖可以更直觀地看出跟蹤丟失路段的估值已得到較好地修正，本文算法估計的整體軌跡更靠近真實軌跡。

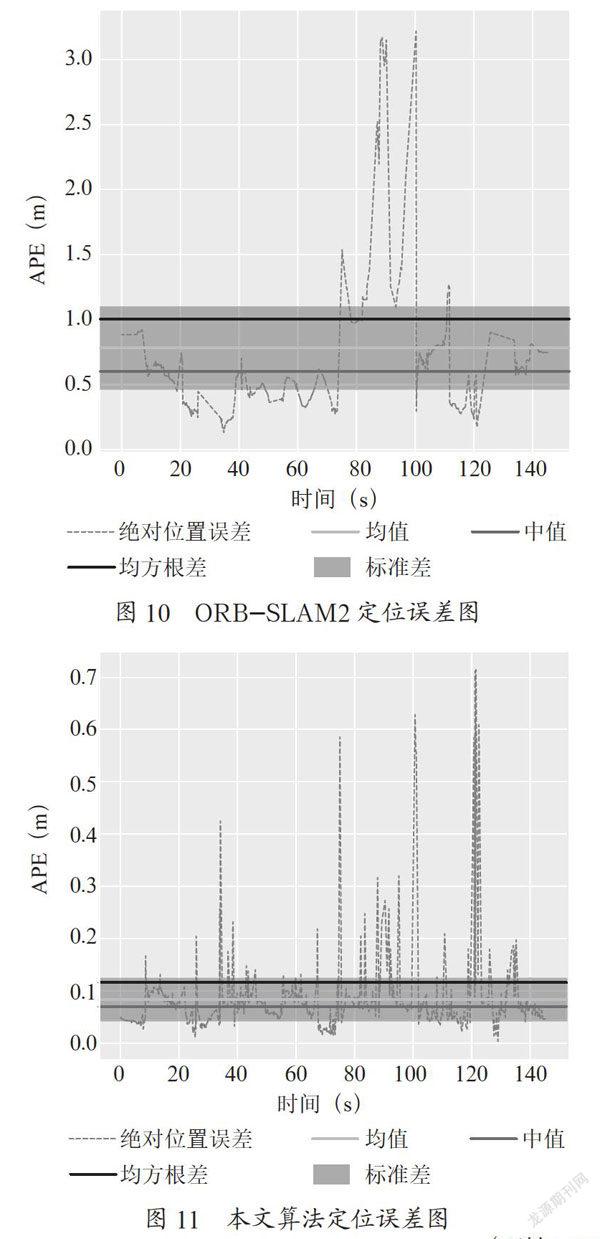
采用計算絕對位姿誤差的方式來驗證軌跡的全局一致性，對兩種算法的定位誤差進行評定及分析，定位誤差如圖10、圖11所示，ORB-SLAM2算法的定位誤差在跟蹤丟失時最大誤差達3.22 m，整個運動過程中最小誤差0.13 m，均值0.78 m，均方根誤差1.0 m，利用本文的方法進行融合校正之后跟蹤丟失問題得到有效解決，定位誤差最大為0.71 m，最小誤差0.003 m，均值0.08 m，均方根誤差0.11 m，各項誤差參數均表明，本文提出的算法定位精度有效提升，方法具有可行性。

4 ?結 ?論

本文提出了一種基于ROS開發的視覺慣性融合定位算法，解決了ORB-SLAM2算法在低性能計算平臺上因計算能力不足出現的ORB特征跟蹤丟失問題。本文首先建立了IMU誤差模型與視覺觀測誤差模型，并將視覺信息與IMU信息進行空間同步，最后利用卡爾曼濾波估計出位姿誤差，將誤差反饋到系統中進行位姿更新。經數據集驗證分析表明，本文提出的融合算法具有可行性，在定位精度和魯棒性上均有效提高。未來的工作包括：輕量化視覺部分，減輕CPU計算負擔，從根本上提高系統的可靠性。

參考文獻：

[1] 楊觀賜，王霄遠，蔣亞汶，等.視覺與慣性傳感器融合的SLAM技術綜述 [J].貴州大學學報（自然科學版），2020，37（6）：1-12.

[2] ENGEL J，KOLTUN V，CREMERS D. Direct Sparse Odometry [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2018，40（3）：611-625.

[3] MUR-ARTAL R，TARDóS J D. ORB-SLAM2：AnOpen-Source SLAM System for Monocular，Stereo，and RGB-D Cameras [J].IEEE Transactions on Robotics，2017，33（5）：1255-1262.

[4] 黃劍雄，劉小雄，章衛國，等.基于視覺/慣導的無人機組合導航算法研究 [J].計算機測量與控制，2021，29（2）：137-143+149.

[5] 杜小菁，陳洪，王欣，等.基于SINS解算的行人導航技術發展綜述 [J].戰術導彈技術，2020（1）：113-120.

[6] 孟春見，李開龍，張夢得.捷聯慣性基組合導航濾波算法比較研究 [J].電光與控制，2020，27（2）：18-21.

作者簡介：孫希君（1997—），女，漢族，山東武城人，碩士研究生在讀，研究方向：傳感器融合定位、組合導航。