基于改進FastICA的雷達信號分離方法
王國濤,姜秋喜,劉方正
(國防科技大學電子對抗學院,安徽 合肥 230037)
0 引言
隨著LPI雷達信號的廣泛應用,戰場電磁環境愈來愈密集復雜,給雷達信號的分選帶來了極大的威脅。傳統的信號分選系統主要利用信號的脈沖重復間隔(PRI)、到達時間(TOA)、到達角(DOA)、載頻(CF)以及脈沖寬度(PW)等輻射源描述字(EDW)來完成信號的分選識別,而LPI雷達使用具有寬頻帶和大時寬的信號,使空間電磁信號在時域大量交疊,頻域上跨度增大,受噪聲和強信號的影響,弱信號難以被檢測出來,密集復雜的電磁環境使得傳統算法難以準確地完成信號的分選[1-2]。
獨立成分分析技術(independent component analysis, ICA)是一種基于統計數據中尋找內在獨立因子或成分的方法。該方法能夠在變量和混合系統均未知的情況下,通過對觀測信號的分解得到隱藏在其中統計獨立的若干變量[3],FastICA算法是其中運行效率較高的一種算法,目前在生物信號處理[4]、語音信號分離[5]、無線通信[6]和數據挖掘[7]等領域都有廣泛的應用。傳統FastICA算法是基于二階牛頓迭代方法,進行合理近似的一種算法。為了提高FastICA算法的穩定性,減少迭代次數,近年來許多學者提出了改進的FastICA算法[8-11]。其中文獻[11]基于3階牛頓迭代法提出了改進的FastICA算法,其收斂速度快于傳統算法。為了解決基于輻射源描述字的傳統信號分選方法難以適應當前復雜電磁環境的問題,本文提出將基于3階牛頓迭代的改進FastICA算法應用于雷達信號的分離中。首先采用主成分分析(PCA)技術對信號數據進行降維預處理,然后利用改進算法進行循環迭代得到分離矩陣,最后根據分離矩陣提取出獨立的雷達信號成分。
1 改進的FastICA算法
FastICA算法需要對信號的非高斯性進行衡量,以確定最大值。目前主要衡量方法有峭度和負熵兩大類,由于峭度對野值比較敏感,容易造成大的偏差,所以本文使用負熵作為衡量工具,隨機變量x的負熵表達式為:
J(x)=H(x)-H(xgauss)
(1)
J(x)∝{E[G(x)]-E[G(xgauss)]}2
(2)
式(2)中,G(x)是x的非線性函數,常見G函數有3種,詳細見文獻[3]。
假設x=wTv是待估計的源信號(w是分離矩陣W中列向量,v是經過預處理后的觀測矩陣),那么根據非線性規劃中Kuhn-Tucke最優化條件,當分離矩陣W=[w1,w2,…,wm]中列向量的二范數為1,即‖wi‖2=1,i=1,2,…,m時,問題就轉化為求解最優化模型:
(3)
為求解該公式,建立拉格朗日函數:
L(w,β)=J(w)-β(‖w‖2-1)=
{E[G(wTv)]-E[G(xgauss)]}2+β‖w‖2
(4)
對式(4)求導,得到:
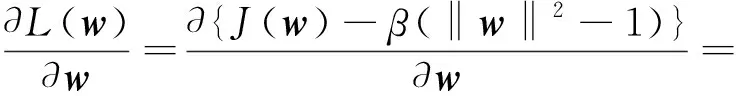
(5)
那么模型(3)的最大值求解問題可以轉化為求解下式:
(6)
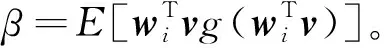
根據3階牛頓迭代法[12]:
(7)
xn+1是非線性方程f(x)=0的解,據此求解方程(3),再化簡得到改進的FastICA算法的迭代式為:
(8)
2 基于改進FastICA算法的雷達信號盲分離
圖1是雷達信號盲源分離的模型,假設有m個相同的傳感器任意分布在同一平面上,組成接收陣列。n個獨立的雷達源信號s1(t),s2(t),…,sn(t),在空間經過線性混疊后被接收陣列截獲,收到的信號為x1(t),x2(t),…,xm(t)。
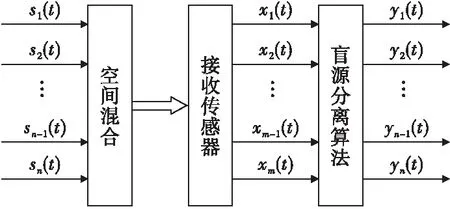
圖1 雷達信號盲源分離模型Fig.1 Blind source separation model of radar signal
混合模型可表示為:
(9)
式(9)中,aij是混合系數,為常數。該模型用矩陣可以表示為:
X=AS
(10)
式(10)中,S=[s1(t),s2(t),…,sn(t)]表示源信號矩陣,X=[x1(t),x2(t),…,xm(t)]表示觀測信號矩陣,A∈Rm×n表示混合矩陣。該模型必須具備以下條件[13]:
1) 所有源信號之間是相互統計獨立的。
2) 源信號中最多有一個是服從高斯分布的信號。
3) 觀測的混合信號個數應不小于源信號的個數,即m≥n。
在以上條件約束下,ICA算法要解決的問題就是:通過求取分離矩陣W,使得通過分離算法Y=WX后,輸出的矩陣Y中各分量相互獨立。
2.1 基于PCA的數據預處理
在使用FastICA算法前,為了提高運算效率,需要對觀測數據進行預處理。主成分分析(PCA)是對數據統計分析,提取數據間的特征,進行數據壓縮的經典方法。使用PCA方法可以從一組多維數據中找到冗余度更小的一個子集,對觀測數據進行降維,從而提高FastICA算法的效率。假設有一組數據X∈Rm×n,PCA變換過程如下:
1) 去均值。將矩陣X中的每一行減去該行的均值,即:
X←X-E(X)
(11)
2) 求數據的協方差矩陣:
CX=E[XXT]
(12)
式(12)中,CX是數據X的協方差矩陣。
3) 求協方差矩陣的特征值和對應的特征向量,特征值從大到小記為{d1,d2,…,dn},對應的特征向量為{u1,u2,…,un}。
4) 選取最大的m個特征值所對應的特征向量組成矩陣Wh={u1,u2,…,um}。
5) 對矩陣X進行變換:
(13)
式(13)中,V∈Rm×n是經過PCA處理后的數據矩陣。
2.2 算法流程
2.1節中算法過程只估計了一個獨立分量,要想分離所有變量則需要多次迭代,而且每次估計出分量后還應對分離矩陣進行處理,去除已分離變量,具體算法流程如下:
1) 數據預處理:對觀測信號進行去PCA處理,得到矩陣V=[v1,v2,…,vn]。
2) 初始化分離矩陣W=[w1,w2,…,wn],初始值可以為隨機值,但需滿足‖wi‖=1,i=1,2,…,n。
3) 根據迭代公式(5),更新wi,得到分離向量。
4) 每次迭代后對wi進行正交和歸一化處理,正交化采用對稱正交化算法。過程公式如下:
(14)
5) 判斷wi是否收斂,若式|wk+1-wk|<ε(本文取ε=10-7,k代表是第k次迭代結果)成立,則wi收斂;否則返回步驟3)繼續進行迭代。
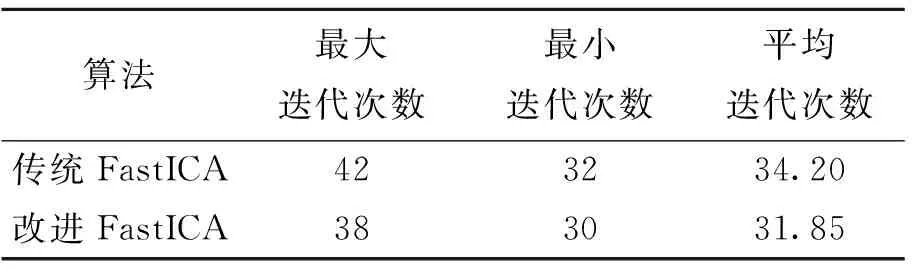
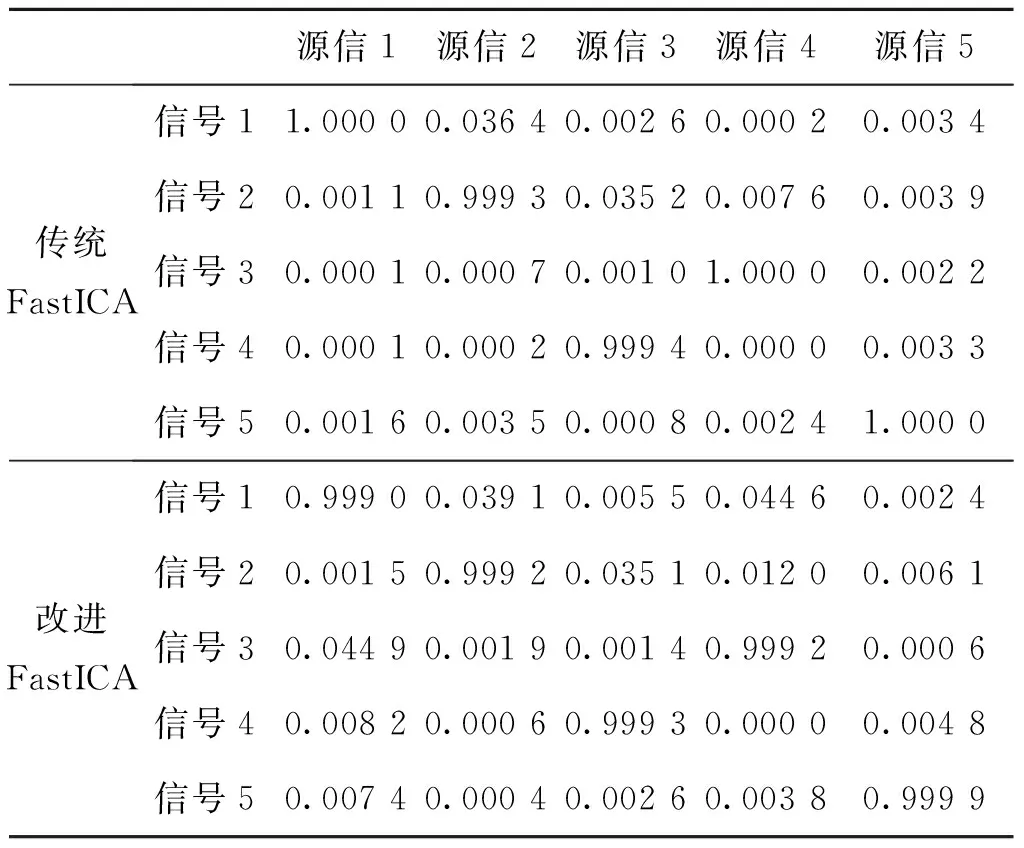
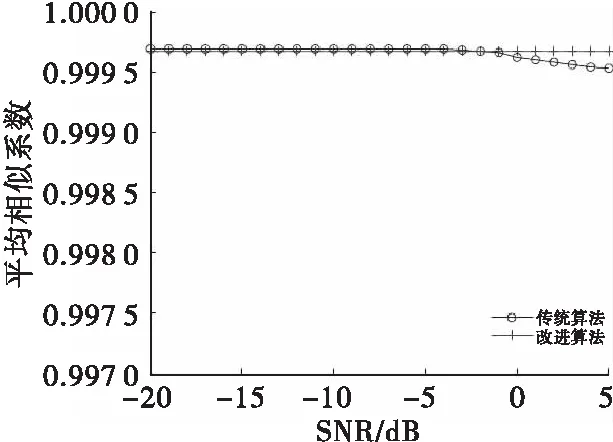
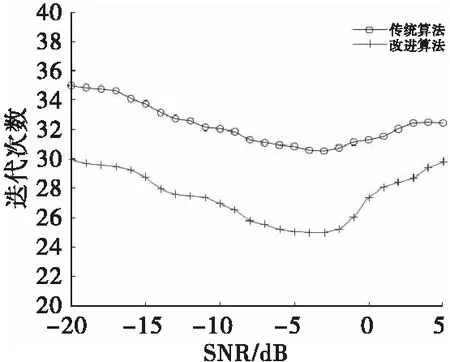
6) 若i 為了能夠評估改進FastICA算法分離信號的性能,這里選取信號的相似系數來對算法分離效果進行評價。相似系數是描述估計信號與源信號之間相似性的一種參數,定義為: (15) 式(15)中,si(t)為源信號中第i個信號序列,yj(t)為分離得到第j個信號序列。當兩信號獨立時,ξij=0;當yj(t)=csi(t),c為常數時,即兩個信號只是幅度不同時,ξij=1;ξij值越大表示兩個信號的一致性越好,算法的分離效果就越好[14]。 實驗仿真分兩組進行,實驗1為連續波信號的分離;實驗2為脈沖波信號的分離。分別使用本文中改進的算法和文獻[13]中傳統算法對信號進行分離實驗,并從估計的一致性和算法的收斂性兩個方面對實驗結果進行分析。 本組實驗分析的是連續波環境下的信號分離性能,設置了3組不同調制的連續波雷達信號和1組噪聲信號,分別是: 1) 單載頻信號(NS): s1=2cos(2πf0t) (16) 式(16)中,載頻f0=8×106Hz。 2) 線性調頻信號(LFM): s2=cos(2πf0t+kπt2) (17) 式(17)中,f0=107Hz,k=1012。 3) 二相編碼信號(BPSK):選取7位巴克碼,碼元內信號為cos(2πf0t+φ),碼元為1時,φ=π;碼元為0時,φ=0 ;載頻f0=8×106Hz。 4) 高斯白噪聲,噪聲功率為10 dBW,LFM信號對應的信噪比為-13 dB。 源信號波形如圖2所示,圖中信號從上至下依次對應為上述列舉的信號(1-4)。使用Matlab產生一組隨機的5×4的混合矩陣,混合后的信號時域波形如圖3所示。 圖2 連續波源信號的時域波形Fig.2 The continous source signals 圖3 混合信號的時域波形Fig.3 The mixed signals 分別使用兩種算法對信號進行分離,圖4、圖5分別是改進算法和傳統算法分離得到的波形圖。表1為分離得到信號與源信號之間的相似系數矩陣,表中源信1-4分別代表源信號中對應的信號(1-4),信號1-5分別對應圖4、圖5中從上至下的5個信號。表2是經過100次實驗后總迭代次數的統計表。 圖4 改進算法分離信號的時域波形Fig.4 The signals separated by the improved algorithm 圖5 傳統算法分離信號的時域波形Fig.5 The signals separated by traditional algorithm 表1 分離信號與源信號的相似系數統計表Tab.1 Statistical table of similarity coefficient between separated signal and source signal 估計的一致性方面:從表1中可以看出雖然輸入為4組信號,輸出為5組信號,但是輸出信號中有一組幅度明顯遠遠小于其他組,因此可以認為該信號不存在;從波形圖和表1可以看出,改進FastICA算法分離出的信號與源信號非常相近,只是排列順序與源信號不同,而且某些信號的幅度與對應信號的幅度也有所不同,分離出的信號與源信號的相似度均達到0.999 0以上。通常把分離信號順序和幅度的不確定性稱為盲源分離問題的不確定性,這些對后續信號的參數測量或者分類識別并不影響。而且如果把白噪聲看作是強噪聲干擾信號,該算法也能正確分離出噪聲信號,這對于判斷干擾信息也有實際的意義。 算法的收斂性方面:從表2可以看出,改進算法總體上是收斂的,表明算法分離不同調制信號是可行的。同時改進算法雖然偶爾的迭代次數較多,但總體上要少于傳統算法,因此收斂性更好。 表2 兩種算法總迭代次數統計表Tab.2 Statistics of total iterations of the two algorithms 本組實驗分析的是對脈沖信號的分離能力,實驗中設置了到達時間相同、寬脈沖覆蓋窄脈沖、PRI隨機以及噪聲干擾等特殊情況,以此檢驗算法的性能。實驗中包含3組脈沖信號和2組連續信號:3組脈沖信號中第一組脈寬(PW)和脈沖重復周期(PRI)固定,第二組PW和PRI隨機變化,第三組PW固定,PRI隨機;連續信號中一組為BPSK信號,另一組為模擬強高斯白噪聲干擾信號。信號參數設置如下: 1) 單載頻脈沖:載頻f0=8×106Hz;脈沖寬度PW=5 μs,脈沖重復周期PRI=20 μs。 2) 線性調頻脈沖:初始頻率f0=107Hz,調頻斜率k=1 012,PW={6.4,6,4,6,5,8,10,7} μs, PRI={16.4,14.2,12,19,17,20,21.4} μs。 3) 頻率編碼信號:信號中兩個頻率分別為f1=6×106Hz,f2=9×106Hz,PW=6 μs,PRI={21,22,24,27,21} μs。 4) 二相編碼信號(BPSK):本組信號設置為連續信號,選取序列為{1,1,1,0,0,1,0}的7位巴克碼信號,碼元內信號載頻f0=107Hz。 5) 高斯白噪聲:噪聲功率為20 dBW,信號2對應的信噪比為-27.3 dB。 源信號波形如圖6所示,信號從上至下依次對應列舉的信號(1-5)。本實驗的混合矩陣由Matlab隨機產生,得到的混合信號波形如圖7所示,從圖中可以看到信號幾乎完全被噪聲淹沒,無法從視頻信號中檢測出脈沖。 圖6 脈沖源信號的時域波形Fig.6 The pulse source signals 圖7 混合信號的時域波形Fig.7 The mixed signals 采用兩種算法對脈沖信號進行分離,得到的時域波形分別如圖8、圖9所示。表3為對應的相似系數統計表。表4為本實驗進行100次得到的總迭代次數的統計表。 表4 兩種算法總迭代次數統計表Tab.4 Statistics of total iterations of the two algorithms 圖8 改進算法分離信號的時域波形Fig.8 The signals separated by the improved algorithm 估計的一致性方面:從分離的波形圖可以看出,改進算法分離得到的信號與源信號非常接近,只是信號的排列順序不一致。與實驗1類似,表3中源信1-5分別代表源信號中對應的信號(1-5),信號1-5分別對應圖8、圖9中從上至下的5個信號,表中每行每列中只有一個值為1或者接近于1,其他為0或者接近于0,可見分離得到的信號幾乎完整地保留了源信號的所有信息,說明該算法對同時到達、寬脈沖覆蓋窄脈沖、PRI隨機等脈沖雷達信號具有很好的分離效果,而且當把混合信號中的噪聲當作是有意干擾信號時,也能單獨分離出來。對比兩種算法的相似系數可以看出,改進算法分離效果與傳統算法相差不大。 圖9 傳統算法分離信號的時域波形Fig.9 The signals separated by the traditional algorithm 表3 分離信號與源信號的相似系數統計表Tab.3 Statistical table of similarity coefficient between separated signal and source signal 算法的收斂性方面:改進算法在分離信號時收斂,表明了該算法在雷達系統信號分選中的可行性。與實驗1類似,實驗中改進算法迭代次數總體較小,收斂速度優于傳統算法。 為了進一步驗證算法的抗噪性能,在3.2節的實驗信號環境下,信噪比設置在-20~5 dB范圍內進行蒙特卡洛實驗。每隔1 dB進行200次蒙特卡洛實驗,得到的仿真結果如圖10和圖11所示。 圖10 相似系數隨信噪比變化曲線Fig.10 Variation curve of similarity coefficient with SNR 實驗中將源信號對應的最大相似系數進行平均,使用平均相似系數來衡量算法的分離效果。圖10為信號的平均相似系數隨信噪比變化曲線,圖11為算法總迭代次數隨信噪比變化曲線。由實驗結果可知,即使在較低信噪比條件下,算法仍具有較好分離效果。算法總迭代次數在不同信噪比條件下浮動范圍很小,改進算法收斂速度優于改進前算法。 圖11 總迭代次數隨信噪比變化曲線Fig.11 Variation of iterations number with SNR 綜合文中兩組實驗,總結如下: 1) 算法可以分離不同調制的雷達信號,可以分離出PRI隨機變化的雷達信號,較基于輻射源描述字的傳統算法有一定的優勢。 2) 算法可以實現到達時間相同、寬脈沖覆蓋窄脈沖以及強噪聲干擾等復雜電磁環境下的雷達信號分選,而且分離出信號的信息與源信號基本相同。 3) 改進算法較傳統FastICA算法在分離效果相同的情況下,運算迭代次數更少,具有更快的收斂速度。 本文在深入研究FastICA算法原理的基礎上,提出基于改進FastICA算法的雷達信號分離方法。該方法利用了PCA進行數據預處理,降低了數據的維數;進而采用改進的3階迭代公式進行循環迭代,提取出獨立的源信號,達到雷達信號分離的目的。實驗結果表明,該方法能夠在復雜的電磁環境中有效地分離出源信號,相較于傳統FastICA算法,該方法具有更快的收斂速度。這對于雷達偵察系統的信號預分選有一定的參考意義。2.3 算法性能評價指標
3 仿真實驗及結果分析
3.1 連續波信號分離實驗
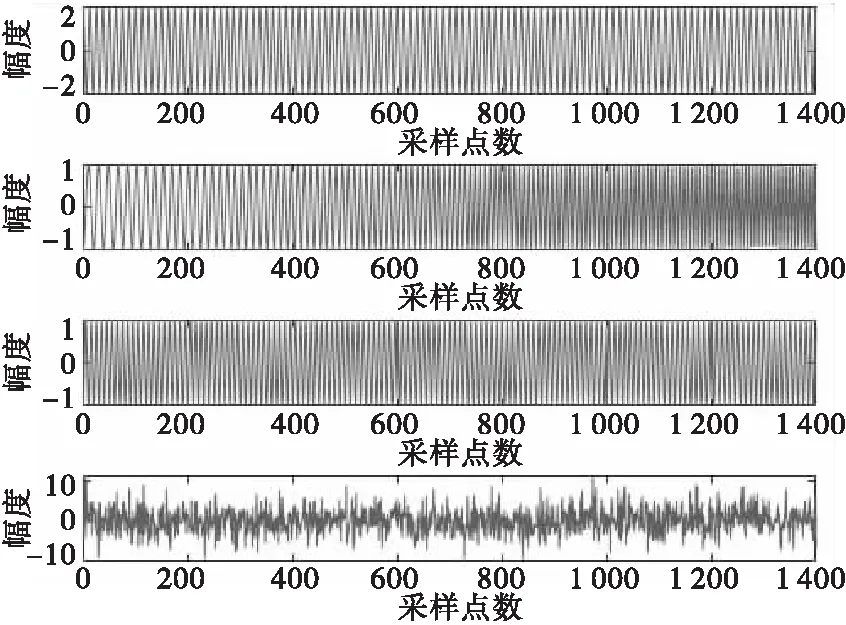
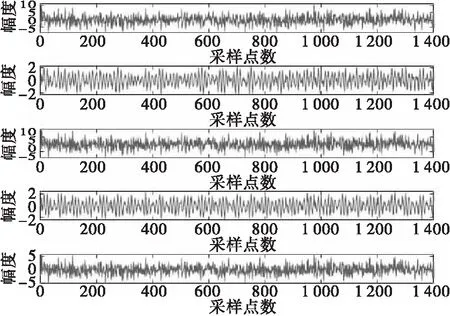
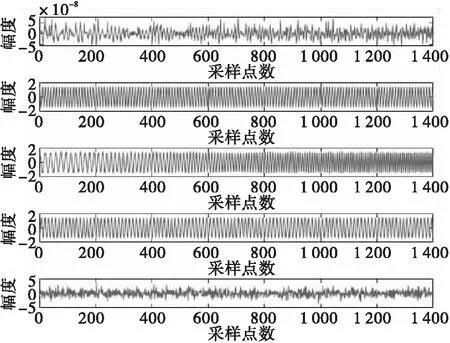
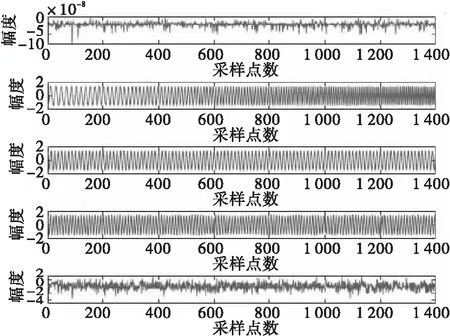
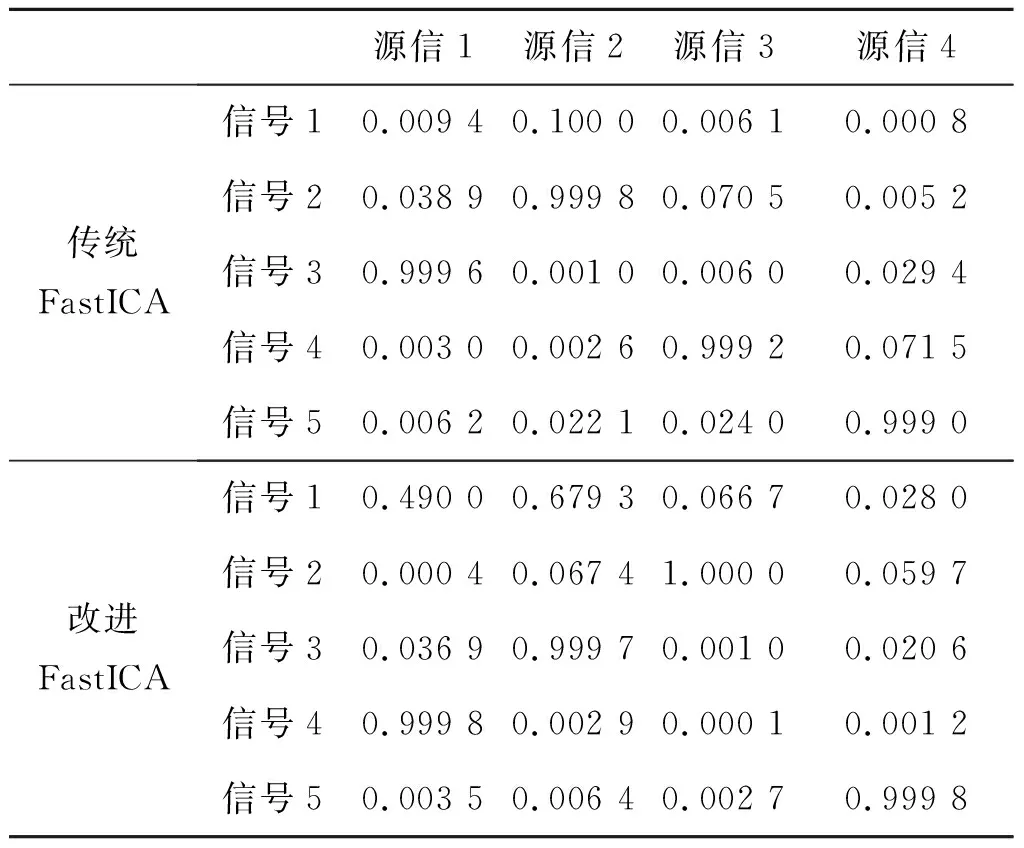

3.2 脈沖波信號分離實驗




3.3 不同信噪比條件下算法的性能
3.4 實驗總結
4 結論

