泡沫瀝青油水混合過程的分子動(dòng)力學(xué)研究
趙鑫元,劉 云,柏 林
(河海大學(xué)道路與鐵道工程研究所,江蘇 南京 210098)
泡沫瀝青中水分的存在能夠使泡沫瀝青在較低的溫度下施工,與熱拌瀝青相比,泡沫瀝青在節(jié)能、環(huán)保、施工等方面有著明顯的優(yōu)勢(shì)。
泡沫瀝青中水分對(duì)其路用性能的影響引起了許多學(xué)者的關(guān)注[1-3]。 姚柒忠[4]對(duì)泡沫瀝青混合料的用水量進(jìn)行研究,發(fā)現(xiàn)泡沫瀝青中水的含量會(huì)對(duì)瀝青分散性狀和分布均勻程度產(chǎn)生影響。 奎永才等[5]通過瀝青發(fā)泡試驗(yàn)就發(fā)泡用水量對(duì)發(fā)泡效果的影響進(jìn)行研究,得出瀝青發(fā)泡的最佳用水量為2%。 楊新格[6]通過動(dòng)態(tài)剪切流變?cè)囼?yàn)研究發(fā)泡用水量對(duì)泡沫瀝青溫度敏感性的影響,認(rèn)為發(fā)泡用水量增大泡沫瀝青溫度敏感性提高。 朱林等[7]研究了發(fā)泡用水量對(duì)泡沫瀝青高溫流變性能的影響,發(fā)現(xiàn)當(dāng)用水量增大,泡沫瀝青的高溫性能呈現(xiàn)出先提高后降低的變化規(guī)律, 在用水量1%~2%泡沫瀝青的抗高溫性越好。 然而,現(xiàn)有對(duì)泡沫瀝青的研究多集中于室內(nèi)物理試驗(yàn),無(wú)法很好地展現(xiàn)瀝青與水分之間相互結(jié)合、相互作用這一微觀過程。
1 模型的建立及驗(yàn)證
1.1 基質(zhì)瀝青分子模型的建立
采用Li 等提出的4 組分分析法[12-14],將瀝青分為瀝青質(zhì)、膠質(zhì)、芳香分和飽和分4 個(gè)組分。 在MS建模中,用4 組分分析法建立的分子模型性質(zhì)更加接近實(shí)際而且更容易分析瀝青中各組分的性質(zhì)。 許多學(xué)者已經(jīng)對(duì)瀝青進(jìn)行分析并提出了合理的分子模型[15-18],表1 給出了各組分模型,其中白色為H 原子,灰色為C 原子,紅色為O 原子,藍(lán)色為N 原子,黃色為S 原子。瀝青各組分分子數(shù)量之比為瀝青質(zhì)∶膠質(zhì)∶芳香分∶飽和分=5∶3∶42∶11。根據(jù)各組分的比例,在MS 軟件中的Amorphous Cell 模塊建立體積為3.21 nm × 3.21 nm × 3.21 nm 的基質(zhì)瀝青大分子模型(圖1)。
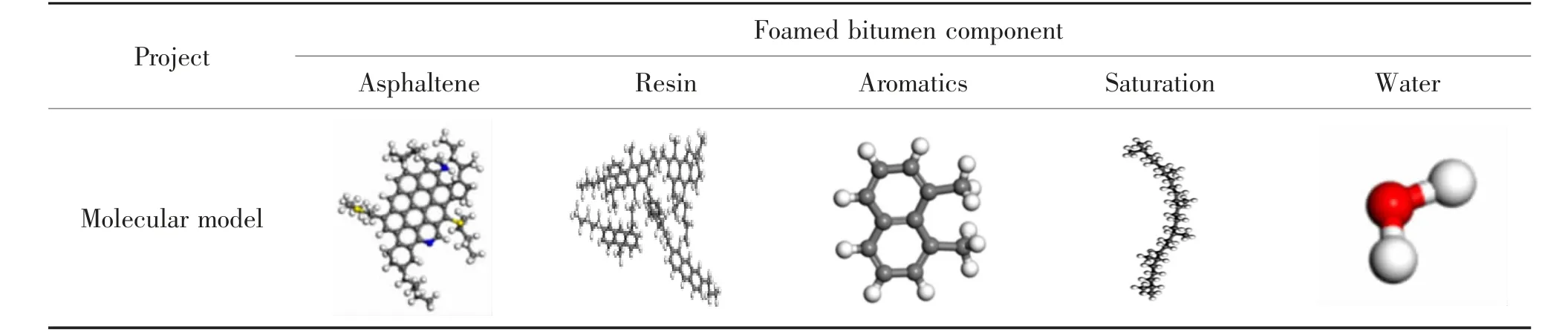
表1 各組分模型Tab.1 Models of components
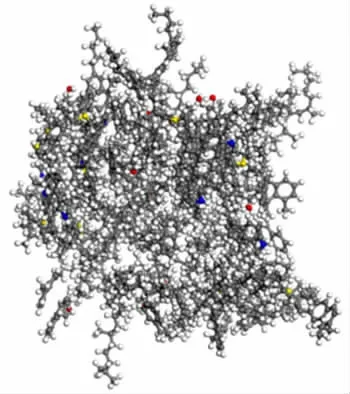
圖1 基質(zhì)瀝青模型Fig.1 Model of the asphalt
1.2 基質(zhì)瀝青分子模型的驗(yàn)證
1) 為了使建立的模型更加接近實(shí)際, 用Discover 模塊對(duì)模型進(jìn)行優(yōu)化,優(yōu)化后的基質(zhì)瀝青分子模型的密度為0.997 98 kg/m3,與瀝青實(shí)際密度1 kg/m3相接近,建立的模型與實(shí)際情況有良好的相關(guān)性。
2) 在實(shí)際瀝青中,瀝青質(zhì)占比在19%~31%,膠質(zhì)在16%~26%[19]。 模型各組分參數(shù)見表2,均在范圍內(nèi)。
3) Redelius 以溶解度參數(shù)作為研究材料相溶性的評(píng)價(jià)指標(biāo)[20],本文采用溶解度參數(shù)驗(yàn)證模型中分子的相溶性。 在Analyse 模塊中計(jì)算得到各個(gè)分子的溶解度參數(shù),結(jié)果如表2 所示,根據(jù)計(jì)算結(jié)果看出各組分分子溶解度參數(shù)相差較小,模型結(jié)構(gòu)穩(wěn)定。
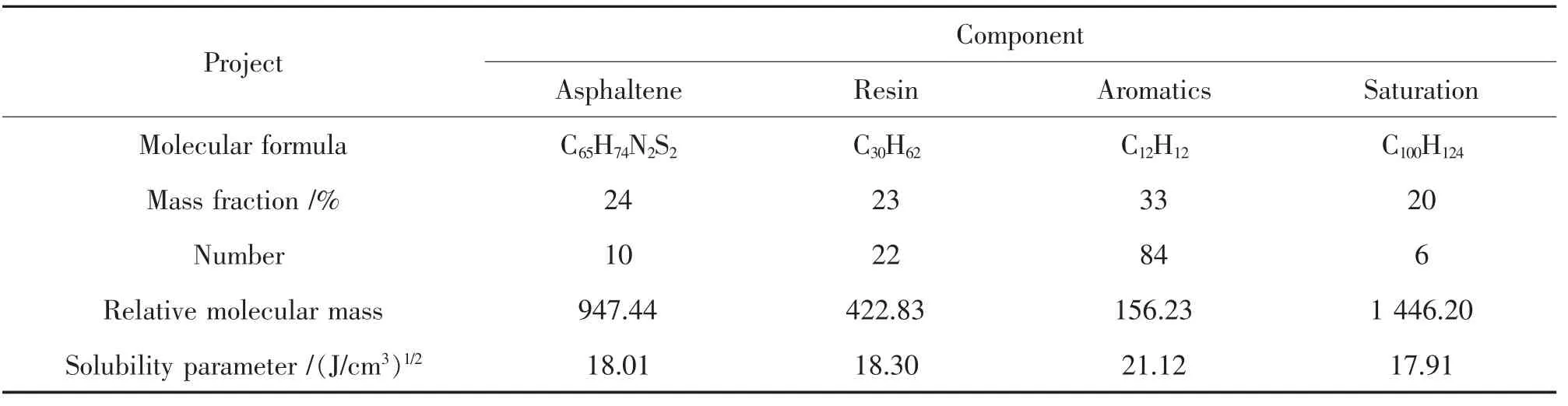
表2 基質(zhì)瀝青分子的組成Tab.2 Composition of asphalt molecule
2 分子動(dòng)力學(xué)模擬
2.1 模擬力場(chǎng)介紹
COMPASS 力場(chǎng)是為了研究非鍵能參數(shù)而通過經(jīng)驗(yàn)方法開發(fā)出的一種新的力場(chǎng)[21],適用于高分子有機(jī)物的分析研究, 故本文選取COMPASS 力場(chǎng)進(jìn)行模擬計(jì)算,其函數(shù)形式如式(1)所示。
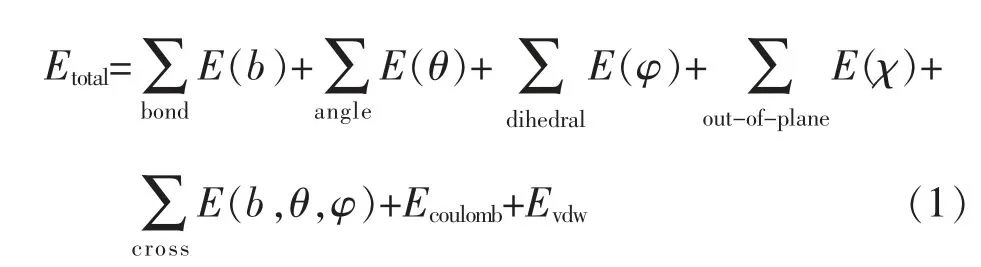
式中: 前5 項(xiàng)為成鍵的相互作用,E (b),E(θ),E(φ),E(χ)分別為鍵長(zhǎng)、鍵角、二面角和距平面角度的內(nèi)部相互作用;E(b,θ,φ)為鍵長(zhǎng)、鍵角和二面角之間的相互作用;Ecoulomb為靜電相互作用;Evdw為范德華作用能,計(jì)算公式如下
隨著現(xiàn)代信息技術(shù)的不斷發(fā)展,隨著科學(xué)技術(shù)的不斷進(jìn)步,現(xiàn)代信息技術(shù)能夠?yàn)槠髽I(yè)的財(cái)務(wù)風(fēng)險(xiǎn)預(yù)警機(jī)制提供技術(shù)支持。企業(yè)通過構(gòu)建科學(xué)而完善的財(cái)務(wù)風(fēng)險(xiǎn)預(yù)警機(jī)制,幫助企業(yè)經(jīng)營(yíng)者和管理者在財(cái)務(wù)管理中獲得一個(gè)較為清晰的、可靠的、準(zhǔn)確的參考數(shù)據(jù)和控制標(biāo)準(zhǔn),從而對(duì)企業(yè)的財(cái)務(wù)管理工作起到一定的引導(dǎo)和指導(dǎo)作用。

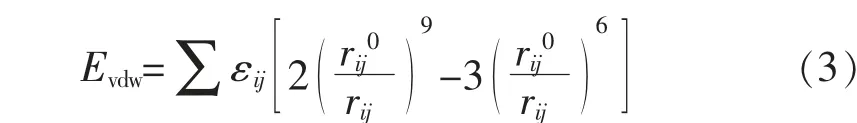
式中:i,j 分別表示不同原子;q 為原子電荷;r0為兩原子間初始距離;r 為兩原子間距離;ε 為勢(shì)阱深度。
2.2 模擬參數(shù)的確定
為研究不同用水量的泡沫瀝青油水混合過程,首先建立泡沫瀝青油水分離模型, 通過Build layer模塊將優(yōu)化過后的基質(zhì)瀝青分子模型放在同一個(gè)晶胞中,在基質(zhì)瀝青分子之間添加水分子。水分子的數(shù)量是按照泡沫瀝青發(fā)泡用水量決定的,泡沫瀝青中水分占1%~4%,水分子數(shù)量見表3。 圖2 為模擬前的油水分離模型, 在COMPASS 力場(chǎng)下采用非周期邊界條件對(duì)油水分離模型進(jìn)行分子弛豫。 分子動(dòng)力學(xué)運(yùn)算選擇NPT 系綜, 模擬步數(shù)設(shè)置為200 000步,模擬時(shí)間為200 ps,壓強(qiáng)為0.1 MPa,每5 000步輸出一個(gè)構(gòu)象。 在模擬過程中,瀝青分子逐漸將水分子包裹,最終形成穩(wěn)定的泡沫瀝青模型,如圖3所示。

表3 模型中的水分子數(shù)量Tab.3 Quantity of water molecules in model
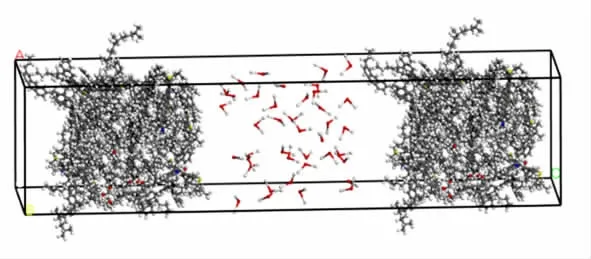
圖2 油水分離模型Fig.2 Asphalt-water separation model
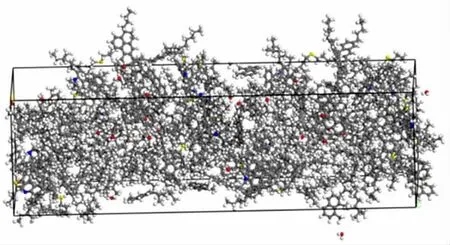
圖3 泡沫瀝青模型Fig.3 Foamed asphalt model
2.3 模擬結(jié)果與分析
泡沫瀝青完成后得到不同用水量泡沫瀝青在油水混合過程中能量的變化曲線,如圖4 所示。 在NPT 系綜下,0~50 ps 間能量下降明顯,這是由于在密度差的作用下分子逐漸向空隙運(yùn)動(dòng);在50~150 ps間模型能量下降速率變緩,說明模型中的空隙基本填充完畢;在150 ps 后能量變化逐漸穩(wěn)定最終處于平衡的位置說明油水混合逐漸完成。

圖4 不同用水量泡沫瀝青能量變化曲線Fig.4 Energy curves of foamed asphalt with different water content
2.3.1 各組分的擴(kuò)散系數(shù)
擴(kuò)散系數(shù)計(jì)算公式可通過愛因斯坦關(guān)系式推導(dǎo)獲得。 愛因斯坦關(guān)系式幾何意義為擴(kuò)散系數(shù)是均方位移曲線斜率的1/6,公式如下
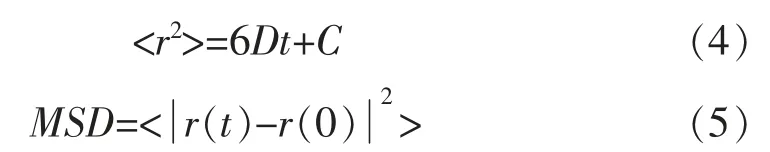
式中:
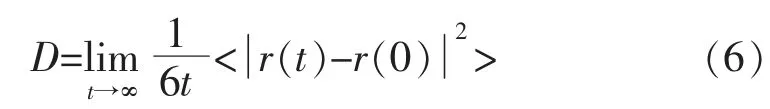
式中:< >為體系內(nèi)的原子平均值;r 為位移,即擴(kuò)散系數(shù)是均方位移的1/6。
由于MS 模擬軟件無(wú)法直接得出擴(kuò)散系數(shù),根據(jù)公式可知擴(kuò)散系數(shù)與均方位移有關(guān)。在Forcite 下的Analyse 模塊得到瀝青在油水混合過程中的均方位移變化曲線(圖5)。

圖5 不同用水量泡沫瀝青分子均方位移變化曲線Fig.5 MSD curves of foamed asphalt with different water content
通過對(duì)不同含水率下的泡沫瀝青均方位移曲線與時(shí)間數(shù)據(jù)擬合,結(jié)果如圖6 所示。

圖6 擬合后的不同用水量泡沫瀝青分子均方位移變化曲線Fig.6 MSD curves of foamed asphalt with different water content
根據(jù)計(jì)算結(jié)果能夠看出,0~150 ps 與150~200 ps的斜率相差較大, 根據(jù)能量變化曲線將兩段曲線分別定義為油水混合階段和油水混合完成后泡沫瀝青自擴(kuò)散階段。 根據(jù)能量變化曲線和均方位移變化曲線來(lái)看, 選擇0~150 ps 曲線斜率來(lái)計(jì)算油水混合過程的擴(kuò)散系數(shù)更為合理。 考慮到本文模型中分子數(shù)量多而復(fù)雜, 無(wú)法直接分析研究每一個(gè)分子的擴(kuò)散規(guī)律,在Edit set 模塊中,分別選中瀝青4 組分模型及水分子模型, 建立不同集合計(jì)算各組分的分子擴(kuò)散系數(shù),并在Analyse 模塊中輸出不同集合的均方位移變化曲線, 計(jì)算各個(gè)組分在0~150 ps 的斜率,并代入式(6),結(jié)果如圖7 所示。
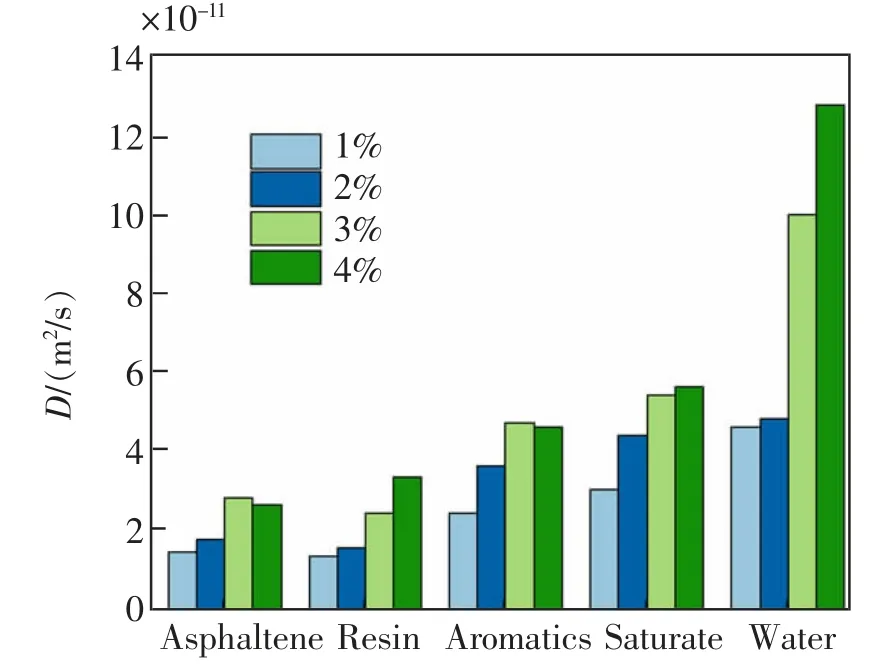
圖7 不同發(fā)泡用水量下泡沫瀝青各組分?jǐn)U散系數(shù)Fig.7 Diffusion coefficient of each component with different water content
擴(kuò)散系數(shù)越大說明分子運(yùn)動(dòng)越劇烈。 從計(jì)算結(jié)果能夠看出,泡沫瀝青各組份的擴(kuò)散系數(shù)隨著水分的增多有升高的趨勢(shì), 在用水量2%~3%之間,4 組分?jǐn)U散系數(shù)升高最明顯。 原因可能是水分子的增多使晶胞體積增大,各組分的擴(kuò)散系數(shù)由于晶胞體積增大而升高。 水分子在2%~3%之間擴(kuò)散系數(shù)也有明顯的增長(zhǎng),3%時(shí)水分子的擴(kuò)散系數(shù)是2%時(shí)的2倍左右。原因是水分子有很大的極性[22],會(huì)在有機(jī)物上發(fā)生聚集從而使水分子與有機(jī)分子的接觸面積增大,并在有機(jī)物內(nèi)部形成通道使水分子的擴(kuò)散系數(shù)有明顯的增加。
在相同的用水量下, 膠質(zhì)的擴(kuò)散系數(shù)最小,飽和分的擴(kuò)散系數(shù)最大,這是由于瀝青4 組分中芳香分和飽和分屬于分子量小的分子,混合過程中小分子運(yùn)動(dòng)劇烈所以擴(kuò)散系數(shù)較大。
2.3.2 水分子和基質(zhì)瀝青的相互作用
泡沫瀝青分子模型能夠分為基質(zhì)瀝青模型和水分子模型兩個(gè)部分, 所以基質(zhì)瀝青分子與水分子間的相互作用會(huì)對(duì)泡沫瀝青的穩(wěn)定性產(chǎn)生影響。 在油水混合過程中,基質(zhì)瀝青與水不產(chǎn)生化學(xué)反應(yīng),所以水分子和瀝青分子的相互作用能主要由非鍵能提供,水分子和基質(zhì)瀝青間的非鍵能計(jì)算公式如下
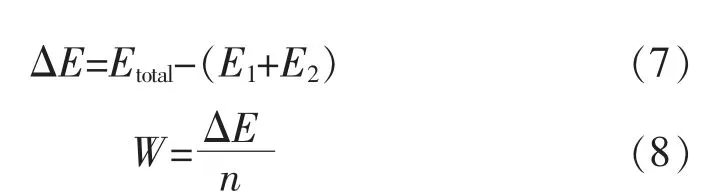
式中:△E 為相互作用能,kJ/mol;E1為瀝青分子的非鍵能,kJ/mol;E2為水分子的非鍵能,kJ/mol;Etotal為油水混合體系的非鍵能,kJ/mol;W 為單位水分子與瀝青的相互作用能,kJ/mol;n 為水分子數(shù)量。
若△E 為正值, 說明瀝青分子和水分子之間為排斥作用,反之吸引,體系穩(wěn)定。 通過Forcite 中的Energy 模塊能夠得到水分子、瀝青和油水混合體系的能量,代入式(7),結(jié)果如圖8 所示。 從模擬結(jié)果能夠看出在泡沫瀝青中水和瀝青之間具有排斥作用。 當(dāng)水分子增多,瀝青和水分子之間的排斥作用有增大的趨勢(shì)。 在相互作用中靜電力略大于范德華力。 根據(jù)式(8),計(jì)算每個(gè)水分子與瀝青之間的相互作用能,結(jié)果如表4 所示。
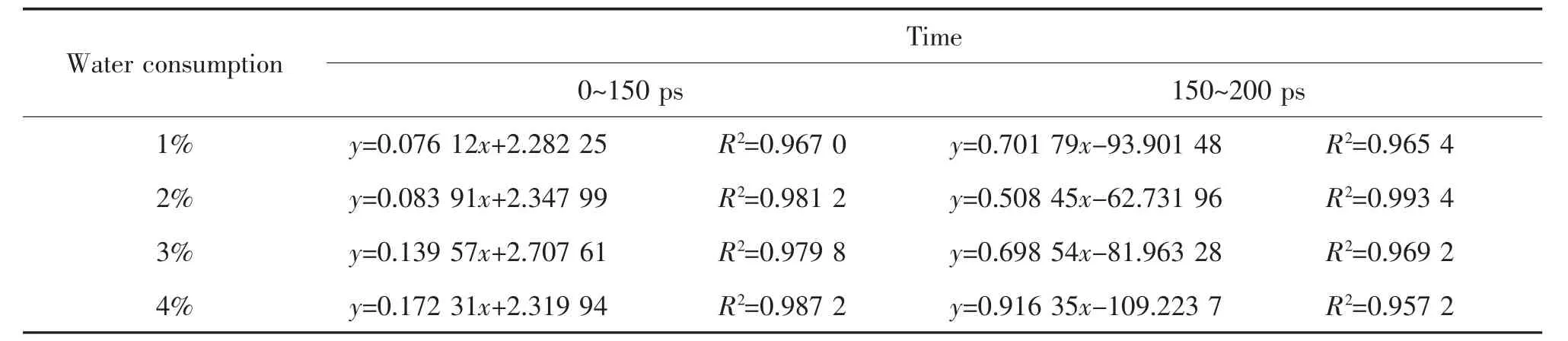
表4 擬合結(jié)果Tab.4 Fitting results
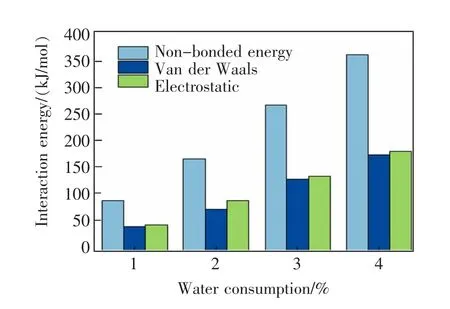
圖8 水分子和瀝青之間的相互作用能Fig.8 Interaction energy between water molecular and asphalt
由表4 可見,發(fā)泡用水量的變化對(duì)單位水分子與瀝青之間的排斥作用影響不大,單位水分子與瀝青分子之間的相互作用能在4.16 kJ/mol 左右。 泡沫瀝青中瀝青和水分子的排斥作用增大可能是瀝青和水分子之間的接觸面積增大導(dǎo)致的,過多的水分子會(huì)影響泡沫瀝青分子的穩(wěn)定性并降低泡沫瀝青分子模型的強(qiáng)度。

表5 單位水分子與瀝青的相互作用能Tab.5 Interaction energy between each water molecular and asphalt
2.3.3 泡沫瀝青模型中水分子的分布
泡沫瀝青發(fā)泡與內(nèi)部的水分有關(guān)。 在最后一幀油水混合模型選擇Analyse 模塊中的Relative concentration 得到水分子在泡沫瀝青中水平方向上的相對(duì)濃度曲線,如圖9 所示。
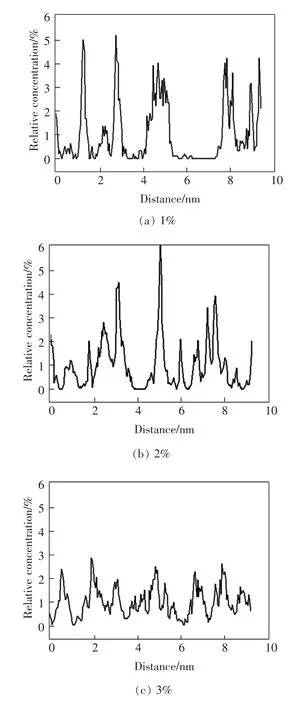
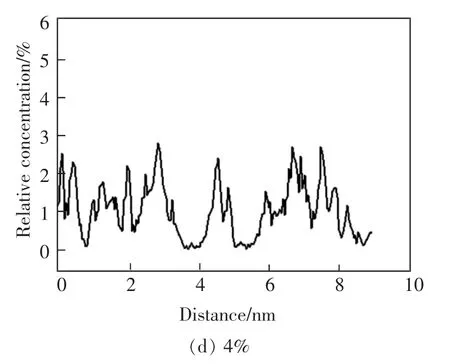
圖9 水分子的分布Fig.9 Distribution of water molecular
在油水分離模型中水分子加入的位置在距離原點(diǎn)5~6 nm 處。 在油水混合結(jié)束后,從水分子分布曲線能夠看出,發(fā)泡用水量為1%和2%時(shí),水分子相對(duì)濃度曲線波動(dòng)大。 用水量為3%和4%時(shí),與用水量小于3%的泡沫瀝青相比, 水分子的相對(duì)濃度曲線波動(dòng)較小。 能夠得到當(dāng)泡沫瀝青用水量大于3%時(shí)水分子較均勻地分布在泡沫瀝青模型當(dāng)中,發(fā)泡效果較好。
3 結(jié)論
1) 根據(jù)能量和均方位移變化曲線能夠看出泡沫瀝青油水混合過程主要發(fā)生在0~150 ps,150 ps之后是泡沫瀝青分子的自擴(kuò)散階段。 在泡沫瀝青油水混合過程中,水分子的加入導(dǎo)致各組分的擴(kuò)散系數(shù)增大。
2) 水分子與瀝青有機(jī)物之間為排斥作用,單位水分子的排斥作用受泡沫瀝青用水量變化影響不明顯,單位水分子與瀝青分子的相互作用能在4.16 kJ/mol 處浮動(dòng)。
3) 泡沫瀝青油水混合結(jié)束后,在發(fā)泡用水量小于3%的泡沫瀝青中水分子容易在泡沫瀝青中聚集,在發(fā)泡用水量大于3%時(shí),水分子較均勻分布在泡沫瀝青模型中,更利于泡沫瀝青中氣泡的形成。

