基于散射參數與差分進化算法的EMI噪聲源阻抗提取方法

馬 浩,裴亞康,趙 陽,張 成,孫逸群,周孟夏

(南京師范大學南瑞電氣與自動化學院,江蘇 南京 210023)

近年來,隨著開關電源高頻化和小型化的不斷發展,開關電源設備內部產生的傳導電磁噪聲越來越嚴重[1]. 采用EMI濾波器是抑制傳導電磁噪聲的有效手段,而噪聲源內阻抗的提取是開關電源EMI濾波器設計的關鍵.

傳統的噪聲源阻抗提取方法主要有:插入損耗(insertion loss,IL)法、電流探頭(current probe,CP)法和散射參數(scattering parameter,SP)法. IL法是通過在負載和EUT之間并聯或串聯一個標準阻抗來計算EUT阻抗,然后分別測量有無標準阻抗狀態下電路的總插入損耗. 但是,在實際應用中,當被測阻抗接近負載阻抗時,IL法的精度較低. 此外,在測量差模噪聲源阻抗時[2-3],易受被測電路中耦合電容的影響. 鑒于IL法的缺點,采用高頻電流探頭的CP法被提出,它可以計算有無噪聲源情況下的測試系統的總阻抗,然后通過簡單的減法獲得噪聲源阻抗. 但是,CP方法只能提取阻抗幅值,而無法獲得其相位[4-7]. 針對CP法存在的缺陷,采用雙電流探頭和矢量網絡分析儀(VNA)測量的SP法被提出. 在該方法中,VNA用于產生和接收高頻信號,同時分別獲取各測試狀態下信號檢測端口的信號注入參數、傳輸參數和反射參數. 最后通過計算獲得包括幅值和相位的EUT噪聲源阻抗信息,但該方法仍無法獲得EUT噪聲源內阻抗的等效RLC參數[8-13].

為了解決和克服傳統方法的缺點,本文提出了一種SP法與DE算法相結合的噪聲源阻抗提取方法. 首先對噪聲源進行建模,利用SP法獲得阻抗,然后建立阻抗的等效參數函數來處理其幅頻特性. 最后,利用DE算法進行全局最優求解,得到噪聲源的阻抗信息,包括振幅、相位等參數和等效RLC參數.

1 基于SP法的噪聲源阻抗建模

1.1 噪聲源阻抗定義

(1)

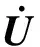
(2)

由于ω=2πf,Z的幅值和相位可以改寫為:

(3)

1.2 噪聲源阻抗模型

散射參數是射頻矢量參數,由兩個復數的比值定義,包含信號的幅值和相位信息. 散射參數可以描述網絡端口特性,評價反射信號和傳輸信號的特性.

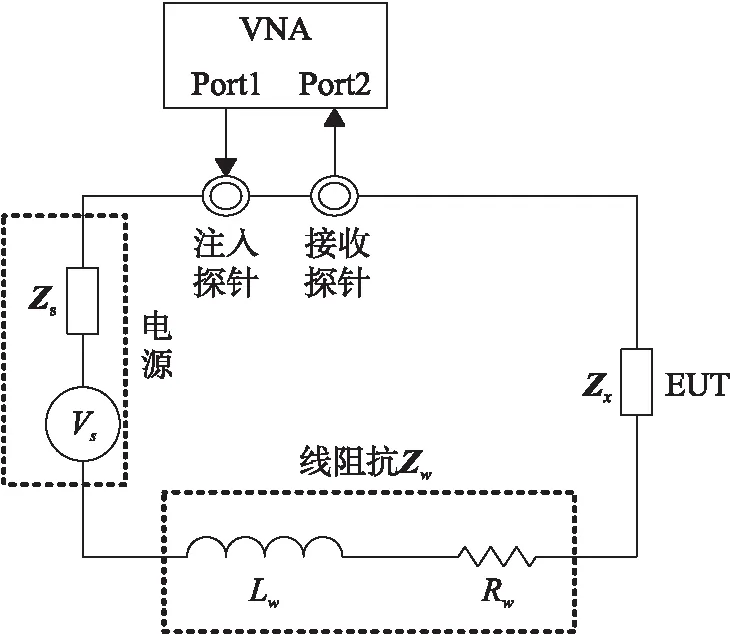
圖1 EMI噪聲源阻抗提取原理Fig.1 EMI noise source impedance extraction principle

如圖1所示,射頻信號從端口1輸入并在端口2被接收. 測試系統由DC/AC電源VS供電,其中ZS是電源阻抗,ZX是EUT的阻抗,ZW是連接電路線路的等效串聯電阻和電感阻抗.

根據散射參數法,VP1=(1+S11)·V1,VP2=S21·V1. 用ZX表示的測量阻抗可以描述為:

(4)

K和Zsetup分別表示測量回路的比率常數和阻抗. 如圖1所示,需要進行三次測量,得到三組散射參數.

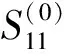
(5)

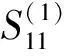
(6)

第3次測量時連接ZX,其中反射系數和透射系數分別為S11和S21. 根據式(4)和(6),可以直接求得噪聲源阻抗ZX:

(7)

2 基于SP-DE算法的噪聲源阻抗等效RLC參數提取方法

根據式(7)可以獲得EUT的噪聲源阻抗ZX,但只能獲得ZX的幅值和相位. 為了提高SP法的精度,提出了一種基于SP-DE算法的噪聲源阻抗提取方法,確定噪聲源阻抗的等效RLC參數,以改進EMI濾波器的設計.

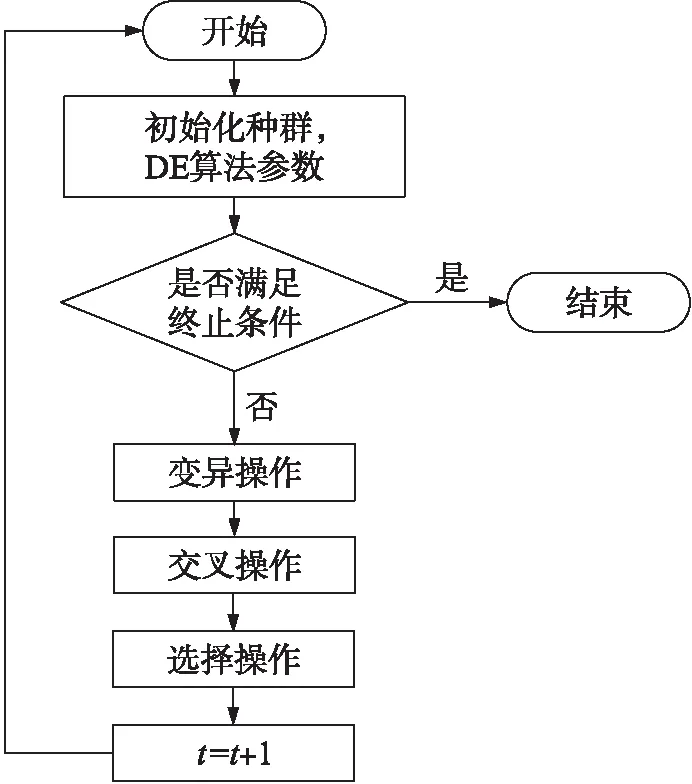
圖2 DE算法流程圖Fig.2 DE algorithm flow chart

2.1 DE算法原理

DE算法是一種并行直接搜索算法,它從隨機選取的初始種群開始對候選種群進行隨機操作,其主要操作過程包括選擇、交叉和變異. DE算法的流程圖如圖2所示.

2.2 DE算法的實現步驟

本文利用DE算法提取噪聲源阻抗的等效參數,具體實現步驟如下:

第1步,提出噪聲源的等效電路拓撲,獲得其阻抗Z的表達式. 噪聲源的等效電路拓撲可以根據器件的相關原理和功能進行設計,再通過DE算法建模,然后根據獲得的模型的仿真與測量對比進行驗證和再優化.

第2步,提取噪聲源阻抗信息. 基于DE算法的等效電路建模,需要根據相應噪聲源的阻抗信息求解由其等效電路模型所推導出的關于阻抗Z的表達式以獲取其最優的等效模型RLC參數.

第3步,最優參數問題轉化. 將由噪聲源的等效電路拓撲獲得的阻抗Z的表達式轉化為其阻抗幅值ZX的表達式,然后將ZX作為待優化RLC參數的原始函數,測量獲得的阻抗數據Zm為樣本. 設等效電路模型阻抗幅值ZX的表達式為:

(8)

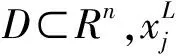
(9)

式中,φ(f)為測量獲得的阻抗幅值,φ(f)′是噪聲源阻抗等效電路的阻抗幅值計算值. 當變量Q為最小值時,對應的RLC參數即為最優參數.

(10)

式中,NP為種群大小,xi(0)指總體中第0代的第i個個體,xj,i(0)指第0代的第i個個體的第j個基因. rand(0,1)表示0到1之間的隨機分布數.

第5步,變異操作. DE以實際值參數向量作為每一代的種群,以種群中兩個個體的加權差值作為中間個體,即差向量. 然后將差向量加到第3個個體上,產生突變,如下所示:

vi(g+1)=xr1(g)+F(xr2(g)-xr3(g)).

(11)

式中,F是誘變因子,xi(g)是g代種群的第i個個體.

第6步,交叉操作. 交叉操作是指按照一定的規則將當前種群中個體的某些組成部分與突變個體的相應組成部分進行交換,從而產生交叉種群.g代種群|xi(g)|及其變異量{vi(g+1)}的交叉運算如下:

(12)

式中,vj,i(g+1)為變異量vi(g+1)的第j個基因,jrand是[1,2,3….D]中的隨機整數,CR是交叉概率.

第7步,操作選擇. 如果下一代個體的目標函數小于當前個體的目標函數,則下一代個體將取代當前個體.

(13)

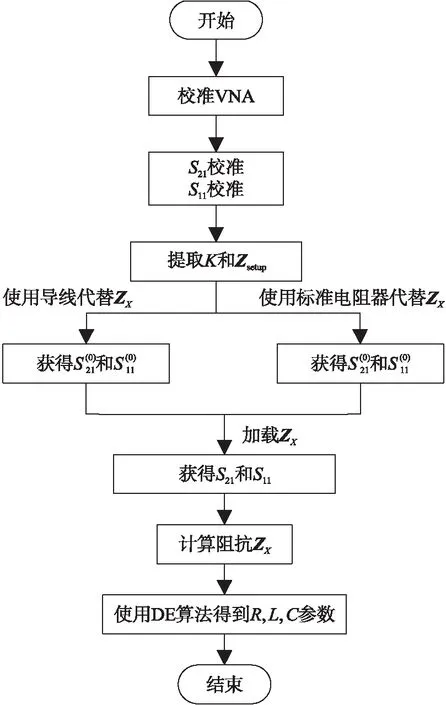
圖3 SP-DE法實現流程Fig.3 Implementation process of SP-DE method

第8步,收斂判別操作. 設x(g+1)中的最優個體為xbest(g+1),當DE運行到預定次數或目標函數值Q達到設定的精度時,操作即可結束,預估結果為RLC參數的最優值. 如果沒有收斂,則返回第二步,再次進行變異、交叉和選擇.

3 實驗驗證及分析

為驗證該方法的有效性,本節將一款LISN作為受試設備,采用SP-DE法對其進行內阻抗建模并與GB/T6113.102—2008標準中的理論值進行比較.

以一款LISN(型號:ROHDE&SCHWARZ ESH3-Z5 9 kHz～30 MHz)作為噪聲源,首先用SP法提取其阻抗信息. SP法實施時采用設備如下:電流探頭(型號:ZN23101 0.01 MHz～60 MHz),分別用作注入探頭和檢測探頭、VNA(型號:ROHDE&SCHWARZ ZNC3網絡分析儀9 kHz～3 GHz)用于注入和接收電壓信號. 然后用DE算法對提取的阻抗信息進行處理以獲取噪聲源阻抗的等效RLC參數. 具體流程如圖3所示.

被測LISN的實物如圖4(a)所示,根據其內阻抗測得曲線設其等效電路拓撲如圖4(b)所示.

圖4 LISN及其等效電路Fig.4 LISN and its equivalent circuit

由圖4(b)的等效拓撲模型,可得出LISN內阻抗等效電路的阻抗表達式如下:

(14)

式中,ZLISN為LISN的內阻抗,R、L、C為LISN內阻抗等效模型中對應的電阻、電容、電感等效參數,ω=2πf,f為頻率.

LISN的內阻抗提取實驗布置如圖5所示. 實測采樣點個數為301個,測試頻率為9 kHz～30 MHz. 然后通過DE算法處理測得阻抗數據,尋找LISN內阻抗等效電路模型的最優RLC參數.

基于SP-DE法的該LISN內阻抗的等效R、L、C參數如表1所示,其內阻抗等效模型精度與實際測量值對比如圖6所示.

圖5 LISN阻抗提取實驗布置Fig.5 LISN impedance extraction experiment layout

表1 LISN內阻抗等效模型參數值Table 1 Parameter values of LISN internal impedance equivalent model

由圖6可知,LISN內阻抗等效電路模型雖與標準值仍存在一定的誤差,但誤差很小,阻抗實部、虛部以及阻抗幅值的誤差均在3 Ω以內,在9 kHz～30 MHz 頻段內與實際測量值基本吻合,因此本文提出的SP-DE法可以較為準確的實現被測設備的內阻抗建模.

圖6 基于SP-DE法的LISN內阻抗模型與測量值對比Fig.6 Comparison of internal impedance model and measured value of LISN based on SP-DE method

4 基于SP-DE法的濾波器設計與應用

為了驗證該方法的實用性,此次采用開關電源作為EUT進行傳導EMI噪聲抑制實驗. 用SP-DE法提取開關電源的內阻抗,并根據阻抗數據設計濾波器以抑制傳導EMI噪聲.

4.1 濾波器設計

采用SP-DE法設計濾波器:以SP法提取的ZX為基礎,利用DE算法對ZX進行擬合優化,得到開關電源內阻抗的等效RLC參數,然后根據這些參數設計濾波器. 開關電源EMI濾波器拓撲如圖7(a)所示,實物如圖7(b)所示.

圖7 開關電源EMI濾波器拓撲及實物Fig.7 Switching power supply EMI filter topology and physical

圖8 傳導EMI測試布局Fig.8 Conducted EMI test layout

4.2 抑制分析

本次測試基于標準EN55022,測試設備包括:人工電源網絡(AMN,Model:ROHDE &SCHWARZ ENV216 TWO-LINE V-NETWORK 9 kHz～30 MHz)和EMI接收機(Model:ROHDE&SCHWARZ ESL EMI TEST RECEIVER 9 kHz～3 GHz). 測試布局如圖8所示,開關電源的輸入為220±20% VAC,輸出為12 V/3 A,負載為800 Ω純阻性負載.

該開關電源傳導EMI初始測試結果如圖9(a)所示,實線為傳導EMI峰值測試結果,虛線為傳導EMI平均值測試結果. 測試頻段為150 kHz至30 MHz,帶寬為 9 kHz. 該濾波器在1 MHz頻率下的特性為:差模電感L1=1.33 mH,共模電感L2=31.08 mH,電容C1、C2均為0.58 μF,其抑制效果如圖9(b)所示,該濾波器總體上抑制效果良好,尤其是在10 MHz以下的頻段有比較明顯的抑制效果,噪聲抑制最大處接近35 dBμv.

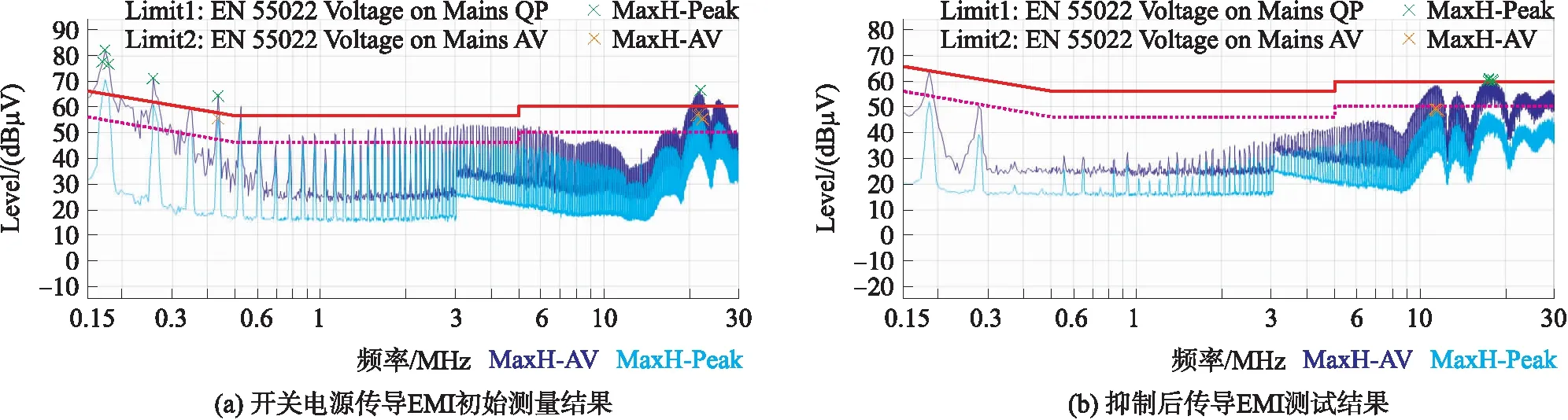
圖9 抑制前后對比Fig.9 Comparison before and after suppression

5 結論

針對傳統內阻抗建模方法存在的缺陷,本文提出了一種基于SP-DE法的噪聲源內阻抗建模方法. 首先基于SP法推導了噪聲源內阻抗的一般表達式,它涵蓋了所有頻點的阻抗特征,為進一步分析噪聲源阻抗奠定了基礎. 然后采用DE算法處理SP法提取的噪聲源內阻抗信息,以獲得噪聲源內阻抗等效RLC參數,實現對噪聲源內阻抗的建模,該算法控制變量簡單,通用性強. 最后基于本文提出的方法進行了濾波器設計與傳導EMI噪聲抑制實驗. 實驗結果表明,基于SP-DE法設計的濾波器具有較好的傳導EMI噪聲的抑制效果,驗證了該方法實現的內阻抗建模具有良好的精確度.