近海廢棄物收集系統壓縮裝置運動學與動力學分析＊

青島科技大學機電工程學院 青島 266061

0 引言

近年來，海洋廢棄物影響海洋景觀，威脅航行安全，對海洋生態系統產生巨大影響。因此，為了更好地保護海洋環境，設計研究出能夠回收海洋廢棄物的相關裝備具有重要意義。一些科研機構及公司著手研究水面漂浮垃圾收集裝置[1-4]；上海工程技術大學的研究人員提出一種針對水面垃圾清理船的動力推進裝置，并對裝置進行軌跡分析[5]；吉林大學張玉新等設計水面垃圾清理船，對負責清理工作的執行機構進行仿真研究工作，利用ADAMS 確定裝置關鍵參數，并驗證結構的合理性[6]；陳蘇、王中壢等針對水面垃圾清理裝置的智能化控制和自動化駕駛等方面進行研究[7，8]；上海水產大學工程學院的陳金穩、張麗珍等針對船用明輪的結構進行設計，對明輪的參數做出優化，提高結構效率，提升整機的工作性能[9]；Andrew J 設計多種方法相融合的收集裝置[10]；Choi Gi Eok 研究收集物的粉碎裝置，通過機械式結構，實現收集物的高效粉碎[11]。

目前，國內外針對近海廢棄物收集系統的裝置研究有很多，不同的裝置能實現不同的功能，但對收集系統中的壓縮裝置研究較少[12]。在收集過程中缺乏對廢棄物的有效壓縮會使收集后的廢棄物存在大量水分，且廢棄物較為蓬松，無法實現大量的收集，更無法實現收集系統集打撈、運輸、脫水、壓縮的一體化功能。為此，本文重點研究收集系統的壓縮裝置，使收集的廢棄物能夠完成脫水、壓縮過程，進而有效增加系統的收集容量，提高收集效率，為后期的運輸提供便利。

1 壓縮裝置的結構組成

如圖1 所示，近海廢棄物收集系統中壓縮裝置主要由液壓缸、推板、滑軌、壓縮艙體、進料斗等部件組成。

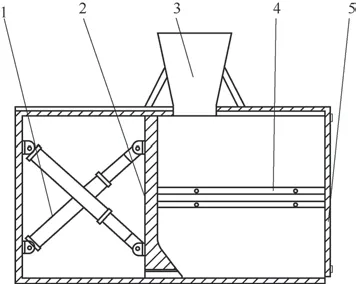
圖1 壓縮裝置結構示意圖

2 運動學分析與數值計算

2.1 運動學分析

對壓縮裝置的執行部分進行運動學分析，研究執行桿件在運動過程中角度的變化與推板位移、速度等參數之間的關系，壓縮裝置運動簡圖如圖2 所示。

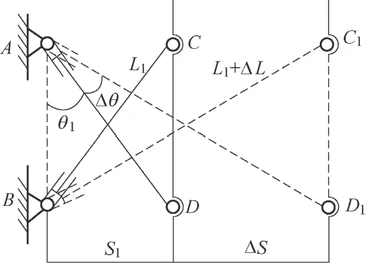
圖2 壓縮裝置運動簡圖

在圖2 中，AD1＝BC1，壓縮裝置在初始工作位置時，液壓缸與底座連線夾角為θ1，初始壓桿長度為L1，推頭與液壓缸底座間距為S1。當壓縮裝置完成壓縮后，最終壓桿長度為L1+△L，壓桿長度伸長量為△L，推頭與液壓缸底座間距增加△S。在△ABD1中可得

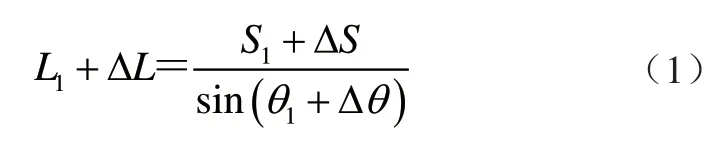
由三角形正弦定理可得

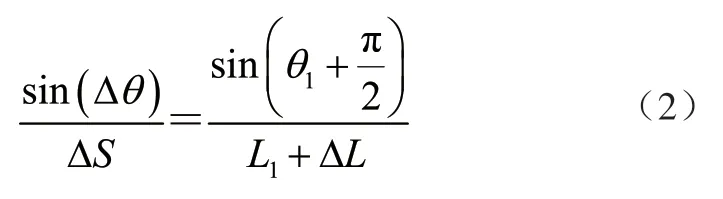
將式（1）、式（2）整合，得到推頭的位移△S 與液壓缸旋轉角△θ 之間的關系為

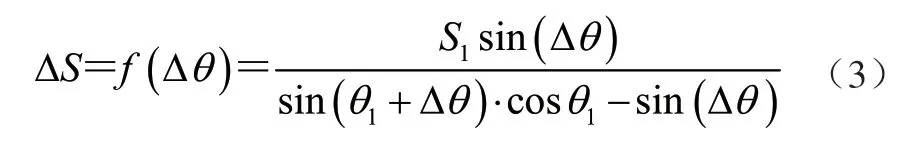
在式（3）中，如果θ1和S1為固定值，△S 與△θ成正比關系。隨著液壓缸旋轉角度的增大，△S 不斷增加，當△θ 達到最大值，液壓缸的推桿伸長量達到最大，推頭到達極限工作位置。

△ADD1三角函數公式對時間取一次導數，可得其推頭的移動速度和液壓缸的轉動速度之間的表達式為

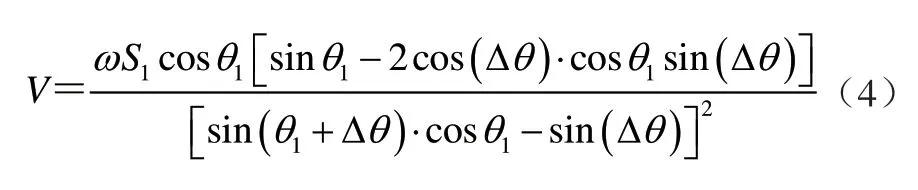
2.2 數值計算

根據壓縮裝置的運動學分析，使用Matlab 軟件分別對推頭的位移△S 與液壓缸旋轉角△θ 之間的函數關系和推頭移動速度與液壓缸速度之間的函數關系做數值計算。由于設計的壓縮推頭與液壓缸底座間距S1為928 mm，推壓液壓缸與底座連線的初始夾角θ1為47°，將S1和θ1作為已知量帶入關系式，得到推頭位移與液壓缸旋轉角關系曲線如圖3 所示；將液壓缸速度的變化范圍與時間變化范圍代入關系式，得到推頭移動速度和液壓缸速度變化曲線如圖4 所示。

由圖3 可以看出，隨著液壓缸旋轉角度△θ 的增大，推頭的位移△S 也在逐漸變大，變化趨勢與預期相符。當旋轉角達到最大變化角度，對應的△S 數值為846 mm。由圖4 可以看出，在0～3 s 內，液壓缸的速度逐漸增大，推板的速度也逐漸增大；當t ＝3 s 時，推頭的移動速度為102 mm/s。

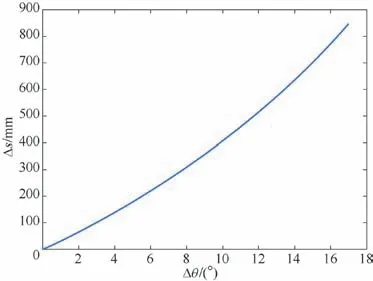
圖3 推頭位移與液壓缸旋轉角關系曲線

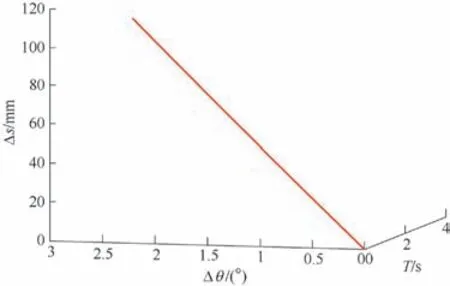
圖4 推頭移動速度和液壓缸速度變化曲線

3 壓縮裝置的動力學仿真

壓縮裝置是整個廢棄物收集裝置的關鍵機構。在壓縮過程中，需要通過推板滑軌實現壓縮裝置的往復運動，同時液壓缸對壓縮裝置提供動力源。壓縮機構設計的合理性關系到整個壓縮裝置的使用性能和工作效率，因此有必要研究壓縮裝置在工作過程中的平穩性，保證機構的設計合理可靠。本文對壓縮裝置做動力學仿真分析，動力學仿真分析流程如圖5 所示。

3.1 仿真設置

在動力學仿真過程中，鑒于ADAMS 仿真軟件在建模能力的局限性，選擇Solidworks 三維軟件完成對壓縮裝置的三維建模。考慮實際工況下的要求，對模型完成混合屬性相關參數的設置，在重力設置中選擇真實重力存在狀態，使虛擬模型更加符合真實情況。在合理的添加約束和運動副、驅動與載荷的同時，簡化操作過程，對模型完成動力學仿真分析。

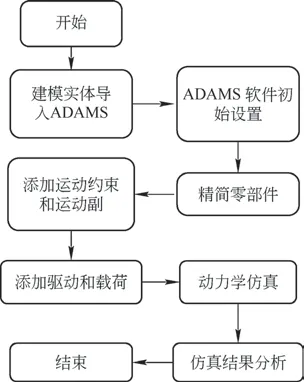
圖5 動力學仿真分析流程

1）添加約束和運動副

壓縮裝置的執行機構缸筒端安裝在側板，側板與船體固定，無相對運動；執行機構的液壓缸桿端安裝在推板，與推板間有相對運動。其中，液壓缸筒與側板間所構成的運動副及液壓缸桿與推板間構成的運動副定義為轉動副。推板和底板間、液壓杠桿與液壓缸筒間構成的運動副定義為移動副，艙體周圍各板定義為固定約束。

2）添加驅動與外部載荷

液壓缸的驅動函數選擇階躍函數，壓縮推板的外部載荷函數選擇Step 函數。階躍函數的表達式為

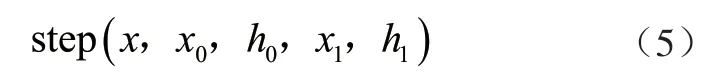
式中：x 為自變量，通常為時間的任一函數；x0為自變量的階躍函數初始值；h0為階躍函數的初始值；x1為自變量的階躍函數結束值；h1為階躍函數的結束值。

3.2 結果與分析

1）推板動力學仿真

推板在X 方向的位移曲線如圖6 所示。由圖6 可知，推板的初始位置為1 120 mm，第10 s 達到最大位移1 948 mm。在0～10 s 期間，推板從初始位移的1 120 mm 變化到最大位移1 948 mm，△S 數值為828 mm；在第10 s 處液壓缸的推桿伸長量達到最大時，推頭也到達極限工作位置；在10～13 s 期間，推板進入保壓狀態，位移保持不變，大小仍為1 948 mm；在13～20 s 期間，液壓缸驅動推板返回初始位置。

壓縮推板在Y、Z 方向的位移曲線如圖7 所示。由圖7 可知，推板在工作周期內，其Y、Z 方向位移始終保持不變，裝置在Y、Z 方向未發生跑偏，保證了壓縮質量。綜合推板在X、Y、Z 方向的位移曲線可以看出推板在周期內做直線運動，運動方向沿X 方向，在Y、Z 方向沒有大幅度的跳動，總體比較平穩。

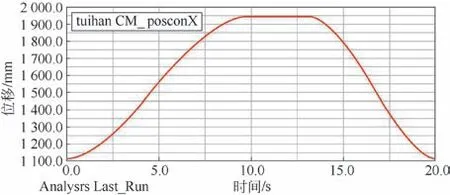
圖6 推板X 方向位移曲線

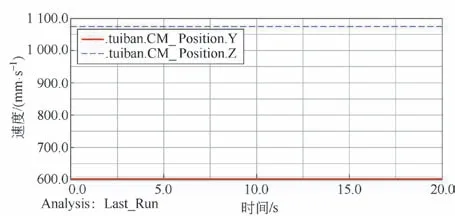
圖7 推板Y、Z 方向位移曲線

推板在X 方向和Y 方向的速度曲線如圖8 和9 所示。由圖8 可知，推板在0～10 s 期間速度先增加后降低，在第4.7 s 達到正向最大速度123.19 mm/s；在10～13 s 期間裝置處于保壓階段，速度大小保持不變；在13～20 s 期間速度先增加后降低，在16.8 s 達到最大反向速度176.21 mm/s。

由圖9 可知，推板在Y 方向上的最大速度為1.94×10-10mm/s，其數值可以忽略。因此，在工作過程中，推板在縱向比較穩定，波動較小。

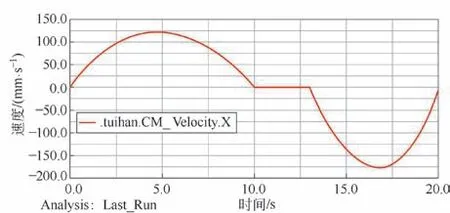
圖8 推板X 方向速度曲線

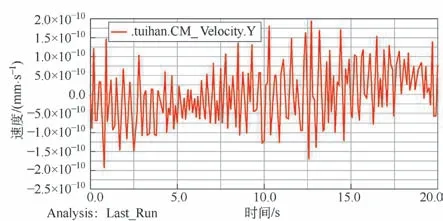
圖9 推板Y 方向速度曲線

由于推板在Y 方向速度變化數值很小，故無需分析推板在Y 方向的加速度曲線，推板在X 方向的加速度曲線如圖10 所示。由圖10 可知，推板的加速度處于緩慢波動，但在第10 s 和第13 s 處的加速度變化較大，對壓縮裝置會產生較大沖擊，影響液壓缸的工作壽命。

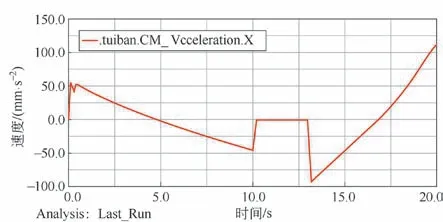
圖10 推板在X 方向加速度曲線

2）液壓缸動力學仿真

由于壓縮裝置中的液壓缸均為對稱分布，故在此僅對中部液壓缸的運動參數進行分析，前后液壓缸的運動參數與之對應。其中，關于液壓缸的轉動速度曲線如圖11 所示。

由圖11 可知，液壓缸的速度在0～10 s 期間先增加后降低，在3 s 處達到最大速度，數值為2.78 deg/s；在10～13 s 期間系統處于保壓階段，速度為0；在13～20 s 期間裝置處于回程階段，此時液壓缸的速度相對進程數值來說是增大的，在18.1 s 時達到3.94 deg/s,總體來看液壓缸的速度變化相對平穩。

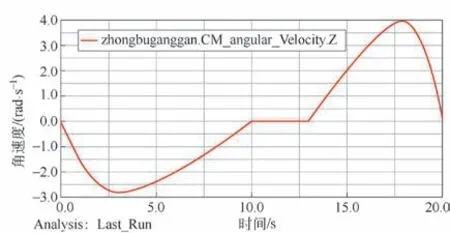
圖11 液壓缸轉動速度曲線

由圖11 可知，當3 s 時，在液壓缸轉動速度為2.78 deg/s ；由圖4推頭移動速度和液壓缸速度變化曲線可知，在3 s 時推頭移動速度為102 mm/s；由圖8 推板在X 方向的移動速度曲線可知，其在3 s 時速度為108 mm/s，這一結果與Matlab 數值計算結果比較吻合，相對誤差為5.9 %。液壓缸的加速度曲線如圖12 所示。

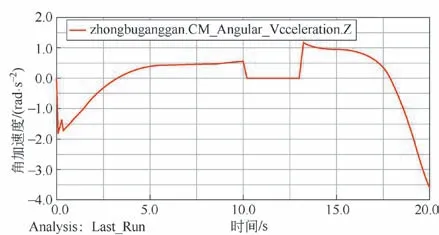
圖12 液壓缸加速度曲線

由圖12 液壓缸加速度曲線對比于圖11 液壓缸轉動速度曲線可知，在0～3.2 s 期間，加速度方向與速度方向保持一致，對應速度逐漸增加，增加趨勢變緩；在3.3～10 s 期間，加速度始終大于0，逐漸增加，對應速度逐漸降低；在13～17.8 s 期間，加速度平穩降低，對應速度逐漸增加；在17.9～20 s，加速度反向增加，速度逐漸降低。在壓縮裝置運動的啟停點，其加速度發生較大變化，由此可判斷在裝置的啟停和保壓啟停階段，裝置的穩定性較低。

從液壓缸和鉸接點的受力情況進行分析，取上部鉸接點受力曲線如圖13 所示，液壓缸受力如圖14 所示。

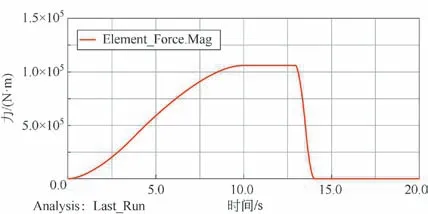
圖13 液壓缸上鉸接點受力曲線

由圖13 可知，鉸接點處的受力曲線隨壓縮裝置的工作過程先緩慢增加后保持不變，在10.2 s 處達到最大數值為106 460 N。保壓完成后，在13 s 處裝置開始回程，鉸接點處受力急劇降低。

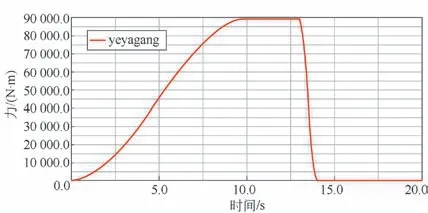
圖14 液壓缸受力曲線

由圖14 可知，液壓缸在初始階段的受力逐漸增加，第10.2 s 處受力達到最大，數值為89 487 N；在10.2～13 s 期間裝置處于保壓階段，受力保持不變；在13 s 處裝置回程，受力逐漸降低，整體受力平穩，無劇烈增減情況，對裝置整體沖擊不大。綜合圖13 和14 可知，液壓缸的受力曲線變化與鉸接點處的受力曲線變化趨勢相同，雖在行程和回程的交界點處存在沖擊力，但總體對液壓缸的影響不大，仿真數據與實際相符。

液壓缸的角度變化曲線如圖15 所示。由圖15 可知，液壓缸的初始角度θ1數值為47°；在行程中，角度逐漸增加，第10 s 達到最大角度63.8°；保壓完成后，角度逐漸降低，最終在20 s 時刻點達到初始角度47°。由圖15 還可以看出，在△θ 的變化區間內，推板從初始位移的1 120 mm 變化到最大位移1 948 mm，△S 數值為828 mm。這一結果與Matlab 數值計算結果846 mm 比較吻合，相對誤差為2.2%。

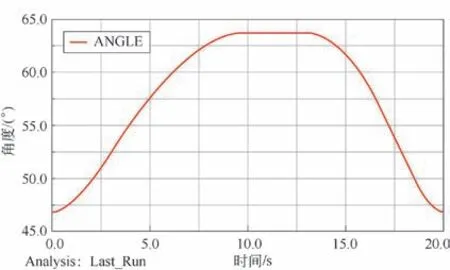
圖15 液壓缸角度變化曲線

4 結論

1）數值計算結果表明，推頭位移隨液壓缸旋轉角度的增大而逐漸增大，推板的移動速度隨液壓缸速度的增加而逐漸增加，基本保持線性相關。

2）仿真分析結果表明，推板沿X 方向做直線運動，在沿X 方向的運動過程中會對壓縮裝置產生沖擊力，在Y、Z 方向上無大幅度跳動，比較平穩；整個壓縮裝置在啟停、保壓啟停階段的穩定性較低，但總體來說裝置在啟停階段產生的沖擊力對液壓缸的影響不大。

3）動力學仿真分析結果與Matlab 數值計算結果比較吻合，推頭移動速度的相對誤差為5.9%。推頭位移的相對誤差為2.2%。