角解型內生Tobit模型交互效應和平方效應的估計與推斷*
——對家庭風險資產配置比例模型的應用

周先波，李赫揚

一、引 言

微觀數據建模中的因變量常具有歸并數據特征，如病人住院時間長短、家庭風險資產配置比例、企業研發投入、老年人勞動時間供給等。造成這種歸并的原因常有兩種：一種是研究者（數據收集者）對因變量數據不能完全收集；二是研究對象個體的最優選擇落于選擇空間的邊界上（即角解）。為簡單起見，設因變量數據歸并點或角解為0，則刻畫歸并因變量的模型為Tobit 模型：y= max{x′β+ε，0}。上述兩種原因的區別在于，前者研究的是解釋變量對潛變量y*=x′β+ε的邊際影響，即β的估計；后者研究的是解釋變量對受限因變量期望水平的邊際影響，即E[y|x]偏導函數的估計。可見，兩種原因對應的研究目的存在較大的差異。事實上，研究個體經濟行為的問題常由第二種歸并原因引起。例如，家庭對風險資產配置的選擇可能為零，在邊界上達到家庭消費效用最大化；企業對研究開發的投入可能為零，在邊界上的選擇使企業利潤最大化；老年人勞動時間的供給可能為零，不參加勞動使老年人的效用最大化，等等。

在實證中，研究者常通過引入解釋變量的平方項、交互項，以反映解釋變量的非線性效應和調節效應。在上述第一種原因情形下，平方項、交互項的系數可以反映解釋變量影響因變量的平方效應和交互效應，但在第二種原因情形下，角解型Tobit 模型平方效應、交互效應并非如此簡單，正確做法涉及到E[y|x]關于平方項和交乘項中解釋變量的二階偏導函數的估計。Ai and Norton（2003）給出外生解釋變量情形下非線性模型中交互效應估計與檢驗的正確做法。此方法在實證中被廣泛應用，如Karaca-Mandic et al.（2012），Haywood（2016），Mulkay（2019），Meoli et al.（2020）等。國內學者也逐漸重視應用Ai and Norton（2003）方法估計Probit 和Logit 模型中的交互效應或平方效應。例如，嚴兵和張禹（2016）、鄧慧慧和虞義華（2018）、夏后學等（2019）、周先波和歐陽夢倩（2019）等對交互效應或平方效應進行了正確的估計與分析。

不過，Ai and Norton（2003）方法及相應的實證研究只適用于外生解釋變量情形。解釋變量的內生性相當重要，是研究者在實證分析中經常碰到的問題（如見：方穎和趙揚，2011；李兵和任遠，2015；薛景等，2019）。對于含內生解釋變量的歸并因變量模型，在上述第一種原因情形下，由IV-Tobit 估計，平方項、交互項的系數可以解釋自變量影響因變量的平方效應和交互效應。但在上述第二種原因情形下，這種做法失效。此時，簡單地以IV-Tobit估計中平方項、交互項的系數及其顯著性來解釋自變量影響因變量的平方效應和交互效應，或者應用外生解釋變量情形下Ai-Norton方法所估計的交互效應來解釋內生自變量影響受限因變量的交互效應，均是不合適的。目前文獻沒有給出內生解釋變量情形下角解型Tobit模型中交互效應和平方效應的估計方法。鑒于此，本文著眼于研究此類角解型內生Tobit模型中自變量的邊際影響、平方效應和交互效應的估計與檢驗方法，并給出應用實例。本文研究的貢獻是將只適合于外生解釋變量情形下非線性模型中交互效應的Ai-Norton估計方法推廣至適合于內生解釋變量情形。

本文其余部分安排如下：第二部分給出內生角解型Tobit 模型中邊際效應、平方效應和交互效應的估計與檢驗方法；第三部分設計數值模擬，說明我們方法的良好有限樣本表現，以及忽視角解性質與內生性的方法在估計真實效應時的較大偏誤；第四部分應用本文方法，實證研究家庭新型信息化工具使用和家庭對外關系變量對家庭風險資產配置比例的邊際影響、交互效應以及年齡的平方效應；最后是總結。

二、邊際影響、交互效應和平方效應的估計與檢驗

因為平方效應是交互效應的特例（交乘的兩個解釋變量是相同的），我們重點討論模型中含交互項時邊際影響和交互效應的估計和檢驗。考察角解型Tobit模型（corner-solution Tobit model）：

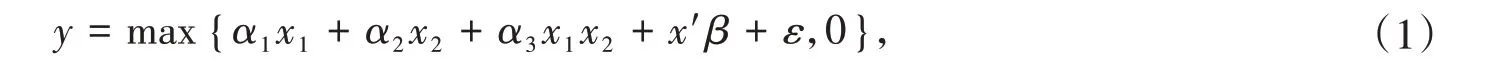
其中y是被解釋變量，其歸并特征是由個體的最優選擇發生于邊界所造成；x1，x2為我們關注的兩個解釋變量，x1x2是它們的交互項，x1和x2均可能具有內生性（即與擾動項ε相關）。其他解釋變量向量為x，均是外生的。因為y可能是角解（在邊界上取零），故x1，x2影響y的邊際效應和交互效應不是它們的系數α1，α2，α3，而應通過y的條件期望來計算和估計。

（一）Ai-Norton方法：解釋變量均為外生

先簡述解釋變量均為外生情形下交互效應的Ai-Norton 估計方法。設x1和x2均與ε相互獨立，且ε～N(0，σ2)，經計算知，y的條件期望函數是：

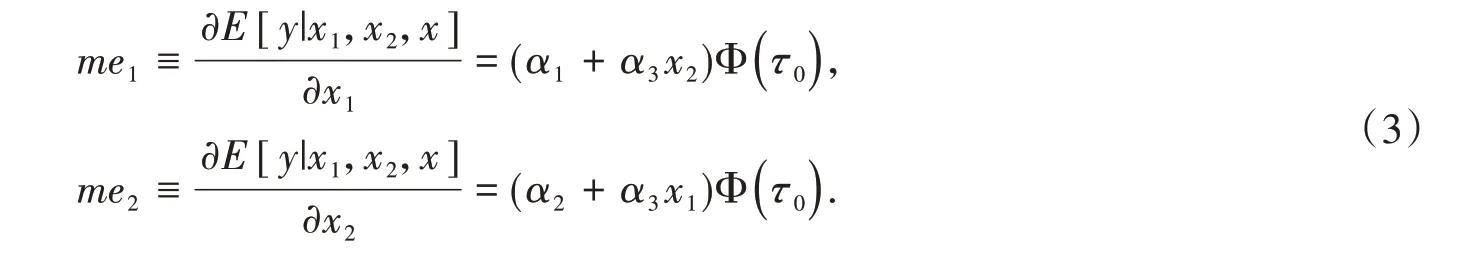
由此，x1，x2的交互效應是：

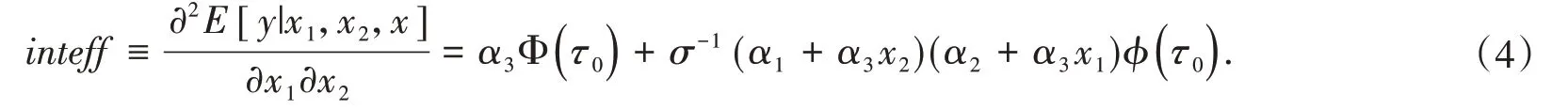
可見，由交互項系數α3的估計，或者交互項x1x2對y回歸函數邊際影響α3Φ(τ0)的估計作為x1，x2影響y交互效應的估計是不恰當的。

（二）本文方法：x1和x2為內生解釋變量

當x1和x2均是內生的連續解釋變量時①對于x1和x2只有一個變量是內生的情形，下文簡化式方程只有一個，討論是類似的。下文模擬也考慮了這種情形；實證應用也是這種情形。，Ai-Norton 方法不能用于估計角解型內生Tobit 模型中的邊際影響和交互效應。本節給出一種合適的估計方法，它依賴于控制函數（control function）方法（Newey，1987；Rivers and Vuong，1988）的應用。記內生變量x1和x2的工具變量構成的列向量為z，設簡化式模型為：

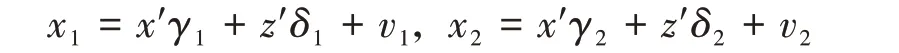
其中(ε，v1，v2)服從均值為零向量的聯合正態分布，且獨立于x，z。記ε=θ1v1+θ2v2+e，其中e服從正態分布且條件獨立于變量x1，x2，x1x2，x，v1，v2。將ε=θ1v1+θ2v2+e代入模型（1），得

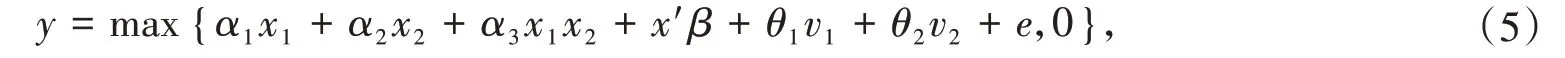
記在給定的條件下，y 的條件期望是E[y|x1，x2，x，v1，v2]=σe[τΦ(τ)+φ(τ)]，其 中現v1，v2可由簡化式模型估計的殘差得到估計，故我們可由以下兩階段方法估計y的條件期望函數E[y|x1，x2，x]。

第一階段：分別將x1和x2關于x，z進行OLS回歸，得到殘差

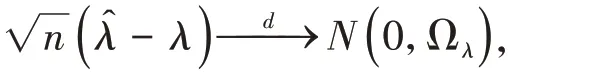
其中Ωλ是估計量的漸近方差。給定x1，x2，x，由Wooldridge（2010），條件期望E[y|x1，x2，x]可由一致地估計，其中記

則條件期望E[y|x1，x2，x]的邊際影響的估計分別為：

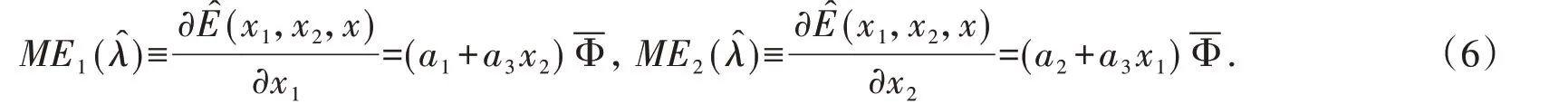
對（6）第一式關于x2或對（6）第二式關于x1求偏導可得，x1，x2交互效應的估計為：

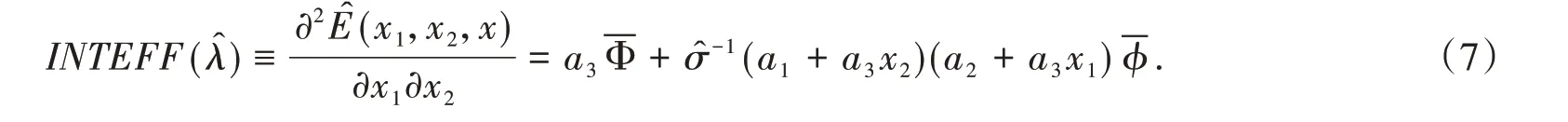
為了檢驗它們的顯著性，我們利用Delta 方法，可得到原假設ME1= 0，ME2= 0 以及INTEFF= 0 的檢驗統計量分別為：

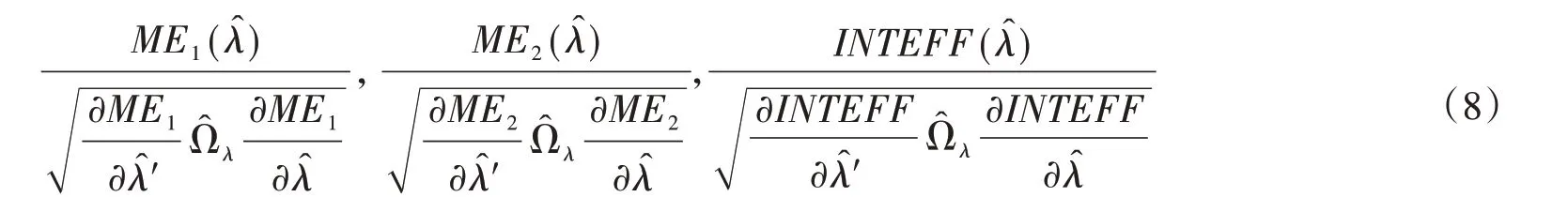
注1：除使用上述檢驗統計量（8）對原假設ME1= 0，ME2= 0 以及INTEFF= 0 進行檢驗外，還可以通過重抽樣bootstrap方法進行檢驗。下文實證中，我們由bootstrap方法檢驗。

注2：如果上述模型中含有某外生變量w及其平方項②如果w也具有內生性，我們可類似使用前述二步方法估計平方效應。因篇幅所限，此處從略。，則類似地可估計此變量的邊際影響和平方效應。將模型（5）中的x′β寫成β1w+β2w2+x′β，相應地，在上述兩階段估計中也這樣記號，則變量w對被解釋變量的邊際影響效應MEw和平方效應QEw的估計分別為：

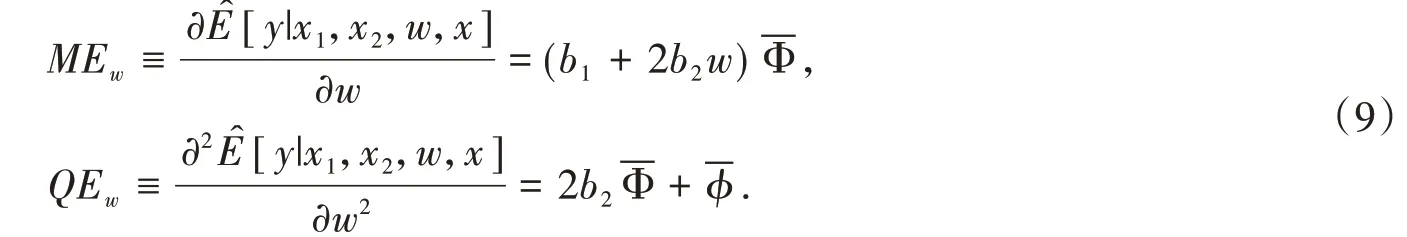
其中τi修改為在實證應用中，我們應用bootstrap方法檢驗MEw和QEw的統計顯著性。

三、數值模擬比較

本節構建Monte Carlo數值模擬，說明角解型內生Tobit模型的估計方法對交互效應的估計的有限樣本表現，并比較在忽視角解性和內生性時常用的估計方法的模擬表現，以之闡明不當方法對真實交互效應的估計具有較大的偏離。此模擬比較的目的是為了強調角解型內生Tobit 模型中交互效應正確估計的重要性③這里僅模擬交互效應，對邊際影響和平方效應等的模擬設計是類似的。因篇幅所限，不作贅述。。

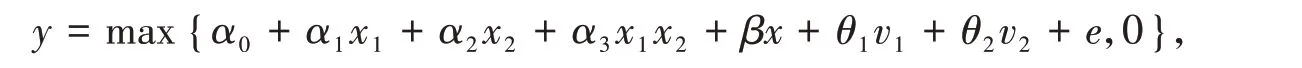
假設數據生成過程為：這 里α0= 0，α1= 1，α2= 2，α3= -1，β= 1，θ1= 1，θ2= -1，變 量x1= 1+x+ 3z1+v1，x2= 1+ 2x+2z2+v2，而x～N(-1，4)，e～N(0，1)，v1～N(0，1)，v2～N(0，2)，z1～N(0，4)，z2～N(0，3)獨 立地 生 成。最終記錄數據為

從可觀察數據來看，我們要估計的是以下模型：

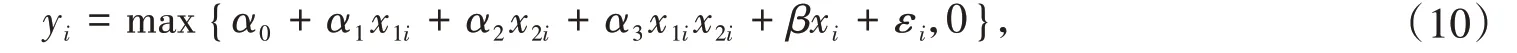
其中，εi≡θ1v1i+θ2v2i+ei與x1i，x2i相關，但與xi不相關，即解釋變量x1i和x2i在非線性歸并數據模型（10）中具有內生性，z1，z2是它們的工具變量。

由真正數據生成過程知，在x1，x2，x，v1，v2給定的條件下，x1，x2的真實交互效應是：

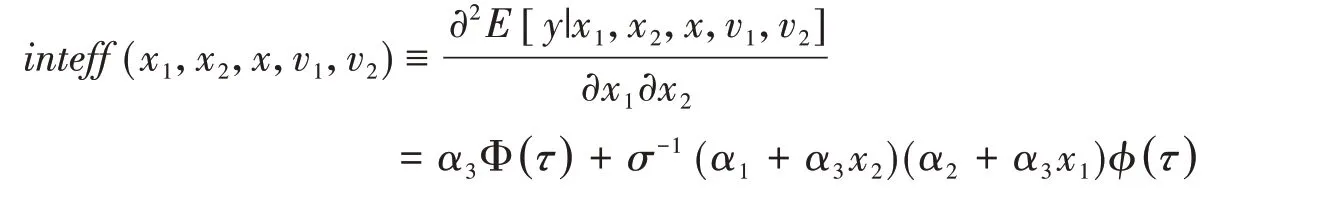
其中τ=τ(x1，x2，x) ≡α1x1+α2x2+α3x1x2+βx+θ1v1+θ2v2。所以，基于模型（11），在x1，x2，x給定的條件下，x1，x2的真正交互效應inteff(x1，x2，x)是：

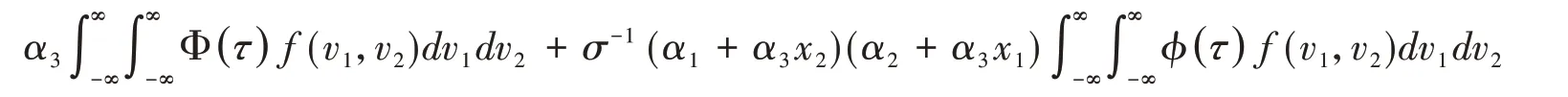
其中f(v1，v2)是v1，v2的聯合分布密度函數。按這里設定，因v1～N(0，1)和v2～N(0，2)相互獨立，故inteff可用下面逼近方法計算：由N(0，1)和N(0，2)獨立地生成M個點（這里取M=10000）計算inteff(x1，x2，x)為：

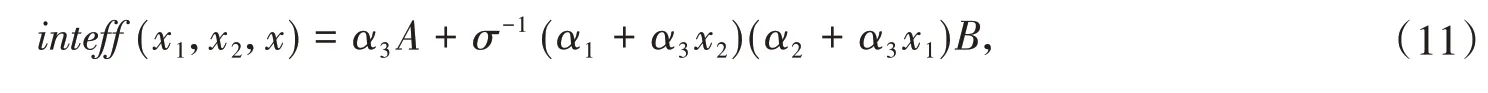
其中

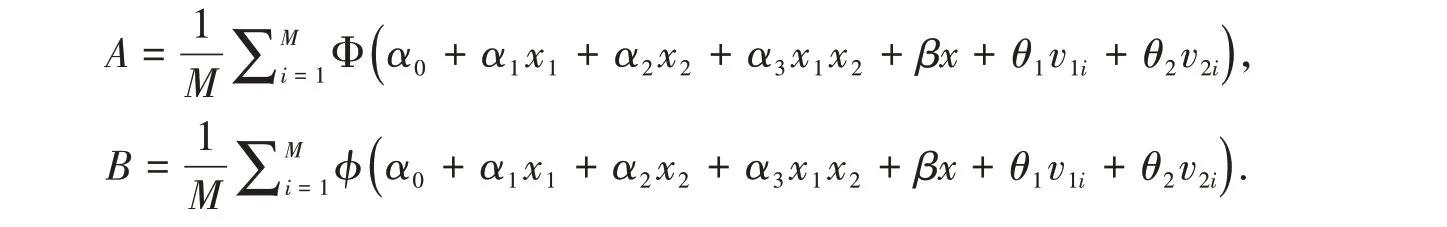
為比較起見，我們還報告沒有考慮內生性時交互效應的估計方法（即Ai and Norton 方法，2003），以及考慮內生性但僅用交互項的系數估計作為交互效應的估計的模擬結果。我們分別從模擬的偏誤、標準差和根均方誤等方面，考察上述三種方法的有限樣本表現及其與真實交互效應的差異程度。

因為交互效應為(x1，x2，x)的函數，我們只對它在(x1，- 1，1)點處值inteff(x1，- 1，1)進行模擬，其中x1取值-1，-0.5，0，0.5和1。表1報告五個點處交互效應的模擬結果，其中樣本容量分別是n=200和n=800。在我們內生模型設定下，Ai and Norton（2003）方法沒有考慮內生性，理論上應該不適合，從表1第一欄看，其有限樣本表現確實不佳；與本文方法相比，其表現要差得多，因為其偏誤、標準差和根均方誤都比較大。可見，由Ai-Norton方法估計角解型內生Tobit模型中的交互效應，在實際中是不合適的。

值得注意的是，在考慮到解釋變量的內生性，將控制變量第二階段估計中交互項的系數估計作為x1，x2交互效應的估計，也是不合適的。由表1的第二欄可見，相對于真實的交互效應，作為交互效應的估計量，其偏誤很大，有限樣本表現極差。這說明，實證應用中簡單地基于交互項系數估計作交互效應的分析和推斷具有方法論上的缺陷。

另外，由表1，在其他設定不變時，隨著樣本容量的增加，Ai-Norton方法對各點處交互效應的估計的偏誤并沒有呈減小的趨勢。同樣，交互項系數估計作為交互效應的估計量，偏誤很大的性質并沒有改變。而本文給出的交互效應估計相對于真實交互效應的偏誤和根均方誤均隨樣本量的增加相應減小。本文方法給出了內生Tobit模型中解釋變量交互效應的一個可靠估計。

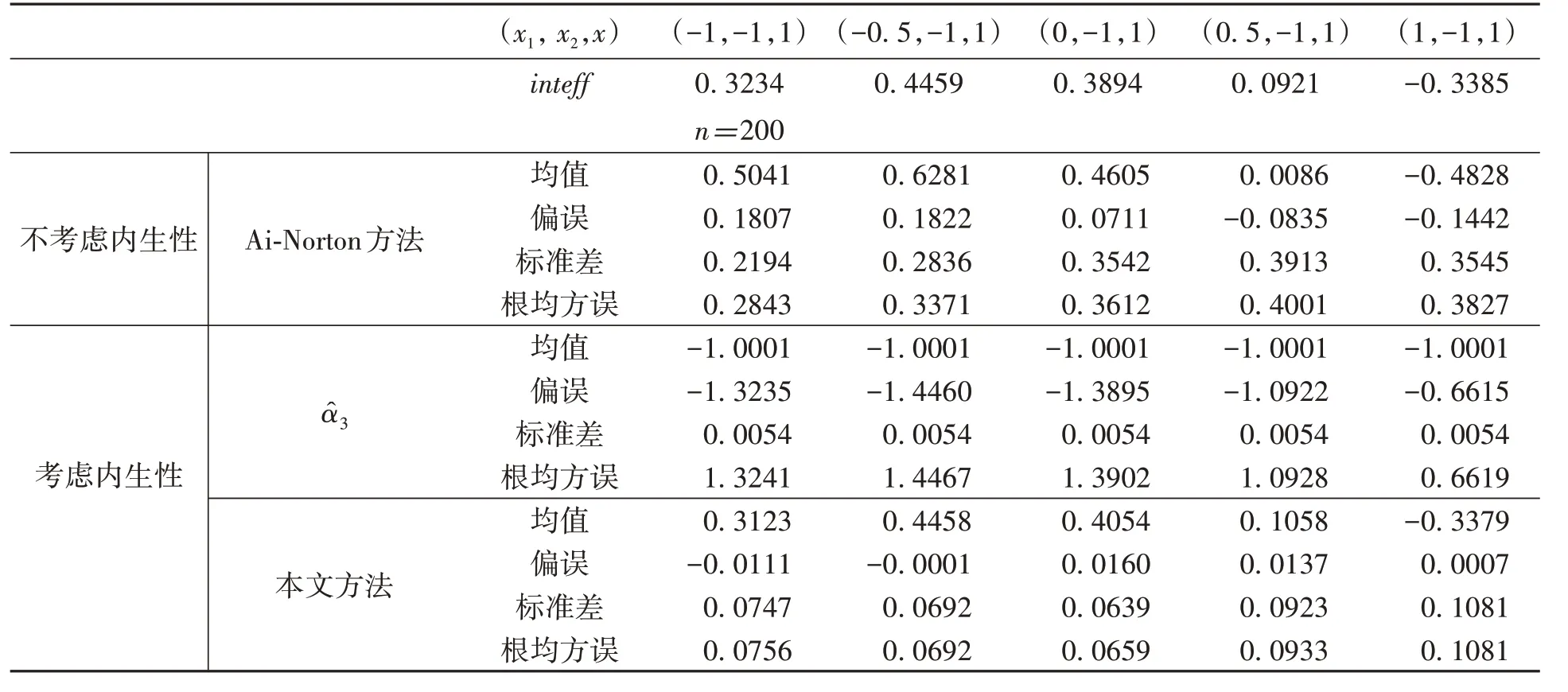
表1 交互效應inteff不同估計方法的模擬比較（x1，x2均內生）

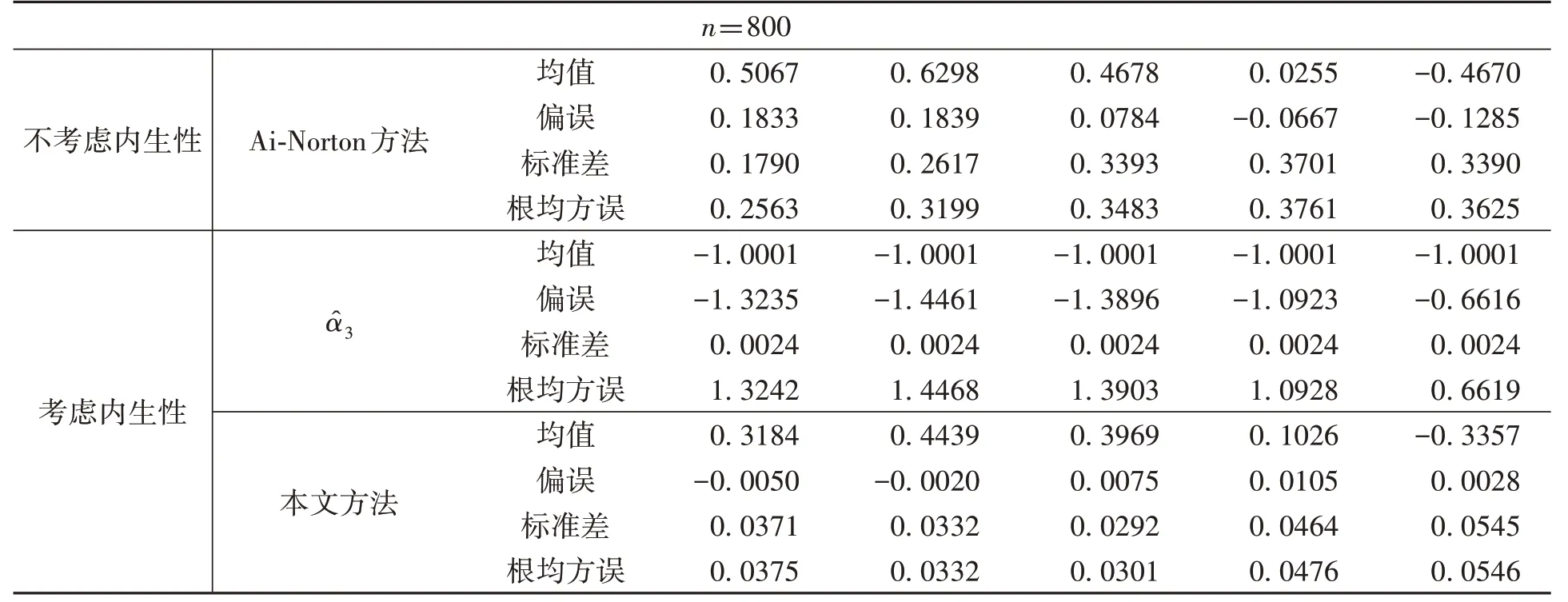
續表

我們還考察了只有x1為內生變量時的模擬，其中數據生成過程為

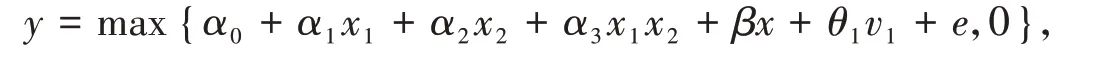
除x2= 1+ 2x+ 2z2外，各參數和其他變量同前。x1，x2真正交互效應的計算與前類似，只是去掉與v2有關的項和積分。結果表明（此處從略），前述模擬結論不變。

四、風險資產配置比例內生模型的Tobit分析

家庭風險資產配置會受到家庭對外關系的影響，也會受到家庭利用新型信息化渠道（如財經APP、互聯網）獲得財經信息情況的影響。Hong et al.（2004）的研究表明，家庭與鄰居溝通密切或去教堂頻率較高，會提升家庭參與股票投資的可能性。Bertaut and Haliassos（1997）、Bogan（2008）均認為，互聯網或計算機的使用會降低家庭股票市場參與成本，從而提升家庭股票市場的參與概率。在中國家庭金融情境下，家庭對外關系與對新型信息工具的使用對家庭風險資產配置比例的邊際影響怎樣呢？另外，家庭對外關系與家庭對新型信息工具的使用在影響家庭風險資產配置中的交互效應是怎樣的呢？

新型信息化工具（如財經APP、互聯網等）作為當前人們普遍應用、流行的獲取財經信息的途徑，可能會促進傳統的家庭對外關系對風險資產投資的影響，因為新型信息化工具是對現有面對面交流以及電話聯絡的延伸，會促進家庭對外關系的發展（Wellman et al.，2001），所以，它與家庭對外關系在影響風險資產投資方面可能相互促進。不過，Nie and Hillygus（2002）認為，互聯網在一定程度上會降低人們社會活動的頻率，對家庭對外關系具有消極作用。因此，新型信息化工具的使用也有可能會削弱家庭對外關系對風險資產投資比例的影響，使兩者間的影響互為削弱。

多項研究表明（如：吳衛星和齊天翔，2007；宗慶慶等，2015；Chen and Ji，2017），戶主年齡對家庭風險資產（如股票）投資具有倒U 型影響，即家庭參與股市的可能性或投資份額隨戶主年齡的增加呈邊際遞減規律。作為本文方法的應用，我們還探討年齡對家庭風險資產配置比例的邊際影響和平方效應。為此，我們設定如下角解型Tobit模型：

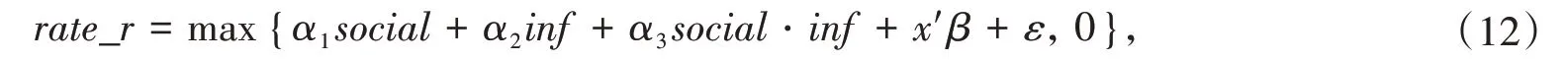
這里，被解釋變量rate_r是家庭風險資產配置比例，social是家庭對外關系變量，inf是家庭新型信息化工具使用情況變量，social?inf是兩者的交互項，x是其他控制變量（包括年齡及年齡的平方），ε是擾動項。

本文使用中國家庭金融調查（CHFS）最新公布的2017年調查數據樣本進行研究。我們將調查中的股票、債券、基金、衍生品、金融理財產品、非人民幣資產和黃金等價值之和作為風險資產價值，它占家庭總資產的比重定義為風險資產配置比例，作為被解釋變量。

家庭利用新型信息化渠道（如財經APP、互聯網等）獲得財經信息的情況是CHFS 早年調查問卷（2011、2013 和2015 年）所不具有的內容，這種新媒介對家庭資產配置的影響的研究具有時代感。我們定義家庭新型信息化工具使用情況變量inf為二值選擇變量D的傾向得分，其中D的定義為：如果對題項“您關注財經類新聞的渠道是什么？”的回答是“財經類APP”或“互聯網、手機等網頁瀏覽”，則D＝1，否則＝0。具體地，將二值變量D關于“您目前是否使用智能手機”二值變量iphone、“是否有網購經歷”二值變量onlineshop、“家庭是否使用手機”二值變量cell、“去年家庭每月平均水、電、燃料、物業管理、暖氣等費用支出”we_fee以及其他外生控制變量x進行Probit 回歸，我們將其傾向得分值定義為新型信息化工具使用情況變量inf。這里不用二值變量D，而用其傾向得分變量inf作為模型（12）的解釋變量，目的之一是削除或減少inf變量在模型中的內生性（本質上，二值變量iphone、onlineshop為其工具變量，而cell和we_fee為social的工具變量，定義見下文）。另一目的是對家庭新型信息化使用程度作一定量刻畫，使之成為一個在0和1之間的連續變量。

對于家庭對外關系變量social，我們選用題項“去年您家庭因春節、中秋節等節假日收入（包括壓歲錢、過節費）和紅白喜事收入（包括做壽、慶生等）”之和的對數刻畫。類似做法見Chen and Ji（2017）等。較強的家庭對外關系可能對家庭風險資產配置有一定的促進作用，但家庭在風險資產投資（如股市投資）中也有可能與其他參與者建立關系，使social與模型（12）中的擾動項具有一定的相關性，從而具有潛在的內生性。我們選取其工具變量為iphone、onlineshop、cell和we_fee。這樣選取工具變量的理由是：首先，手機是家庭與外界溝通、獲取信息的重要渠道，是否使用手機與家庭對外關系具有相關性，但同時，是否使用手機不會直接影響家庭風險資產配置決策；其次，家庭水電費支出與家庭對外關系（人情禮金/請客吃飯）有一定程度的關聯，但與家庭風險資產配置決策一般沒有直接關系。

為避免信息重復，我們僅保留受訪者是戶主的家庭個體樣本。在清除含有變量數據缺失值和一些不合理數據的個體后，我們共得到37 794 個家庭觀察的樣本，其中31 641 個家庭沒有風險資產投資，被解釋變量rate_r取值0（即家庭沒有進行風險資產投資）的比率為83.7%。由變量的描述統計知，家庭風險資產配置比例平均僅為1.3%，可見，中國家庭對風險資產投資的份額相當低。

表2（II）和（III）給出IV-Tobit 和控制函數方法估計結果，為對照起見，（I）列出Tobit 回歸結果。由（II）的Wald外生性檢驗和（III）的控制函數檢驗，social均具有顯著的內生性。家庭對外關系變量與新型信息化工具使用變量的系數估計均顯著為正，交互項系數顯著為負。不過，由（6）和（7）式知，家庭對外關系與新型信息工具使用對家庭資產配置比例的邊際影響是否也為正，兩者的交互效應是否還為負，它們是否具有顯著性，還不一定。具體結論需由（6）至（8）式估計和檢驗而得。另外，列（II）對其他控制變量的系數估計的符號與預期一致。特別地，戶主年齡對家庭風險資產配置比例模型潛回歸函數的影響具有邊際遞減的特征，它對風險資產配置比例的影響是否也具有邊際遞減特征，需由第二部分中注2的方法判斷。以下分別考察這些問題。

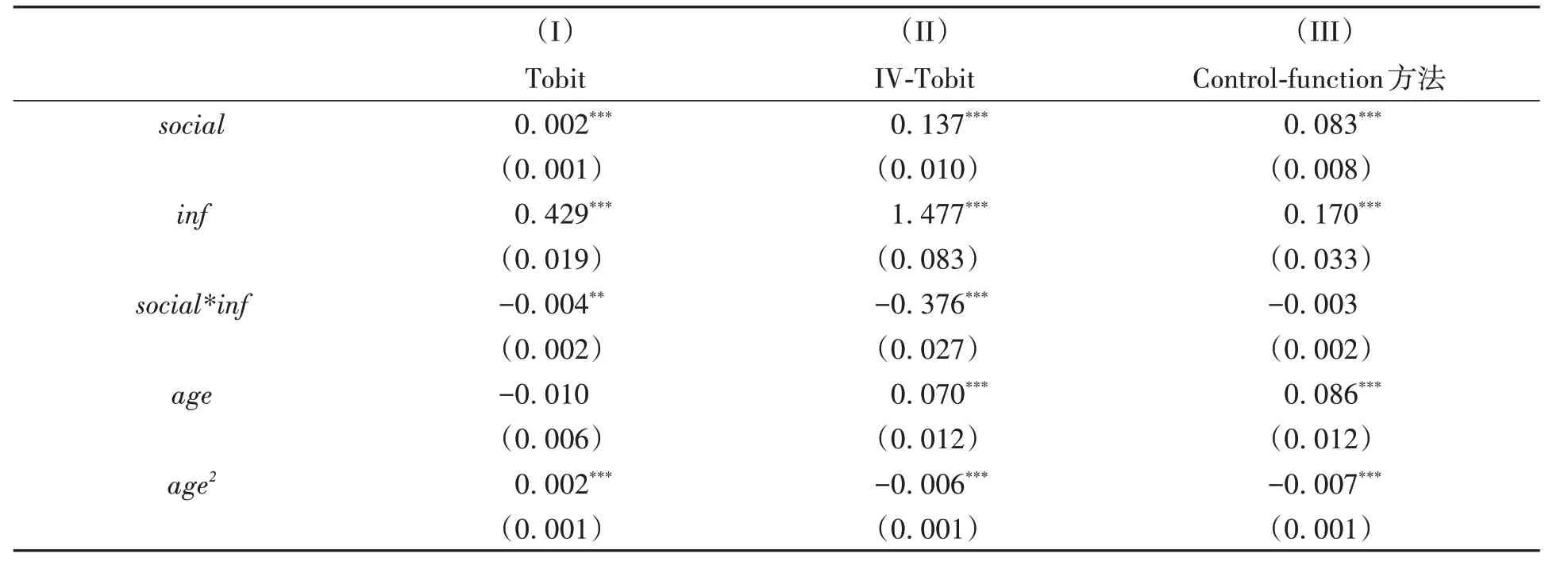
表2 家庭風險資產配置比例Tobit模型的估計結果

續表

（一）家庭對外關系與新型信息工具使用的邊際影響和交互效應

由表2（III）控制函數方法估計結果，并利用（6）（7）式，我們逐個計算家庭對外關系與新型信息工具使用對家庭風險資產配置比例的邊際影響、交互效應在各樣本觀察點處的值。圖1 給出它們關于被解釋變量rate_r擬合值的散點圖。

由圖1（A）知，social和inf對風險家庭資產配置比例的邊際影響在所有觀察點處均為正，與表2中social和inf系數估計為正的結論一致。由圖1（B）知，social和inf影響家庭風險資產配置比例的交互效應在大多數觀察點處均為正（只在少部分觀察點處為負），這與表2（II）中social和inf交互項的系數估計為負的結論不完全一致。可見，social和inf的邊際影響及交互效應具有個體異質性，僅依IV-Tobit 估計中交互項系數的大小、符號和顯著性，對交互效應進行分析和推斷是不恰當的。

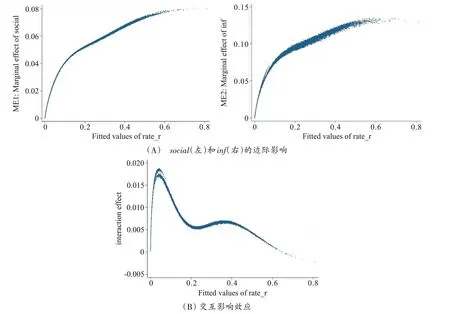
圖1 social和inf邊際影響和交互效應的散點圖

表3 報告social和inf的邊際影響、交互效應的樣本觀察值的描述統計結果。平均來看，social和inf對家庭風險資產配置比例的邊際影響均為正，兩者交互效應也為正。在不同分位點處，social和inf的邊際影響均也為正；兩者的交互效應在最小值處為負，其他分位點處均顯著為正。

我們采用自助法對邊際影響、交互效應均值是否等于零的原假設進行檢驗，其中對樣本進行500次重抽樣，結果見表4。平均來看，social和inf對家庭資產配置比例的邊際影響均顯著為正；兩者的交互效應顯著為正。正的交互效應說明，新型信息化對家庭對外關系影響資產配置比例的效應具有正向調節作用；同樣，對外關系對新型信息化影響資產配置比例的效應也具有正向調節作用。

表3 邊際影響和交互效應的統計描述

表4 平均邊際影響與交互效應的Bootstrap結果

（二）年齡的邊際影響和平方效應

由表2（II）估計知，年齡及其平方項的系數估計分別為正和負，即年齡對潛回歸函數的影響滿足邊際效用遞減規律。我們使用前述方法（9）估計年齡對家庭風險資產配置比例的邊際影響和平方效應在各樣本點處的值。圖2給出它們關于年齡的散點圖。可見，age對家庭風險資產配置比例的邊際影響在年齡小于60歲時均為正，而在大于60處時均為負；age的平方效應總小于零。

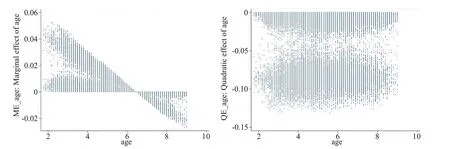
圖2 年齡的邊際影響（左）和平方效應（右）的散點圖

表5報告age的邊際影響、平方效應的樣本觀察值的描述統計結果。平均來看，age對家庭風險資產配置比例的邊際影響為正，其平方效應為負，故年齡影響風險資產配置比例符合邊際效用遞減規律，這與表2（II）中age與age2系數估計的正負相一致。不過，年齡的邊際影響在低分位點處為負，在高分位點處（大于50%）才表現為正。年齡的平方效應除在最大值處為正外，在其他分位點處均為負。

表5 年齡邊際影響、平方效應的統計描述

我們采用自助法對age的邊際影響、平方效應的平均水平進行bootstrap 檢驗，其中進行500 次重抽樣，結果見表6。從平均水平來看，age對家庭風險資產配置比例的邊際影響顯著為正，平方效應顯著為負，進一步驗證了年齡對家庭風險資產配置比例的影響符合邊際效用遞減規律的結論。

表6 age的邊際影響與平均效應平均水平的bootstrap結果

五、總結與啟示

角解型Tobit模型是基于個體最優選擇可能落于選擇空間的邊界上所構建、反映個體變量之間的影響機制，它不同于原模型為線性回歸模型而被解釋變量因為數據歸并而設定的Tobit模型。目前計量經濟方法論文獻沒有給出角解型內生Tobit模型中解釋變量交互效應、平方效應的估計與檢驗方法。

本文給出角解型內生Tobit模型中解釋變量邊際影響、交互效應、平方效應的估計與檢驗方法，推廣了Ai and Norton（2003）在外生解釋變量情形下的相應估計與檢驗。關于交互效應的Monte Carlo數值模擬顯示，我們的估計方法在有限樣本下表現良好，但不當的估計方法會對真實交互效應產生較大的偏誤。

作為應用，我們設定家庭風險資產配置比例Tobit模型，并應用本文方法，估計家庭對外關系與新型信息化工具使用對家庭風險資產配置比例的邊際影響、交互效應，以及年齡對風險資產配置比例的邊際影響和平方效應。總的來看，家庭對外關系與新型信息化工具使用對風險資產配置比例的交互效應顯著為正，新型信息化工具使用對家庭對外關系影響資產配置比例的效應具有正向的調節作用；同樣，家庭對外關系也會促進新型信息化工具使用對風險資產配置比例的影響效應。戶主年齡對家庭風險資產配置比例的邊際影響顯著為正，且平方效應顯著為負，符合邊際效用遞減的規律。

實證研究中我們應區別角解型Tobit 模型和數據歸并型Tobit 模型中解釋變量邊際影響、交互效應、平方效應的估計方法的不同。如果所研究的模型是角解型內生Tobit模型，則我們不可簡單地將IV-Tobit模型中變量、交互項、平方項的系數估計作為變量邊際影響、變量間交互效應、平方效應估計和推斷的依據，也不可使用外生解釋變量情形下的Ai-Norton 方法估計交互效應，而應按本文的估計和檢驗方法去做。在內生情形下角解型Tobit模型中交互效應、平方效應的估計與推斷方法具有廣泛適用性。