Multifractal analysis of the convergence exponent in continued fractions

1 Introduction

The convergence exponent of various sequences appears quite often in the context of the geometry of fractal sets and measures. It was used by Besicovitch and Taylor[1]to study the Hausdorffmeasure and the Hausdorffdimension of cut-out sets, by Hawkes [13] to find the entropy dimension of some random sets determined by L′evy processes,by Dodson [3] to characterize the Hausdorffdimension of certain sets associated with Diophantine approximation, by Wang and Wu [27] to prove Hirst’s conjecture on the Hausdorffdimension of certain sets of continued fractions whose partial quotients lie in a fixed strictly increasing infinite sequence of integers,by Fan, Liao, Ma and Wang [7] to determine the Hausdorffdimension of Besicovitch-Eggleston sets in countable symbolic space, by Durand [4] and Li, Shieh and Xiao [19] to describe the Hausdorffdimension and hitting probabilities of random covering sets, and by Fan, Li and Ma[6] to obtain the Billingsley dimension of the sets of generic points for shift-invariant measures in countable symbolic space.

This paper is concerned with the convergence exponent of the sequence of partial quotients in continued fractions. Recall that each real number x ∈(0,1) admits a continued fraction expansion of the form

We propose to study the multifractal property of the convergence exponent τ(x). Many authors have investigated various exponents related to continued fractions; we refer readers to Jarn′?k[16] for the irrationality exponent, Pollicott and Weiss [23] for the Lyapunov exponent of the Gauss map, Kesseb¨ohmer and Stratmann [18] for Minkowski’s question mark function, Fan,Liao, Wang and Wu [8] for the Khintchine exponent, and Jaffard and Martin [15] for the Brjuno function.

The paper is organized as follows: Section 2 is devoted to presenting our main results and some comments. In Section 3,some basic results of continued fractions and some useful lemmas for calculating the Hausdorffdimension are provided. The proofs of the main results are given in Section 4.

2 Main Results

Let T :[0,1)→[0,1) be the Gauss map, defined as

Then Δ(∞) is of full Lebesgue measure. In other words, Δ(α) is of null Lebesgue measure for any 0 ≤α ＜∞. A typical way of measuring the size of such null sets is to calculate their Hausdorffdimensions.

Theorem 2.1 For any 0 ≤α ＜∞,

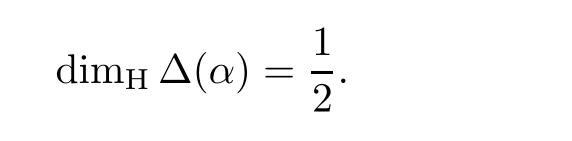
of numbers with strictly increasing partial quotients; see Remark 4.2 below for details.

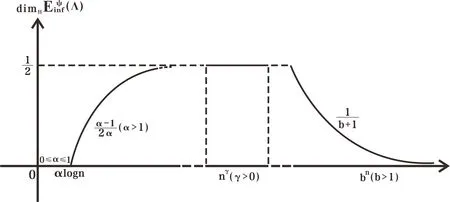
Figure 1 dimH Eψinf(Λ) for different functions ψ

3 Preliminaries

In this section, we first recall some definitions and basic properties of continued fractions,and then present some useful lemmas for calculating the Hausdorffdimension of some sets.

3.1 Elementary properties of continued fractions

3.2 Some useful lemmas

We collect and establish some useful lemmas for estimating the Hausdorffdimension of certain sets in continued fractions. The first lemma is due to Fan, Liao, Wang and Wu [8].

4 Proofs of Main Results

In this section, we give the proofs of main results. Our proofs are inspired by Good [12],Fan, Liao, Wang and Wu [9], Liao and Rams [20].

4.1 Proof of Theorem 2.1

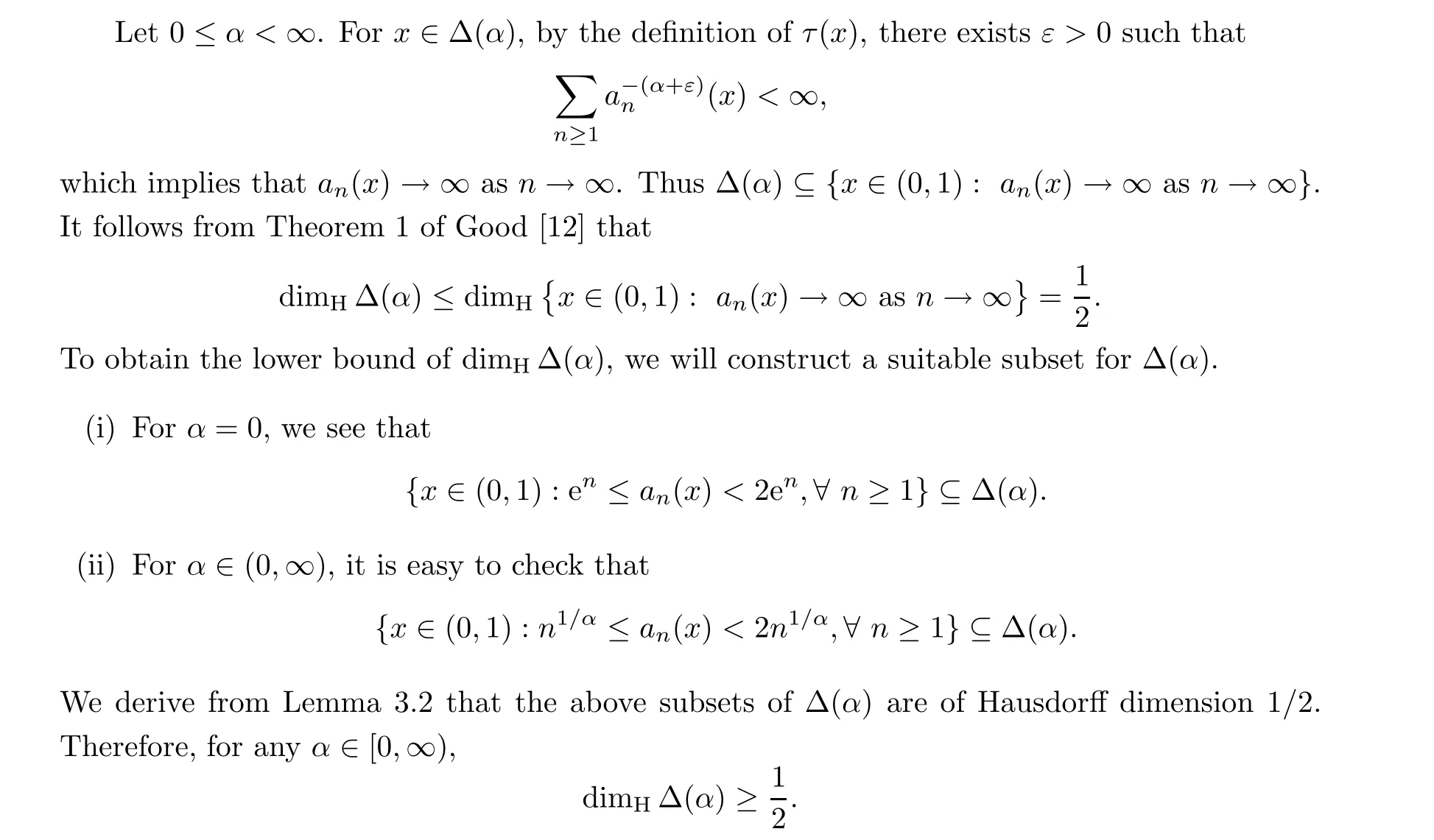
The proof is complete.

4.2 Proof of Theorem 2.4

Observe that, for any n ≥1, the family {I(σ,··· ,σ):k ≥n,(σ,··· ,σ)∈C} is a cover of E(Λ,α). Taking s=ε, and combining (4.1), (4.2) and (4.3), we obtain that

Since s=ε can be made arbitrarily small, we have dimE(Λ,α)=0.

4.2.2 Case 1 ≤α ＜∞

In this case, we will show that

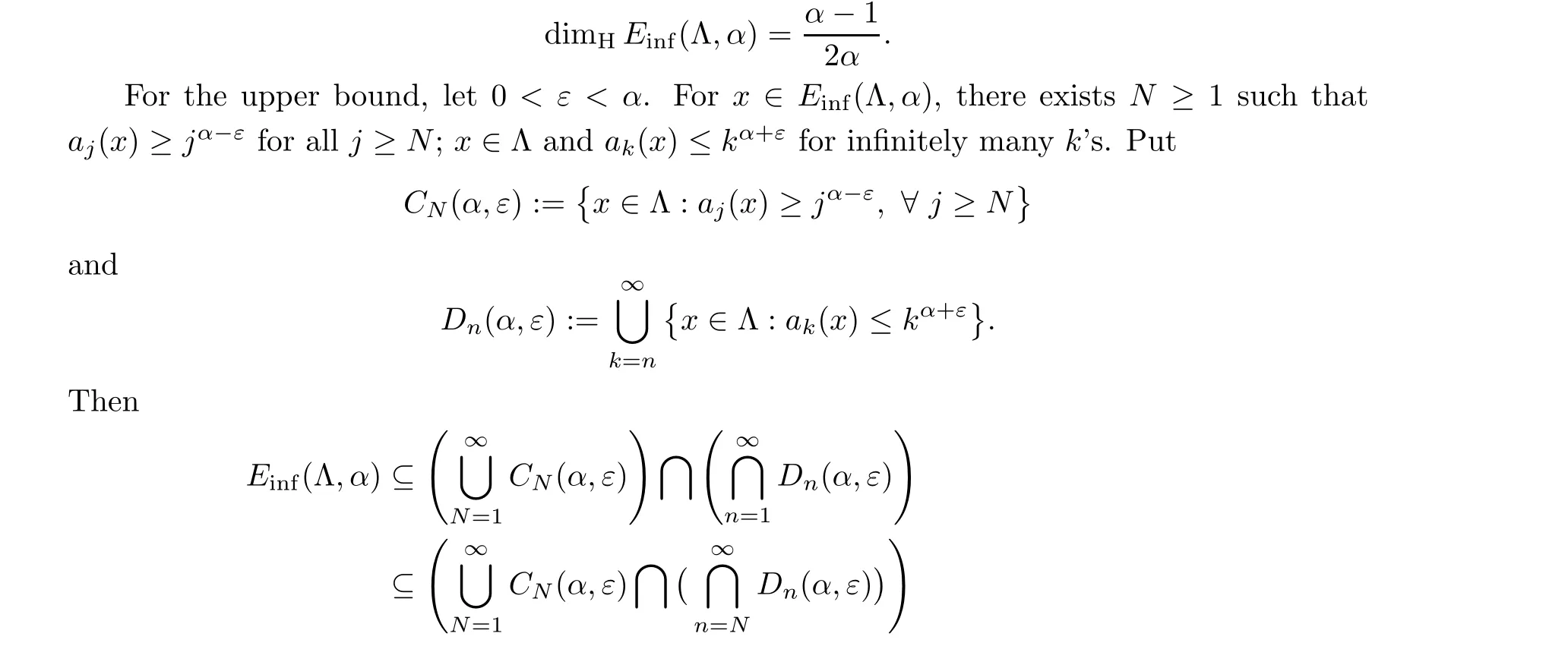
Equivalently,

By Theorem 2.4, the upper bound is trivial, since Λ?Λ. The lower bound can be obtained by similar arguments as to those in the proof of Theorem 2.4 provided above.

4.3 Proof of Theorem 2.5

Acknowledgements The authors would like to thank the anonymous referees for their useful comments and suggestions. The authors are also grateful to Professor Lingmin Liao for his invaluable comments.