基于奇異值分解的圖像壓縮技術①

鄧子云

(長沙商貿旅游職業技術學院 經濟貿易學院,長沙 410116)

圖像壓縮是計算機學科學術界和工程界關注的熱門研究領域之一[1,2].目前已有很多成熟的壓縮算法,也產生了各種圖像壓縮格式,如JPG、GIF 等[3].還有一些通用的文件壓縮算法,進而產生了各種文件壓縮格式,如ZIP、RAR 等[4].奇異值分解方法是線性代數數學學科中一種數據壓縮方法,可以將大規模的矩陣在分解為矩陣的乘法表示后,用一定比例的特征數據矩陣來表示原來的大規模矩陣,從而達到壓縮的目的.奇異值分解方法可以運用到圖像壓縮領域,并起到良好的壓縮效果.

已有一些學者、工程技術人員將奇異值分解方法運用到特定的圖像壓縮應用上,如視頻監控圖像、遙感圖像等[5,6].還有的研究人員結合奇異值分解方法和其它的算法來提升圖像的壓縮比[7],絕大多數研究工作采用的是Matlab 開發工具[8,9].考慮到圖像壓縮算法多已成熟,本文并不打算提出新的算法,而是深入研究基于奇異值分解的技術原理,提出2 種運用奇異值分解作圖像壓縮的方法,用Python 編程實現并展開實驗,再對JPG、PNG 這2 種通用的圖像格式作出壓縮效果的示例和對比分析.

1 奇異值分解的原理

奇異值分解可以針對任意形態的矩陣作特征值分解.現實應用場景中的數據確實不太可能都是方陣,而多是行數、列數不等的數據矩陣,因此,奇異值分解具有廣泛的應用價值[10].

奇異值分解的通用形式如式(1)所示[11–13]:

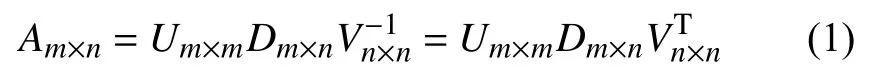
式(1)中的Um×m被稱為左奇異向量組成的標準正交基矩陣,Dm×n被 稱為特征值對角矩陣,被稱為右奇異向量組成的標準正交基矩陣.不論是m＞n,還是m≤n,式(1)都會成立.式(1)可用更為形象的圖形來表述,如圖1(a)和圖1(b)所示[14].

2 用奇異值分解壓縮圖像的原理

根據式(1),如果將r個特征值從大到小排序,并調動對應的Um×m和中的向量位置,可以得到數據矩陣A的奇異值分解排序后的結果,這個分解結果即可用于壓縮數據矩陣A.

2.1 如何壓縮矩陣數據

具體壓縮方法是取前k個特征值,及矩陣Um×m和矩陣中的前k個向量,可得到:

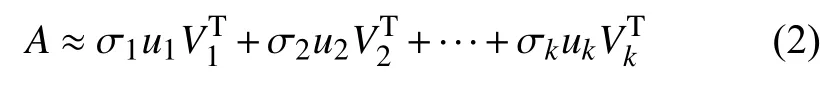
以圖1(a)為例,這種數據壓縮的思想示意如圖2所示.

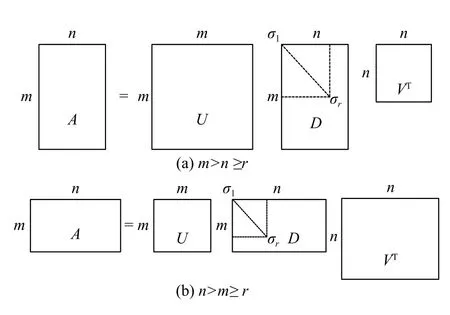
圖1 奇異值分解的圖示

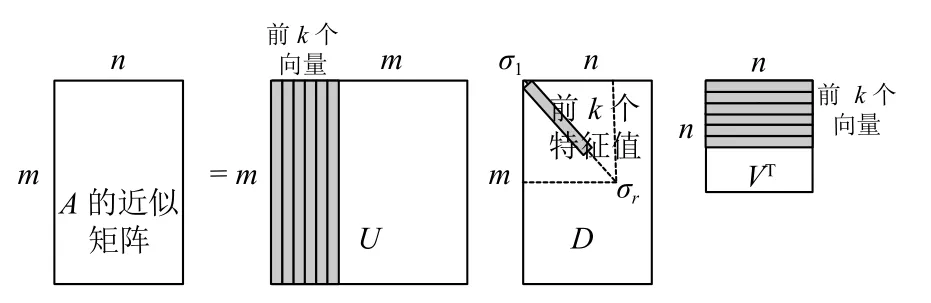
圖2 數據壓縮的思想圖示

這種數據壓縮的思想體現的就是用數據的主要成份來代表整體數據,從而實現只要存儲較少的數據,可見這其實是一種有損數據壓縮,因此需要將數據的壓縮控制在可以接受的范圍[15].

2.2 壓縮比的計算

經過如圖2所示的變換后,數據矩陣A的近似矩陣的行數和列數并沒有變,那又怎么是節約空間了呢?

這是因為奇異值分解后,不必再存儲數據矩陣A,而是存儲矩陣Um×m的前k列、矩陣Dm×n中的前k個特征值,矩陣的前k行,通過式(2)計算再得到數據矩陣A的近似矩陣.這樣,要存儲的數據遠比存儲數據矩陣A要使用的存儲空間少得多.

以一個1000×2000 的數據矩陣為例,則要存儲2 000 000 個數據,假定每個數據占用的存儲空間數量相同.假定運用奇異值分解共需使用50 個特征值來作數據壓縮,存儲矩陣Um×m的前50 列需存儲1000×50=50 000個 數據,存儲矩陣的前k行需存儲2000×50=100 000個 數據,則總計需要存儲50 000+100 000+50=150 050個數據,這遠比存儲2 000 000 個數據要節約存儲空間.

衡量這種節約的程度可用壓縮比來表示,按式(3)所示的公式計算:

式(3)中,P表示壓縮比,S原表示原始數據占用的存儲空間,S壓表示壓縮后的數據占用的存儲空間.因此在上述例子中:

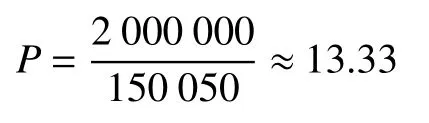
2.3 k 取值的2 種方法

k取值應為多少合適呢?那得看對數據壓縮的目標需求了,k越大,數據就壓縮得越少,需要的存儲空間也越多,需要找到一個合適的平衡點.有2 種方法:

(1)按特征值個數占比閾值取特征值個數.設定一個比例閾值f,如果k與特征值總個數之比的值超過閾值f,則取前k個特征值.

(2)按特征值之和占比閾值取特征值個數.設定一個比例閾值f,如果前k個特征值之和與所有特征值之和的比的值超過閾值f,則取前k個特征值.

2.4 圖像壓縮的原理

以常用的PNG 和JPG 格式的圖像為例,讀取它們的圖像數據可得到一個3 維的數據矩陣.第1 維表示的橫向的像素,第2 維表示縱向的像素,第3 維表示圖像的通道,用0～255 范圍的數據表示數據值.

PNG 和JPG 兩種格式不同的是,PNG 格式圖像的第3 維有4 個通道,分別表示R (Red,紅色)、G (Green,綠色)、B (Blue,藍色)、A (Alpha,透明度);而JPG 格式圖像只有R、G、B 這3 個通道,沒有A 這個通道[16].這也是JPG 格式圖像比PNG 格式圖像占用空間更小的根本原因.此外,兩種格式對數據均有壓縮的算法.這里不討論并忽略兩種格式本身的數據壓縮算法.

在分離得到PNG 格式圖像的R、G、B、A 這4 個通道的數據矩陣后,可對這4 個2 維數據矩陣分別作奇異值分解,再根據使用的k取值的方法和閾值f,可得到這4 個數據矩陣的前k個特征值、Um×k和.JPG 格式圖像則不需要對A 通道的數據矩陣作奇異值分解.

要查看壓縮后的PNG 格式圖像,則可將4 個通道的前k個特征值、Um×k和根據式(2)分別計算得到近似的數據矩陣,組合這4 個2 維數據矩陣形成PNG格式圖像的3 維數據,即可顯示圖像.JPG 格式圖像則計算并組合R、G、B 這3 個通道的壓縮后數據得到圖像的3 維數據.

3 圖像壓縮應用示例

這里以一張原圖的PNG、JPG 2 種格式為例,用k取值的2 種方法來展開圖像壓縮實驗.

3.1 圖像原圖

使用的圖像原圖如圖3所示.

圖3 原圖

原圖寬度為4928 像素,高度為3264 像素,用8 位整數表示各通道的值.則PNG 原圖占用的存儲空間為(不考慮PNG 格式本身的壓縮效果):

4928×3264×4×8=514 719 744 bits ≈61.36 MB

JPG 原圖占用的存儲空間為(不考慮JPG 格式本身的壓縮效果):

4928×3264×3×8=386 039 808 bits ≈46.02 MB

在Python 中,可用代碼1 的源代碼獲取PNG 原圖4個通道數據矩陣.

代碼1.獲取PNG 原圖4通道數據矩陣import numpy as np from PIL import Image#加載圖像,第1 個參數為原圖的完整路徑orignImage=Image.open(r'原圖.png','r')imageArray=np.array(orignImage)#得到R 通道數據矩陣R=imageArray[:,:,0]#得到G 通道數據矩陣G=imageArray[:,:,1]#得到B 通道數據矩陣B=imageArray[:,:,2]#得到A 通道數據矩陣#原圖為JPG 時應注釋此句源代碼A=imageArray[:,:,3]

PIL 為Python 的一個第三方圖像處理類庫,事先應在操作系統的命令界面用語句“pip install pillow”來安裝.

3.2 按特征值個數占比閾值取特征值個數

在Python 中,用代碼2 即可得到一個數據矩陣的奇異值分解結果.

代碼2.數據矩陣奇異值分解import numpy as np#對R 通道數據矩陣作奇異值分解U_R,sigma_R,V_T_R=np.linalg.svd(R)#對G 通道數據矩陣作奇異值分解U_G,sigma_G,V_T_G=np.linalg.svd(G)#對B 通道數據矩陣作奇異值分解U_B,sigma_B,V_T_B=np.linalg.svd(B)#對A 通道數據矩陣作奇異值分解#為JPG 原圖時應注釋此句源代碼U_A,sigma_A,V_T_A=np.linalg.svd(A)

可以發現,在作奇異值分解后,sigma_R、sigma_G、sigma_B、sigma_A 均為一維數組,其元素個數均為3264,則表明均有3264 個特征值.需要注意的是,Python中的0 會表示為一個很小的值,而不會表示為整型的0,因此有的通道數據矩陣可能并沒有3264 個特征值,需要編程判斷,可以用特征值與一個很小的值(如0.0001)比較,如果小于這個很小的值,則將特征時判斷為0.結果發現,sigma_A 的特征值只有1 個.為什么會這樣呢?說明A 通道數據是冗余的.

設計一個函數,用于生成指定的比例閾值下,用通道的壓縮后數據來生成圖像的近似數據矩陣,如代碼3 所示.

代碼3.指定比例閾值下的圖像近似數據矩陣生成#功能:針對某個通道的數據矩陣作奇異值分解得到的U 矩陣、sigma#數組、V_T 矩陣,根據percent(百分比)取前若干個特征值來生成#該通道的近似數據矩陣#參數:U,對某個通道的數據作矩陣奇異值分解后得到的U 矩陣;sigma,#對某個通道的數據作矩陣奇異值分解后得到的sigma 數組;V_T,對#某個通道的數據作矩陣奇異值分解后得到的V_T 矩陣;percent,特#征值個數占比閾值.#返回值:圖像的某個通道的近似數據矩陣def genCompressData(U,sigma,V_T,percent):m=U.shape[0]n=V_T.shape[0]reChannel=np.zeros((m,n))for k in range(len(sigma)):#以得到該通道的近似數據矩陣#逐個累加reChannel=reChannel+sigma[k]*np.dot(U[:,k].reshape(m,1),V_T[k,:].reshape(1,n))

#如果已經超過設定的比例閾值if (float(k)/len(sigma)>percent):#將數據值規范到0-255 范圍內reChannel[reChannel＜0]=0 reChannel[reChannel>255]=255 break#將返回的近似數據矩陣的元素數據類型規范#為uint8 return np.rint(reChannel).astype("uint8")

取特征值個數占比閾值f分別為0.001、0.005、0.01、0.02、0.03、0.04、0.05、0.1.可用代碼4 逐個形成并保存壓縮后再生成的圖像.

代碼4.形成并保存過程for p in [0.001,0.005,0.01,0.02,0.03,0.04,_0.05,0.1]:#生成R 通道近似數據矩陣reR=genCompressData(U_R,sigma_R,V_T_R,p)#生成G 通道近似數據矩陣reG=genCompressData(U_G,sigma_G,V_T_G,p)#生成B 通道近似數據矩陣reB=genCompressData(U_B,sigma_B,V_T_B,p)#生成A 通道近似數據矩陣,為JPG 原圖時應注釋此句源代碼reA=genCompressData(U_A,sigma_A,V_T_A,p)#生成完整的近似數據3 維矩陣,原圖為JPG 時則轉而使用下面的#注釋語句reI=np.stack((reR,reG,reB,reA),2)# reI=np.stack((reR,reG,reB),2)reI=np.stack((reR,reG,reB,reA),2)Image.fromarray(reI).save("{}".format(p)+"img.png")

為簡便起見,取比例閾值f值為0.001、0.01、0.05、0.1 時的4 幅壓縮效果圖作出展示,如圖4所示.從圖中可以看出,比例閾值f值為0.001 圖不清楚,為0.01 值時可以大致看出輪廓,為0.05 時圖像基本可辨,為0.1 時圖像與原圖相差無幾,人眼分辨不出是否壓縮過.

對JPG 格式圖像的實驗結果這里不再重復羅列分析.在計算出取不同的比例閾值下的壓縮比后,列出結果如表1所示.

從表1可以看到,即使是取比例閾值f為0.1,壓縮比都還能達到5.99,因此,壓縮效果良好.如果對壓縮后的圖像清晰度要求可以降低,則還可以得到更高的壓縮比.

表1中的兩種格式的圖像的壓縮比相同的原因是,不管是3 個通道還是4 個通道,在同一比例閾值下,針對各個通道取特征值的個數相同,故壓縮比就會相同.

圖4 按特征值個數占比閾值取特征值個數時的壓縮效果圖

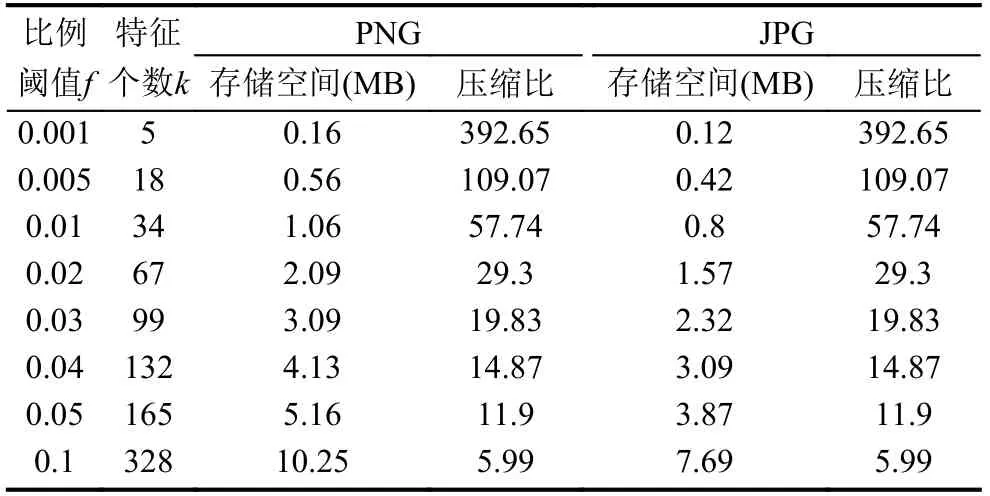
表1 按特征值個數占比閾值取特征值個數時的壓縮比(4 個通道均相同)

3.3 按特征值之和占比閾值取特征值個數

設計一個函數(代碼5),用于生成指定的比例閾值下,用各通道的壓縮后數據來生成圖像的近似數據矩陣.

代碼5.圖像近似數據矩陣生成#功能:針對某個通道的數據矩陣作奇異值分解得到的U 矩陣、sigma#數組、V_T 矩陣,根據percent(百分比)取前若干個特征值來生成#圖像的該通道的近似數據矩陣;#參數:U,對某個通道的數據做矩陣奇異值分解后得到的U 矩陣;#sigma,對某個通道的數據作矩陣奇異值分解后得到的sigma 數組;#V_T,對某個通道的數據作矩陣奇異值分解后得到的V_T 矩陣;

#percent,特征值之和占比閾值.#返回值:圖像的該通道的近似數據矩陣def genCompressDataFromSum(U,sigma,V_T,percent):m=U.shape[0]n=V_T.shape[0]reChannel=np.zeros((m,n))sum=0.0 #sum 為特征值總和for i in sigma:sum+=i# sumcurrent 為已累加的特征值的和sumcurrent=0.0 for k in range(len(sigma)):#逐個累加,以得到該通道的近似數據矩陣reChannel=reChannel+sigma[k]*np.dot(U[:,k].reshape(m,1),V_T[k,:].reshape(1,n))#累加特征值sumcurrent+=sigma[k]#如果已經超過設定的比例閾值if (sumcurrent/sum>percent):#將數據值規范到0-255 范圍內reChannel[reChannel＜0]=0 reChannel[reChannel>255]=255 break#將返回的近似數據矩陣的元素數據類型規范為uint8 return np.rint(reChannel).astype("uint8")

取特征值之和占比閾值f分別為0.5、0.6、0.7、0.8、0.9,可用代碼6 逐個形成并保存壓縮后再生成的圖像.

代碼6.形成并保存過程for p in[0.3,0.4,0.5,06,0.7,0.8,0.85,0.9]:#生成R 通道近似數據矩陣reR=genCompressDataFromSum(U_R,sigma_R,V_T_R,p)#生成G 通道近似數據矩陣reG=genCompressDataFromSum(U_G,sigma_G,V_T_G,p)#生成B 通道近似數據矩陣reB=genCompressDataFromSum(U_B,sigma_B,V_T_B,p)#生成A 通道近似數據矩陣,為原圖JPG 時應注釋此句源代碼reA=genCompressDataFromSum(U_A,sigma_A,V_T_A,p)#生成完整的近似數據3 維矩陣,原圖為JPG 時則轉而使用下面的#注釋語句reI=np.stack((reR,reG,reB,reA),2)# reI=np.stack((reR,reG,reB),2)#保存圖像,參數為圖像的完整路徑Image.fromarray(reI).save(“{}”.format(p)+“img.png”)

為簡便起見,取比例閾值f值為0.6、0.7、0.8、0.85 時的4 幅壓縮效果圖作出展示,如圖5所示.可以看到,當比例閾值f值為0.7 時,已基本可辨;當比例閾值f值為0.85 時,圖片已經比較清晰.表2還給出了取不同的閾值f值時,對應的各個通道的特征值個數,以及針對PNG 格式圖像、針對JPG 格式圖像的存儲空間和壓縮比.

表2中PNG 格式圖像的存儲空間和JPG 格式圖像的存儲空間相同,且A 通道的k值為1 的原因是,PNG格式圖像原圖的A 通道中的值都是等值的255,相當于這個通道的數據是冗余的,其圖片顯示效果與JPG 格式圖像相當.

圖5 按特征值之和占比閾值取特征值個數時的壓縮效果圖

3.4 壓縮比變化趨勢分析

根據表1和表2,作比例閾值和壓縮比之間的關系圖,如圖6所示.

從圖6(a)來看,對PNG 格式圖像的壓縮比和對JPG 格式圖像的壓縮比的變化曲線相同.在比例閾值為0.01 時出現曲線拐點,這表明在前1%的特征值里,較大值的特征值比較集中;之后曲線變緩,在比例閾值為0.1 以后,曲線已經非常平緩,表明增加特征值已很難再改善圖像質量.

從圖6(b)來看,對JPG 格式圖像的壓縮比要比對PNG 格式圖像的壓縮比低一點.在比例閾值為0.9 后,曲線變得更為平緩,這表明增加特征值已很難再改善圖像質量.

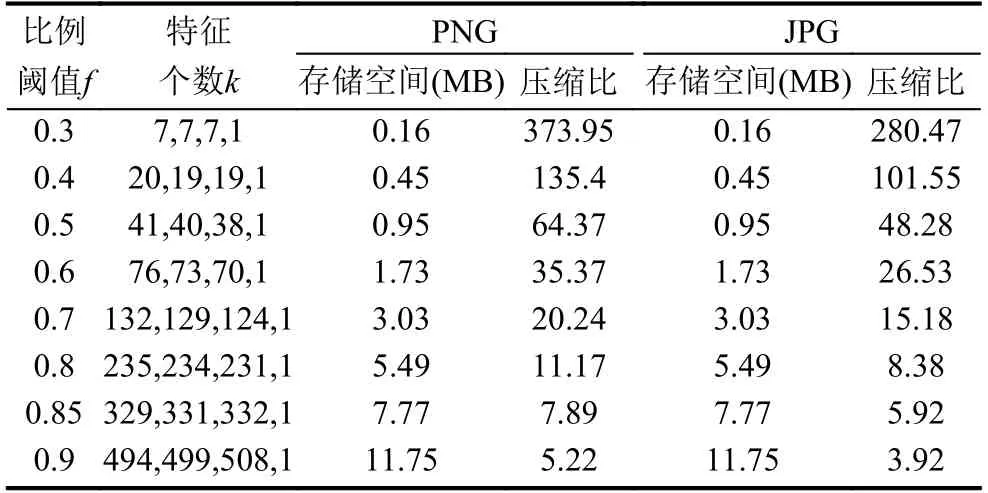
表2 按特征值之和占比閾值取特征值個數時的壓縮比(通道R,G,B,A)

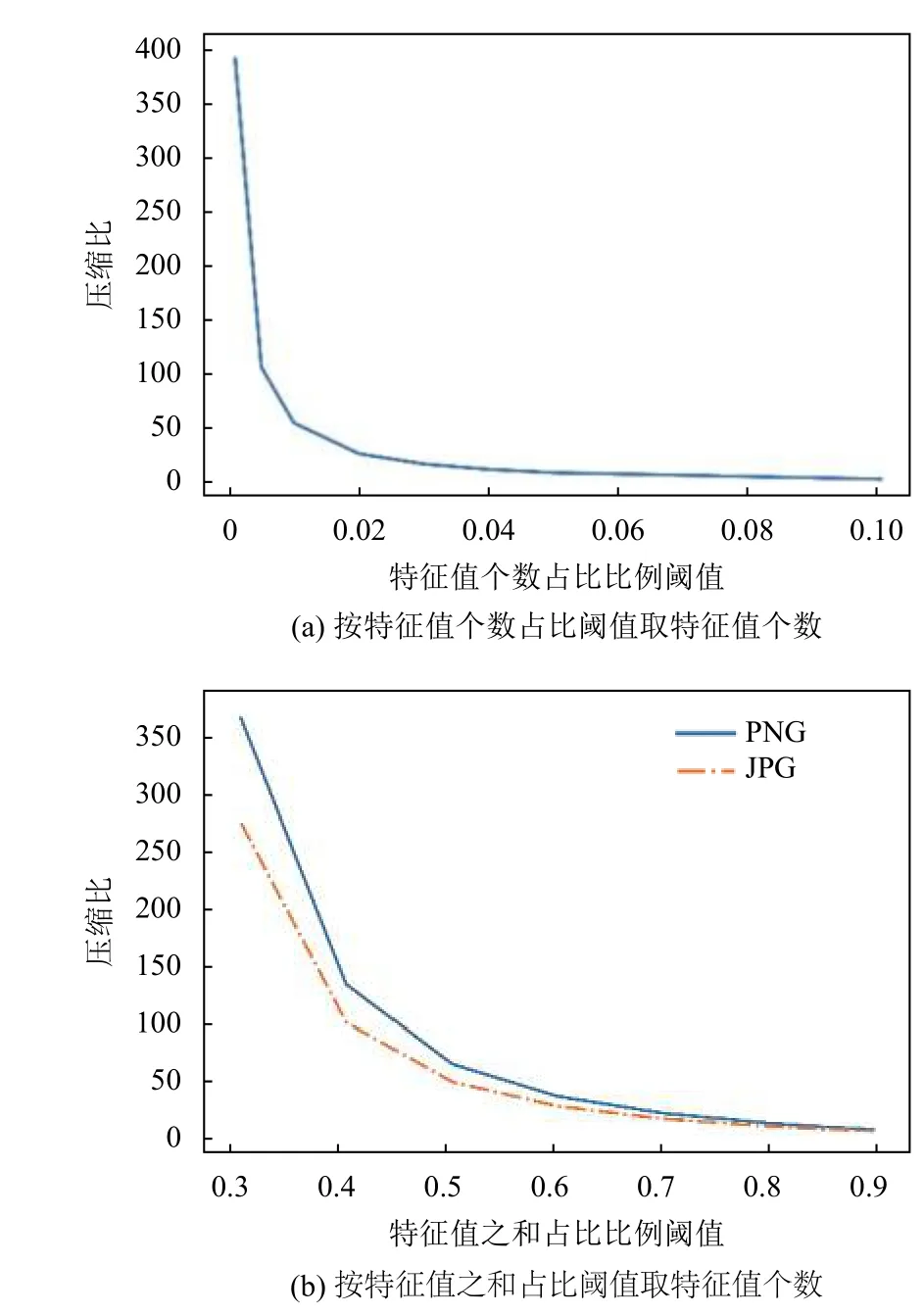
圖6 比例閾值和壓縮比之間的關系圖

相對來說,按特征值之和占比閾值取特征值個數的方法更為實用.因為首先,它考慮的是特征值的重要程度,而不是個數;其次這種方法可以應對個別通道數據冗余的問題.更為重要的是,這種方法可以用于進行大規模數量的圖像文件壓縮,因為這種方法可以劃定一個統一的可以接受的特征值之和占比閾值,這個閾值就直接代表著圖像的清晰度.鑒于前述對占比閾值的分析,認為這個統一的占比閾值如要基本可辨取0.7,如要比較清晰取0.85.但按特征值個數占比閾值取特征值個數的方法不能劃定一個統一的比例閾值,因為在同一個閾值下,不同的圖像文件的清晰程度可能不同.

3.5 壓縮算法對比分析

現已有很多經典的圖像壓縮算法.以經典的PNG[5]、JPG[6]圖像格式為對比,仍以本文的圖片作為示例,與本文的壓縮方法在壓縮比上的對比分析如表3所示.由此可見,在對PNG 按特征值之和占比閾值取特征值個數(f=0.7)時可以取得最高的壓縮比.

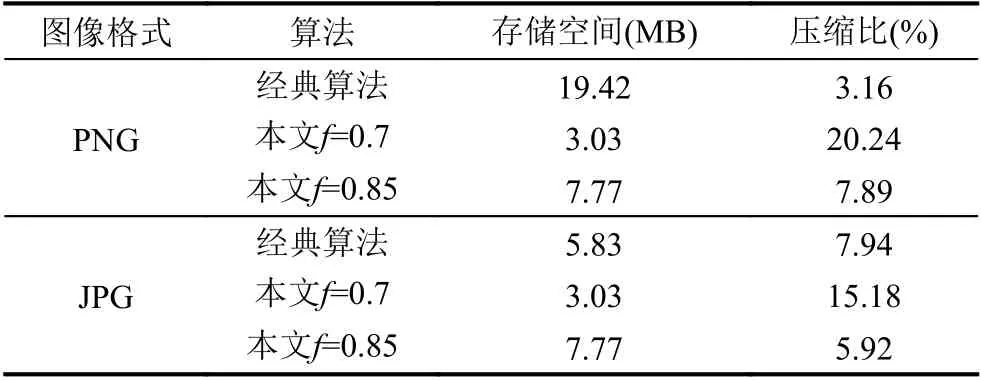
表3 對不同圖像格式處理算法的壓縮比對比

鑒于各種算法的原理不同,Python 已經提供了成熟的軟件包PIL,直接用保存功能即可將圖片存儲為JPG或PNG 格式,不便計算時間效率.而本文給出的算法關鍵之處在于做奇異值分解所耗費的時間,仍以本文的圖片作為示例,實驗結果如表4所示.可見,對JPG 做奇異值分解效率明顯較高,但顯然處理一個圖片已超過1 分鐘,效率有待提升.

表4 奇異值分解時間效率

4 結束語

通過奇異值分解,可以得到3 個分解結果,即左奇異向量組成的標準正交基矩陣Um×m、特征值對角矩陣Dm×n、右奇異向量組成的標準正交基矩陣.有按特征值個數占比閾值取特征值個數和按特征值之和占比閾值取特征值個數2 種方法來做圖像壓縮,從而得到Dm×n中的前k個特征值、Um×m的前k列、的前k行作為要存儲的數據來代表數據矩陣.通過對PNG、JPG 兩種格式圖像作壓縮實驗發現,在本實驗個例中,特征值個數占比閾值取0.1 時,圖片清晰,壓縮比達到5.99;特征值之和占比閾值取0.85 時,圖片清晰,對PNG 格式圖像的壓縮比達到7.89,對JPG 格式圖像的壓縮比達到5.92.認為相對來說,按特征值之和占比閾值取特征值個數的做法更為實用,可用于大規模數量的圖像文件壓縮.

本文研究的局限性在于僅限于奇異值分解本身并應用于圖像壓縮領域,沒有將奇異值分解和其它壓縮算法相結合開展研究.下一步的研究可結合包括奇異值分解在內的多種壓縮算法提出新的組合算法,并作大規模數量的圖像文件處理實驗、對比分析,以尋求具有更高壓縮比、能普適應用的圖像壓縮方法.