基于損傷分析的空心板橋荷載橫向分布系數研究*
錢若霖, 蘇佩, 楊謙
(1.陜西工業職業技術學院 土木工程學院, 陜西 咸陽 712000;2.中聯西北工程設計研究院, 陜西 西安 710000)
裝配式空心板橋預制方便,構造簡單,受力明確,在公路和市政橋梁中應用廣泛。但車輛的反復荷載和外界環境侵蝕使空心板橋的梁體和鉸縫病害增加,這兩種結構損傷會使梁體剛度和梁間傳力有所削弱,進一步影響上部荷載在各片主梁上的分配。周穎針對小箱梁橋的裂縫參數外觀特征,結合剛度模型分析數據,推導了靜、動剛度折減系數,并通過靜、動力狀態下裂縫參數特征值與靜、動剛度折減系數,分別回歸得到了靜、動剛度折減系數與對應裂縫參數之間的關系式,分析了靜剛度與動剛度退化規律及兩者間的關系;聶瑞鋒等針對在役空心板橋,以關鍵參數為自變量、彎矩橫向分布系數為因變量,采用多元非線形回歸得出了彎矩橫向分布系數計算公式,其中鉸縫損傷程度采用鉸縫失效長度與計算跨徑的比值進行量化。該文沿用傳統鉸接板法理論基本假設,將空間問題轉化為平面問題,考慮既有空心板橋服役期間梁體和鉸縫同時損傷情況,對鉸接板法進行參數修正,重新推導荷載橫向分布計算方法,為損傷橋梁承載能力評估提供依據。
1 損傷參數的定義
1.1 鉸縫傳力削減
對于空心板之間通過鉸縫連接的多梁式板橋結構,設有單位正弦荷載作用在1#空心板軸線上,沿鉸縫處縱向切開,每一切縫處引入大小相等、方向相反的剪力gi。圖1為鉸接板橋的基本體系。

圖1 鉸接板法的基本結構
計入鉸縫損傷情況,剪力傳遞會發生削減,引入剪力折減系數μ,考慮到每處鉸縫損傷程度不一,假設各鉸縫折減系數依次為μ1,μ2,μ3,…。根據力法原理,其表達式為:
[δ]{X}+{Δ}=0
(1)
式中:δ為計算系數,即單位力在i處引起的變位,按式(2)計算;X為鉸縫處剪力,按式(3)計算;Δ為外荷載p在i處引起的變位,按式(4)計算。
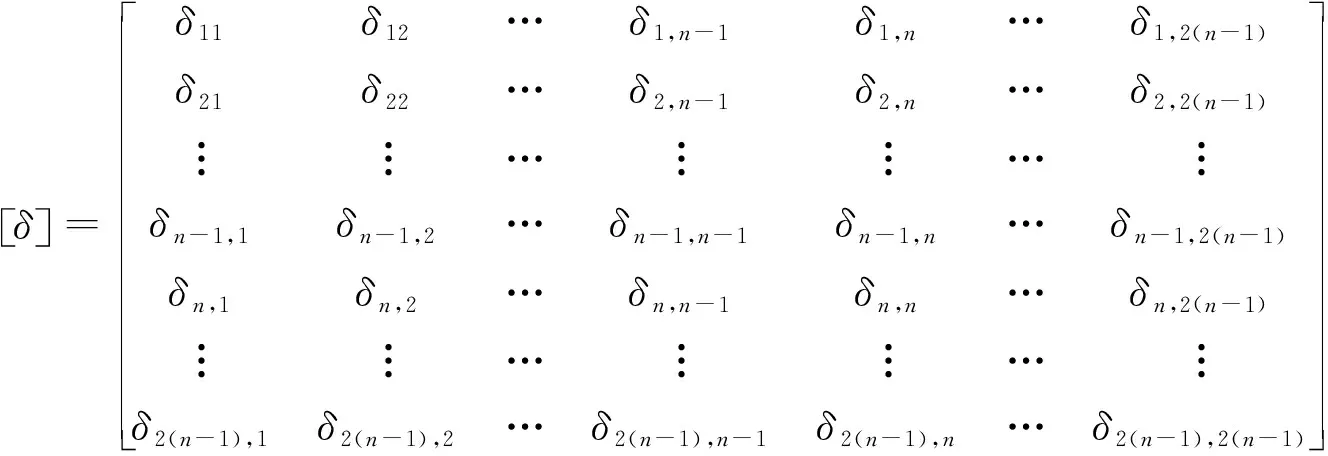
(2)

(3)
(4)
1.2 主梁損傷削減
結合梁體外觀檢測,結合文獻[4]中裂縫參數特征對空心板的靜剛度損傷折減情況進行量化評估。引入裂縫寬度系數θ和裂縫高度系數λ,公式如下:
(5)
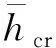
梁體的靜剛度折減系數ξ采用下式計算:
(6)
根據各片板梁剛度實際退化情況,得到剛度折減系數ξ1,ξ2,…,ξn。損傷后梁體剛度評估值Ei按下式計算:
Ei=ξiE
(7)
式中:ξi為剛度折減系數,0<ξi≤1;E為原梁體的剛度。
剛度變化必然影響力法方程變位系數改變,由梁的撓曲線微分方程和扭轉理論可推得簡支梁跨中產生的豎向撓度和扭轉角。x=l/2時,單位荷載作用在剛度發生損傷板梁中央所產生的撓度w為:
(8)
扭矩為b/2sin[(2x)/l],x=l/2時,單位扭矩對剛度損傷板梁產生的截面扭轉角φ為:
(9)
式中:b為板寬;l為橋梁縱向跨度;I為抗彎慣矩;G為抗扭慣矩,G=0.425E。
考慮到每片板的撓度、轉角均受剛度E和折減系數ξi的影響,統一起見,引入變位系數矩陣[δ]的轉化系數ki,ki=1/ξi。
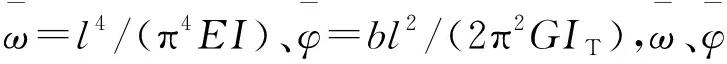
2 修正的鉸接板法方程建立及求解
根據力與變形之間的關系可確定上述正則方程中的常系數值并規定其正負,變位與贅余力素正向一致時取正值,反之取負值。如圖2所示,單位鉸接力下變位的表達式為:
(10)
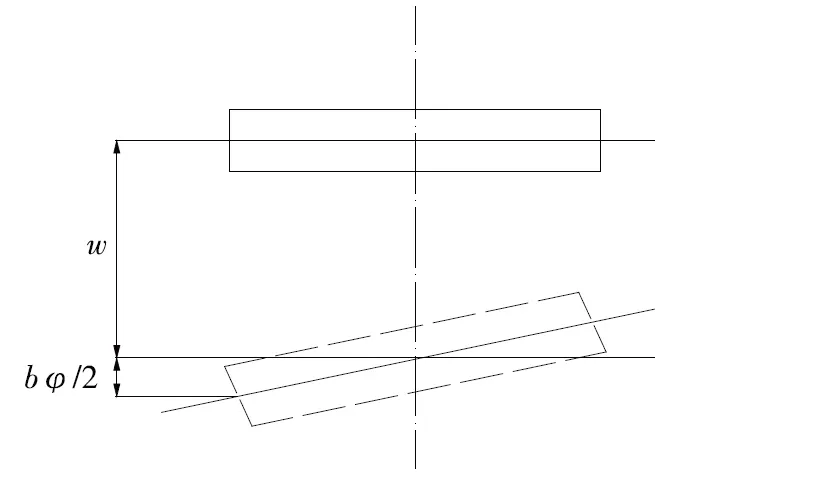
圖2 變形示意圖
外荷載p作用在i號梁時,有:
(11)
(12)
(13)
將各項系數代入第一節力法方程中,編程計算gi,然后根據鉸縫傳力折減系數μi求得實際剪力值如下:
單位荷載作用于1#梁時,橫向分布系數豎標值如下:
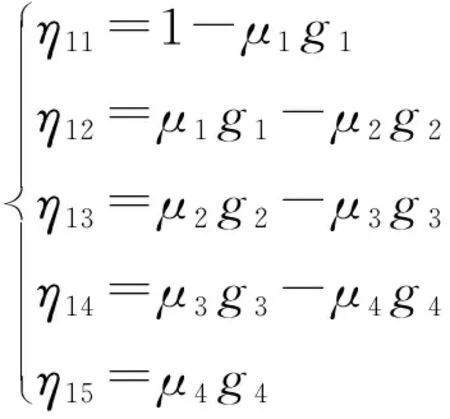
(14)
同理可得其他各梁豎標值。
3 算例分析
某在役裝配式空心板橋上部結構由9片預應力空心板組成,跨徑13 m,采用C50砼。由于鋼筋對截面的剛度貢獻較小,為便于和理論分析統一和對比,仿真建模時不考慮預應力鋼筋、普通鋼筋及鋪裝層作用。空心板標準橫斷面見圖3。
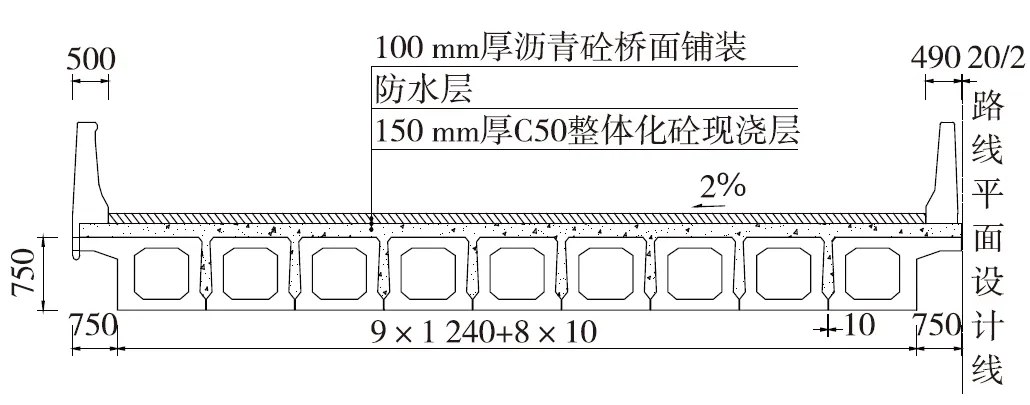
圖3 空心板標準橫斷面(單位:cm)
為精確模擬鉸縫損傷和梁體剛度損傷,采用ANSYS建立實體單元模型進行仿真分析,單元類型為Solid65,根據損傷定義不同構造處的材料特性進行分析計算。鉸縫損傷的量化評估采用文獻[5]中的公式:
(15)
式中:li為完整未損傷鉸縫長度;l為鉸縫通長,即橋梁跨徑。
實橋損傷后剛度根據該橋裂縫開展情況及參數特征值,通過式(6)計算。剛度折減系數如下:
(16)
式中:Ei為每片板評估剛度;E為原始設計剛度。
讀取每種工況下梁的撓度值,根據下式計算影響線豎標值ηij:
(17)
式中:fi為單工況下某塊板的跨中撓度;∑fi為各板跨中撓度值之和。
為簡化計算,并便于對比分析,假設梁體損傷在同等自然和車輛荷載條件下對稱出現。但實際上各梁板損傷一般非對稱,應視具體情況具體分析。以邊梁1#梁和中梁5#梁為例,計算結果見表1。
從表1可看出:修正鉸接板法所得豎標值與傳統鉸接板法計算結果有出入,荷載施加在某片板時,其變位即豎標值明顯增加,遠離荷載的板其豎標值有所減小;離荷載作用位置越遠,豎標值減小幅度越小。其原因是修正鉸接板法綜合考慮了鉸縫傳力削弱和剛度退化的影響。由于實體單元建模同樣考慮了鉸縫和主梁剛度的損傷,有限元法豎標值計算結果更接近于修正鉸接板法,最大誤差不超過1%。修正鉸接板法與實體仿真建模結果更接近,其計算精度更高。按照修正后的方法對既有損傷橋梁進行受力計算和承載力評估,可為橋梁工程加固的精確計算提供依據。
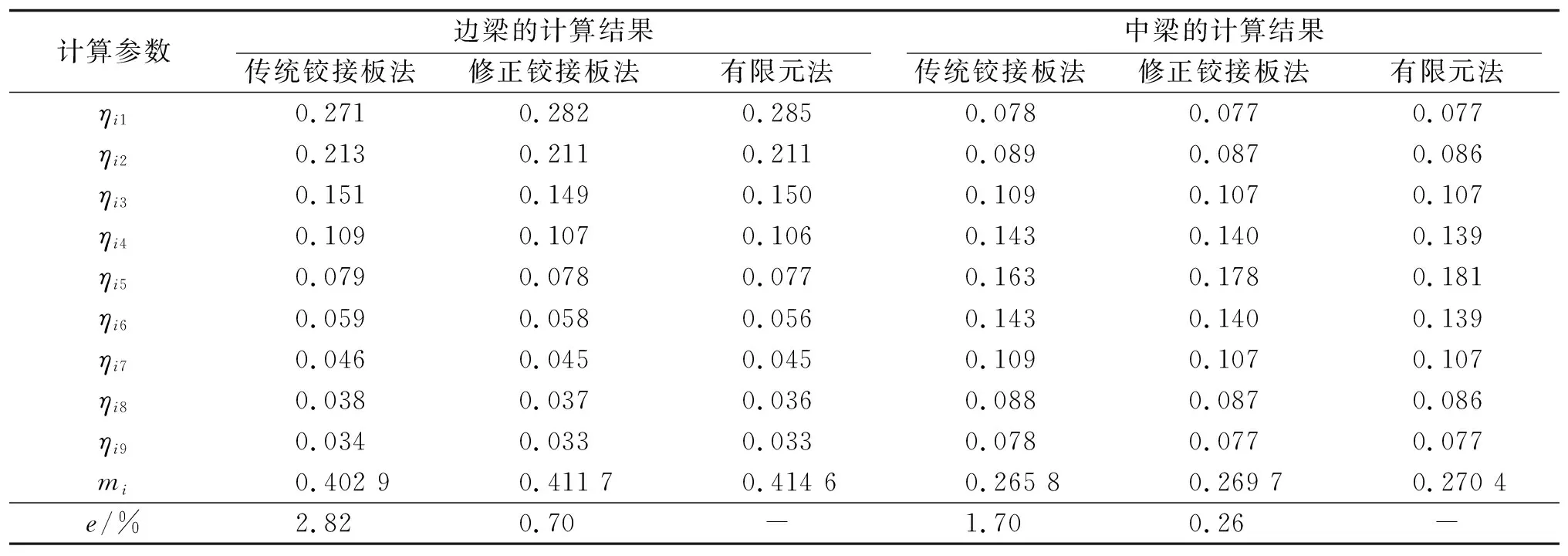
表1 邊梁和中梁影響線豎標及橫向分布系數
4 結論
(1) 考慮鉸縫和梁體損傷的修正鉸接板法的計算結果與有限元分析結果接近。
(2) 對于鉸縫和主梁均發生損傷的在役空心板橋,傳統鉸接板法精度不足;修正鉸接板法綜合考慮了鉸縫損傷和梁體剛度退化的影響,符合在役橋梁實際受力特點,其計算結果更精確。

