面向不平地面的雙足欠驅動步行穩定控制

姚道金 董文濤 王曉明 楊 林

1. 華東交通大學電氣與自動化工程學院，南昌，330013

2. 華中農業大學機電工程系，武漢，430070

0 引言

仿人機器人具有良好的人機交互親和力、對復雜環境的適應性，一直是機器人領域研究的熱點之一[1]。目前針對仿人機器人的研究多集中于結構設計[2]、步態規劃[3]及人機交互[4]等方面。許多著名的機器人被推出：Atlas、ASIMO、“匯童”系列、“悟空”系列等[5]，但機器人在步行過程中，始終存在步態不自然、能耗高等問題[6]。為解決上述問題，近年來，一種更加自然、高效的雙足步行方式——欠驅動步行逐漸成為研究熱點。但步行過程中欠驅動自由度的存在，導致步行控制非常困難，尤其是在不平地面上[7]。

針對不平地面上欠驅動雙足步行，PARK等[8]根據不同步行環境分別設計對應控制器，并使用有限狀態機進行控制器切換，進而實現機器人在不平地面上穩定步行。YADUKUMAR等[7]通過采集分析人類步態數據，并結合混雜零動態的方法，實現AMBER機器人在不平地面上行走。DAI等[9]將地面作為外部擾動，通過增益L2量化機器人對地面干擾的魯棒性，通過魯棒控制實現機器人在不平地面上的行走。NGUYEN等[10]應用兩個周期步態構建機器人步態庫，結合其良好的形態及結構設計，實現機器人在隨機不平地面上的穩定行走。雖然上述算法實現了不平地面上的欠驅動步行，但均基于機器人-地面剛性接觸模型，并未考慮地面柔性對步行的影響，與實際情況不符。在真實環境中，地面由許多柔性材質構成，如木板、橡膠等。隨著日常環境中柔性材料使用的增加，在欠驅動步行控制中，地面柔性不再是一個可以忽略的因素。

目前，許多研究已經證明地面柔性對欠驅動步行產生影響。PLESTAN等[11]發現機器人RABBIT在柔性地面上步行時，地面柔性導致步行能量消耗增加，影響步行穩定性。AGUILAR等[12]通過流體靜力學、動力學分析機器人足部與沙土接觸過程中的運動狀態變化，并從力學角度探討柔性地面上的步行控制問題。為解決地面柔性對步行的影響，一些學者基于Dahl模型[13]、LuGre模型[14]和彈塑性模型[15]等建立了機器人-地面接觸模型，并通過仿真分析了模型參數對步行性能的影響，但上述建模方法較為復雜，在實際機器人系統中應用十分困難，因此，需建立一種便于實際應用的機器人-地面柔性接觸模型。

為實現真實環境中更加高效、穩定的欠驅動雙足步行，需同時考慮地形變化和地面材質變化。本文基于人類變速步行特征，提出一種基于質心運動狀態的步行穩定控制策略，實現不平地面上的欠驅動雙足步行：使用“彈簧-阻尼”系統建立“機器人足部-地面”柔性接觸模型；將三維欠驅動步行解耦為前向和側向的主從控制，通過控制質心位移實現質心速度控制，進而實現機器人穩定步行；最后通過仿真和試驗來證明所提控制策略的有效性。

1 不平地面上機器人建模

機器人足部與地面的接觸模型是機器人步行系統建模的關鍵問題之一。考慮地面柔性，本文將柔性地面等效為一系列由黏彈性單元陣列而成的“彈簧-阻尼”系統[16]，如圖1所示。每個黏彈性單元中地板均通過x、y、z三個方向上“彈簧-阻尼”構件與地基相連，每個“彈簧-阻尼”構件中彈簧剛度系數為k，阻尼系數為c。雙足機器人步行系統是一個強耦合的高度非線性系統，為降低步行系統建模的難度，且便于后續分析與控制，本文忽略三維步行中前向與側向的耦合，使用解耦建模的方式建立機器人步行系統模型。

圖1 雙足機器人在不平地面上行走時數學模型

針對步行前向平面(圖1a)。機器人包括5個自由度q1、q3、q4、q7、q8，其中，q1為欠驅動自由度；機器人大小腿的長度和質量分別為lt、lc和mt、mc，膝關節質量為mk，髖部質量為mH(2個髖關節和腰部質量總和)。機器人步行過程中，支撐足在x、y和z方向上的位移分別為xst、yst和zst，擺動足在x、y和z方向上的位移分別為xsw、ysw和zsw。定義支撐足末端-地面接觸點和髖關節連接線與豎直平面的夾角為θ，機器人步行過程中θ單調增大，可將其作為步行系統的虛擬時間變量。

根據機器人與地面接觸情況，一個完整步行周期可分為單足相和雙足相兩個階段。在步行單足相階段，機器人有且僅有一足與地面接觸，使用拉格朗日建模法得到機器人單足相動力學方程：

(1)

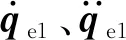
(2)

在機器人步行雙足相階段，支撐足與擺動足均與地面發生接觸，使用拉格朗日建模法，得到前向平面機器人雙足相動力學方程：

(3)

(4)

由式(2)和式(4)得到前向平面一個完整步行周期內機器人動力學模型：

(5)

針對步行側向平面(圖1b)，機器人包括3個自由度q2、q5和q6，髖關節質量為mh，腰部質量和寬度分別為mb和w。與前向平面類似，使用拉格朗日建模法，得到側向平面機器人單足相動力學方程：

(6)

(7)

機器人步行雙足相階段，使用拉格朗日建模法，得到側向平面機器人雙足相動力學方程：

(8)

(9)

由式(7)和式(9)得到側向平面一個完整步行周期內機器人動力學模型:

(10)

2 不平地面上欠驅動步行控制策略

已有研究表明，人類正常步行時質心豎直方向波動為腿長的0.04倍左右，質心在側向波動為腿長的0.033倍左右，前向運動方向為人類主動運動方向，側向運動對前向運動影響忽略不計,因此，三維步行控制可轉化為前向和側向的主從控制[17]。根據“機器人不倒”這一雙足步行穩定性的最直觀表述，筆者已提出一種基于步行速度的欠驅動步行穩定性判定方法：如果機器人步行速度能夠收斂于一個已被證明的可維持步行的速度，則機器人處于穩定狀態[18]。可將機器人質心速度進行分解，分別控制質心速度在前向和側向平面內對理想速度的跟蹤，進而實現機器人欠驅動穩定步行。

在機器人步行前向平面，“機器人-地面”這一復雜的多輸入-多輸出系統可簡化為基于質心位移和質心速度的單輸入-單輸出系統。在控制策略中引入自適應質心位移控制系數，根據地形變化調整該控制系數，修正質心位移，實現前向平面質心速度控制。在步行側向平面，可使用倒立擺模型對步行系統進行簡化，通過控制質心側向位移對前向位移的跟蹤，保證側向平面與前向平面運動相匹配。控制策略結構如圖2所示。控制器根據第j-1周期機器人步行狀態規劃第j周期機器人步態。

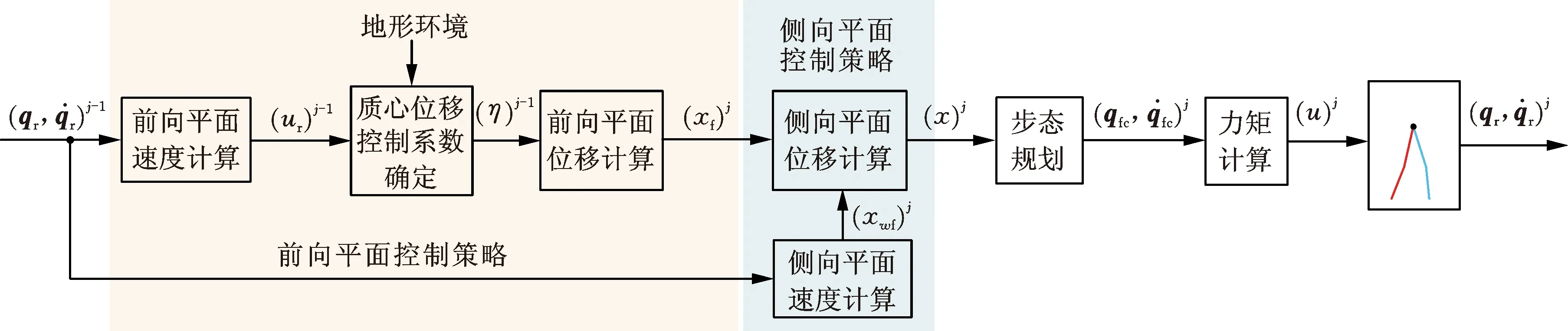
圖2 控制策略框圖

2.1 前向平面控制算法

觀察人類步行姿態發現，通過調整身體姿態可實現步行速度控制：身體前傾，步行速度增加；身體后仰，步行速度降低。人類在不平地面上步行時，將根據地形變化進一步調整身體姿態，實現步行速度控制。因此，筆者提出一種基于質心運動狀態的欠驅動步行控制策略，實現機器人在不平地面上穩定步行。選擇步行單足相終止時刻質心水平速度uf為控制輸出，單足相終止時刻質心與支撐足相對位置的水平分量xf為控制輸入，機器人步行系統被簡化為一個單輸入-單輸出系統。控制策略通過調整xf實現uf的控制，進而實現機器人穩定行走。

雙足機器人在不平地面上行走時，由于地面不平整，導致其足部落地點不在同一平面上,因此，可根據足部落地點將不平地面等效為不同傾斜角度的斜坡，如圖3所示，其中，γi為對應不平地面的等效斜坡傾角。為確定xf與uf的映射關系，將“機器人-地面”模型等效為“桿-地面”模型。根據機器人步行單雙足相，等效的“桿-地面”模型可分為碰撞子模型和擺動子模型；為確定兩個子模型的切換時間，使用“桿-地面”接觸點處水平速度衰減率λ來判斷。在t1時刻，當機器人足部-地面接觸點處水平速度衰減率為λ時，等效模型由碰撞子模型轉換為擺動子模型。

圖3 不平地面上等效運動模型

碰撞子模型的求解分為以下兩個步驟：

(1)假設桿僅受水平方向地面作用力，然后使用中值定理對桿的狀態進行修正。僅受水平方向作用力時，碰撞終止時刻桿質心狀態方程為

(11)

(12)

(2)增加豎直方向地面反力修正質心狀態，得到碰撞終止時刻桿質心狀態方程:

(13)

在擺動子模型中，使用倒立擺來描述桿運動狀態。為便于分析，將倒立擺質心運動軌跡簡化為一條直線，如圖3c所示。得到等效擺動子模型中質心能量變化:

(14)

式中，θi、θf分別為擺動的始末狀態角。

綜合以上各式，得到一個完整步行周期內等效模型質心能量變化：

E=Kf+ΔW

(15)

Kf=mtol(u2+v2+ρ2ω2)/2

經過一個完整步行周期后，桿質心的水平速度為

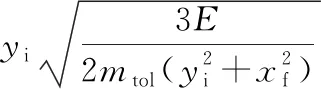
(16)

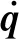
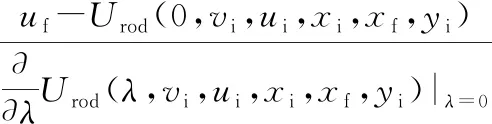
(17)

設機器人步長為Lstepd，使用ufd作為已被證明可維持機器人穩定步行的質心速度[16,18]，則在x=xi處使用一階線性化，得到下一步行周期質心位移xfc:

xfc=χ(λ,η,vf,uf,xi,yf,Lstepd,ufd)=xf+ηΔxf=

(18)

其中，η為與不平地面等效斜坡傾角γi相關的質心位移調整系數。由圖3可知，當γi>0時，地面高度增加；γi<0時，地面高度降低，本文的等效斜坡傾角在[-10°,10°]范圍內。當機器人在不平地面上行走時，控制器首先根據測量得到的地形數據計算等效斜坡傾角γi，然后根據γi對參數η進行調整，最后利用式(18)得到調整后的質心位移xfc，實現質心速度uf對理想速度ufd的跟蹤，進而實現機器人穩定步行。

由于本文所提控制策略需要根據下一步行周期地形變化計算等效斜坡傾角，故步行環境需要已知。但與其他已知環境的步行控制策略不同，本文控制策略無需已知整個環境的地形變化，僅需已知下一步行周期地形變化即可，適用于實際機器人步行系統。

2.2 側向平面控制算法

三維行走失穩的主要原因是側向運動與前向運動不匹配，故可利用“桿-地面”模型等效機器人側向運動模型，通過控制質心側向速度對前向速度進行跟蹤，保證側向運動與前向運動相匹配，實現三維欠驅動穩定行走。

當只考慮機器人側向運動時，步行類似原地踏步，為降低研究難度，規定側向運動過程中軀干豎直、髖部保持水平，且忽略前向運動導致的腿長變化。機器人側向運動過程如圖4所示，圖4a～圖4d所示的4種姿態分別記為A、B、C、D，其中A表示機器人由左腿支撐轉換為右腿支撐，B表示左腿支撐機器人運動最大姿態，C表示機器人由右腿支撐轉換為左腿支撐，D表示右腿支撐機器人運動最大姿態，狀態A-B-C為左腿支撐階段，狀態C-D-A為右腿支撐階段。

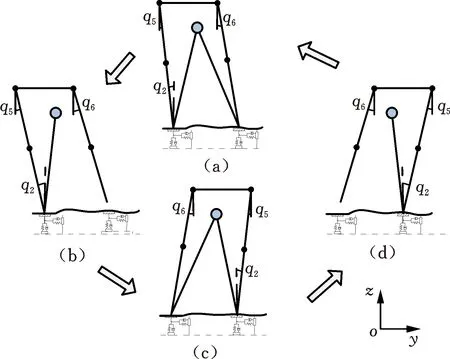
圖4 機器人側向平面運動過程

使用三維線性倒立擺模型描述機器人側向運動，由其動力學方程可知，等效線性倒立擺的軌道能量為

(19)

其中，x為前向平面質心位移，y為側向平面質心位移；Ex、Ey分別為前向平面與側向平面軌道能量。則質心在水平面上投影軌跡方程為

(20)

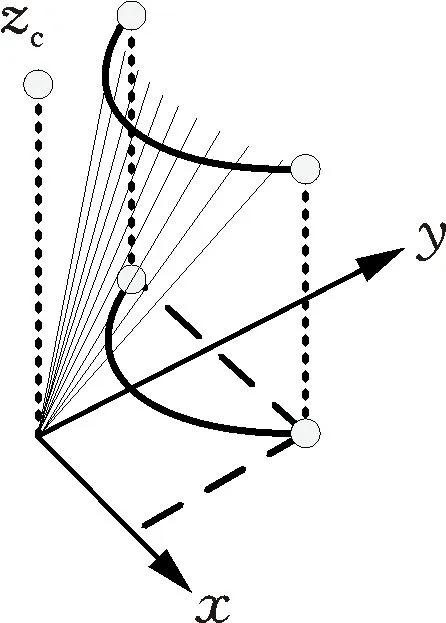
(a) 機器人等效三維線性倒擺模型

由于桿質心前向和側向位移關系可用雙曲線表示，為降低計算量及增加求解速度，本文使用四次多項式對質心軌跡進行擬合，得到質心側向軌跡方程：

y=a0+a1x+a2x2+a3x3+a4x4

(21)

根據質心在步行初始及終止時刻位移、速度，運動過程中最大擺幅，可確定式(21)中多項式系數a0～a4。

綜上，通過控制質心側向運動對前向運動的跟蹤，保證兩者相匹配，可實現雙足機器人欠驅動穩定行走。

3 試驗與分析

3.1 物理樣機

為驗證所提控制策略的有效性，設計欠驅動雙足機器人樣機如圖6所示，圖6中，①為機器人主控器。機器人具有8個主動自由度：左右腿髖關節各2個自由度(圖6中②)、膝關節各1 個自由度(圖6中③)、踝關節各1個自由度(圖6中④)。機器人采用弧狀足部設計，忽略足部防滑橡膠皮墊微小變形，步行過程中足部與地面始終保持線接觸。步行單足相階段，足部與地面間無驅動，步行處于欠驅動狀態。機器人還配備有移動保護架，當機器人出現不穩定狀態時，可對其進行保護。機器人總質量為29.5 kg，高度為743 mm，各部分詳細參數見表1。

圖6 機器人樣機

表1 機器人主要參數

根據表1中機器人參數，在MATLAB中仿真得到一組步長為0.1839m的可維持機器人穩定步行的步態：

qfs=(0.3062,0,0.0661,0.2401,0,0,-0.2382，-0.5459)T

0.7885，3.2917)T

3.2 仿真試驗

在進行仿真試驗前，需確定不同等效斜坡傾角γi對應的質心位移調整系數η。本文通過仿真試驗與差值擬合來確定η的取值，首先選擇幾個固定傾角作為測試對象，確定可維持機器人穩定行走的η取值范圍；然后根據質心速度的最大超調量和調整時間優化η取值；最后使用多項式插值確定不同等效斜坡傾角的η值。

以剛度系數k=24×104N/m、阻尼系數c=32×105N·s/m作為地面柔性參數，將本文研究的等效斜坡范圍[-10°,10°]平均分為40份，對機器人步行前100周期進行分析。定義NΔ=5為機器人質心水平速度達到穩態誤差5%內所需調整周期數，MP為質心速度的最大超調量，Γi為目標函數，Γi最小值對應η最優值。有

(22)

以等效斜坡傾角為6°時為例，記錄機器人在η取不同值時對應質心水平速度的變化情況，如圖7所示。由圖7可知，η值在(0,0.5]內，機器人質心水平速度可以收斂，η最優值為0.35。

圖7 等效斜坡傾角為6°時uf變化情況

同理，得到等效斜坡傾角在[-10°,10°]內機器人可維持步行的η可取值和最優值，如圖8所示。其中，藍色區域為η可取值，紅色星號點為測試點處η最優值，粉色曲線為擬合得到的[-10°,10°]范圍內η最優值。

圖8 η取值范圍與最優值

確定不同等效斜坡傾角γi對應的質心位移調整系數η后，進行仿真試驗。試驗隨機生成3組不平地面環境，機器人在每組環境中需完成30周期步行，計算不平地面的等效斜坡傾角，如圖9a所示，其中，傾角范圍均在[-10°,10°]內。分別使用本文提出控制策略與已有的混合零動態(hybrid zero dynamic, HZD)[19]方法進行仿真試驗，驗證所提控制策略的有效性。記錄3次試驗過程中步行單足相終止時刻，2種控制器作用下前向和側向平面質心水平速度uf和wf的變化趨勢，如圖9b、圖9c所示。由試驗結果可知：

(1)在混合零動態方法作用下，機器人無法完成不平地面上步行試驗，3次試驗分別完成了7、11、10周期步行后，uf和wf發散，機器人失穩。

(2)在本文所提出控制策略的作用下，uf和wf均可穩定在一定范圍(uf處于0.4～1.5 m/s區間內，wf處于0.1～0.9 m/s區間內)內，與所提欠驅動步行穩定判據相符，實現了機器人在不平地面上的穩定步行。

(a) 三組工況下不平地面對應等效斜坡傾角

3.3 樣機試驗

使用本文所提控制策略與混合零動態方法進行樣機試驗，記錄不平地面上機器人步行過程，如圖10所示：首先，機器人在木地板上完成3個周期平地步行后，左腿支撐右腿邁上PVC橡膠地板，如圖10a～圖10d所示；其次，右腿支撐，左腿邁上PVC橡膠地板，如圖10e～圖10h所示；然后左腿支撐右腿擺動，平地步行1個周期后，右腿支撐左腿邁下木地板，如圖10i～圖10l所示；最后，左腿支撐右腿擺動，平地步行1 個周期后，機器人邁下PVC橡膠地板。

(a) DSP

記錄2種控制器作用下，3次步行試驗過程中單足相終止時刻，前向和側向平面質心水平速度uf和wf變化趨勢，如圖11所示。由試驗結果可知：

(1)在混合零動態方法作用下，機器人無法實現不平地面上穩定步行，3次試驗分別完成了4、5、4周期步行后，機器人失穩。

(2)本文所提控制策略可適應地面材質和地形的變化，實現機器人在不平地面上穩定步行。控制器從第3周期開始工作，uf下降趨勢得到抑制，但由于地面高度增加，uf出現衰減，且3次試驗uf平均衰減量為0.058 m/s。

(3)機器人邁向木地板時，由于地面高度變化較小(高度差為5 mm)，故質心速度波動不明顯；邁向PVC橡膠時(高度差為15 mm)，地面高度變化較大，uf顯著提高，3次試驗uf平均增量為0.0423 m/s。之后為抑制uf增大，控制器減小質心位移輸出，證明所提控制器可抑制地形變化對質心速度產生的影響。

(a) 前向平面質心水平速度uf變化趨勢

4 結論

(1)使用“彈簧-阻尼”系統建立“機器人足部-地面”柔性接觸模型，采用解耦建模的方式建立了“機器人-地面”耦合動力學模型。

(2)通過觀察人類步行特征，提出一種基于質心運動狀態的欠驅動步行控制策略，將三維欠驅動步行解耦為前向和側向的主從控制，通過控制質心速度實現機器人穩定步行。

(3)通過與已有的混合零動態方法進行對比試驗，證明了本文所提控制策略的有效性。

本文實現了不平地面上欠驅動步行，但不平地面的起伏較小，如何對控制策略進行改進，使其適用于地面起伏更大的環境，是下一步研究的主要方向。