兼容bfloat16 的高速浮點加法器設計

胥 濤， 秦水介， 鄧 全

（1 貴州大學 貴州省光電子技術及應用重點實驗室， 貴陽 550025； 2 國防科技大學 計算機學院， 長沙 410073；3 貴州大學 大數據與信息工程學院， 貴陽 550025）

0 引 言

隨著信息時代的到來，圖像識別、深度學習、數字信號處理和人工智能等應用技術在不斷地發展，需要處理的數據量正與日俱增，對于計算能力的要求也越來越高。 由于浮點數科學計數的方式，在圖像識別、機器學習等領域得到了越來越廣泛的使用，對于數據計算速率的提升有很大的作用。 由于浮點的加法、減法、轉換、比較都可以轉換為加法或者復用加法的部分計算來實現，使得浮點加法在運算中使用頻率占50%以上［1］，所以浮點加法的性能提升對于浮點計算能力的提高有著非常重要的意義。

在機器學習等領域發展過程中發現，一般情況下不需要用到32 位和64 位的高精度數據，而bfloat16 的數據格式比IEEE 754-2008 定義的16 位數據表示范圍更大，對比32 位和64 位數據而言，尾數較小、精度較低在計算時容易在舍入上出現錯誤；而精度低也表示在相同內存下，bfloat 格式可以存放更多數據，數據的存取移動速度更快，同時在計算部件的實現上也會更加簡單。

bfloat16 格式是指1 位符號位、8 位階碼、7 位尾數組成的浮點數，形式上相當于單精度浮點數的高16 位；同時相比IEEE 半精度浮點階碼更大，尾數更小，可以發現就能在降低精度的情況下表示更大范圍的數據。 由此有一些處理器已經將bfloat16 數據的計算加入設計規劃，比如ARM 宣布將bfloat16 數據格式加入下一版本的Armv8-A 架構［2］。

現在主流的浮點計算還沒有實現兼容bfloat16數據的相關計算，為了滿足對浮點計算速率更高的要求，本文提出一種支持bfloat16 的高性能浮點加法器設計，包含設計要點，性能報告等。 本文工作包括算法修改、縮拍設計、bfloat16 計算兼容。 其中，算法修改是為了更好地實現縮拍設計，在原來的3 拍流水線設計上，各拍計算功能分配合理，頻率相對較高，但絕對延時為3 拍。 為了滿足2 拍流水線的設計，優化后的算法將前導零預測和尾數計算改為并行計算，減少了整體的計算時間，將絕對延時減為2拍，但是每拍的計算操作更多，功率更高。 算法修改后將流水線縮減為2 拍可以盡可能避免頻率減小。

實驗數據表明，最終設計相比原始設計頻率下降1.36%，達到2.16 GHz，面積增加14.01%，功率增加53.31%，為2.181 1 mw。

1 高性能浮點加法器設計

浮點加法算法主要可以分為單通道計算算法、雙通道計算算法、三通道計算算法等，主流為雙通道算法（Two-Path）和三通道算法（Triple-data-path）。

浮點加法計算過程簡單，分為階碼相減、對階操作、前導零預測、尾數相加、規格化舍入等運算步驟，如圖1 所示。

圖1 浮點加法流程Fig.1 Floating-point addition flow chart

1.1 3 拍流水線加法器設計結構

本設計是基于主流的TWO-PATH 算法上做出的改進，原始的加法器算法設計的是一個3 級流水線的加法器部件，簡單的算法流程圖如圖2 所示。 原始算法按TWO-PATH 結構設計，第一步是數據的預取：首先按照輸入信號的變化分辨操作數的精度，依據不同的浮點精度選取不同長度的階碼、尾數部分，對2 個操作數進行階碼相減分辨操作數的計算符合near 和far中哪一條路徑。 對于TWO-PATH 算法依據浮點加法的計算方式將加法分為near path 和far path 兩條路徑，兩者以階碼的差值相區別，當階碼的差值小于等于1時，加法對應near path 部分結果，當階碼差值大于1時，加法結果為far path 路徑結果。

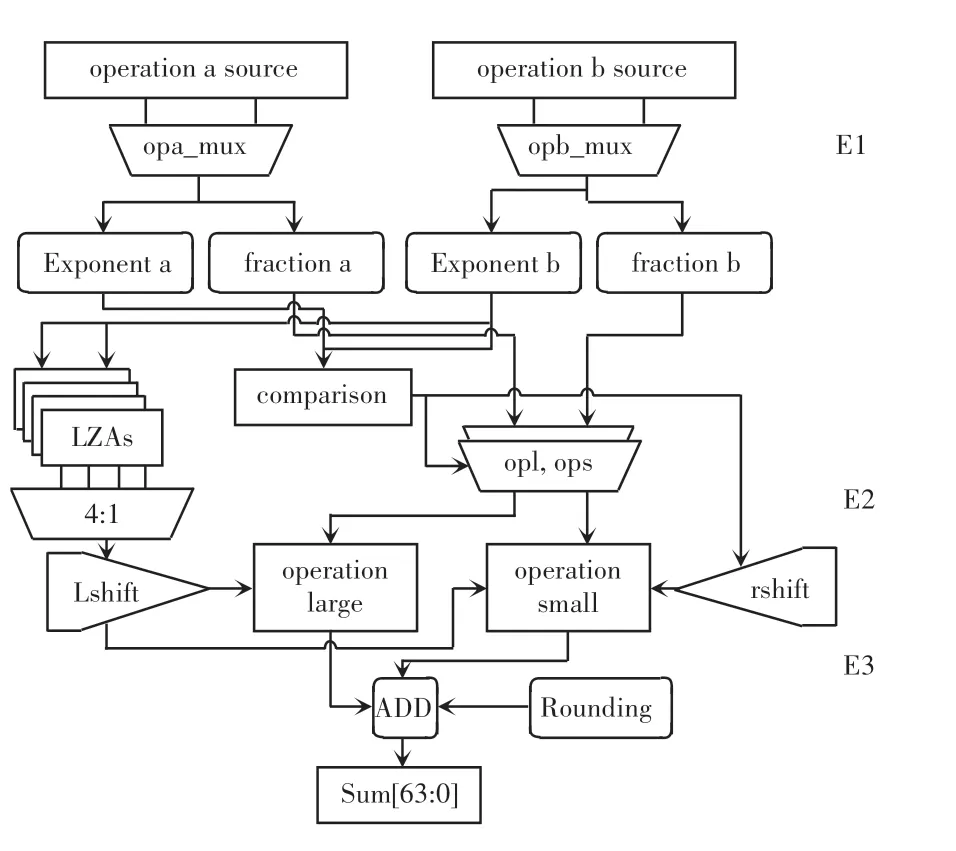
圖2 浮點加法3 級流水線示意圖Fig.2 Schematic diagram of the three-stage pipeline for floatingpoint addition

第二拍的操作是將near path 路徑數據的尾數部分進行前導零預測計算，計算前需將數據右移一位的同時在最高位補1，這是由于規格化浮點數的尾數部分總是默認舍棄最高位1，在計算過程中還要回復原始數據計算。 根據操作數階碼的差值和尾數的大小比較確定右移的位數，判斷操作數的大小。根據小數靠大數的原則右移尾數部分，然后根據前導零預測的數據左移操作數尾數部分，最后進行尾數的加法操作。

第三拍的計算操作是舍入和數據選擇，根據計算指令規定的舍入模式對加法的結果進行數據舍入，同時根據浮點計算的規則和操作數的情況，分辨結果是near path 路徑結果、還是far path 路徑結果、或者是特殊值。

1.2 優化的浮點加法器設計結構

優化算法的結構也是基于TWO-PATH 的算法，其中對于關鍵路徑的時序進行了優化，將計算過程的絕對延遲縮減到2 拍，且支持流水線操作。

浮點加法3 級流水線的設計見圖2，本文提出加法計算結構將計算的步驟縮減到2 拍，即：E1 和E2。 在初始算法設計3 拍流水線的基礎上，為了提高計算速度，降低流水線拍數，在第一拍完成數據分解和計算階碼差值后，將較小操作數尾數部分對階的右移操作也放到第一拍，加快near path 路徑計算；在第二拍完成尾數部分的補碼加法，計算尾數部分的前導零預測的結果，取消對操作數規格化的操作，改為對結果進行規格化，然后對結果進行舍入計算，減少了near path 的計算時間。

原始算法的加法設計在劃分流水線時，將數據的右移對階部分、前導零預測部分、左移規格化部分都設定在同一拍的流水上，由于前導零預測的復雜性，大大占用了節拍時間。 為此在新設計中，為了在縮拍后避免時序的沖突，將階碼對階定制在第一拍的計算中，將前導零預測和計算排定在第二拍中，看起來似乎加大了第二拍的運算時間，然而對于整體計算過程而言，原設計在尾數相加之前的對階操作、前導零預測和規格化左移是一個連貫有序的過程，后續的規格化左移只能等待前兩者完成后才能啟動；而對于新設計而言，在上一拍已經進行了對階右移操作，而規格化左移的計算是針對結果去做的，這并不會影響正常的尾數加法，所以前導零預測和尾數的相加并行進行，如此則縮短了整體的計算時間。 綜上縮拍的結果符合設計的要求，在保證頻率的情況下減小整個加法的計算時間，完成了流水線縮拍設計。

在此基礎上，根據TWO-PATH 算法的規則，分別選取符合far path 和near path 的數據建立測試功能點，對于特殊數如：無窮大（inf）、NaN（not a number）等也考慮在內，接下來基于這些功能點編寫定向測試激勵測試功能完整性。

在做縮拍設計時，會遇到的較為典型的信號傳導和時序匹配問題，比如功能驗證時發現階碼計算出錯的問題，排查發現是階碼信號傳遞的判定信號和前導零預測結果的傳遞判斷信號相同，但是兩者在計算時是一個串行的關系，所以出現計算錯誤。這是在節拍控制上對于相關問題考慮上發生的疏漏所致。 所以需要考慮到數據傳遞和計算在時序分配上的關系，從而避免設計沖突。

1.3 兼容bfloat16 的設計

1.3.1 設計結構

本設計將bfloat16 格式的計算放在16 位浮點加法模塊中，如果將bfloat16 浮點數看做32 位IEEE標準數據的前半部分計算，將其和32 位單精度加法結合，那么實現起來會很簡單，對于設計的改變較小；但是這樣設計考慮到精度混合計算時，在一個64 位雙精度計算部件中只能兼容2 個32 位單精度計算、或2 個bfloat16 計算、或4 個半精度計算；所以研究中將其與IEEE 格式的16 位半精度加法計算結合在一塊，這樣一來64 位雙精度計算部件可以兼容2 個32 位計算、或4 個bfloat16 計算、或4 個半精度計算，利用計算部件的復用實現兼容bfloat16 格式，減小資源的消耗，兼容bfloat16 的半精度加法的設計如圖3 所示。

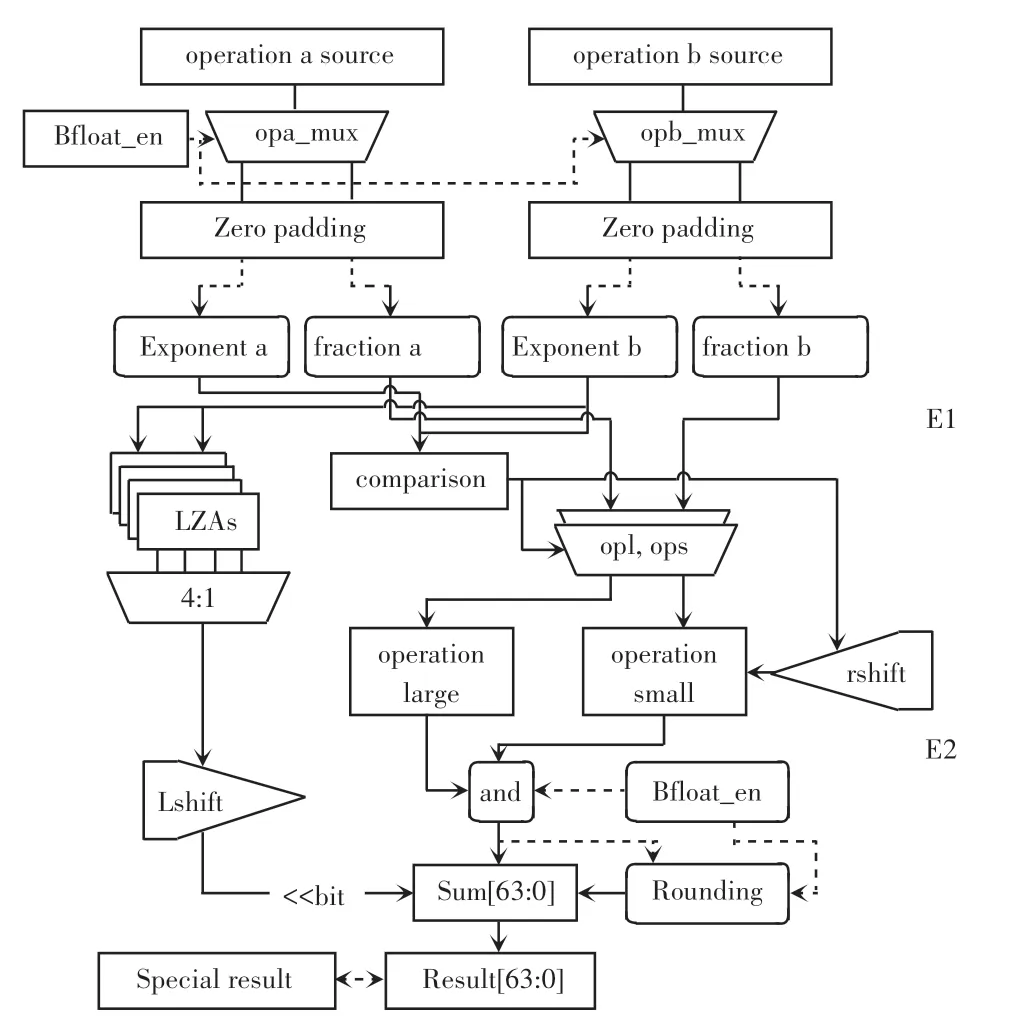
圖3 兼容bfloat16 的半精度加法Fig.3 Half-precision addition compatible with bfloat16

對于半精度的數據而言只有5 位的階碼長度，所以要達到兼容bfloat16 的情況要擴展高位，為了不影響正常的半精度階碼計算需要在高位補0，而尾數的計算，為了保證bfloat16 數據計算的正確性，需要在數據分解時，將尾數部分放在高位，在低位補0。 為了區分計算需要添加bfloat 使能信號，在前導零預測中bfloat16 最多可移動位數是7，小于半精度的10 位，所以前導零預測的部件復用對于結果不會產生影響。 在舍入計算中同樣需要區分兩者的不同有效部分，由于舍入的判定都是由有效位后的數據和舍入模式決定的，計算結果選取也要選擇相應的有效位數，這些都需要考慮bfloat16 和半精度浮點的區別。

設計工作要考慮bfloat16 數據和正常浮點數的計算差別，包括數據格式、特殊數選取、舍入模式等方面。 基于浮點計算的共通之處則要盡可能復用正常浮點的計算通路減小功耗。

在進行了兼容bfloat16 計算的設計后，先利用寫好的定向測試激勵驗證正常浮點數計算功能是否破壞，再根據TWO-PATH 算法和bfloat16 的數據格式建立功能點，重新編寫定向激勵測試設計的功能是否成功。

1.3.2 bfloat16 對于特殊數的處理

對于無窮大、NaN 數、subnormal 數的格式和IEEE 標準類似，只是數據的位數不一致。 其中，無窮大數和NaN 數都是階碼為全1，尾數為全0 和不為全0 的數；subnormal 數是階碼為0，尾數不為全0的數；subnormal 數階碼為0，但表示的數據階碼在計算時等同于1。

對于這些特殊數據在計算時的處理使用的RISC-V 的處理情況，正負零相加減，結果為正零；若符號位相同，則符號位取任意操作數符號位。NaN 數與任意數據相加減結果為canonical-NaN，兩NaN 數相加減結果也為canonical-NaN；正無窮大加減數據結果為正無窮大，負無窮加減結果為負無窮，正負無窮相加減結果為canonical-NaN。

對于這些特殊數據的計算，為了實現特殊結果的輸出，在數據輸入后就會進行特殊數的判斷，比較階碼和尾數部分是否全為1、或全為0，從而判斷是哪一種特殊情況，根據設計規則輸出標準結果。

2 實驗

2.1 實驗環境

利用核級環境調用加減法指令測試實驗功能準確性，利用DC 綜合工具進行綜合仿真。 實驗分為設計修改、定向測試激勵驗證、EDA 軟件綜合PPA對比。

分析可知，驗證即是芯片設計過程中值得關注的重要問題，隨著芯片功能的不斷強大，驗證環境涉及的各類情況越發復雜，需要占據設計環節越來越多的時間和工作。 本設計只需要驗證BF 浮點16位加法功能的正確性，只使用定向測試激勵驗證設計功能。 簡單來說，設計對應的bfloat16 的計算數據，準備正確結果作為比對值，在計算結束后將計算結果與預設值比較，這些過程都由匯編指令完成。

對于本設計的驗證，選擇了利用浮點指令的定向激勵做測試，定向測試激勵都利用risc-v 支持的匯編指令編寫，整個過程具體分為：調用訪存指令讀取數據、利用浮點搬運指令放入浮點寄存器、調用浮點加減指令、計算結果寫回寄存器、寫入正確結果對比值、調用比較指令、輸出比較結果。 數據選取考慮到了正常的數據計算（包括near path 和far path 的各樣需要移位的情形）、非特殊數的臨界數據計算、無窮大和NaN 數等特殊數的計算情形。

本設計使用的EDA 軟件綜合工具來對設計進行綜合驗證，使用軟件綜合的結果可得到較為優化的時序效果，會自動對設計中部分參數進行優化，比如設計尺寸、電路拓撲結果、時序約束等，所以EDA的軟件綜合結果比其他工具在面積、速度上更加精簡。 實驗比較了原始算法、縮拍新算法設計、兼容bfloat16 算法三種設計。

2.2 實驗結果

EDA 綜合數據符合預期。 原始算法、改進算法和兼容bfloat16 格式的EDA 綜合數據見表1。

表1 EDA 綜合結果Tab.1 Comprehensive results of EDA

表1 中，數據前四列為EDA 工具綜合出的4 個路徑組，對應的數據為該路徑的slack 值；后三列為設計占用的硬件資源。 slack 值代表的數據為設計要求時間和dc 工具模擬出的時間的差值：當slack為正數，表示在要求時間內可以完成該路徑計算；為負值，表示計算時間超過約束值。 本設計中使用的約束時間為0.455 ns，原始算法恰好滿足結果，其頻率達到2.2 GHz；對于改進算法，由于進行了拍數縮減，使得在盡量保持頻率的情況下減少了硬件計算資源，其頻率達到2.16 GHz；兼容bfloat16 計算的算法，在設計實現下其頻率為2.17 GHz，與原算法相比在縮減流水線兼容bfloat16 計算的情況下其頻率下降1.36%，面積增加14.01%，功率增加53.31%。

定向測試激勵測試結果：bfloat16 浮點加法減法計算，特殊數計算結果均符合預期，正常IEEE 標準浮點計算結果正常。

3 結束語

本設計提出一種兼容bfloat16 格式的高速浮點加法設計，在保證正常的16、32、64 位浮點計算的同時將執行流水線縮減至2 拍，頻率可達2.17 GHz，功耗為2.181 1 mw。本設計可以保證在深度學習、圖像識別等領域進行計算時使用bfloat 格式浮點數計算，提高計算速度；但由于是在原浮點加法部件上進行的兼容設計，整個計算的功能變得龐大，雖然做了流水線縮拍設計，但整個部件的頻率還是有略微下降，并且功耗加大，所以還需進一步改善設計的功耗面積等相關方面。