基于神經網絡的集裝箱船港口作業時間預測模型
韓宗壘 徐 斌 陳 佳
(大連海事大學遼寧省物流航運管理系統工程重點實驗室 遼寧 大連 116026)
0 引 言
泊位是港口的重要資源,合理的泊位計劃能有效提高港口生產效率,減少船舶在港時間,從而提高港口的競爭力。Imai等[1]釆用連續區位空間的方法對連續型泊位計劃進行研究,建立了船舶等待時間和作業時間最小的數學模型并采用拉格朗日松馳系數算法進行求解。張煜等[2]考慮在泊位計劃中岸橋的分配影響集裝箱船的裝卸作業效率,依據規則建立確定船舶集裝箱裝卸作業時間和分配岸邊起重機的算法。秦進等[3]提出基于時間窗約束的離散型泊位計劃模型,建立了模擬退火算法模型進行優化求解。韓曉龍等[4]在港口船舶的目標函數中加入了船舶作業時間,對船舶的服務時間和作業時間提出了時間窗約束,建立了以最小化卸船完工時間為優化目標的混合整數規劃模型和約束規劃模型。曾慶成等[5]用船舶裝卸集裝箱量除以岸橋裝卸效率來預測集裝箱船港口作業時間。
綜上所述,大量的研究表明集裝箱船港口作業時間對于制作科學高效的泊位計劃是非常重要的,研究中用的是傳統裝卸集裝箱量除以岸橋裝卸效率的預測方法,預測精度較低,因此尋找一種科學的方法來預測集裝箱船港口作業時間是非常有意義的。本文基于神經網絡針對集裝箱船港口作業時間預測的問題建立模型,通過與傳統預測方法的對比驗證了模型的可行性。
1 問題描述
在集裝箱船實際到達港口之前,港口需要根據船期表制作泊位計劃確定集裝箱船靠泊的時間和位置。集裝箱船港口作業時間(船舶開始裝卸第一個集裝箱到完成裝卸最后一個集裝箱的這段時間)是制作泊位計劃的主要依據,而集裝箱船港口作業時間的主要獲取方法是預測,所以預測出精確的集裝箱船港口作業時間可以提高泊位計劃的效率。
傳統的集裝箱船港口作業時間預測方法是船舶待裝卸的集裝箱量除以岸橋的裝卸效率。這種預測方法不靈活并且預測精度較低,集裝箱船港口作業時間受多種因素的影響[6],如船舶類型、岸橋數、裝卸集裝箱量、天氣等,并且存在復雜的非線性關系。考慮到集裝箱船港口作業時間與影響因素之間復雜的非線性關系,本文選取了比較適用的BP神經網絡建立集裝箱船港口作業時間預測模型。模型的目標是預測出更加精確的集裝箱船港口作業時間,從而保證制作的泊位計劃更加科學高效。
2 模型建立
BP(Back Propagation)神經網絡是一種多層前饋神經網絡,由輸入層、隱含層、輸出層組成,可以以任意的精確度逼近任意一個連續的函數,所以經常被用于非線性建模、函數逼近和模式分類等方面。BP神經網絡的主要特點:信號是前向傳播的,誤差是反向傳播的。
2.1 網絡的層數
1989年Robert Hecht-Nielson證明了對于任何一個閉區間內的函數,都可以用有一個隱含層的BP神經網絡來逼近,所以一個三層(含一個隱含層)的BP神經網絡可以完成任意的n維向m維的映射。在多數的實際應用中一般都取三層的BP神經網絡來解決問題,所以本模型選取了三層的神經網絡。
2.2 輸入和輸出層神經元個數
BP神經網絡的輸入和輸出層的神經元個數完全根據使用者的要求進行設計。影響船舶港口作業時間的因素有很多,通過分析確定了船舶類型、岸橋數量、卸20尺箱量、裝20尺箱量、卸40尺箱量、裝40尺箱量、卸特種箱量、裝特種箱量和天氣作為模型的輸入。本模型根據輸入樣本的維度,將輸入層設置為9個神經元。集裝箱船港口作業時間預測模型最后輸出的是集裝箱船港口作業時間,所以輸出層神經元的個數為1。
2.3 隱含層神經元個數
隱含層對于整個神經網絡的精度起著至關重要的作用,隱含層神經元個數的選取與輸入、輸出層神經元個數都有直接的關系。神經網絡精度的提高可以通過增加隱含層神經元的個數來實現,隱含層神經元的個數較少時,神經網絡就不能較好地學習,導致模型不能較好地擬合數據,訓練精度和預測精度都不高,出現欠擬合的情況;隱含層神經元個數較多時,模型結構可能過于復雜,導致過度的擬合訓練數據,而對測試數據的預測能力較差,出現過擬合的情況,所以選取準確的隱含層神經元個數是很重要的。隱含層神經元個數選取的方法很多,結合開發的神經網絡生成器,本模型采用式(1)選取隱含層神經元個數[7]。
(1)
式中:p為隱含層神經元個數;n為輸入層神經元個數;m為輸出層神經元個數;a為1~10之間的常數。經過試算最終確定隱含層神經元個數為10。
2.4 激活函數
BP神經網絡的激活函數有多種。其中Sigmoid函數對于網絡不同輸入,將其輸出范圍控制在(0,1)之間,公式如下:
(2)
Tanh(雙曲正切)激活函數對于不同范圍的輸入,將其輸出值范圍控制在(-1,1)之間,公式如下:
(3)
線性激活函數Purelin的輸入與輸出值可取任意值,公式如下:
f(x)=x
(4)
本模型選取Sigmoid作為隱含層的激活函數,Purelin作為輸出層的激活函數。
2.5 LM-BP算法
標準BP算法是根據梯度下降法來調整權值的:
Δw=-ηg
(5)
式中:Δw為權值閾值更新量;η為學習速率;g為梯度。
權值沿著與誤差相反的方向移動,使得誤差函數減小,缺點是神經網絡收斂較慢,且學習速率不容易被確定。LM(Levenberg Marquardt)算法是一種利用標準的數值優化技術的快速算法,是梯度下降法和高斯-牛頓法的結合,既有高斯-牛頓法的局部收斂性,又有梯度下降法的全局特性,具有收斂速度快、魯棒性好的特點。下面對LM算法做簡要闡述:
設網絡的誤差函數為:
(6)
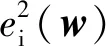
用wk表示在第k次迭代的權值和閾值,迭代完成后的權值和閾值組成的向量為wk+1,Δw是權值和閾值的改變量,則有:
wk+1=wk+Δw
(7)
牛頓法是通過最小二乘法求解誤差函數E(w):
Δw=-[▽E2(w)]-1▽E(w)
(8)
式中:▽E2(w)是誤差E(w)的Hessian矩陣,▽E(w)表示梯度,對Hessian矩陣進行近似計算,可以表明:
▽E(w)=JT(w)e(w)
(9)
▽E2(w)=JT(w)e(w)+S(w)
(10)
式中:J(w)是e(w)的Jacobian矩陣;S(w)是誤差矩陣。
在靠近極值點時S(w)≈0,牛頓法可以修正為高斯-牛頓法,經過改進得到修正權值閾值的公式:
Δw=-[JT(w)J(w)]-1J(w)e(w)
(11)
LM算法將高斯-牛頓法經過改進得到修正權值閾值的公式:
Δw=[JT(w)J(w)+μI]-1J(w)e(w)
(12)
式中:I為單位矩陣;μ為大于0的常數。
系數μ的值很小時,LM算法就近似等于高斯-牛頓法,當μ的值很大時,就近似等于梯度下降法。每迭代成功一次μ就會除以比例系數β(β>1),這樣在接近目標誤差的時候就基本與高斯-牛頓法相等,計算速度快,精確度也高,否則μ乘比例系數β,LM算法利用近似二階導數信息,比梯度下降法快得多。在實際應用中μ是一個試探性的參數,對于一個給定值,如果求得Δw能使E(w)降低,則μ降低,反之μ增加。
2.6 相關參數
(1) 權值和閾值。選取處于(-1,1)之間的隨機數作為權值和閾值的初始值。
(2) 學習速率。神經網絡權值每次的變化量都取決于學習速率的大小,如果學習速率選取較大,系統可能因此而動蕩不穩定;學習速率選取較小則收斂速度慢,訓練時間長,網絡誤差值與誤差最小值更趨近的目標無法保障。實際應用中常選取較小學習速率給系統提供穩定性保障,所以學習速率的選取區間是[0.01,0.9]。本模型選取的學習速率為0.01。
(3) 其他。最大訓練次數為1 000次,訓練要求精度為0.000 1,極小值認定次數為50,μ的初始值為0.000 01,比例系數β為10。
3 算例分析
某港口近年集裝箱船港口作業數據中包含船舶類型、分配岸橋數、裝卸集裝箱量、天氣、計劃作業時間、實際作業時間等。集裝箱船的第一代和第六代相當少,這里只考慮第二至第五代的船型。因為原始數據中船舶類型和天氣都是文字形式,所以需要對船舶類型和天氣情況進行編碼數字化。船舶類型和天氣情況編碼后的結果如表1和表2所示。
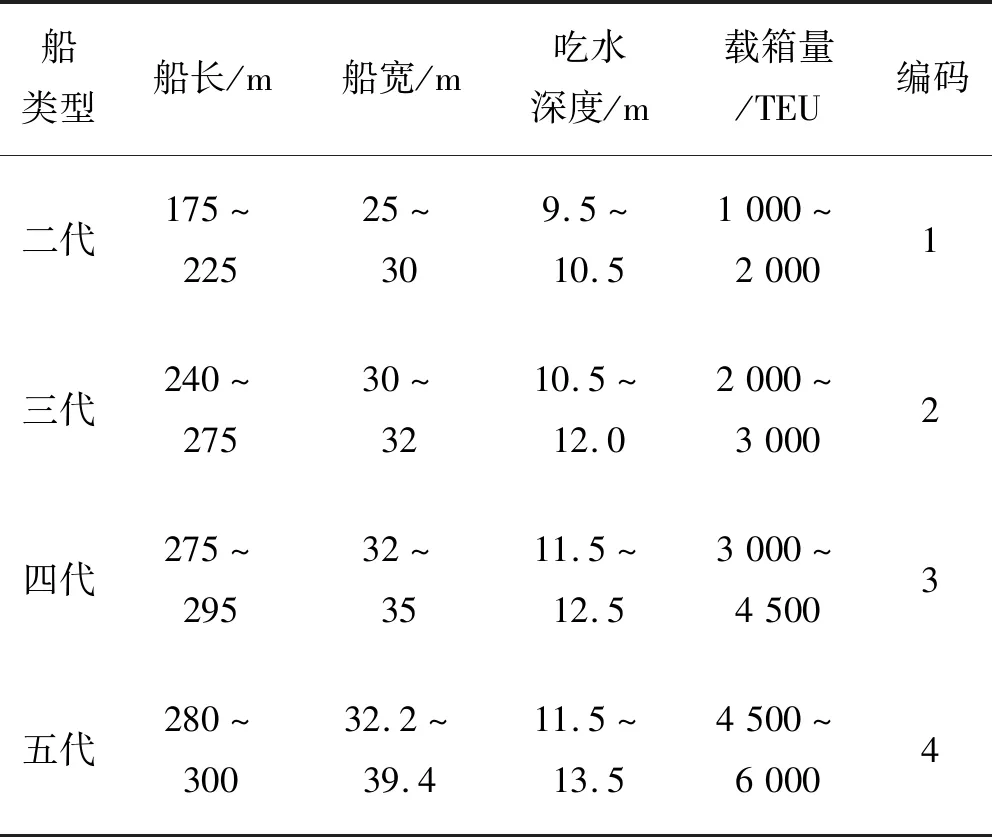
表1 編碼后的船舶類型
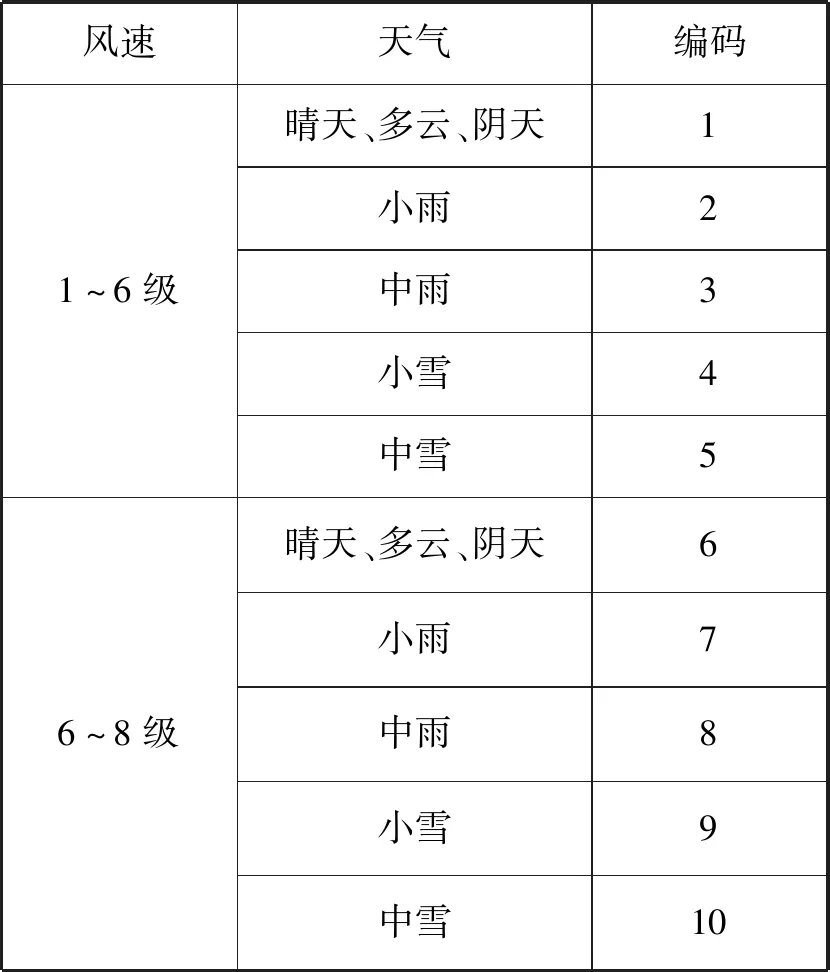
表2 編碼后的天氣
隨機選取1 000條集裝箱船港口作業信息數據作為模型的訓練集和測試集數據,由于數據量較大,這里只展示部分編碼后的數據,如表3所示。
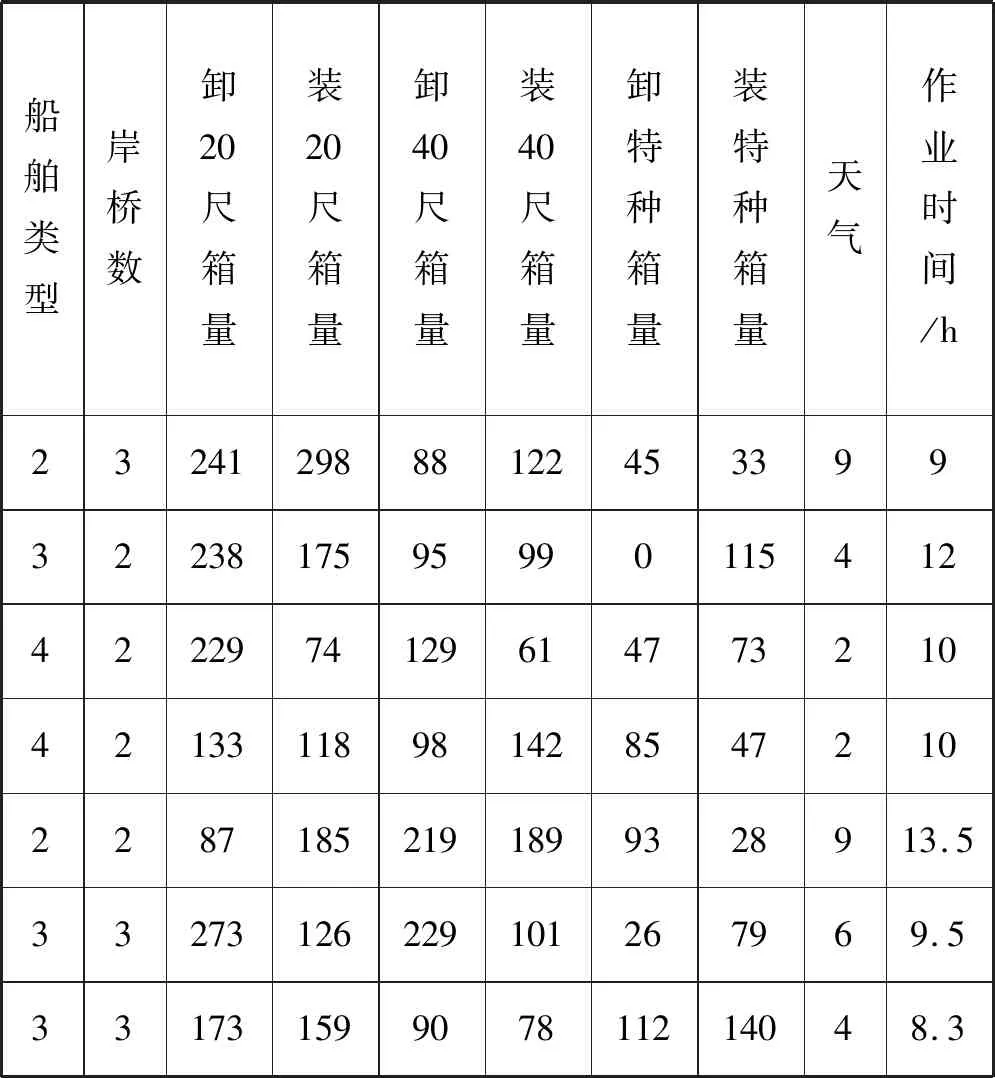
表3 編碼后的船舶信息
1) 傳統的集裝箱船裝卸集裝箱量除以岸橋裝卸效率的預測方法可以根據式(13)計算:
(13)
式中:h為集裝箱船港口作業時間;Y為裝卸集裝箱總量;v為單個岸橋裝卸效率;n為分配岸橋數。
港口單個岸橋裝卸效率為35箱/h,用傳統預測方法計算集裝箱船港口作業時間結果如表4所示。
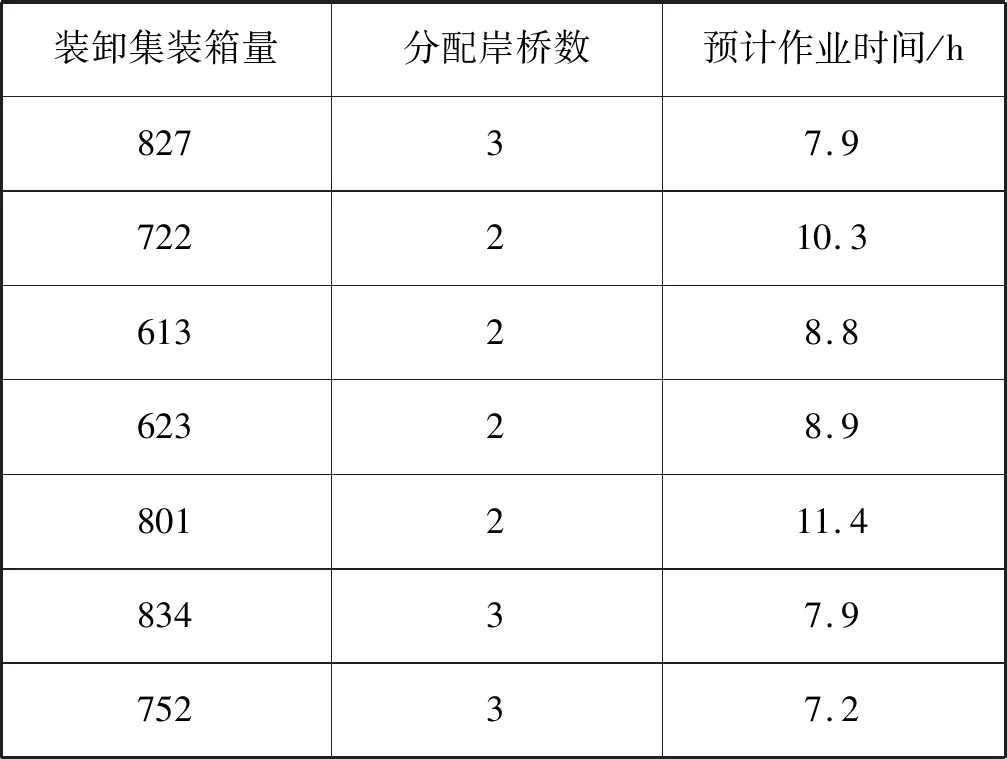
表4 傳統方法預測作業時間
2) 用神經網絡模型預測集裝箱船港口作業時間:為了消除各參數由于單位等的影響,并且樣本不一定包含極大和極小值,所以對數據用式(14)做規范化處理,使規范化后的數據范圍為 [-1,1]。
(14)
式中:y為規范化后的數值;ymax=1;ymin=-1;xmax為每一屬性中的最大值;xmin為每一屬性中的最小值;x為需要規范化的數據值。
模型訓練學習過程如下:選取樣本中的3條數據如表5所示,規范化后的樣本數據如表6所示,模型的輸入為x1,x2,…,x9,輸出為y。
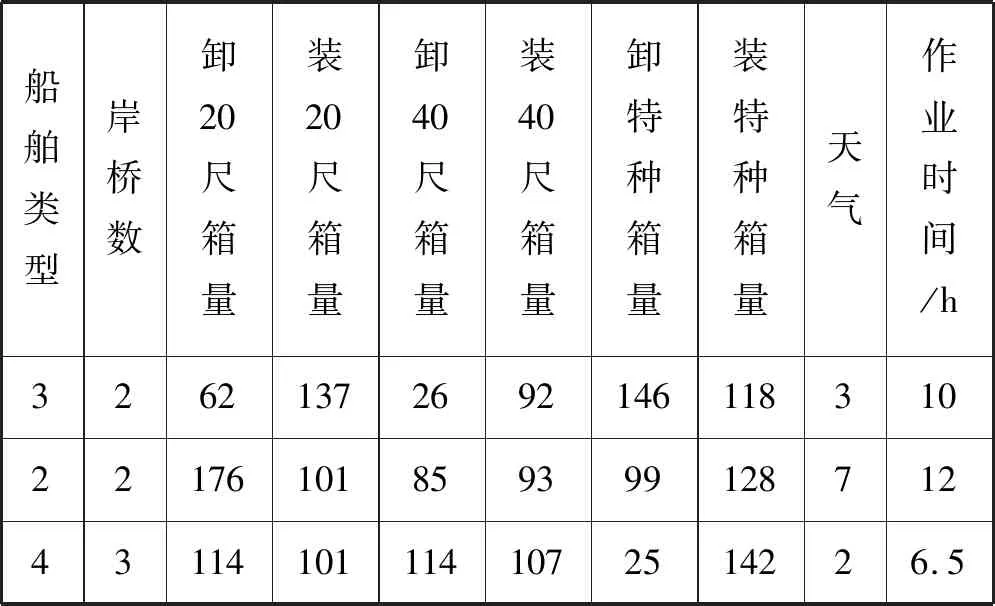
表5 樣本數據

表6 規范化后的樣本數據
(1) 設定好網絡的期望誤差值ε=0.000 1,系數β=10,μ=0.1,學習速率η=0.01,以及權值和閾值的向量:
(3) 計算Jacobian矩陣:

(4) 通過式(12)、式(6)計算出Δw:
Δw=

E(wk)=0.014 06
(5) 如果E(wk)<ε,轉到式(10),否則,用wk+1為權值和閾值計算誤差E(wk+1)=0.011 37。
wk+1=

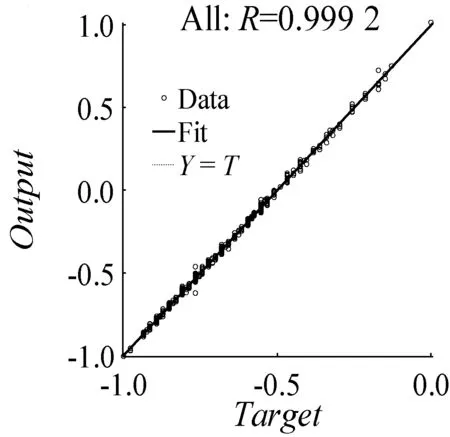
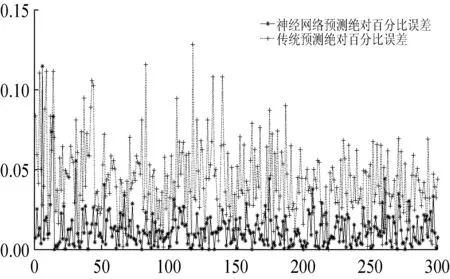
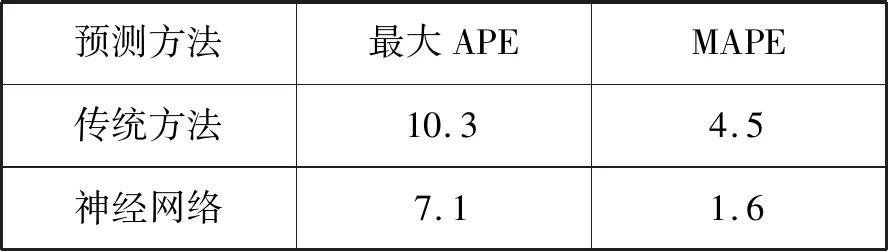
(6) 如果E(wk+1) (7) 結束。 選取數據的70%作為模型的訓練數據,數據的30%作為模型的驗證數據,運用MATLAB平臺進行集裝箱船港口作業時間預測模型實驗[8]。通過神經網絡模型的擬合效果,神經網絡模型和傳統方法預測值的絕對百分比誤差(Absolute Percentage Error,APE)、平均絕對百分比誤差(Mean Absolute Percentage Error,MAPE)的對比,評價模型的優越性。 (15) (16) 經過多次訓練學習取得最好一次結果。從圖1可以看出,隨著神經網絡迭代次數的增加,網絡的誤差逐漸變小并且趨于穩定。從神經網絡收斂效果看,當網絡訓練的次數達到87次后網絡收斂,網絡的均方誤差為0.000 27,基本達到誤差的設置要求,模型訓練效果優秀。 圖1 神經網絡迭代圖 圖2橫坐標為模型輸出的期望目標值,縱坐標為模型對數據擬合實際輸出的目標值,當模型實際輸出的值滿足在期望值上下0.001(output≈1×Target±0.001)誤差的范圍內,則說明該數據可以被模型解釋。R為被模型解釋的數據量占總數據量的比例,Fit實線表示網絡對數據訓練學習將非線性關系轉化成的線性關系,Y=T虛線代表模型擬合數據的期望線性關系。可以看出,整個網絡的數據擬合度達到99.92%,通過網絡對數據的擬合效果可以驗證該網絡模型的可行性。 圖2 神經網絡迭代圖 根據式(13)計算測試集的集裝箱船港口作業時間,根據式(15)和式(16)分別計算APE和MAPE。 通過神經網絡預測模型輸出測試集的集裝箱船港口作業時間預測值,根據式(15)和式(16)分別計算APE和MAPE。 兩種預測方法對比如下: 從圖3中可以看出,神經網絡預測集裝箱船港口作業時間的APE均明顯低于傳統方法預測集裝箱船港口作業時間的APE。從表7中可以看出,傳統預測方法的最大APE是10.3%,MAPE是4.5%;神經網絡模型的最大APE是7.1%,MAPE是1.6%,這說明了用神經網絡預測集裝箱船港口作業時間比傳統方法更精確。 圖3 神經網絡和傳統方法預測值的APE 表7 測試集最大APE和MAPE % 本文基于傳統預測集裝箱船港口作業時間方法的預測精度低、不靈活等問題,分析了集裝箱船港口作業時間受多種因素的影響、存在非線性的特點,結合神經網絡非線性擬合能力強的特點,構建神經網絡集裝箱船港口作業時間模型。通過與傳統預測方法預測效果的對比,展現了本文模型的優越性,提高了預測的精度,為制作科學高效的泊位計劃奠定了基礎。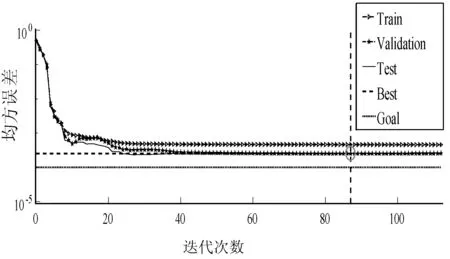
4 結 語

