循環次數對主軸承磨損仿真結果的影響研究*
杜祥寧,張艷艷,刁子宇,孫楠楠,張恒靖,劉震濤
(1.內燃機可靠性國家重點實驗室,山東 濰坊 261061;2.浙江大學 動力機械及車輛工程研究所,浙江 杭州 310027;3.浙江方圓檢測集團股份有限公司,浙江 杭州 310027)
0 引 言
隨著現代內燃機新技術的開發和內燃機功率密度的不斷提高,對于內燃機機械系統零部件的可靠性和耐久性的要求也逐漸提升。
主軸承作為內燃機曲軸的位置校準和支承部件,在服役過程中承受了很高的非穩定機械和熱負荷[1-2],直接影響了內燃機的工作性能及壽命。因此,對于主軸承—曲軸軸頸摩擦副的磨損失效預測進行研究具有重要意義。隨著計算機技術的發展,基于計算機輔助設計的數字仿真技術已經開始廣泛應用于內燃機研究、設計和開發的諸多領域[3]。然而,由于內燃機的實際工況復雜,影響因素眾多,為保證仿真計算的可信性和可驗證性,對于數值模型的適用性、邊界條件的合理性、計算方法的靈活性等均提出了更高的要求[4-5]。
磨損輪廓作為磨損仿真模型中的重要幾何參數,其在仿真計算中的更新頻率,對于磨損仿真結果的可信性起著至關重要的作用,也直接決定了磨損仿真的計算效率。重慶大學的許立新等[6]提出了一種基于磨損輪廓的不斷更新的、含間隙旋轉鉸的動力學建模方法,并以平面滑塊曲柄機構為例,利用數值模擬和實驗測試的方法,研究了曲柄—連桿副的動態響應和磨損特性;KIM D等[7]通過建立線性滑軌的表面磨損和損傷累積綜合數值模型,對滑軌構件表面沿垂直方向的磨損量進行了計算,并開發了一種外部幾何更新算法(GUA),實現了磨損計算過程中滑軌內槽表面磨損輪廓的更新,從而提高了數值模擬的精度。
本文以某型號服役柴油機的主軸承為研究對象,通過主軸承磨損仿真模型中,簡化工況參數的設計和仿真結果的比較,研究不同循環次數的取值對于磨損仿真計算結果的影響規律,最后給出兼顧計算成本及可信性的循環次數的建議取值。
1 磨損仿真模型建立
1.1 曲軸系多體動力學潤滑耦合模型
本研究以某型號服役柴油機為模擬對象,發動機性能參數如表1所示。
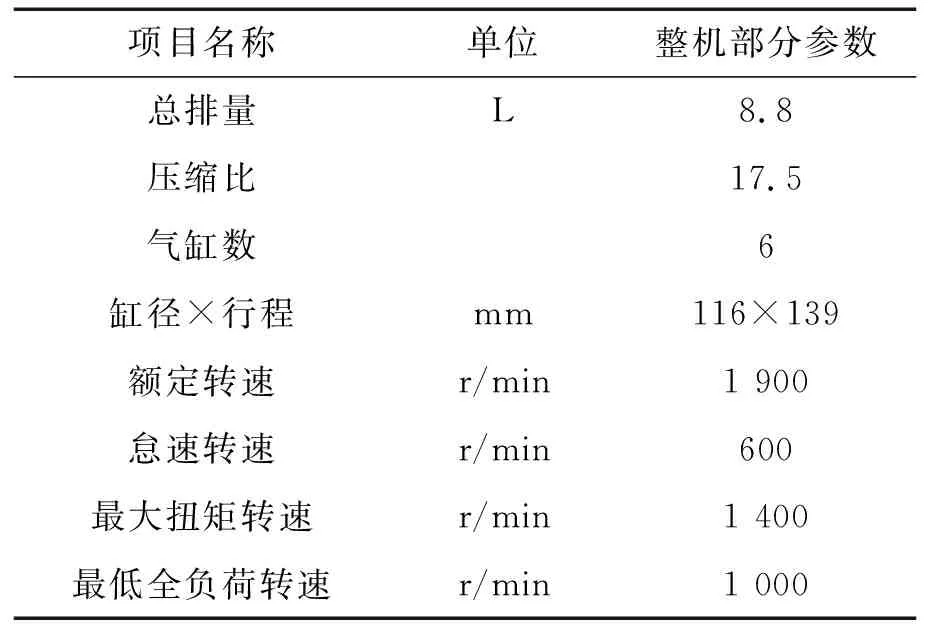
表1 發動機性能參數
軸承副元件材料屬性如表2所示。
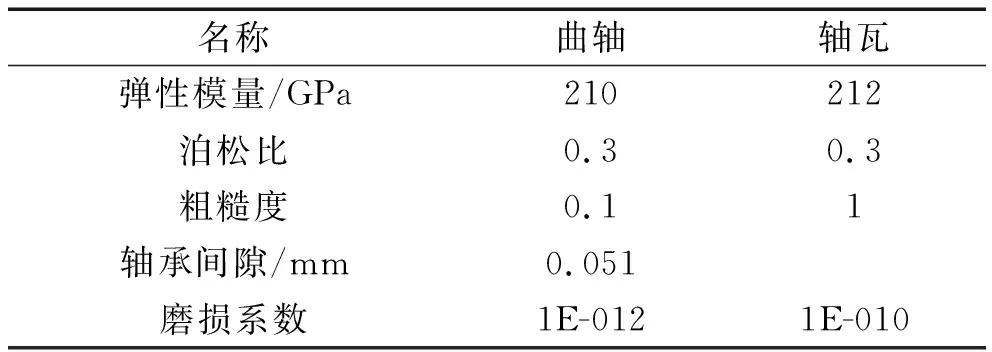
表2 軸承副元件材料屬性
本研究采用多體動力學仿真軟件AVL_EXCITE,建立了該型柴油機曲軸系的多體動力學潤滑耦合模型,曲軸系多體動力學模型如圖1所示。
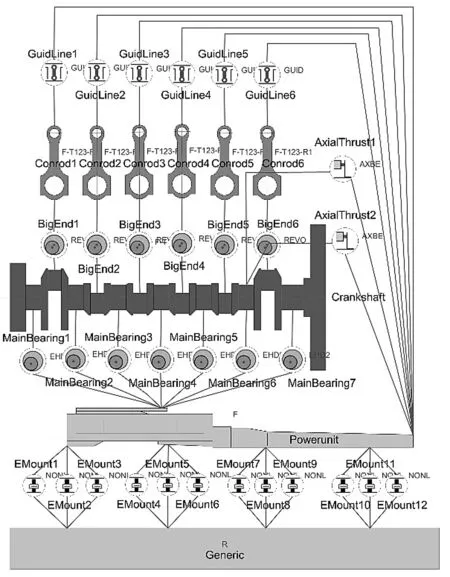
圖1 曲軸系多體動力學模型
模型中主要包括曲軸、連桿、機體、活塞、底座等部件,曲軸-軸承副及活塞-缸套副簡化為非線性連接;其中,筆者對曲軸、連桿和機體等部件進行了柔性處理,活塞、底座等均作為剛性體進行模擬。
筆者首先對曲軸、連桿、機體等主要部件進行三維建模和有限元前處理;其次,使用動態子結構法,對曲軸系關鍵部件進行主節點壓縮和主自由度提取,以簡化復雜的曲軸系建模和求解過程[8]。
為模擬主軸承的混合潤滑狀態,本文采用了考慮潤滑油填充率的平均雷諾方程,作為主軸承潤滑的理論基礎;同時,進行油膜潤滑—粗糙接觸邊界條件的判定,和不同潤滑狀態下接觸壓力的計算,以實現曲軸系的動力學、摩擦學耦合仿真。
1.2 主軸承磨損仿真計算
主軸承磨損量的計算和磨損輪廓的重建,應用了基于粘著磨損機理的經典Archard磨損理論模型[9]。
磨損相關變量間關系如下式所示:
(1)
式中:V—磨損體積,m3;K—考慮粘著磨損和磨粒磨損作用的主軸承磨損系數;s—接觸面上節點的相對滑動距離,m;FN—法向接觸載荷,N;H—較軟材料的布氏硬度,N/mm2。
本文研究的主軸承磨損量實際為徑向磨損深度,因此在式(1)兩邊同時除以磨損面積。
考慮到相對滑動距離非常小,將式(1)寫成微分形式,如下式所示:
(2)
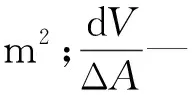
其中,節點間接觸壓力p沿滑動方向的變化可表示為相對滑動距離s的函數p(s)。
主軸承徑向磨損深度的微分形式如下式所示:
(3)
在主軸承的子結構模型中,各節點的幾何參數信息中包含了一組徑向位置初值。由于磨損過程是動態的,節點的徑向位置在磨損深度的迭代計算和磨損輪廓的更新過程中不斷變化;節點處的磨損深度也在不斷累積,對時間積分得到磨損深度的累積值如下式所示:
hj=hj-1+KdpjΔsj
(4)
式中:hj—某特定節點在第j時刻的累積磨損深度,m;hj-1—某特定節點在第j-1時刻的累積磨損深度,m;Kd—線磨損系數,用于徑向磨損深度的計算模型,Kd=K/H;pj—該節點在第時刻的接觸壓力值,MPa;Δsj—第j-1到第j時刻期間該節點與另一接觸面上對應節點的相對滑動距離,m。
將油膜壓力或粗糙接觸壓力分布等動力學仿真結果代入磨損模型,進行磨損量計算和磨損輪廓重建。由于主軸承磨損輪廓的動態更新過程與曲軸系的動力學特性變化之間存在相互影響的關系[10,11],在利用Archard磨損模型求得接觸面上各節點的磨損深度后,還需要將更新后的磨損輪廓作為幾何參數代入多體動力學模型中。
2 磨損仿真簡化工況設計
本研究中磨損仿真工況設計的依據來源于某型柴油機的整機耐久試驗測試工況,以考核整機可靠性和性能的穩定性。
試驗循環工況條件如表3所示。

表3 試驗循環工況條件
試驗循環工況中的最大負荷為全負荷的105%,最大爆發壓力為20 MPa,轉速分布600 r/min~2 150 r/min之間。耐久試驗持續時間為500 h,循環工況周期為2 400 s。
如需完全模擬耐久試驗的500 h循環工況,磨損仿真計算的循環周期為2 400 s,即共需模擬750個循環工況,磨損輪廓共迭代更新3 750次。
工作站處理器性能參數如表4所示。

表4 工作站處理器性能參數
在計算步長設定為0.062 5 deg的情況下,工作站每完成一次迭代計算,所需時間約為2 h~3 h;以15元/h為基準估算其計算成本,可得完全模擬750個循環工況所需時間約為312.5天~468.75天,計算成本達到11.25萬元~16.875萬元。可見,完全模擬耐久試驗的750個循環工況會導致仿真計算量巨大,且計算成本過高。
因此,有必要對磨損仿真工況進行簡化,即在保證一定仿真計算可信度的前提下,調整磨損仿真計算的循環周期,減少循環次數。
仿真簡化工況設計如表5所示。

表5 仿真簡化工況設計
3 磨損仿真計算結果分析
本文根據仿真簡化工況,將500 h全工況分配到1、2、3、5、10個循環中,分別進行磨損仿真計算,通過比較最大磨損深度的數值和全工況仿真后的磨損輪廓,評估了不同循環次數下磨損計算結果的變化規律。
3.1 最大磨損深度分析
徑向磨損深度是磨損的重要評價指標之一,本文對7個主軸承在不同磨損輪廓更新周期下經過500 h磨損仿真得到的最大磨損深度量進行比較和分析。
為體現循環次數變化對磨損仿真計算可信度的影響,根據循環次數間最大磨損深度的相對偏差值,定義某循環次數i的磨損計算偏差率εi如下式所示:
(5)
式中:hi—循環次數為i時的最大磨損深度,m;hj—相鄰較大循環次數時的最大磨損深度,m。
最大磨損深度h隨著循環次數N變化的關系可由擬合所得曲線看出。
第1~7主軸承最大磨損深度如圖2所示。
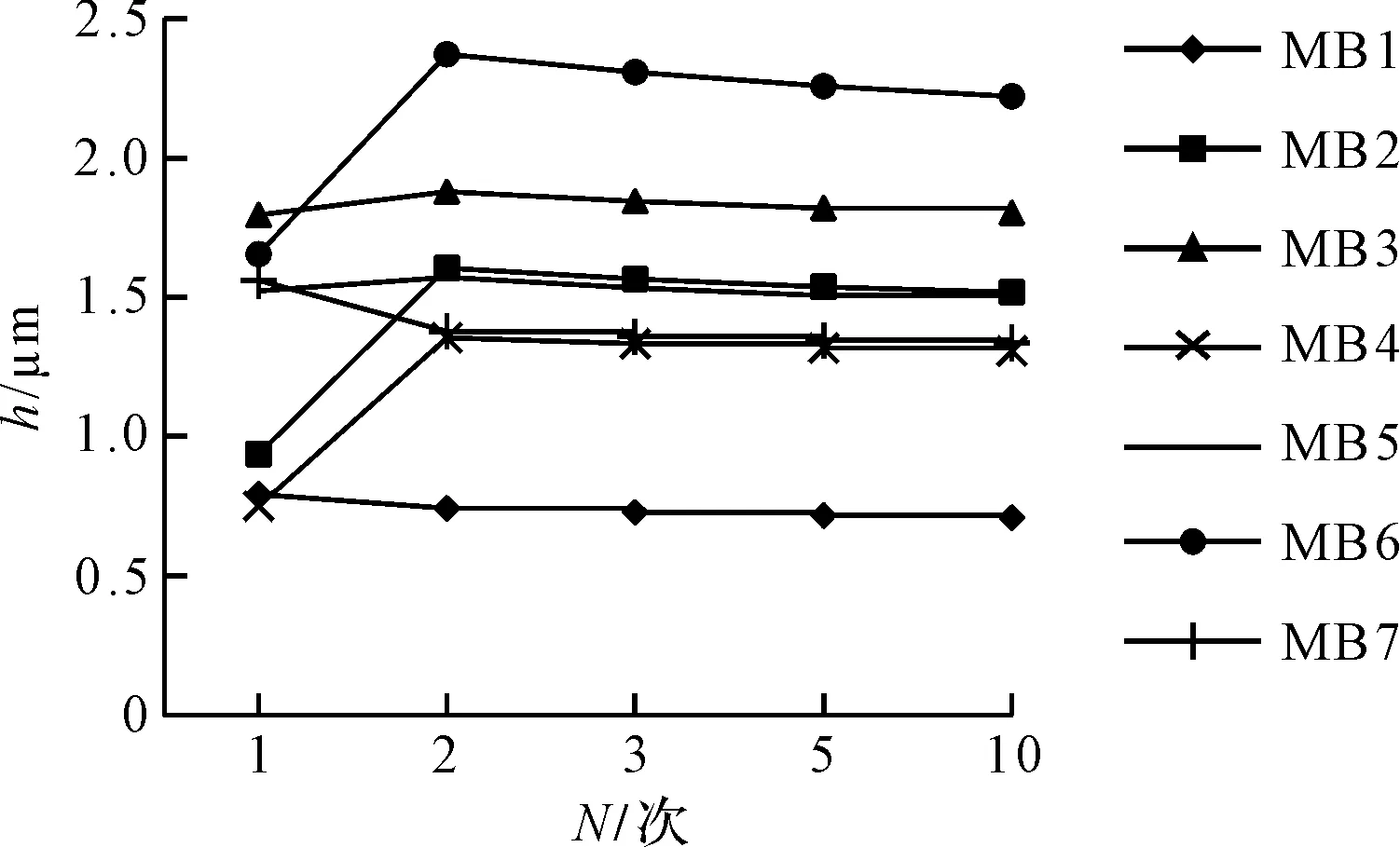
圖2 第1~7主軸承最大磨損深度
隨著循環次數N的增大,最大磨損深度基本趨于收斂。當N=3時,最大磨損深度的偏差率最大值約為2.8%;當N=5時,最大偏差率約為1.6%。
因此,綜合考慮磨損預測仿真工作中的計算成本和可信性要求,在本文建立的磨損仿真模型中,選擇循環次數N=3進行仿真簡化工況設計和磨損計算,已經可以在保證一定磨損仿真計算可信度的同時減少計算量,節約計算資源和成本。
3.2 磨損輪廓分析
利用MATLAB做出在不同循環次數下,經過500 h全工況磨損仿真后,第1~7主軸承的磨損輪廓。經分析得出,其中第3主軸承和第6主軸承整體磨損最為嚴重,第1主軸承磨損量較小。
由于循環次數N大于2時,各循環次數對應的磨損輪廓基本重合。以下只對N=1和N=3時,第3和第6主軸承的磨損輪廓特征進行比較。
N=1、3時,第3、6主軸承磨損輪廓如圖(3~6)所示。
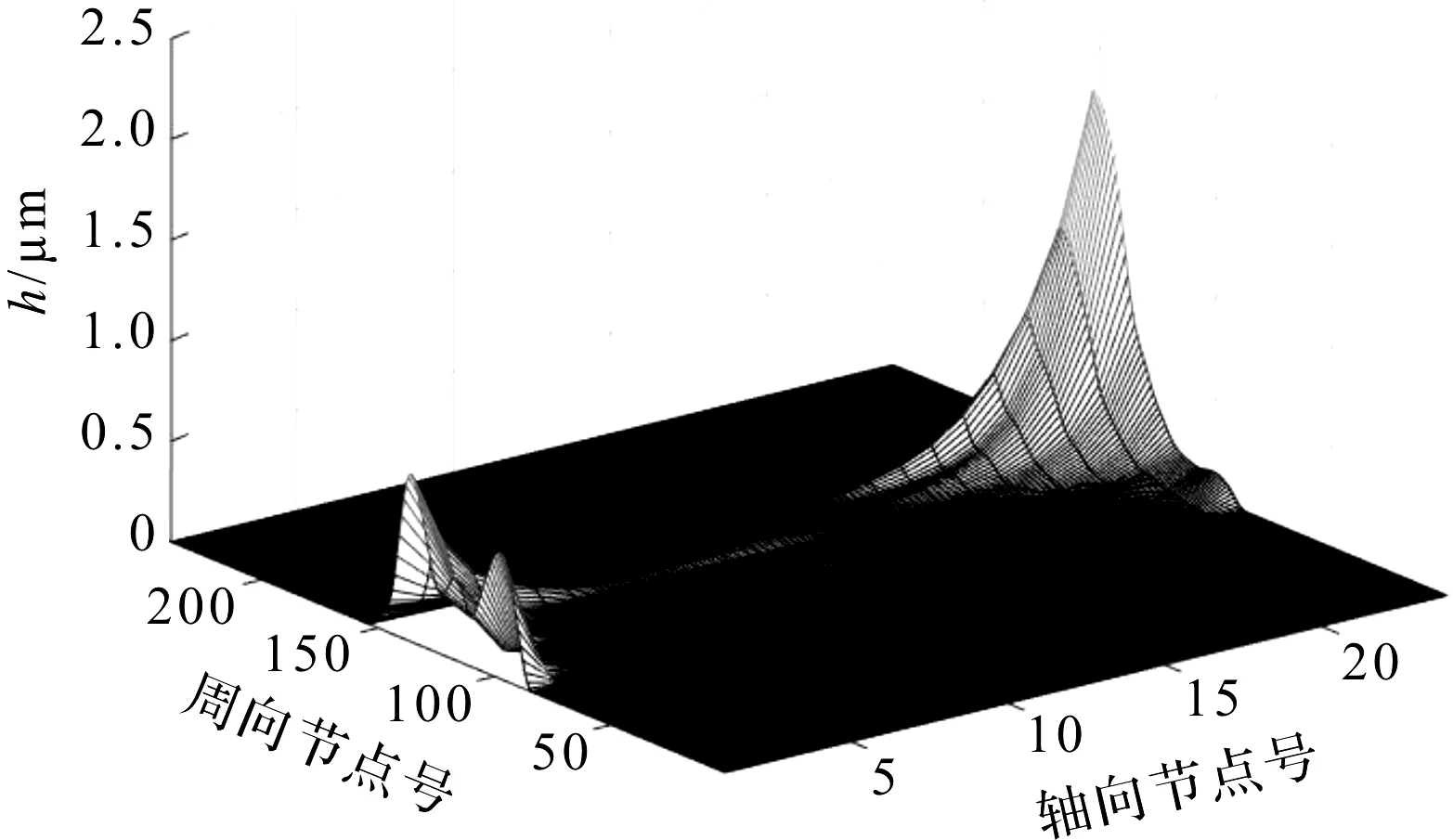
圖3 N=1時第3主軸承磨損輪廓

圖4 N=3時第3主軸承磨損輪廓
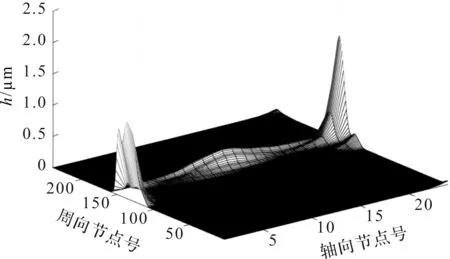
圖5 N=1時第6主軸承磨損輪廓

圖6 N=3時第6主軸承磨損輪廓
從圖(3~6)可以看出:循環次數的變化對于第3、6主軸承磨損輪廓的大致形狀基本沒有影響;其中,2個主軸承的磨損峰值都主要分布在軸向左、右兩端。
第3主軸承左、右側磨損峰值分別如圖(7,8)所示。

圖7 第3主軸承左側磨損峰值
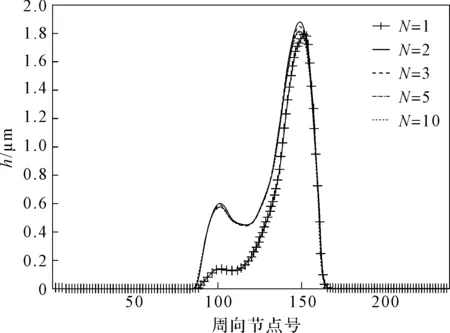
圖8 第3主軸承右側磨損峰值
對于第3主軸承,隨著循環次數從1增加到3,磨損輪廓的仿真結果主要表現為:軸向中間節點位置的磨損程度加劇,但主要磨損區域的周向節點范圍基本沒有變化。左側磨損峰值的個數減少,數值增加;右側峰值的大小沒有明顯變化,但其他周向位置的磨損量明顯增加。
第6主軸承左、右側磨損峰值分別如圖(9,10)所示。
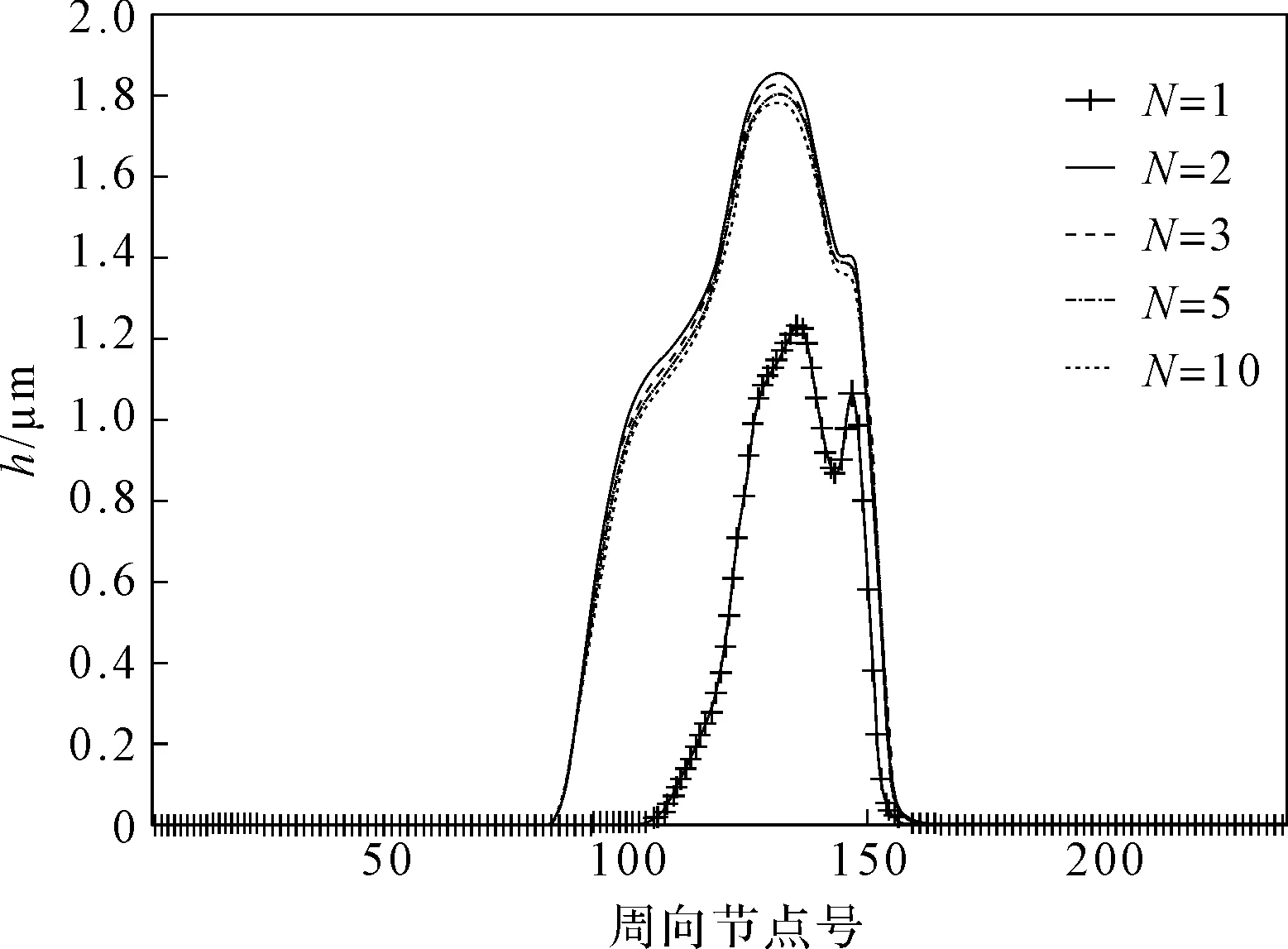
圖9 第6主軸承左側磨損峰值
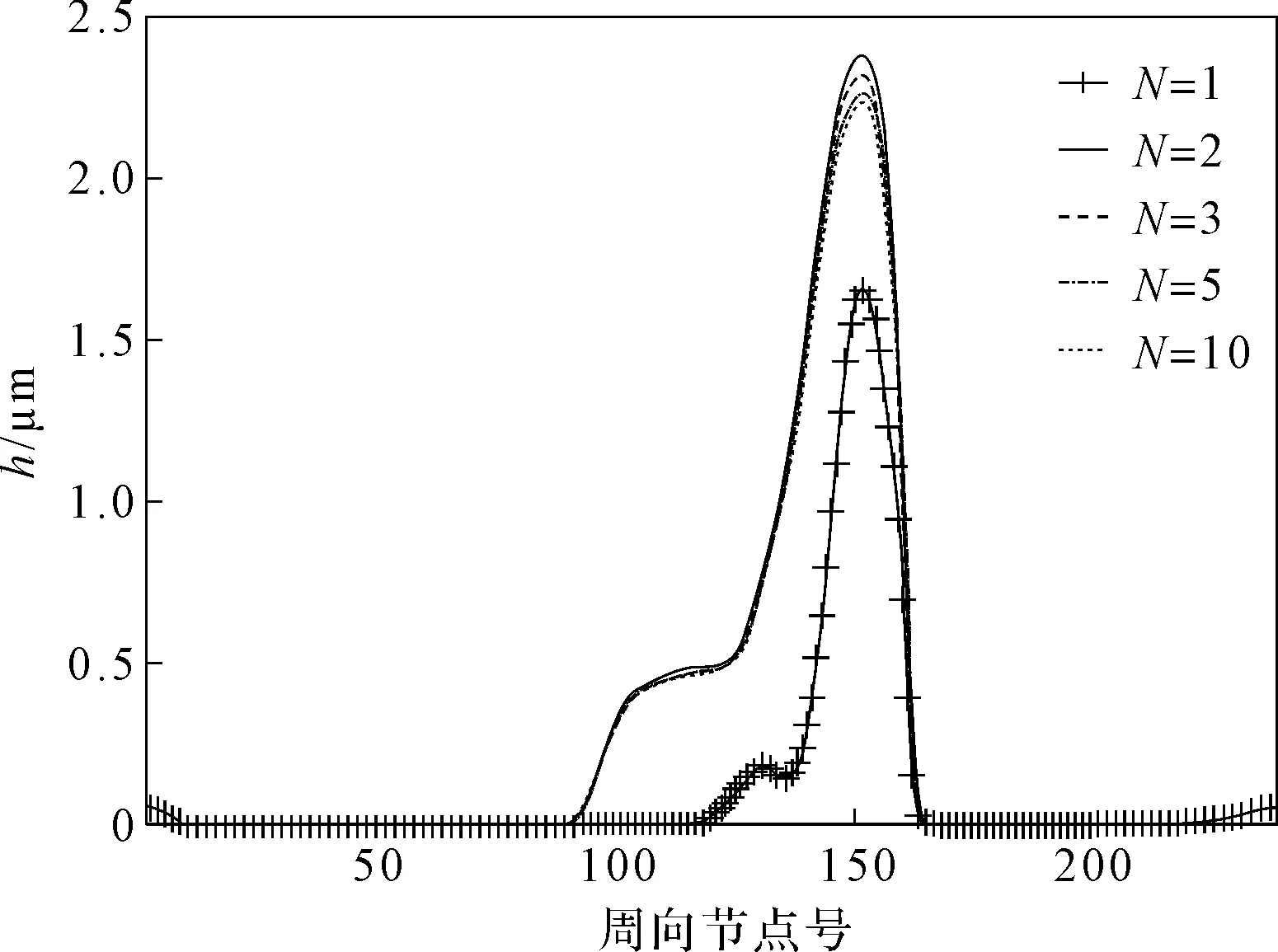
圖10 第6主軸承右側磨損峰值
對于第6主軸承,循環次數的增大不但擴大了主要磨損區域的周向節點范圍,還提高了軸向左、右兩端的磨損峰值。由此可見,在磨損仿真計算過程中,選取適當的循環次數對于提高仿真計算的可信度很有必要。
4 結束語
本文以某型號服役柴油機的主軸承為例,采用了多體動力學仿真的方法,建立了主軸承磨損計算模型,設置了多組不同循環次數下的簡化工況,并進行了磨損仿真計算,研究了仿真簡化工況設計中循環次數的取值對于主軸承磨損仿真計算結果的影響規律,并探討了仿真簡化工況設計中循環次數的適當取值。得出以下結論:
(1)在本文建立的磨損仿真模型中,選取循環次數N=3進行仿真簡化工況設計和磨損量計算,可以在保證一定計算可信度的同時減少計算量;
(2)隨著循環次數N的增加,最大磨損深度的計算結果趨于收斂;當N=3時,最大磨損深度的偏差率最大值約為2.8%;當N=5時,最大偏差率約為1.6%;
(3)隨著循環次數的變化,第3、6主軸承的磨損輪廓大致形狀沒有變化,但其磨損峰值的個數、大小以及主要磨損區域的周向分布范圍均會受到影響。
由于不同型號和工況條件下,柴油機的機械結構、材料特性和運行參數不同,其對應建立的磨損仿真模型的關鍵參數和工況設計策略也會相應變化。因此,以上工作只針對某系列柴油機在部分特定循環工況載荷下,對循環次數對于主軸承磨損仿真計算可信度的作用規律進行了研究。
關于其他更多機型及工況條件下,循環次數的具體取值及其相應變化機制等問題,亟待后續研究和討論。

