不同負載特性下的全工況電流互感器仿真研究

蘇 賢 項宇鍇

不同負載特性下的全工況電流互感器仿真研究

蘇 賢1項宇鍇2

（1. 國網漳州供電公司，福建 漳州 363000；2. 國網龍巖供電公司，福建 龍巖 364000）

電磁式電流互感器磁滯建模是分析電磁式電流互感器傳變特性的重要理論工具。本文詳述了Jiles-Atherton模型磁滯建模的數學機理，依據電磁式電流互感器等效電路圖推導出勵磁電流時域微分方程，基于Jiles-Atherton模型與勵磁電流時域微分方程建立電磁式電流互感器仿真模型，利用Simulink編程實現電磁式電流互感器磁滯建模，在磁心處于線性、飽和工況以及二次側搭載不同負載的情況下進行仿真，電流傳變仿真結果表明論文模型能夠正確表征電磁式電流互感器在實際運行中一二次電流存在相位差的傳變誤差特性以及二次側不同負載時的傳變規律，為電流互感器應用設計及故障分析提供理論依據。

Jiles-Atherton模型；電磁式電流互感器；Simulink；時域微分方程；勵磁電流

0 引言

電磁式電流互感器是用于配電網中計量、保護、測量的重要傳感元件，認識其傳變特性對于提高網架故障分析效率及其設計應用具有重要意義。電磁式電流互感器傳變特性與其鐵心自身的磁滯特性密切相關，因此磁滯建模是剖析電磁式電流互感器傳變規律的重要手段。

在磁滯建模領域，Jiles-Atherton模型因其計算的參數較少，物理意義明確，在利用電磁感應的設備建模中被廣泛使用[1-6]，有若干將Jiles-Atherton模型拓展為鐵磁傳感設備數值計算模型的文獻見諸于報道，取得了不錯的建模效果[6-13]。文獻[6]考慮了直流偏磁，在Jiles-Atherton模型的基礎上引入直流磁場對磁化建模表達進行了修正。文獻[7]率先將Jiles-Atherton模型引入電流互感器的磁滯建模當中，依據等效電路圖對模型的數值求解公式推導進行了初步探索。文獻[8]沿用了文獻[7]的數值計算公式，而在模型參數獲取方面引入了一種混合遺傳模擬退火算法。文獻[9]在ATP-EMTP軟件中利用TACS模塊實現了電流互感器的Jiles-Atherton磁滯建模，但文獻以一次電流作為初始勵磁電流反推出感應電壓后對電路進行反饋求解的方式缺乏明確的物理意義。文獻[10]給出了勵磁電流包含磁化微分項的微分方程，然而微分方程中存在電壓變量，與實際勵磁電流決定感應電壓的客觀事實不符。文獻[11]在推導過程中剔除了電壓變量，直接給出二次電流包含磁化微分項的微分方程，但其后續論證中只給出了純電阻情況下的飽和仿真結果。綜上所述，對于電流互感器傳變建模的研究多集中于傳變微分方程的推導以及實現求解的方式等方面，在傳變仿真內容方面的研究范圍僅限于傳感元件在全工況下帶單一負載的情況，沒有做到在不同工況帶不同二次負載的情況下進行全面的傳變特性建模分析。

全面的建模分析有利于在廣度上加深對電磁式電流互感器的傳變規律的認識，因此，本文利用Simulink編程環境建立電磁式電流互感器磁滯模型及全工況仿真平臺，仿真并分析電磁式電流互感器在不同運行工況下配以不同負載時的傳變特性。

1 Jiles-Atherton磁滯建模數學機理

表征非磁滯磁化的郎萬之函數為

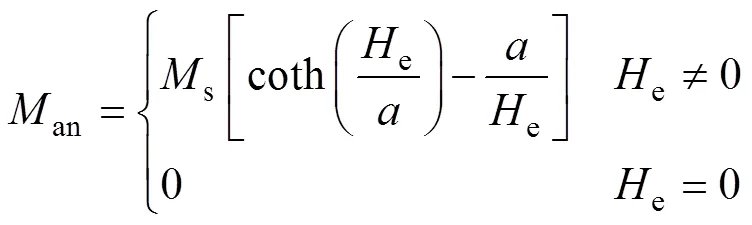
式中：an為非磁滯磁化強度；s為飽和磁化強度；e為計及耦合效應的等效外施磁場強度；為無序化參數，反映了材料內部的熱運動。郎萬之函數描述的非磁滯磁化曲線，其基本特征是非磁滯磁化強度在較小的等效外施磁場范圍內呈現出線性增長趨勢，隨著等效外施磁場的不斷增加，達到飽和，如圖1所示。

在郎萬之函數的基礎上引入可逆磁化和不可逆磁化的概念

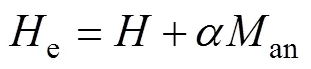
（3）

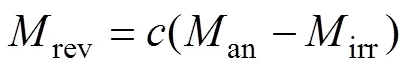
式中：為磁場強度；為耦合系數，表征非磁滯磁化強度對于等效磁場強度的貢獻程度；為磁滯情況下的磁化強度；irr為不可逆磁化分量；rev為可逆磁化分量；為可逆磁化系數。

不可逆磁化分量對于磁場強度的微分為

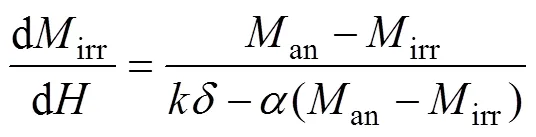
式中：為損耗系數；為磁場強度的方向系數，當d/d＞0時，取1，反之，取0。

將上述五式進行變量代換，得到Jiles-Atherton磁滯模型的主微分方程

上述主方程在(an-)＜0時有效，在(an-)＞0時，將上述微分方程修正為

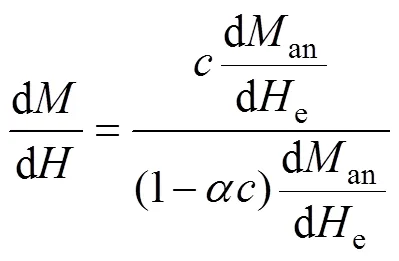
2 基于J-A模型的電磁式CT磁滯建模

2.1 電磁式CT結構及原理

電磁式電流互感器的基本原理與變壓器一致，可以看作一次側注入理想電流源，二次側短路的變壓器。如圖2所示，這是電磁式電流互感器在運行過程中的典型結構。圓形鐵心穿過一次線纜，鐵心置身于一次線纜電流形成的環形磁場之中，在二次側感應出按匝比倍數減小的電流，通常額定情況下為5A。

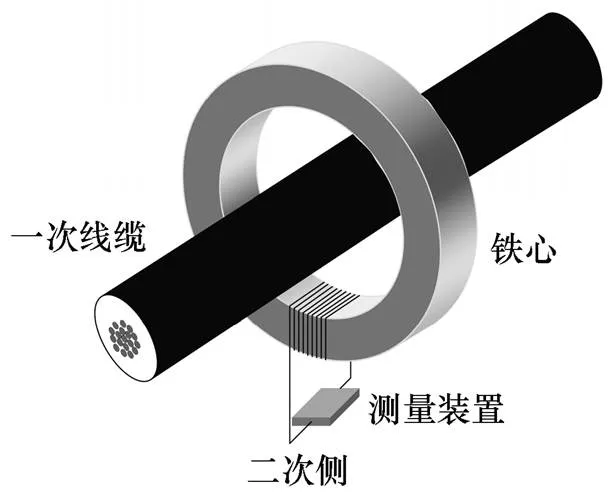
圖2 電磁式CT結構圖

2.2 CT磁滯建模

理想的電磁式電流互感器一二次電流比與一二次匝比為反比，但實際中，一次電流的一小部分需要作為勵磁電流為二次電動勢的感生提供勵磁。如圖3等效電路所示，它們之間滿足

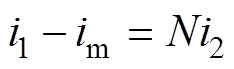
式中：1為一次電流；m為勵磁電流；2為二次電流；為二次繞組匝數。由等效電路圖可得出二次電壓與二次阻抗滿足

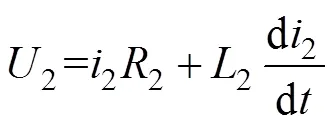
式中：2為二次感應電勢；2為二次總電阻，包括線路電阻以及負載電阻；2為二次總電感，包括漏感及負載電感。另外，從電磁感應原理的角度來理解二次感生電壓可得

聯立式（9）、式（10）可將電流與磁鏈變化聯系起來，再根據磁感應強度與磁場強度、磁化強度關系式（11）以及安培環路定律式（12）可得出勵磁電流依賴于一次電流1、勵磁電流m以及磁化強度對于磁場強度微分d/d的時域微分方程。

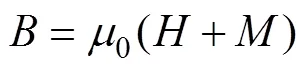
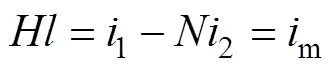
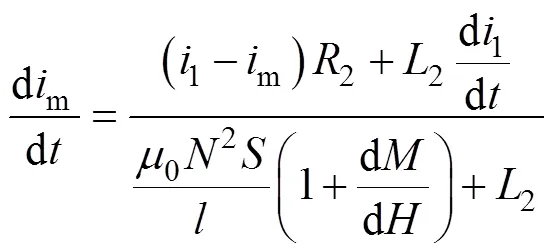
解上述微分方程可解得勵磁電流，從而獲取二次電流，獲悉電流互感器的傳變特性。

3 電磁式CT的Matlab建模仿真

3.1 電流互感器模型的Matlab實現

利用Matlab求解上述時域微分方程，可以直接編寫.m文件或形成狀態方程在Simulink環境下利用s-function創建仿真模塊，利用s-function創建仿真模塊可以避免繁瑣的語言編碼，本文利用s-function來實現電磁CT的建模仿真。

求解式（13）的同時需要同步求解出磁化強度，以便獲取d/d。磁化強度依賴于勵磁電流的時域微分如式（14）所示。

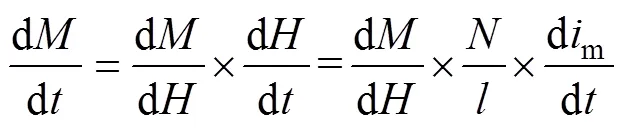
式（13）、式（14）形成狀態方程組

一次電流1作為輸入變量，勵磁電流m以及磁化強度作為狀態變量，二次電流2作為輸出變量。基于s-function模塊編寫電磁式電流互感器磁心模塊后用subsystem模塊對其進行一次封裝。封裝后的磁心模塊為一個三端模塊，如圖4所示，左側兩個端子分別為二次進線端子以及接地端子，右側端子為二次出線端子。封裝好的磁心模塊再與linear transformer模塊搭配封裝成電流互感器模塊，如圖5所示，該模塊為一個四端模塊，左側為一次進出線端子，搭接一次電流源，右側為二次進出線端子，搭接二次負載。

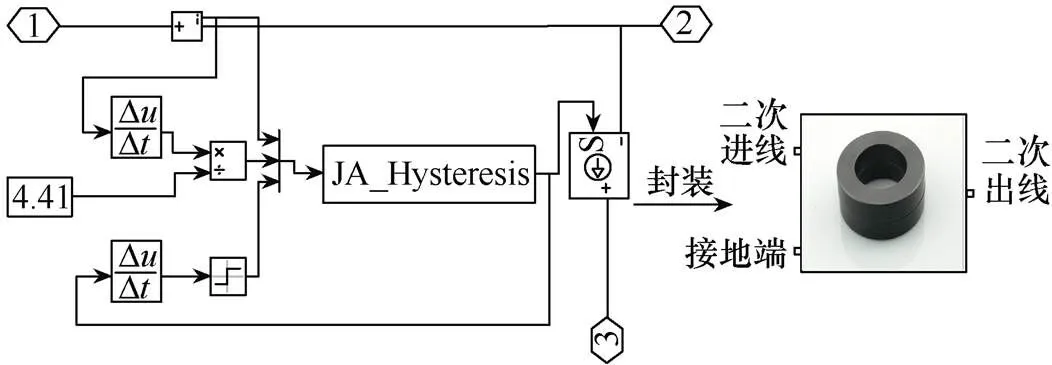
圖4 磁心模塊

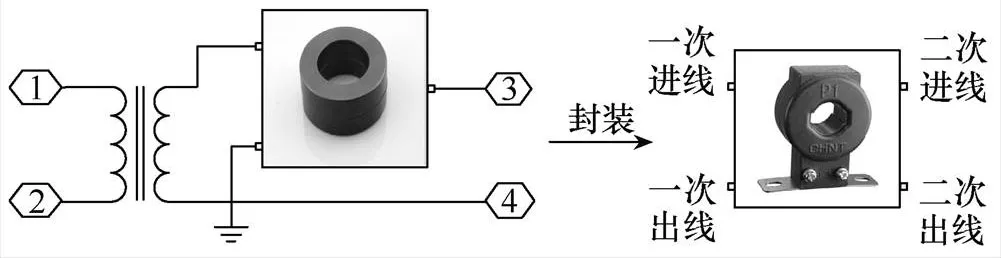
圖5 電流互感器模塊

本文依據文獻[10]提供的電流互感器磁滯參數作為本文仿真所用參數，具體參數值見表1[10]。該電流互感器型號為LZZBJ9—10C2GY，額定電流比75A/5A，額定二次負荷15V·A。

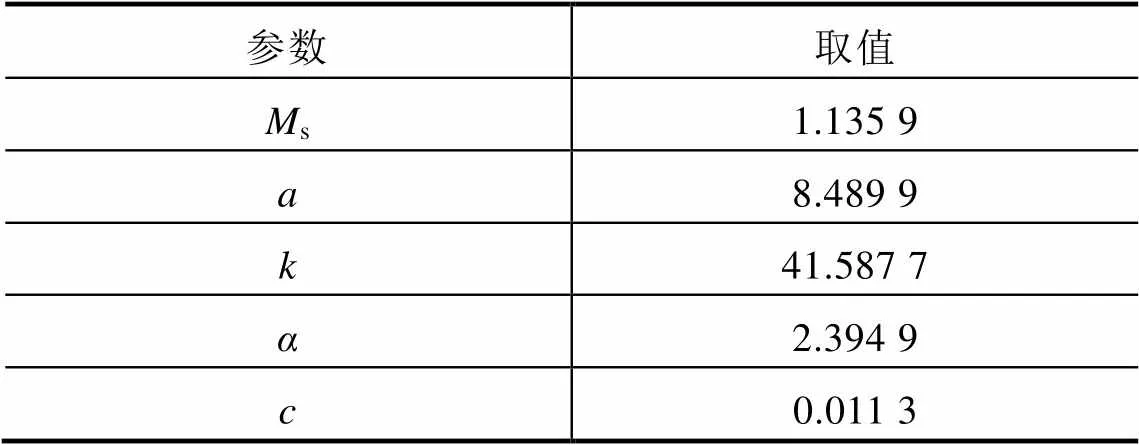
表1 磁滯參數

3.2 全工況仿真平臺

利用上述模塊，在Simulink中搭建全工況仿真平臺，如圖6所示，一次側直接配置仿真電流發生器，可任意調節電流幅值。二次側配置阻感性可調負載，可任意變換負載特性。依托該仿真平臺，本文針對電磁式電流互感器磁心在不同運行工況以及二次側搭載不同性質負載的情況下進行仿真實驗，仿真結果在第4節中給出。

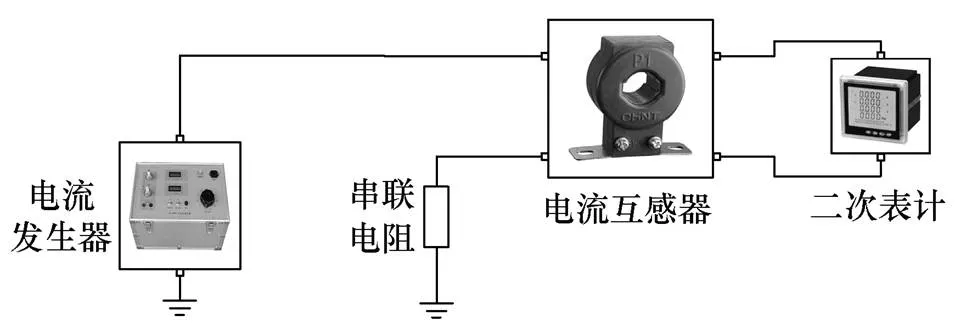
圖6 故障仿真平臺

4 仿真分析

4.1 未飽和工況仿真

施加200A的一次電流，磁心磁化特性、一二次電流及勵磁電流仿真結果如圖7（a）、圖7（b）、圖7（c）所示，200A的一次電流尚在參數所描述電流互感器的精確傳變范圍內，鐵心未飽和，磁滯回線層呈小回環狀，一次歸算電流與二次電流幅值、相位幾乎一致，勵磁電流波形接近正弦，勵磁電流不是完美正弦的原因是Jiles-Atherton模型仿真出的未飽和磁滯回線接近平行四邊形，而實際的未飽和磁滯回線為橢圓形[14]，考慮到實際應用中飽和工況的精度更為重要，因此該誤差可以接受。不同于基于單值磁化曲線的電流互感器模型[15]，由圖7（b）可以看出本文模型仿真出的一二次電流呈現一定的相位偏差，由于磁滯模型的引入，勵磁電流與一次電流變化不一致造成了這樣的相位偏差，達到了與實際電流互感器一二次電流存在相同相位差的仿真效果。

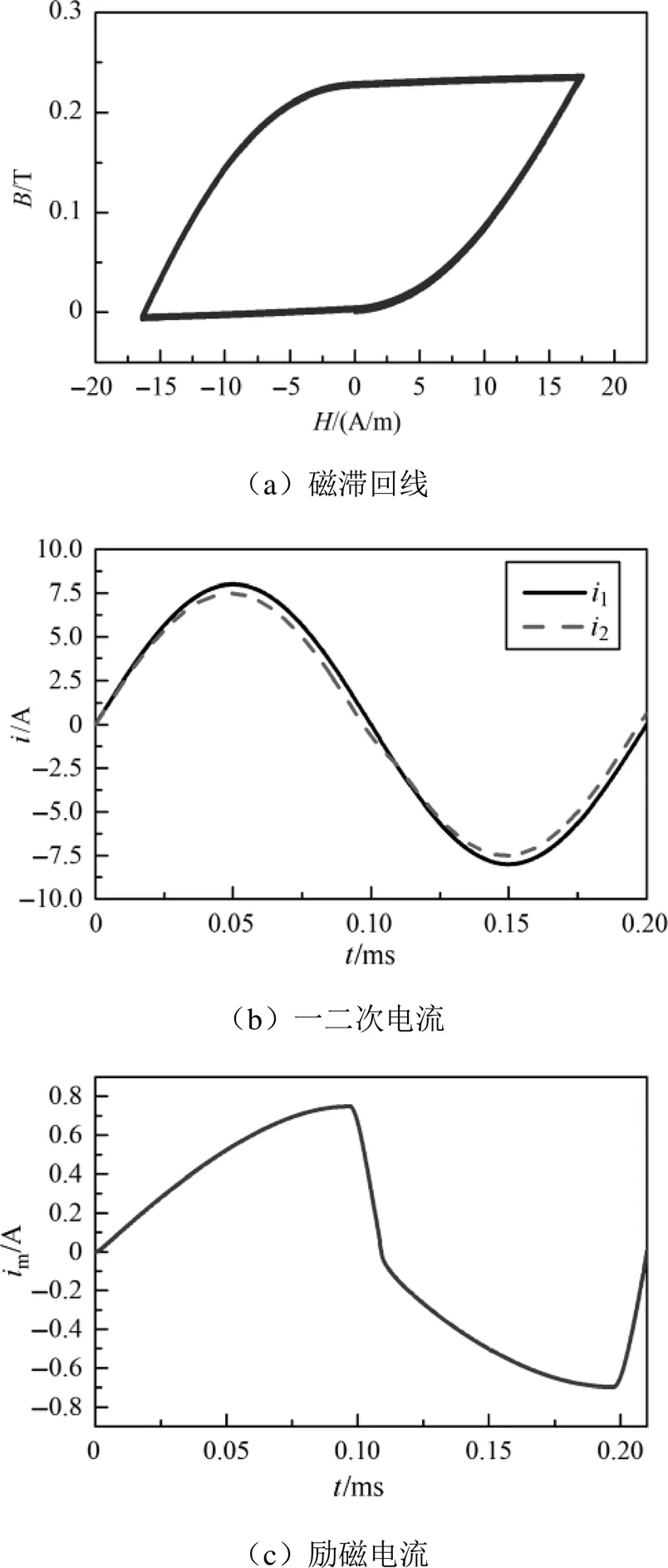
圖7 未飽和工況仿真波形

4.2 全飽和工況仿真

施加5 000A的一次電流，此時參數所描述的電流互感器鐵心已達到深度飽和，磁滯回線存在明顯拐點，磁場強度大幅增加，磁感應強度增長緩慢，趨近于停滯，圖8（b）二次電流波形在每半個周末內出現失真，鐵心磁感應強度達到拐點后不再線性增加，二次側無法感生出足夠匹配的感應電動勢來生成接近一次歸算電流的二次電流，二次電流趨近為零，此時一次電流幾乎全部用于勵磁，如圖8（c）所示，勵磁電流峰值接近一次歸算電流峰值，在拐點時刻，勵磁電流陡增，從幾安培陡增至接近200A。

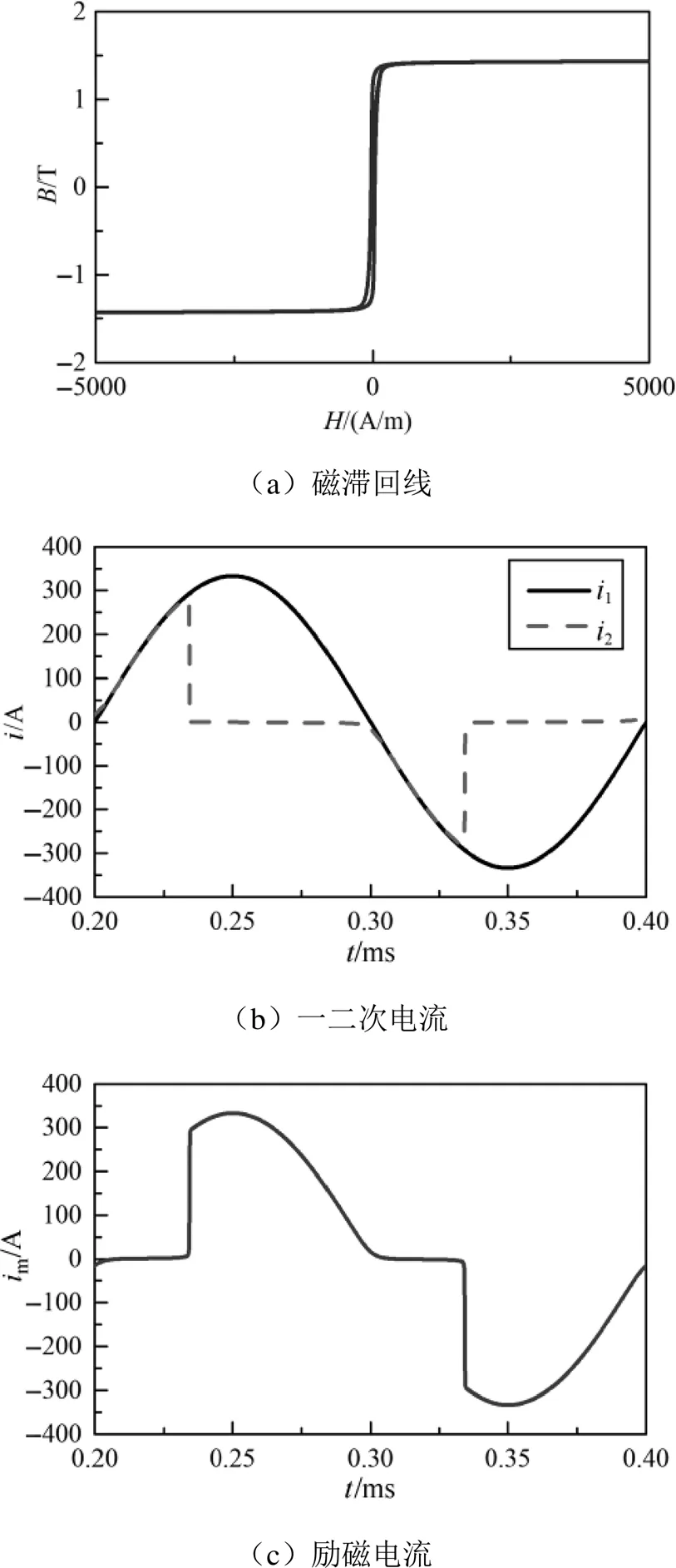
圖8 純電阻負載全飽和工況仿真波形

將二次負載參數更換為純電感負載，仿真獲得如圖9所示波形，飽和磁滯回線與純電阻負載情況相同。當二次負載為純電感負載時，磁心飽和時，因為電感的存在，在飽和區域，二次電流不能突變為零，其電流值保持為磁心剛剛進入飽和時的二次電流值，一直保持到一次電流反向下降至飽和時刻的一次電流值，此時鐵心離開飽和區域，回到線性區域，二次電流又重新同步一次電流的變化，從波形上看，二次電流波形被削平，呈平頂馬鞍形。

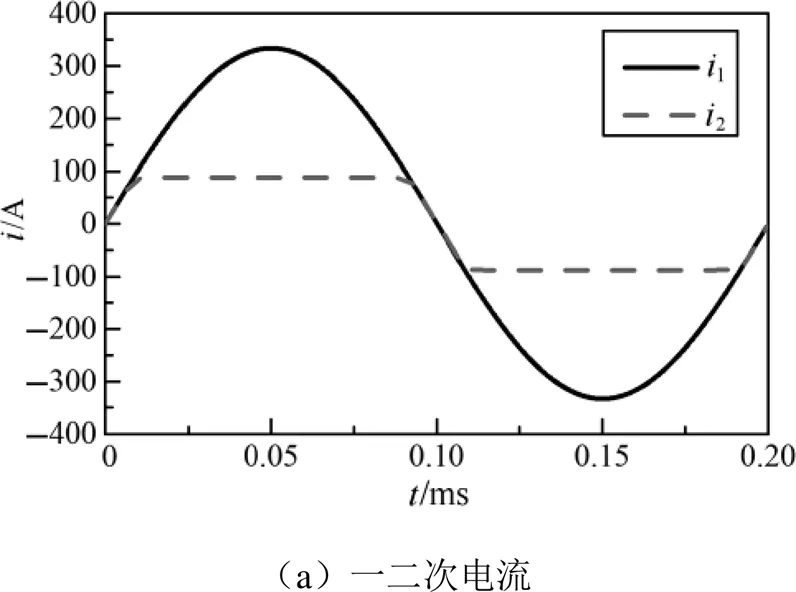
負載參數為阻感性時，仿真波形如圖10所示，由圖10（a）可知，二次電流在飽和時刻因為電感的存在，無法發生突變，在飽和時刻保持前一刻未飽和時的二次電流值不變，隨后二次電流進入一段指數衰減階段，一次電流值反向下降后需要降低到比飽和時刻更低時，才能夠脫離飽和區域，注意到，飽和二次電流的正負半波是對稱的，因此飽和二次電流不存在直流分量。本文純電感及阻感性負載在全飽和工況下的一二次電流仿真波形與文獻[16]中給出的波形特征一致，驗證了本文所述模塊的正確性及有效性。

4.3 不同二次負載工況仿真

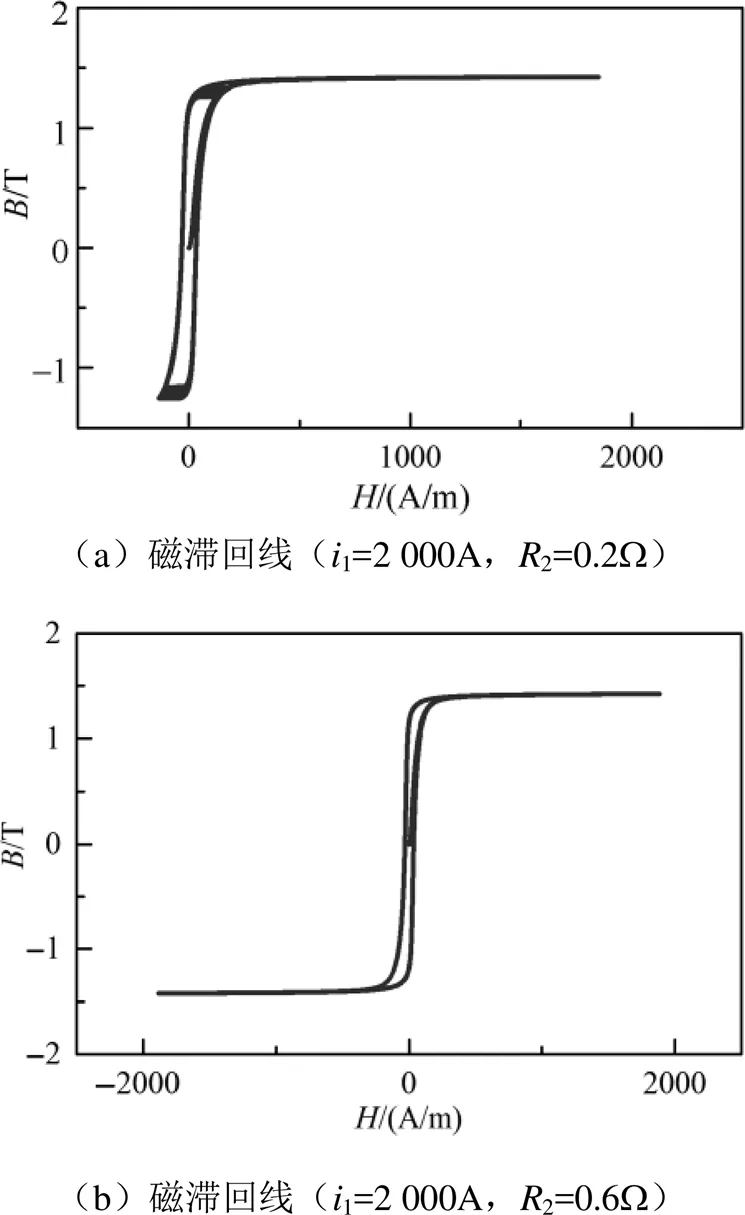
施加2 000A的一次電流，在不同負載情況下仿真電流互感器傳變特性，當二次負載為0.2W，鐵心未飽和，磁滯回線未出現拐點，圖11（a）中出現拐點是因為仿真初始階段均默認鐵心無剩磁，在零剩磁情況下，鐵心會快速飽和，隨著仿真的繼續，鐵心磁滯特性出現，電流互感器的半周波傳變范圍擴大，磁滯回線仿真快速回到線性區域，不再經過拐點。當二次負載為0.6W時，電流互感器進入傳變飽和區域，磁滯回線經過拐點，如圖11（b）所示。圖11（c）為兩種負載情況下電流互感器的二次電壓波形，二次負載為0.2W時，二次電壓波形接近正弦，二次負載為0.6W時，二次電壓波形出現畸變，傳變相同一次電流時，二次負載越大，需要感生的電壓越大，需要的勵磁越多，勵磁越多，越接近飽和區域，因此，適當的降低負載可以增加電流互感器傳變范圍，相反地，由式（10）可知，匝比越高，鐵心有效截面越大，電流互感器的帶載能力越強。

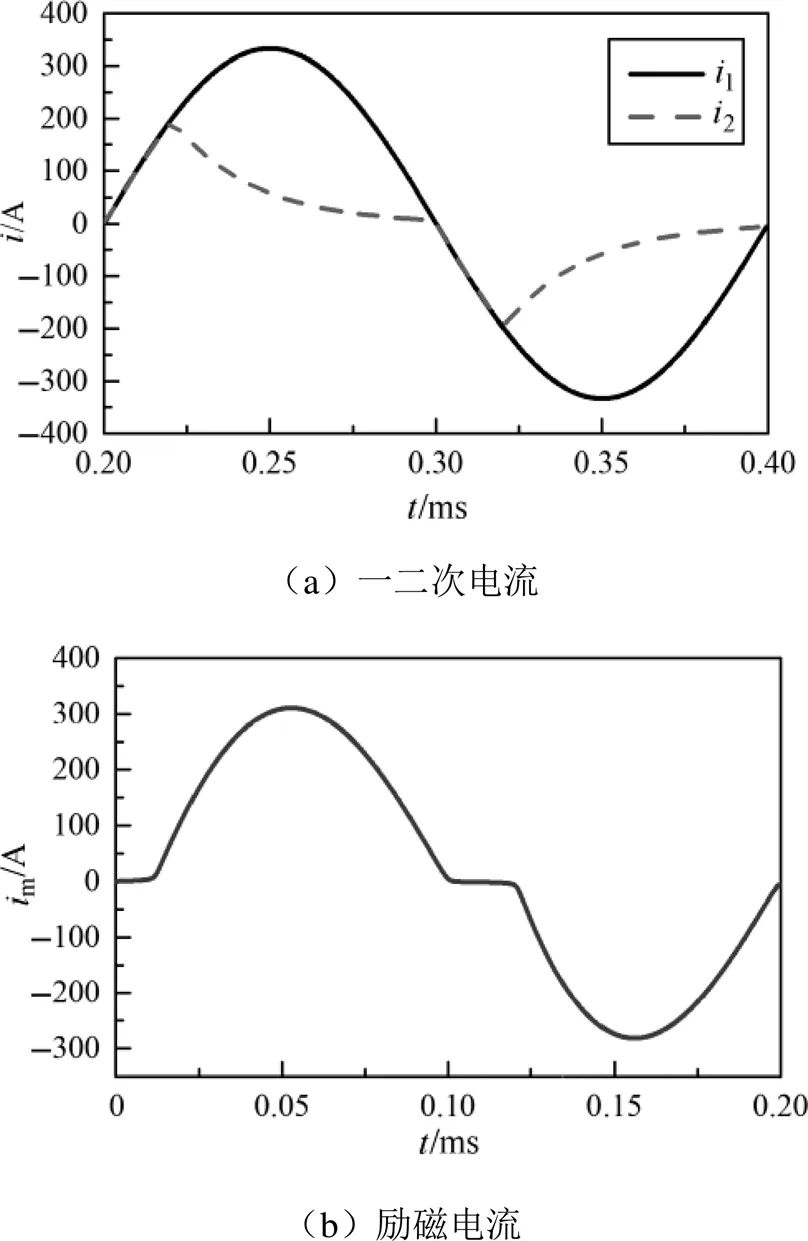
圖10 阻感性負載全飽和工況仿真波形

上述仿真結果表明本文電流互感器模型能夠正確表征電流互感器帶載變化時的傳變規律，可用于電流互感器在特定應用場合下的帶載設計。

5 結論

本文基于Jiles-Atherton磁滯模型結合勵磁電流時域微分方程建立電磁式電流互感器數值仿真模型，在Simulink環境下對電流互感器進行了全面的傳感現象仿真，一二次電流仿真結果表明磁滯模型的引入使得該模型能夠有效表征實際情況中一二次電流在傳變時存在相位差的傳感特性。飽和工況下配以不同二次負載的仿真結果表明，模型能夠正確反映二次側搭載不同屬性負載時引起的電流互感器飽和傳變規律變化。此外，本文建立的電磁式電流互感器模型在Simulink中便于模塊封裝，結合Simulink中其余電力專業模塊，方便用于實際電流互感器的設計仿真及故障分析，具有較高的實用價值及理論指導意義。

[1] 王洋, 劉志珍. 基于Jiles Atherton磁滯理論的直流偏磁下鐵心損耗預測[J]. 中國電機工程學報, 2017, 37(1): 313-322.

[2] 牛牧青, 楊斌堂, 楊詣坤, 等. 磁致伸縮主被動隔振裝置中的磁機耦合效應研究[J]. 力學學報, 2019, 51(2): 322-332.

[3] 陶風波, 張剛, 李建生, 等. 基于局部磁滯回線斜率的變壓器鐵心剩磁估算[J]. 變壓器, 2019(2): 27-33.

[4] 楊汾艷, 余超耘, 劉正富, 等. 基于實際工程的變壓器改進J-A模型研究[J]. 電力自動化設備, 2018, 38(4): 191-195.

[5] 劉任, 李琳, 王亞琦, 等. 基于隨機性與確定性混合優化算法的Jiles-Atherton磁滯模型參數提取[J]. 電工技術學報, 2019, 34(11): 2260-2268.

[6] 李長云, 劉亞魁. 直流偏磁條件下變壓器鐵心磁化特性的Jiles-Atherton修正模型[J]. 電工技術學報, 2017, 32(19): 193-201.

[7] KOTHEIMER W C, ANNAKKAGE U D, MCLAREN P G, et al. Discussion of “a current transformer model based on the Jiles-Atherton theory of ferromagnetic hysteresis” (closure to discussion)[J]. IEEE Transa- ctions on Power Delivery, 2000, 15(4): 1323-1324.

[8] YIN Xianggen, ZHANG Zhe, QI Xuanwei, et al. Modeling and analysis for practical CT based on transient test and parameter identification[J]. CSEE Journal of Power & Energy Systems, 2016, 2(4): 51-57.

[9] LIU T S, HUANG S R, et al. Using TACS functions within EMTP to set up current-transformer model based on the Jiles-Atherton theory of ferromagnetic hysteresis[J]. IEEE Transactions on Power Delivery, 2007, 22(4): 2222-2227.

[10] 李寧彩. 電流互感器建模及其飽和對線路保護影響研究[D]. 北京: 華北電力大學, 2015.

[11] 熊蘭, 周健瑤, 宋道軍, 等. 基于改進J-A磁滯模型的電流互感器建模及實驗分析[J]. 高電壓技術, 2014, 40(2): 482-488.

[12] JIANDONG D, HAO L, YANG L. Modeling and experimental validation of a dynamic regional satura- tion J-A model for protective current transformer[J]. International Journal of Electrical Power & Energy Systems, 2019, 105: 315-322.

[13] 雷陽, 段建東, 張小慶, 等. 電流互感器J-A模型參數辨識及大通流動模試驗[J]. 中國電機工程學報, 2016, 36(增刊1): 240-245.

[14] 陳利翔, 邵振國, 張逸. 電磁式電流互感器諧波比值誤差實驗與分析[J]. 儀器儀表學報, 2017, 38(4): 977-984.

[15] 崔迎賓, 譚震宇, 曹維達. 電流互感器鐵心磁化模型的比較與分析[C]//中國高等學校電力系統及其自動化專業第二十六屆學術年會暨中國電機工程學會電力系統專業委員會2010年年會, 上海, 2010: 1-5.

[16] 袁季修. 保護用電流互感器應用指南[M]. 北京: 中國電力出版社, 2004.

Simulation of current transformer under different load characteristics

SU Xian1XIANG Yukai2

(1. State Grid Zhangzhou Power Supply Company, Zhangzhou, Fujian 363000;2. State Grid Longyan Power Supply Company, Longyan, Fujian 364000)

Hysteresis modeling of electromagnetic current transformers is an important theoretical tool for analyzing the transmission characteristics of electromagnetic current transformers. This paper details the mathematical mechanism of hysteresis modeling of Jiles-Atherton model, derives the time-domain differential equation of excitation current according to the equivalent circuit diagram of electromagnetic current transformer, and establishes the electromagnetic current based on Jiles-Atherton model and the time-domain differential equation of excitation current Transformer simulation model. The Hysteresis Modeling of electromagnetic current transformer is realized by using Simulink programming. Simulation results of current transmission show that the model in this paper can correctly represent the transmission characteristics of primary and secondary current with phase difference in actual operation and the transmission law of secondary side with different loads, which provides theoretical basis for the application design and fault analysis of current transformer.

Jiles-Atherton model; electromagnetic current transformer; Simulink; differential equations in time domain; excitation current

2020-07-13

2020-07-29

蘇 賢（1993—），男，福建省漳州市人，碩士，助理工程師，主要研究方向為電力系統傳感設備磁滯建模。