電纜故障點定位中小波分析應用的研究
沈陽工程學院 張家航 王存旭
電力電纜線路在供電過程中,尤其是在輸電配電環節,一直起著無可替代的作用。如何在電纜發生故障時及時、準確地發現故障并檢測出故障點的位置,是電纜發生故障時及時修復故障的關鍵。因此,為了滿足電力系統和用戶對供電可靠性的要求,及時修復電纜故障是非常必要的。對比于傅里葉變換,小波分析最大的優點在于它能同時解決小波信號在時域和頻域中傅里葉無法解決的兩個局部特征。因此,在電纜故障檢測過程中,可以利用matlab建立模型,然后對故障行波進行小波分解、處理和重構,確定電纜故障的具體位置。本文主要歸納了小波分析的基本理論思想,分析了小波分析在電力線路故障診斷中的幾種實際應用。通過理論分析,明確了應用小波進行電纜故障信號去噪理論的適用性。
1 小波分析基本理論
如果ψ∈L2(R)滿足允許性條件:

2 小波分析在電纜故障診斷中的應用
2.1 基于小波分析的電纜故障選線
在大型輸變電系統中,同一母線可能有多回出線。為了充分滿足大型電力系統在供電運行過程中對于經濟性的要求,安裝的行波線路故障信號測距裝置必須能夠同時監測多回輸電線路。當電力線路發生故障之后,每一回電力線路的行波啟動元件都存在著啟動的可能性,因此在發生電力電纜線路故障時,進行準確無誤的故障選線是十分必要的。基于幅值考慮,一般來說,正常電力線路的行波信號只包含一個透射分量。在實際操作中進行電力系統故障線路選線的主要依據為:正常情況下電力系統的輸電線路經過小波分析后,輸電線路行波信號的模極大值會呈現出下降趨勢,而輸電線路一旦發生故障,這一回輸電線路的行波信號經過小波變化的模極大值會變大,工作人員可通過對模極大值進行比較來對輸電線路進行故障選線,模極大值最大的線路即為故障線路。
2.2 基于小波分析的電纜故障信號奇異性檢測的研究
實驗分析過程中獲取一有明顯拐點的信號,通過選用恰當的小波對這一階躍信號進行多層分解可得到信號的突變點時刻,以此來驗證小波變換在電纜故障情形中應用的適用性。細節信號如圖1所示。

圖1 細節信號
從圖1中可以得出,在小波分解得到的細節信號波形中在t=100處有一個明顯的階躍變化,它是一個典型的階躍信號。因此,電力線路故障信號經過小波的多尺度分析之后獲得的結果可用來進行電力電纜故障信號奇異點的研究。電力電纜線路的故障信號經過多尺度小波分析后得到的結果具有模極大值。可根據模極大值推算出電力故障信號波形的奇異點。因此,將小波分析應用于電纜故障線路反射信號的奇異點檢測可用來明確電力電纜的發生故障的初始時刻以及判斷出故障點的位置所在。
2.3 基于傳統小波閾值規則的電纜故障波形去噪研究
小波變換消除電纜故障信號噪聲干擾的關鍵是閾值的選擇,選擇合適的閾值對消除典型電纜故障噪聲具有重要意義。下面給出兩種在分析中常見的閾值規則。
(1)Stein無偏似然估計閾值T1(rigrsure規則)
設一向量W=[w1,w2, ...,wn],且w1≤w2≤ ... ≤wn,n的含義同上。再設風險向量R,其元素為:
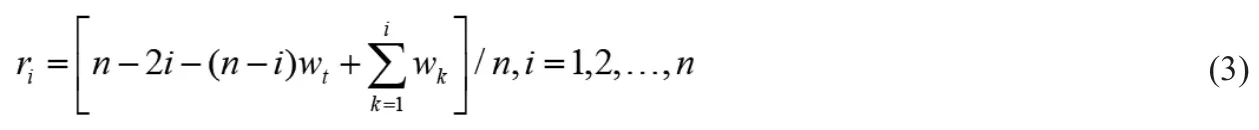
將R中的最小元素rb設為風險值,通過b能夠推算向量W對應的wb,閾值wb可表示為:

(2)最大最小準則閾值T2(minimax規則):
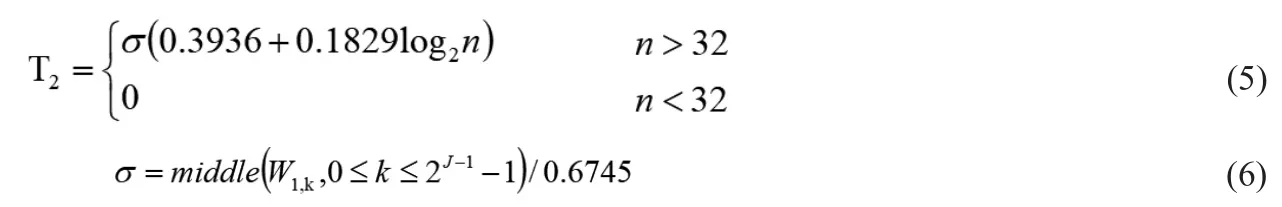
上述公式中,σ為噪聲信號的標準差,n為噪聲信號系數個數總和,W1,k為尺度等于1的小波系數。
含噪波形是原始波形加入白噪聲獲得,該原始信號具備較多的信號干擾,原始含噪波形經過最大最小準則閾值分析處理后可達到圖2所示去噪效果,經過分析可知該方法對電纜故障反射波形的去噪效果良好,有明顯的消噪效果。但如果想達到更高的精密度還需要在原有算法的基礎上做進一步的改進研究。
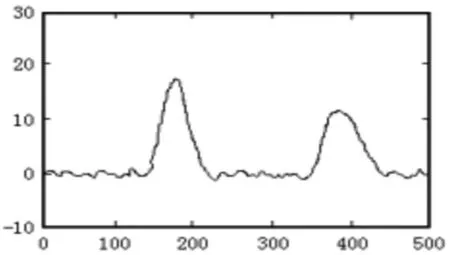
圖2 最大最小準則閾值去噪效果波形
3 結語
本文主要針對小波分析在電力電纜故障診斷中幾種常見的應用情形,研究了小波變換在這幾種電纜故障檢測實例中應用的適用性,包括電力電纜故障線檢測、電力電纜故障信號的奇異性檢測和含噪聲反射波形的噪聲消除等。電力電纜故障行波信號經過小波分析處理后獲得的奇異點往往攜帶著可用于電力線路故障檢測的重要信息。精準定位電力電纜故障點位置所在的關鍵在于檢測出電纜行波信號的奇異點與模極大值這兩個主要特征,而小波變換所具有的時頻局部化的特性剛好可用來檢測這兩個用來檢測電力線路故障的特征值。因此,小波變換在電纜故障診斷方面得到了很好的應用,但任然存在一些不足之處。如何完善這些不足之處是未來工作的重點。

