航空網(wǎng)絡(luò)關(guān)鍵節(jié)點(diǎn)辨識的核極限學(xué)習(xí)機(jī)算法研究

牛軍鋒，甘旭升，孫靜娟，涂從良

(1.西京學(xué)院 管理技術(shù)系, 西安 710123) (2.空軍工程大學(xué) 空管領(lǐng)航學(xué)院, 西安 710051)

0 引 言

隨著國際國內(nèi)機(jī)場、航路航線數(shù)量的指數(shù)式爆炸增長，以城市機(jī)場為節(jié)點(diǎn)、航線為連邊的航空網(wǎng)絡(luò)逐漸形成。航空網(wǎng)絡(luò)的發(fā)展水平反映了國家的社會和經(jīng)濟(jì)狀況，是國家實(shí)力的一種象征。在平時，航空網(wǎng)絡(luò)為社會各產(chǎn)業(yè)提供了交流和輸出平臺，促進(jìn)了經(jīng)濟(jì)發(fā)展。在戰(zhàn)時，航空網(wǎng)絡(luò)擔(dān)負(fù)著戰(zhàn)斗物資轉(zhuǎn)移與戰(zhàn)斗支援任務(wù)，直接影響戰(zhàn)爭進(jìn)程。

當(dāng)前，辨識航空網(wǎng)絡(luò)關(guān)鍵節(jié)點(diǎn)的理論研究已成為熱點(diǎn)。以往的關(guān)鍵節(jié)點(diǎn)辨識方法存在的不足主要體現(xiàn)在兩個方面：其一，重視網(wǎng)絡(luò)拓?fù)湫再|(zhì)及其節(jié)點(diǎn)相互關(guān)系，沒有考量網(wǎng)絡(luò)邊權(quán)。例如，H.W.Corley等通過研究刪除節(jié)點(diǎn)后的最短路徑來評估刪除節(jié)點(diǎn)的重要性；D.Gomezb等比較了接近中心性、介數(shù)中心性和度數(shù)中心性指標(biāo)，并引入博弈論評估了網(wǎng)絡(luò)節(jié)點(diǎn)的重要性；He Nan等根據(jù)節(jié)點(diǎn)度、效率研究了復(fù)雜網(wǎng)絡(luò)節(jié)點(diǎn)的重要排序問題；譚躍進(jìn)等在定義凝聚度基礎(chǔ)上提出了一種評估節(jié)點(diǎn)重要度的節(jié)點(diǎn)收縮方法，將收縮后網(wǎng)絡(luò)凝聚度最大的節(jié)點(diǎn)視為最重要的節(jié)點(diǎn)。上述研究主要適用于不帶權(quán)網(wǎng)絡(luò)，但基本沒有考慮航空網(wǎng)絡(luò)中航線流量的影響。其二，方法過于單一，一般僅考慮節(jié)點(diǎn)的某一性質(zhì)。例如，謝鳳宏等根據(jù)復(fù)雜網(wǎng)絡(luò)關(guān)鍵節(jié)點(diǎn)辨識算法的缺點(diǎn)，提出了一種基于加權(quán)聚類系數(shù)的復(fù)雜網(wǎng)絡(luò)節(jié)點(diǎn)重要度排序方法；Chen Duanbing等根據(jù)每種中心性度量自身缺點(diǎn)，將幾種不同的中心性度量多屬性化，并采用層次分析法對多屬性進(jìn)行聚合，得到各節(jié)點(diǎn)的影響評估值；王建偉等依據(jù)網(wǎng)絡(luò)中節(jié)點(diǎn)的局域特征，提出了一種基于近鄰節(jié)點(diǎn)度節(jié)點(diǎn)重要性的度量方法。上述研究簡便高效，不足之處是機(jī)場節(jié)點(diǎn)的重要性影響因素十分復(fù)雜，僅考慮個別性質(zhì)往往難以獲得準(zhǔn)確結(jié)論。

通常采用接近中心度、介數(shù)、網(wǎng)絡(luò)連接密度以及網(wǎng)絡(luò)效率來綜合評估節(jié)點(diǎn)的重要性。然而在實(shí)際計算中，上述指標(biāo)通常涉及最短路徑等復(fù)雜度高的運(yùn)算，導(dǎo)致評估過程耗時過長，進(jìn)而影響關(guān)鍵節(jié)點(diǎn)的辨識效果。因此，本文以節(jié)點(diǎn)度值、點(diǎn)強(qiáng)和

K

-shell值等簡單指標(biāo)作為輸入，以由復(fù)雜指標(biāo)得到的綜合重要度作為輸出，選取少量節(jié)點(diǎn)訓(xùn)練改進(jìn)型極限學(xué)習(xí)機(jī)(Extreme Learning Machine，簡稱ELM)模型，對航空網(wǎng)絡(luò)關(guān)鍵節(jié)點(diǎn)進(jìn)行辨識，并以中美兩國航空網(wǎng)絡(luò)為例進(jìn)行仿真驗(yàn)證。

1 節(jié)點(diǎn)簡單指標(biāo)

航空網(wǎng)絡(luò)對關(guān)鍵機(jī)場的研究主要是指標(biāo)分析，指標(biāo)較少時評估準(zhǔn)確度不夠理想，指標(biāo)較全面時計算的時間復(fù)雜度又很高。

簡單指標(biāo)值為訓(xùn)練知識數(shù)據(jù)庫，本文選取節(jié)點(diǎn)度值、點(diǎn)強(qiáng)、

K

-shell值作為簡單指標(biāo)。

節(jié)點(diǎn)度值：反映網(wǎng)絡(luò)中單個節(jié)點(diǎn)與相鄰節(jié)點(diǎn)間連接次數(shù)的指標(biāo)，定義為節(jié)點(diǎn)的直接連邊數(shù)。

(1)

式中：

a

為兩節(jié)點(diǎn)間的連邊狀況。若節(jié)點(diǎn)

v

和

v

不存在直接連邊，則

a

=0；否則，

a

=1。點(diǎn)強(qiáng)：主要指航空網(wǎng)絡(luò)中的邊權(quán)，即航線流量。點(diǎn)強(qiáng)

S

的表達(dá)式為

(2)

式中：

w

為與節(jié)點(diǎn)

v

直接連邊的權(quán)值；

N

為節(jié)點(diǎn)

v

的相鄰節(jié)點(diǎn)集合。

周圍機(jī)場與該機(jī)場節(jié)點(diǎn)聯(lián)系越緊密，連邊權(quán)值就越大。

K

-shell：

K

-shell法是節(jié)點(diǎn)排序的代表性算法，根據(jù)節(jié)點(diǎn)度或其他指標(biāo)，將處在網(wǎng)絡(luò)外殼的節(jié)點(diǎn)一層一層剝離，剝離越晚的節(jié)點(diǎn)就越重要，如圖1所示。其具體步驟是：搜索網(wǎng)絡(luò)中度為1的節(jié)點(diǎn)，刪除此類節(jié)點(diǎn)及其連邊；刪掉這些節(jié)點(diǎn)后，網(wǎng)絡(luò)結(jié)構(gòu)出現(xiàn)變化，將此時度是1的節(jié)點(diǎn)及其連邊刪除，依此過程，繼續(xù)刪除節(jié)點(diǎn)，直至網(wǎng)絡(luò)中不包含度為1的節(jié)點(diǎn)。將刪掉的節(jié)點(diǎn)組成的殼作為1-殼(即

Ks

=1)。同理，繼續(xù)去除節(jié)點(diǎn)度為2的節(jié)點(diǎn)，作為2-殼，以此類推，直至刪完所有節(jié)點(diǎn)。這種方法對節(jié)點(diǎn)進(jìn)行的是粗粒化排序，雖然精度不高，但反映了節(jié)點(diǎn)的全局性質(zhì)。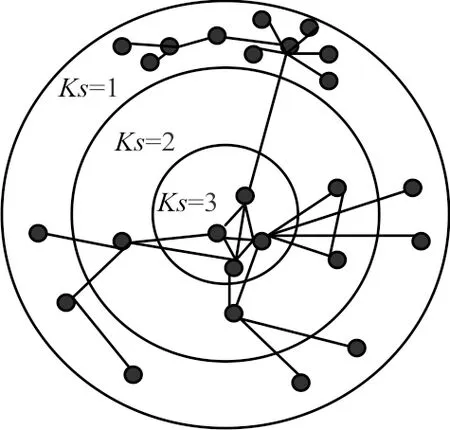

圖1 K-shell方法示意

對于節(jié)點(diǎn)

v

，其

K

-shell值為

Ks

，該值越大，節(jié)點(diǎn)越重要。簡單指標(biāo)的優(yōu)缺點(diǎn)對比如表1所示，這三個指標(biāo)比較有代表性，且都具有較低時間復(fù)雜度。

表1 三個簡單指標(biāo)的相關(guān)信息

對簡單指標(biāo)進(jìn)行歸一化：

對于節(jié)點(diǎn)

v

的度值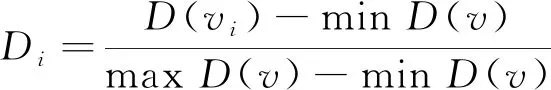

(3)

對于節(jié)點(diǎn)

v

的點(diǎn)強(qiáng)

S

和

K

-shell值

Ks

，做同樣的處理。綜上所述，

n

個節(jié)點(diǎn)可以組成一個簡單的指標(biāo)值矩陣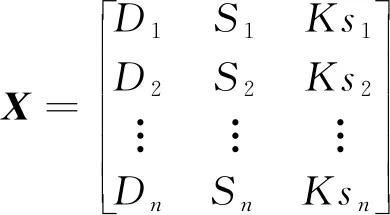

(4)

式中：為

n

個節(jié)點(diǎn)的度值、點(diǎn)強(qiáng)和

K

-shell值矩陣。

2 節(jié)點(diǎn)復(fù)雜指標(biāo)

在復(fù)雜網(wǎng)絡(luò)領(lǐng)域，辨識關(guān)鍵節(jié)點(diǎn)的方法主要包括社會網(wǎng)絡(luò)分析方法和系統(tǒng)科學(xué)分析方法。

對于社會網(wǎng)絡(luò)分析方法，可選取接近中心性與介數(shù)中心性作為評估指標(biāo)。

接近中心性(

CC

)：計算網(wǎng)絡(luò)中節(jié)點(diǎn)

v

與剩余節(jié)點(diǎn)的距離平均值，解決特殊值問題。若

v

與其他節(jié)點(diǎn)的距離比節(jié)點(diǎn)

v

小，則認(rèn)為

v

的

CC

比

v

大。通常，最靠近中心的節(jié)點(diǎn)具有信息流的最佳視野。設(shè)網(wǎng)絡(luò)包含

n

個節(jié)點(diǎn)，則

v

到網(wǎng)絡(luò)中剩余節(jié)點(diǎn)的最短距離平均值：

(5)

若

d

較小，則說明

v

比較接近網(wǎng)絡(luò)的剩余節(jié)點(diǎn)。

d

的倒數(shù)可定義為節(jié)點(diǎn)

v

的

CC

：

(6)

CC

(

i

)越大，

v

越接近網(wǎng)絡(luò)中心，位置越重要，重要性也越大。節(jié)點(diǎn)度和接近度方法效果對比如圖2所示，可以看出：接近度比節(jié)點(diǎn)度更能精確區(qū)分節(jié)點(diǎn)重要性。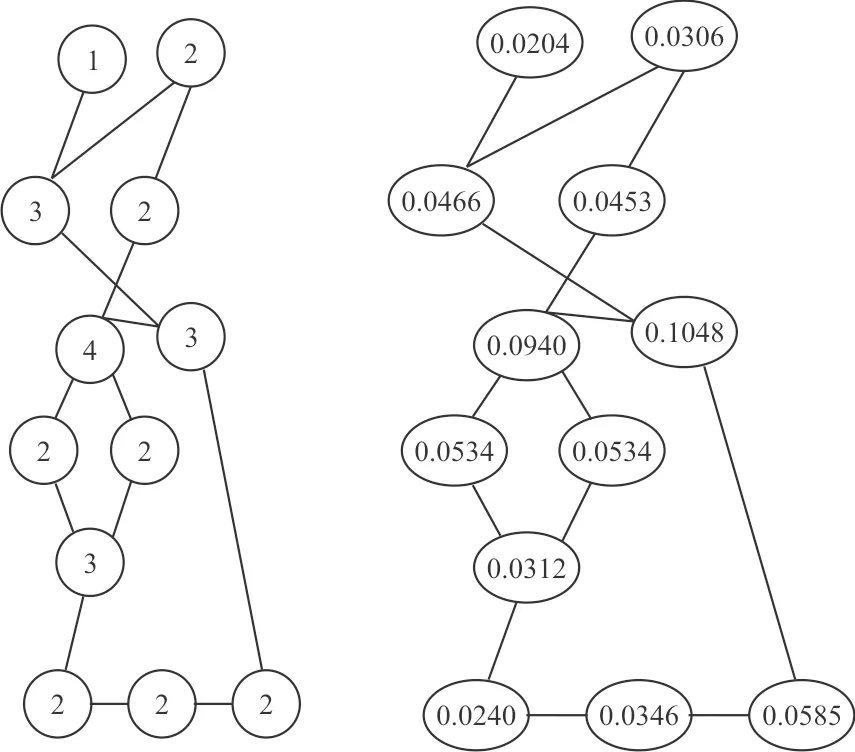

(a) 節(jié)點(diǎn)度 (b)接近度

介數(shù)中心性(

BC

)：在整體網(wǎng)絡(luò)中反映節(jié)點(diǎn)的中心程度，節(jié)點(diǎn)

v

的介數(shù)

BC

(

k

)是指經(jīng)過節(jié)點(diǎn)

v

的網(wǎng)絡(luò)中全部節(jié)點(diǎn)對間的最短路徑數(shù)占總最短路徑數(shù)的比重。

(7)

式中：

σ

(

k

)為

v

與

v

間經(jīng)由

v

的最短路徑數(shù)目；

σ

為

v

與

v

間最短路徑的數(shù)目。

對于系統(tǒng)科學(xué)分析方法，可采用節(jié)點(diǎn)刪除法。節(jié)點(diǎn)刪除法的思想是，刪除某個節(jié)點(diǎn)后，計算網(wǎng)絡(luò)性能，并與原網(wǎng)絡(luò)比較，網(wǎng)絡(luò)性能變化越大，節(jié)點(diǎn)就越重要。對于網(wǎng)絡(luò)性能，采用網(wǎng)絡(luò)連接密度與網(wǎng)絡(luò)效率來衡量。

網(wǎng)絡(luò)連接密度(

LD

)：在無權(quán)網(wǎng)絡(luò)中，連接密度指網(wǎng)絡(luò)中現(xiàn)有連邊與可能存在的連邊的比值。對于航空網(wǎng)絡(luò)，可定義加權(quán)連接密度：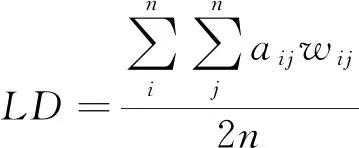

(8)

式中：

n

為當(dāng)前網(wǎng)絡(luò)節(jié)點(diǎn)總數(shù)；若

v

與

v

直接相連，

a

=1，否則，

a

=0；

w

為節(jié)點(diǎn)連邊的權(quán)值。

LD

越大，整體的異質(zhì)性越高，網(wǎng)絡(luò)流量越大，網(wǎng)絡(luò)綜合性能越好。網(wǎng)絡(luò)效率(

NE

)為所有節(jié)點(diǎn)之間的距離倒數(shù)和的平均值。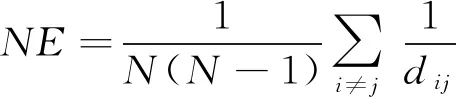

(9)

式中：

N

為網(wǎng)絡(luò)中節(jié)點(diǎn)總數(shù)。

NE

反映了網(wǎng)絡(luò)信息傳輸?shù)碾y易程度，

NE

越大，信息傳遞越順暢，抗毀性越強(qiáng)。

四個復(fù)雜指標(biāo)的優(yōu)缺點(diǎn)與時間復(fù)雜度對比如表2所示。

表2 四個復(fù)雜指標(biāo)的相關(guān)信息

從表2可以看出：除了連接密度外，其余三個指標(biāo)的計算時間復(fù)雜度均為

O

(

N

)。雖然綜合上述四個指標(biāo)能夠較為全面地反映節(jié)點(diǎn)的重要性，但這樣耗費(fèi)時間較長，不適合復(fù)雜的大型網(wǎng)絡(luò)。

3 核極限學(xué)習(xí)機(jī)(KELM)

考慮到航空網(wǎng)絡(luò)節(jié)點(diǎn)訓(xùn)練樣本集的復(fù)雜指標(biāo)計算復(fù)雜度較高，提出采用基于核函數(shù)的ELM (Kernel ELM,簡稱KELM) 來學(xué)習(xí)簡單指標(biāo)與綜合重要度之間的映射關(guān)系，以期耗費(fèi)較少的計算時間和資源，實(shí)現(xiàn)航空網(wǎng)絡(luò)節(jié)點(diǎn)重要度的準(zhǔn)確評估，進(jìn)而辨識出關(guān)鍵節(jié)點(diǎn)。

3.1 核函數(shù)理論

對于模式識別問題，當(dāng)樣本在低維空間線性不可分時，可通過某非線性函數(shù)映射到高維特征空間，能夠?qū)崿F(xiàn)線性可分。核函數(shù)基本原理：通過某非線性函數(shù)，將輸入空間樣本映射到高維特征空間，在高維特征空間進(jìn)行數(shù)據(jù)的處理。其關(guān)鍵在于，引入核函數(shù)后，能夠?qū)⒏呔S特征空間的內(nèi)積運(yùn)算轉(zhuǎn)化為輸入空間內(nèi)的運(yùn)算。

設(shè)

x

與

x

為輸入空間中的樣本點(diǎn)，原始輸入空間到高維特征空間的映射函數(shù)為

Φ

，則核函數(shù)方法可描述為實(shí)現(xiàn)內(nèi)積變換(

x

·

x

)→

K

(

x

,

x

)= <

Φ

(

x

),

Φ

(

x

)>

(10)

式中：

K

(

x

,

x

)為核函數(shù)；<

Φ

(

x

),

Φ

(

x

)>為內(nèi)積。在式 (10) 中，輸入空間的核函數(shù)與高維特征空間的內(nèi)積是等價的，非線性變換函數(shù)

Φ

的內(nèi)積運(yùn)算較為復(fù)雜，而核函數(shù)

K

(

x

,

x

)的運(yùn)算則相對簡單，因此，為了降低運(yùn)算復(fù)雜性，可用輸入空間的核函數(shù)運(yùn)算替代高維特征空間的內(nèi)積運(yùn)算。此外，在使用核函數(shù)時，無需明確

Φ

的具體形式和參數(shù)，極大地方便了運(yùn)算。核函數(shù)的映射過程如圖3所示。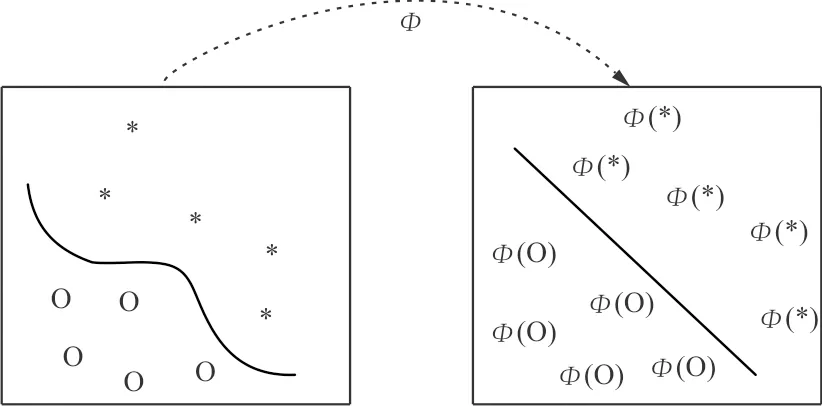

圖3 核函數(shù)的映射過程

3.2 基于核函數(shù)的ELM

(11)

則ELM的輸出函數(shù)為

(12)

對于訓(xùn)練樣本(,)，且=[

x

1,

x

2,…,

x

]∈

R

與=[

t

1,

t

2,…,

t

]∈

R

，

g

()為激勵函數(shù)，

L

為隱層節(jié)點(diǎn)個數(shù)(

L

≤

N

)。則ELM算法計算步驟：(1) 隨機(jī)初始化輸入層與隱層的權(quán)值向量和隱層節(jié)點(diǎn)偏置值

b

；(2) 構(gòu)建隱層輸出矩陣=[

g

(),…,

g

()]；

其中，=[

x

,

x

,…,

x

]，為

N

個樣本；

g

()表示ELM網(wǎng)絡(luò)隱層節(jié)點(diǎn)的輸出函數(shù)，根據(jù)核函數(shù)理論，通過非線性函數(shù)將輸入空間的樣本點(diǎn)映射入特征空間，并由核函數(shù)代替特征空間的內(nèi)積運(yùn)算。假設(shè)隱層特征映射函數(shù)

g

()形式未知，則可用核函數(shù)代替其內(nèi)積形式。ELM可通過核矩陣形式來描述

Ω

=∶

Ω

ELM,=

g

()·

g

()=

K

(,)

(13)

此時，基于核函數(shù)的ELM (KELM) 輸出函數(shù)為

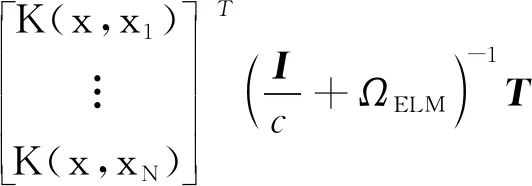
(14)

不難理解，在KELM算法中，無需了解

g

()的具體形式，僅需明確具體核函數(shù)

K

(,)，就可計算輸出函數(shù)的值。需要說明的是，核函數(shù)為內(nèi)積形式，在計算式 (12) 時，不需要確定網(wǎng)絡(luò)隱層節(jié)點(diǎn)的個數(shù)。

4 節(jié)點(diǎn)重要度評估流程

本文提出采用KELM對航空網(wǎng)絡(luò)節(jié)點(diǎn)重要度進(jìn)行評估的流程如圖4所示。

圖4 節(jié)點(diǎn)重要性評估流程

具體可劃分為以下四個步驟：

(1) 構(gòu)造訓(xùn)練樣本。從網(wǎng)絡(luò)中隨機(jī)生成部分節(jié)點(diǎn)，計算度值、點(diǎn)強(qiáng)和

K

-shell值等簡單節(jié)點(diǎn)指標(biāo)值；同時，確定接近中心性、介數(shù)中心性、網(wǎng)絡(luò)連接密度和網(wǎng)絡(luò)效率等復(fù)雜指標(biāo)值。(2) 確定綜合重要度。通過層次分析法(AHP)計算得出各復(fù)雜指標(biāo)的權(quán)重：

W

=0.578 9;

W

=0.205 5;

W

=0.159 2;

W

=0.056 5，進(jìn)而通過公式

Y

=0.578 9

BC

+0.205 5

NE

+0.159 2

CC

+0.056 5

LD

計算以上隨機(jī)節(jié)點(diǎn)的綜合重要度=[

Y

,

Y

,…,

Y

]。(3) 訓(xùn)練評估模型。以為輸入，以為輸出，訓(xùn)練KELM評估模型，以學(xué)習(xí)其內(nèi)在關(guān)系。(4) 執(zhí)行評估過程。對于網(wǎng)絡(luò)中除訓(xùn)練樣本的新節(jié)點(diǎn)，僅需計算新節(jié)點(diǎn)的簡單指標(biāo)，并輸入KELM評估模型，就能計算出新節(jié)點(diǎn)的綜合重要度，進(jìn)而完成關(guān)鍵節(jié)點(diǎn)的辨識。此外，KELM訓(xùn)練時對參數(shù)變化反應(yīng)比較敏感，當(dāng)

c

值比較小，而

σ

值比較大時，模型的訓(xùn)練精度非常高，而測試精度卻不理想，說明此時參數(shù)對訓(xùn)練的數(shù)據(jù)擬合程度非常高，但對新樣本的預(yù)測能力卻非常低，即出現(xiàn)通常所說的“過學(xué)習(xí)”現(xiàn)象。因此，在選取參數(shù)

c

和參數(shù)

σ

時，可引入交叉驗(yàn)證思想，計算出測試精度較高時所對應(yīng)的最優(yōu)參數(shù)組合。

5 仿真分析

為了驗(yàn)證本文所提方法的可行性，首先對隨機(jī)網(wǎng)絡(luò)進(jìn)行測試，然后分別對中美兩國航空網(wǎng)絡(luò)進(jìn)行測試，并對測試結(jié)果進(jìn)行分析。

5.1 隨機(jī)網(wǎng)絡(luò)測試

考慮一隨機(jī)網(wǎng)絡(luò)

G

={

V

,

E

,

W

}，該網(wǎng)絡(luò)含有600個節(jié)點(diǎn)，6 000條連邊，實(shí)驗(yàn)?zāi)康氖菣z驗(yàn)KELM關(guān)鍵節(jié)點(diǎn)辨識方法的有效性，也即判斷KELM能夠準(zhǔn)確學(xué)習(xí)簡單指標(biāo)與綜合重要度之間的關(guān)系。按照關(guān)鍵節(jié)點(diǎn)識別算法步驟，先隨機(jī)選擇60個節(jié)點(diǎn)作為KELM訓(xùn)練樣本，通過AHP得出復(fù)雜指標(biāo)

CC

、

BC

、

LD

和

NE

的權(quán)重分別為0.159 2,0.578 9,0.056 5,0.205 5，計算復(fù)雜指標(biāo)加權(quán)，其和為綜合重要度值

Y

，然后計算對應(yīng)簡單指標(biāo)值

X

。KELM訓(xùn)練前，利用交叉驗(yàn)證法在log

c

∈[-10,10]與log

σ

∈[-10,10]內(nèi)自動搜索最佳的參數(shù)

c

和參數(shù)

σ

，參數(shù)尋優(yōu)過程如圖5所示。圖中，復(fù)雜指標(biāo)重要度的實(shí)際值和預(yù)測值的均方根誤差

RMSE

為

(15)

圖5 對隨機(jī)網(wǎng)絡(luò)的參數(shù)尋優(yōu)過程

從圖5可以看出：網(wǎng)格圖底部較平緩，說明在很大取值范圍內(nèi)的兩個參數(shù)都可以使

RMSE

最小，因此，能夠較容易地找出最佳參數(shù)

c

和

σ

。進(jìn)行訓(xùn)練后，隨機(jī)選擇除訓(xùn)練樣本之外的60個節(jié)點(diǎn)作為測試節(jié)點(diǎn)，計算得到其簡單指標(biāo)

X

，并輸入KELM重要度評估模型，得到測試結(jié)果

Y

，與其原來復(fù)雜指標(biāo)值評估得到的重要度

Y

進(jìn)行比較，效果如圖6所示。

圖6 測試結(jié)果與實(shí)際值對比(隨機(jī)網(wǎng)絡(luò))

從圖6可以看出：KELM輸出的結(jié)果與原來的重要度值非常接近，說明本文方法是準(zhǔn)確、可行的。由表2可知，使用復(fù)雜指標(biāo)對節(jié)點(diǎn)重要度評估所需時間復(fù)雜度為

O

(

N

)，而KELM評估僅需

O

(

N

)，其中，

N

為訓(xùn)練樣本數(shù)。因此，采用這種方法，可以通過簡單、耗時少的指標(biāo)快速得到節(jié)點(diǎn)的綜合重要度。

5.2 航空網(wǎng)絡(luò)測試

對于美國航空網(wǎng)絡(luò)，做同樣測試，實(shí)驗(yàn)數(shù)據(jù)集包含332個機(jī)場節(jié)點(diǎn)、2 126條連邊(直飛航線)以及連邊的權(quán)重，美國航空網(wǎng)絡(luò)的拓?fù)鋱D如圖7所示。數(shù)據(jù)來源詳見文獻(xiàn)[14]。

圖7 美國航空網(wǎng)絡(luò)拓?fù)?/p>

根據(jù)本文方法，通過交叉驗(yàn)證法確定參數(shù)，如圖8所示。在節(jié)點(diǎn)重要度評估過程中，耗時最長的是知識數(shù)據(jù)庫的建立(用復(fù)雜指標(biāo)評估節(jié)點(diǎn)重要度)，如果選擇網(wǎng)絡(luò)中大部分節(jié)點(diǎn)作為訓(xùn)練樣本，評估方法就失去了時間復(fù)雜度低的優(yōu)勢，變得沒有意義。因此，本文測試KELM是否僅需要很少一部分節(jié)點(diǎn)就能準(zhǔn)確評估節(jié)點(diǎn)重要度，分別隨機(jī)選擇20、40、60、80個節(jié)點(diǎn)作為訓(xùn)練樣本，然后比較測試結(jié)果與原來的重要度值，如圖9所示。

圖8 對美國航空網(wǎng)絡(luò)的參數(shù)尋優(yōu)過程

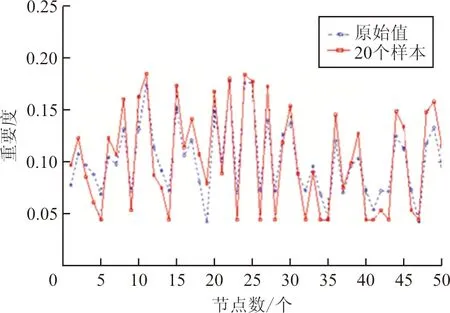
(a) 20個訓(xùn)練樣本

(b) 40個訓(xùn)練樣本

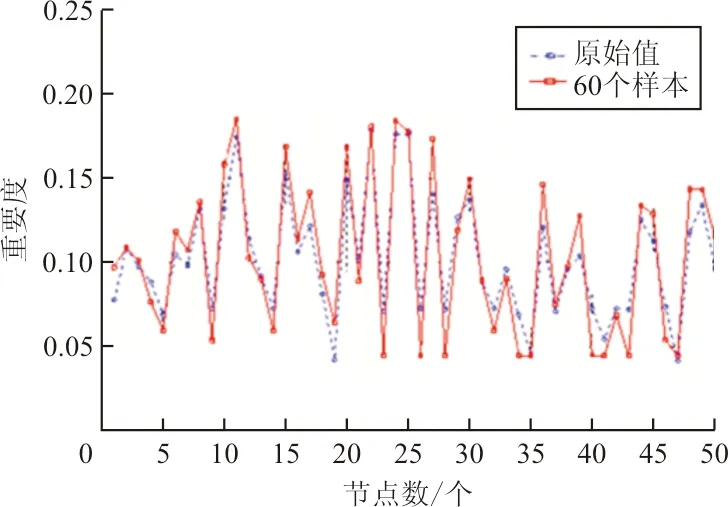
(c) 60個訓(xùn)練樣本

(d) 80個訓(xùn)練樣本

從圖9可看出：選擇20個訓(xùn)練樣本時，測試結(jié)果與原值的擬合效果較差，當(dāng)選擇40個訓(xùn)練樣本時，擬合效果明顯改善，選擇60、80個節(jié)點(diǎn)時，擬合效果無明顯提升。因此，在美國航空網(wǎng)絡(luò)中，僅需計算40個節(jié)點(diǎn)的復(fù)雜指標(biāo)值，如此將大幅降低原來的運(yùn)算量，提高辨識關(guān)鍵節(jié)點(diǎn)的效率。

選擇40個節(jié)點(diǎn)作為訓(xùn)練樣本，對所有節(jié)點(diǎn)進(jìn)行測試，得到測試結(jié)果后對節(jié)點(diǎn)進(jìn)行排序，并與原復(fù)雜指標(biāo)評估重要度排序、ACI排序進(jìn)行比較，如表3所示。其中，ACI指國際機(jī)場委員會對美國各機(jī)場的綜合排名。

表3 美國機(jī)場節(jié)點(diǎn)重要度排序

從表3可以看出：測試結(jié)果(簡單指標(biāo)評估結(jié)果)排名前16的機(jī)場節(jié)點(diǎn)與ACI僅有3個不同，說明本文方法比較符合現(xiàn)實(shí)情況，具有一定的準(zhǔn)確性。再將測試結(jié)果與復(fù)雜指標(biāo)評估結(jié)果作比較，發(fā)現(xiàn)兩種方法的結(jié)果幾乎一致，在前幾名中，只有San Francisco與G.Bush對調(diào)了順序，后幾名略有差異，說明KELM的學(xué)習(xí)效果較好，具有準(zhǔn)確預(yù)測數(shù)據(jù)的能力。

為了驗(yàn)證算法的通用性，把本文方法應(yīng)用于中國的航空網(wǎng)絡(luò)。將國內(nèi)2016年199個具有定期航班的通航城市作為目標(biāo)節(jié)點(diǎn)，爬取和收集網(wǎng)頁數(shù)據(jù)，構(gòu)建我國航空網(wǎng)絡(luò)模型，并對我國航空網(wǎng)絡(luò)進(jìn)行關(guān)鍵節(jié)點(diǎn)識別。參數(shù)尋優(yōu)過程如圖10所示，檢驗(yàn)測試結(jié)果的準(zhǔn)確性如圖11所示，可以看出：測試結(jié)果在趨勢上與實(shí)際值總體保持一致。

圖10 對中國航空網(wǎng)絡(luò)的參數(shù)尋優(yōu)過程

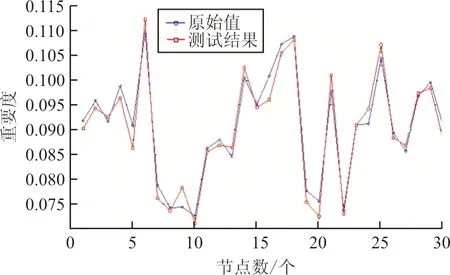
圖11 測試結(jié)果與原值對比(中國航空網(wǎng)絡(luò))

6 結(jié) 論

(1) 基于接近中心性、介數(shù)中心性、網(wǎng)絡(luò)連接密度對節(jié)點(diǎn)進(jìn)行綜合重要度評估，克服了以往復(fù)雜網(wǎng)絡(luò)研究領(lǐng)域未考慮航線流量、機(jī)場位置等影響節(jié)點(diǎn)重要性的航空網(wǎng)絡(luò)具體因素的不足。

(2) 采用KELM學(xué)習(xí)綜合重要度值與簡單指標(biāo)的映射關(guān)系。對于剩余大部分節(jié)點(diǎn)，只需求出其簡單指標(biāo)，便可以求得其綜合重要度和節(jié)點(diǎn)排序。解決了傳統(tǒng)指標(biāo)單一、未考慮邊權(quán)的問題，提高了節(jié)點(diǎn)排序的準(zhǔn)確性，同時降低了計算復(fù)雜度，節(jié)省了大量時間，實(shí)例驗(yàn)證了其有效性和可行性。

(3) 鑒于數(shù)據(jù)獲取和時間問題，本文僅研究了民用機(jī)場構(gòu)成的航空網(wǎng)絡(luò)，在未來的研究中可以繼續(xù)拓展，獲取更加充實(shí)的數(shù)據(jù)，構(gòu)建軍航或者軍民聯(lián)合航空網(wǎng)絡(luò)，以用于航空網(wǎng)絡(luò)的平戰(zhàn)轉(zhuǎn)換機(jī)制研究。