基于高分辨率遙感影像的花粒期玉米葉面積指數估算方法

任楓荻,陳圣波,陳彥冰

(吉林大學 地球探測科學與技術學院,吉林 長春 130026)

0 引言

葉面積指數(Leaf Area Index, LAI)反映單位土地面積上植物葉片的總面積,是反映作物群體特征的重要指標,是表征植被冠層結構和反映植被長勢的重要生理參數[1,2]。目前進行LAI測量的方法有直接法和間接法兩種。直接法是指使用儀器實地測量葉面積指數,結果較為準確,但是耗時耗力,并會造成葉片組織的損傷,且測量結果并不具有普遍代表性,因此,僅僅適用于部分地區的驗證性測量。間接法是指采用遙感手段進行大范圍的植被指數估算。遙感技術具有時空分辨率高、數據采集成本低以及可以實現大面積、寬領域、實時動態監測等優勢[3-4],為估算大范圍植被的LAI提供了有效的技術手段。

利用間接法獲取葉面積指數的模型方法分為經驗模型和物理模型兩類。經驗模型是以 LAI為因變量,以光譜數據或其變換形式(例如植被指數)作為自變量建立的估算模型,是目前國內外利用遙感技術來估算葉面積指數的主要方法[5]。隨著遙感衛星數據的普及,前人利用HJ衛星影像生成了HJVI、NDVI、EVI等7種數據,構造了夏玉米LAI的估算模型[6]。還有人采用GF-1和Landsat8遙感影像,開展了葉面積指數的估算研究[7]。根據遙感影像可以提取植被指數,建立植被指數與葉面積指數間的關系模型，從而估測LAI。有學者對比研究了10個常見植被指數與不同生育時期LAI的相關性及預測性,篩選出預測LAI的最佳植被指數和最優模型[8]。在眾多植被指數中，利用EVI建立的葉面積指數估算模型的精度優于同類植被指數模型[9]。對多種常見植被指數的估算效果進行簡單的回歸分析后得出,用EVI估算LAI是具有較高精度的[10]。物理模型法需要利用大量的物理參數模擬農作物的生長過程,適用性比較好,多應用于農作物物理數據豐富、參數齊全情況下的LAI建模。物理模型方法種類較多,利用PROSAL輻射傳輸模型[11]、建立神經網絡估算模型[12]、采用隨機森林算法[13]都可以準確估算所研究作物的LAI。但由于物理模型法需要測量作物的許多生理物理參數用作輸入,模型過于復雜,難以推廣應用。

目前遙感衛星影像具有高空間分辨率、高清晰度、信息量豐富及數據時效性強等優點,可以提供更多地物的細節信息,因此針對衛星數據的LAI估算模型優選和真實性檢驗日益得到重視[14]。前人對于估算玉米葉面積指數的研究多為整個玉米生長期的綜合研究,而單獨對某一時期針對性的研究較少,并且適于玉米不同生育期的葉面積指數估算模型應是不同的,鑒于此，我們主要對玉米花粒期的葉面積指數估算進行了研究。本研究基于吉林省中部地區玉米花粒期的多種植被指數與實測LAI數據,提取相關性較好的植被指數,進行線性和非線性相關分析,構建回歸分析模型,最終對模型進行了驗證分析,檢驗所建模型的適用性和可靠性。

1 研究區域和數據源

1.1 研究區域概況

本研究的5個實驗地區位于吉林省中部,其在吉林省的位置如圖1。吉林省平均每年日照時數為2259～3016 h,年平均降水量為400～600 mm,冬季平均氣溫在-11 ℃以下,夏季平原平均氣溫在23 ℃以上。吉林省具有優質的土壤和豐富的土地資源,光、熱、水分條件可以滿足作物生長需要,農作物以玉米為主。根據吉林省玉米生長時期和氣候條件,玉米于5月初播種,8月上旬進入玉米的花粒期,9月下旬逐步進入成熟期。

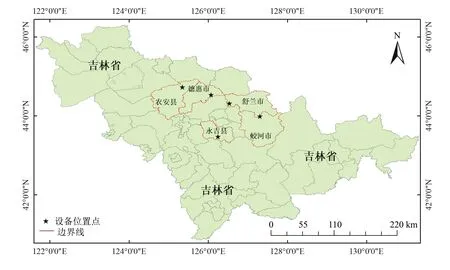
圖1 研究區的相對位置圖

1.2 影像數據源

本文所用的衛星遙感數據來自美國Planet Labs遙感衛星群, Planet Labs(PL)影像有藍(485 nm)、綠(545 nm)、紅(630 nm)、近紅外(820 nm)4個標準光譜波段,空間分辨率為3 m。本文采用的遙感影像數據對應地區和日期分別是蛟河市2019年9月11日、永吉縣2019年8月28日和2019年9月14日、舒蘭市2019年9月1日、德惠市2019年9月1日和2019年9月11日，以及農安縣2019年9月11日。

1.3 實測數據

本研究采用地面安裝的農情監測設備傳輸的數據,數據于2019年8月17日開始采集,于2019年9月17日結束采集。農情監測設備分布在5個實驗地區的玉米地塊內。該設備可在每1個樣點測量記錄作物的株高、冠層大小、葉片面積等物候信息,后期設備傳輸的數據計算出葉面積指數,作為該樣點的有效LAI值。同時利用GPS定位儀記錄每1個設備位置的經緯度。

2 研究方法

針對PL衛星遙感數據,應用ENV I5.3軟件計算出多種廣泛使用的植被指數,結合實驗地區玉米的地面實測LAI數據,利用SPSS Statistics 20軟件采用多種回歸模型進行LAI估算,對比不同模型的輸出結果,并分析不同模型的估算精度,最后篩選出最佳估算模型。

2.1 植被指數的選取

植被指數(Vegetation Index, VI)是用兩個或多個波長范圍內的地物反射率進行線性或非線性組合運算,產生某些對植被長勢、生物量等有一定指示意義的專題數值[15]。本文在建立LAI-VI關系時,為了探討不同因素對于估算LAI的影響,選取了比較常見且被廣泛使用的植被指數:增強植被指數EVI[16]、歸一化植被指數NDVI[17]、比值植被指數RVI[18]、優化土壤調節植被指數OSAVI[19]以及土壤調節植被指數SAVI[20],以LAI為因變量,以不同類型的植被指數為自變量,建立LAI估算回歸模型。

在進行回歸分析之前,首先在SPSS Statistics 20軟件中依次分析選取的植被指數與LAI之間的相關關系。依據統計學中的相關規定,當相關系數的絕對值在0.6～0.8時為強相關。本文分析了各類植被指數與實測葉面積指數間的相關性。由表1可知,玉米的LAI與各植被指數間的相關系數均高于0.6,說明這幾種植被指數均與LAI呈強相關,其中EVI與LAI的相關性最強,SAVI與LAI的相關性較強，因此本文只選取增強植被指數EVI和土壤調節植被指數SAVI進行研究。選取的植被指數對玉米LAI的變化較靈敏,適合構建經驗回歸模型。其中,EVI對基礎數據進行了全面的大氣校正,并對土壤背景的影響作了處理,因此它是綜合處理土壤、大氣、飽和問題的植被指數,是對NDVI的繼承和改進。另一植被指數SAVI的提出主要是用來減少植被指數對不同土壤反射變化的敏感性,有效地降低了土壤背景的影響,改善了植被指數與葉面積指數間的關系。

表1 植被指數與LAI間的相關系數

2.2 植被指數回歸模型的構建

將玉米實測LAI與EVI和SAVI這2種植被指數進行相關分析后,分別應用線性、對數、二次曲線、冪函數、S曲線以及指數形式模型與對應的LAI進行回歸擬合,利用判定系數R2篩選出擬合LAI精度最高的回歸模型。判定系數的結果如表2所示。

表2 不同回歸模型的判定系數

從表2中可以看出：兩種植被指數作自變量時擬合效果最好的模型均是二次曲線模型,其次是線性模型；兩種植被指數相對比，采用以SAVI作自變量的二次曲線模型的擬合效果又優于以EVI作自變量的二次曲線模型。所以在這6種模型中，玉米LAI擬合效果最佳的回歸模型是以SAVI作自變量的二次曲線模型。各植被指數最優的回歸方程如圖2所示。

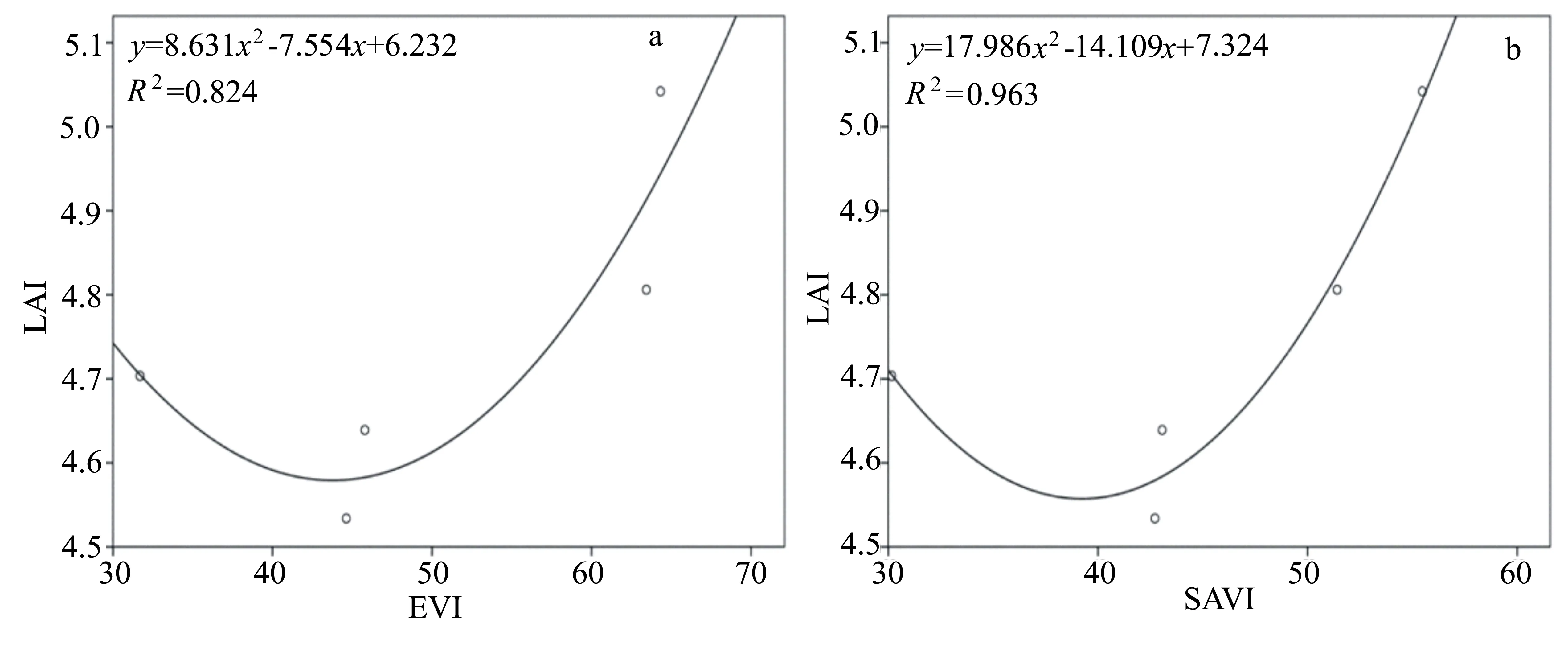
a為EVI估算的最佳回歸方程。b為SAVI估算的最佳回歸方程。

3 結果與分析

由表2可以看出，在LAI-VI二次曲線回歸模型建立中,二次曲線回歸模型的R2都大于0.5,具有較好的擬合效果。本文選取5個實測的玉米LAI數據作為回歸模型的建模樣本,用剩余的兩個數據作為驗證數據,并利用最優回歸模型計算出樣本點的估測LAI值。

3.1 模型估算結果

用于驗證的兩個LAI數據分別為4.476和4.524。對第1個驗證數據，利用EVI建立的模型估測的LAI值為4.581,用SAVI建立的模型估測的LAI值為4.565;對第2個驗證數據，利用EVI建立的模型估測的LAI值為4.680,用SAVI建立的模型估測的LAI值為4.647。說明用SAVI估算的玉米LAI值比其他植被指數的估算結果更加接近于地面實測的LAI值。

3.2 精度驗證結果

本文采用均方根誤差(Root Mean Square Error，RMSE)和相對誤差(Relative Error，RE)這兩個指標對所建立的回歸模型進行精度驗證。其中RMSE是衡量觀測值與真實值之間的偏差,常用來作為模型預測結果衡量的標準。而RE指測量所造成的絕對誤差與被測量真值之比乘以100%所得的數值,以百分數表示。一般來說,RE更能反映測量的可信程度。

精度驗證結果:以EVI建立的回歸模型驗證的RMSE為0.133,RE為2.896%;基于SAVI回歸模型驗證的RMSE為0.107,RE為2.352%。在物理意義上當RE小于5%時證明所建模型的估測精度較高，因此這兩個模型的估測精度均較高。各植被指數模型的RMSE值都小于0.3,說明各模型的估測精度均較高,其中SAVI模型的RMSE最低,只有0.107,故此模型的估測效果最好。因此,在吉林省中部的這5個地區可以利用SAVI植被指數所建立的二次曲線回歸模型來估算花粒期玉米的葉面積指數。

4 小結與討論

本次研究以吉林省中部5個地區為研究區,選取5種常用植被指數進行分析,根據相關系數篩選相關性較好的兩種植被指數SAVI和EVI,分別建立6種線性與非線性統計回歸模型,最終利用判定系數指標來選取估算葉面積指數的最優回歸模型。結果表明,擬合精度最高的模型是以SAVI為自變量的二次曲線回歸模型,其估算值與地面實測值較為一致,這進一步為農作物遙感理論研究和應用提供了理論依據。本研究結果如下：5種常用植被指數與LAI間的相關系數均大于0.6,其中SAVI和EVI與LAI間的相關系數居前2位；在以SAVI和EVI這2個植被指數作自變量所建立的12種模型中，采用以SAVI作自變量的二次曲線模型估算花粒期玉米葉面積指數的效果最佳，其方程式為y=17.986x2-14.109x+7.324,相關系數為0.728,相對誤差為2.352%,均方根誤差為0.107，其擬合精度和適用性較強,可用于獲取高精度的玉米LAI信息。