局部圍線積分雙譜的雷達信號源指紋識別技術

江西工業職業技術學院 龔再蘭

在處理和分析非最小相位系統、非高斯過程和非線性系統的一種重要方法是雙譜分析法，雙譜的重要特征是高階譜能夠反映出其信號的相位信息，除了線性相位以外，雙譜包含了全部的信號信息，且雙譜分析法中雷達信號的雙譜具有平移不變性，因此雙譜分析法有效的應用在雷達信號源指紋特征提取中。雖然雙譜在理論可以完全抑制任何對稱分布的非高斯噪聲和高斯噪聲，但是直接應用雙譜分析作為識別雷達信號源的特征向量，不僅有很大的信息冗余，而且還需要有足夠大的目標模板庫。

為了減少雙譜的數據量，以達到減少目標模板庫存儲量和信息冗余以達到實時處理信息的目標，本文提出了局部圍線積分雙譜的輻射源個體識別的方法，即利用雙譜分析雙譜估計值中具有最強鑒別能力的部分雙譜估計值，對輻射源個體特征參數進行提取、優化，作為輻射源分類識別的特征向量，并用重構核函數的支持向量機完成識別三部不同雷達信號源個體的信號。實驗結果表明，該方法具有較高的識別率。

1 局部圍線積分雙譜及二次特征提取

1.1 局部圍線積分

在區分M個雷達信號源時，每個雷達信號源發射信號可記為{N1,N2,...,NM}，圍線積分雙譜定義式為：

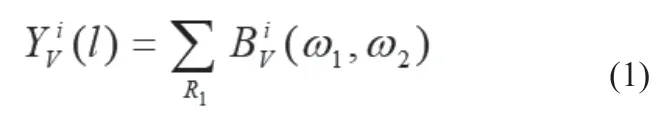
式(1)中，i=1, 2,...,M為雷達信號源數目，v=1, 2,...,Ni為捕獲的信號數據組數，Rl(l=1, 2,...,L)為圍線雙譜積分路線。鑒別函數表達式為：

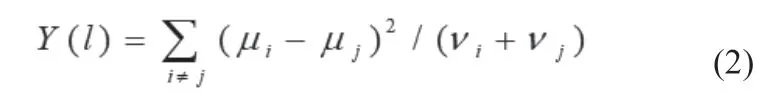
式(2)中，μi、μj為第i、j類信號積分雙譜的平均值，vi、vj為信號的積分雙譜的方差。局部圍線積分雙譜法，即在圍線積分雙譜中利用鑒別函數Y(l)來篩選出相對大的參數值，把篩選出來的參數值重新組合成一維矩陣數組。

1.2 二次特征值提取

在局部圍線積分雙譜重新組合成的一維矩陣數組的基礎上提取特征值，因為雙譜的奇異值具有穩定性、轉置不變性和位移不變性，因此，在雷達信號源的信號識別過程中把雙譜的奇異值作為識別和分類的特征向量。為了不遺漏或不丟失有用的奇異值信息，并且最大限度降低特征向量的維數，本文利用信息熵理論，二次特征提取雙譜的奇異值熵、能量熵和波形熵。

2 重構核函數

本文在支持向量機解決兩類分類問題的基礎上，衍生出支持向量機一對多的設計理念，即進行有M類信號時，就需要M個判決函數。分類判決的優劣在于判決函數中核函數的選取，因為核函數的選擇不同就會識別出不同的分類效果。為了解決提高分類識別率的問題，本文有機的融合了兩種核函數的優點，采用了由多項式核函數和高斯徑向核函數線性相關的重構核函數，重構核函數的設計理念找到最優的線性參數值，即篩選出最優核函數，其表達式可寫為：

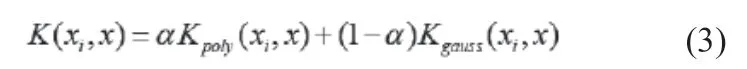
式(3)α∈(0, 1)。由實驗經驗值可知，Kpoly(xi,x)中的參數q和Kgauss(xi,x)中的參數δ，構成最優核函數的參數值為重構權重系數α = 0.98、q= 2和δ = 0.6。

3 分類器的設計

在分類器的設計過程中，可分為兩個步驟：訓練樣本庫和測試樣本庫。

第一步，訓練王本庫。針對M類雷達源信號分類器設計，本文采用逐次分類法的原理，即在訓練第N類的分類器時，把屬于第N類的訓練樣本記為I類，其余所有其他類的樣本都標記為II類，根據重構核函數由支持向量機解出第N類的判決函數fN(xN, X)，依次類推，直到訓練出M個判決函數即M個分類器為止。對于每一類的類心，采用樣本的質心代表，由支持向量機訓練后得到的判決函數集為{f1(x1,x),f2(x2,x),...,fM(xM,x)}。

第二步，測試樣本庫。把測試樣本x代入到各類已經訓練完成的判決函數集，輸出最大值的判決函數所對應的類別即為測試樣本的所屬類別。

4 實驗數據分析及結果

實驗分別采集由Agilent83752A信號源、Agilent E4438信號源和Anritsu MG3694B信號源發射的CW信號，并用Agilent型號為DSO6032A的示波器采集數據。CW信號的參數設置：載頻分別為20MHz、40MHz、80MHz、100MHz、200MHz，采樣頻率為1GHz，每個載頻采集六組實測數據，每組采樣點數為1000個，重復周期為15μs，發射功率為6dBm，發射的脈沖寬度為1μs。為了能更突出地體現本文技術的優勢，實驗數據分別利用圍線積分特征值提取及識別和局部圍線積分特征值提取及識別進行對比。

4.1 圍線積分特征值提取及識別

對所采集的數據的雙譜值進行圍線積分特征值提取，得到能量熵En，波形熵Eb，奇異值熵Es，利用重構核函數支持向量機，分類識別時以二維特征向量[Es，En]、[Es，Eb]、[Eb，En]識別參數。

圖2和圖3是載頻為100MHz時利用圍線積分法二維特征向量的識別結果。

表1為實載頻分別為20MHz、40MHz、80MHz、100MHz、200MHz時，圍線積分法進行分類識別率。由圖1、圖2、圖3分類結果和表1可以看出，圍線積分雙譜法的分類識別率隨著載頻的增加而有所降低。

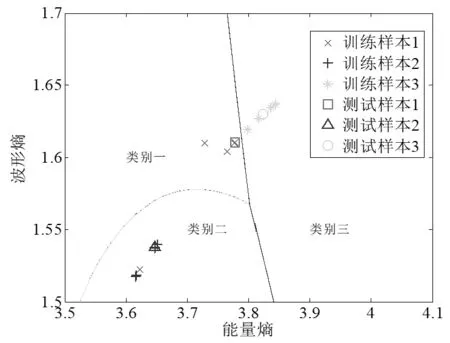
圖1 En和Eb組成的二維特征向量的識別

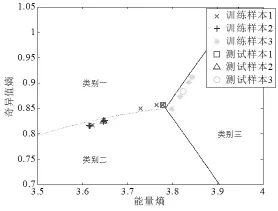
圖2 En和Es組成的二維特征向量的識別

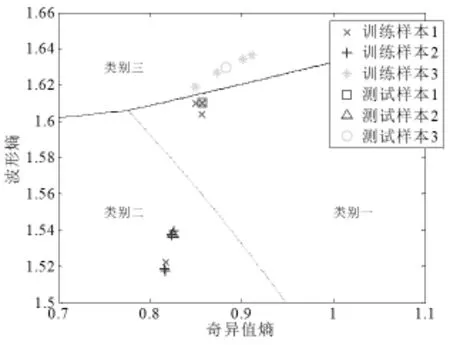
圖3 Es和Eb組成的二維特征向量的識別

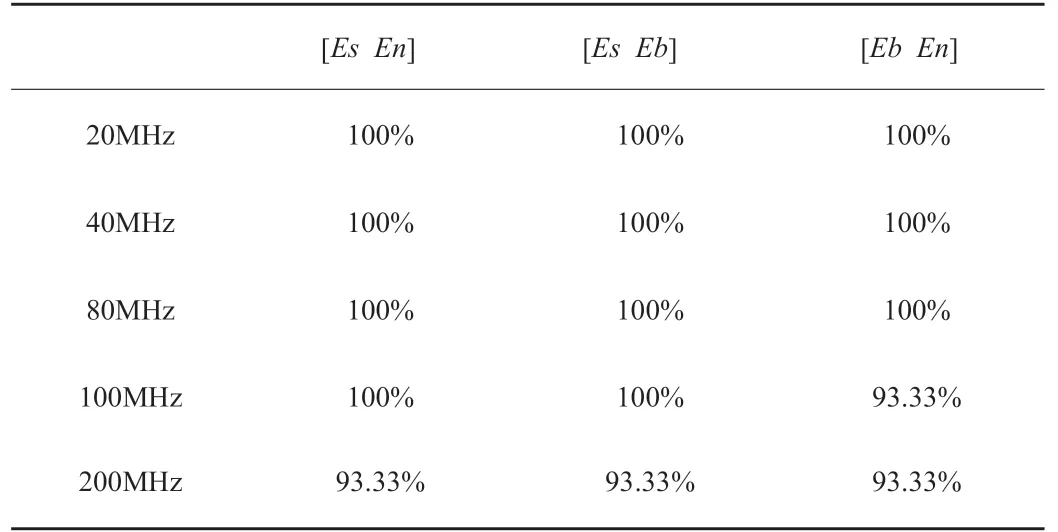
表1 圍線積分法分類識別率匯總表

4.2 局部圍線積分特征值提取及識別

局部圍線積分在進行特征向量提取時，經鑒別函數計算，求解出圍線積分雙譜中鑒別能力最強的前40圈，為了進一步減少測試模板庫存儲量和信息冗余以達到實時準確處理信息的目的，且更加直觀的看出鑒別能力最強的前40圈的圈數與能量熵、波形熵的關系，圖4、圖5畫出了鑒別能力最強的前40圈的圈數與能量熵、波形熵的變化曲線圖，其中S1、S2、S3分別代表三部雷達信號源信號的雙譜。

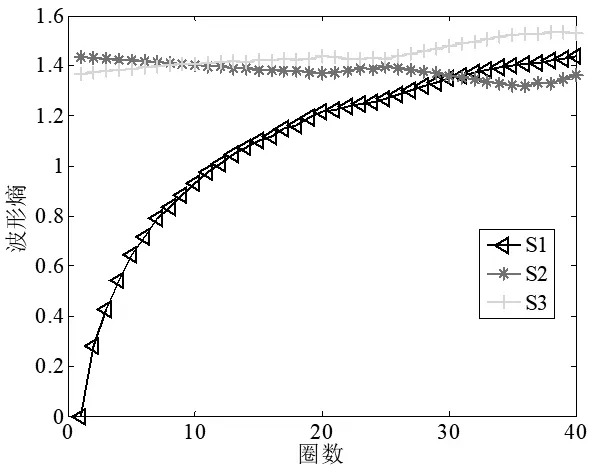
圖4 波形熵與積分圈數的關系圖

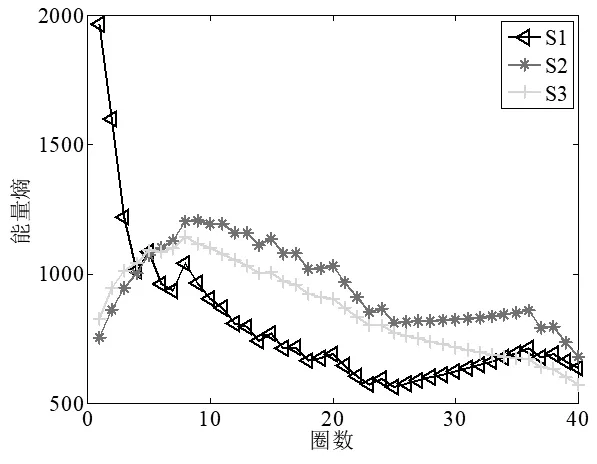
圖5 能量熵與積分圈數的關系圖

由圖4、圖5積分路徑圈數與能量熵、波形熵的變化曲線可知，在利用能量熵、波形熵作為特征向量識別時，三部雷達信號源信號的雙譜在局部圍線積分中前18圈積分路徑已具備了具有最優鑒別能力。因此，針對局部圍線積分雙譜中前18圈積分路徑的波形熵和能量熵，與計算出奇異值熵兩兩組成二維特征向量，利用已經設計好的分類器進行分類識別，仿真圖如圖6、圖7、圖8所示。

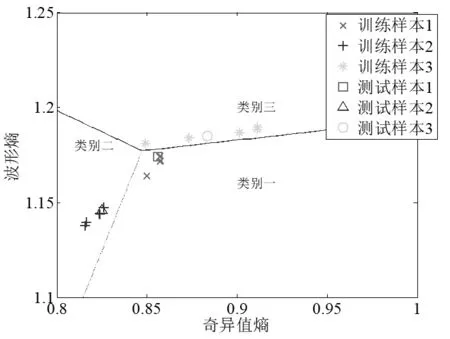
圖6 Es和Eb二維特征向量的識別

圖7 En和Es二維特征向量的識別

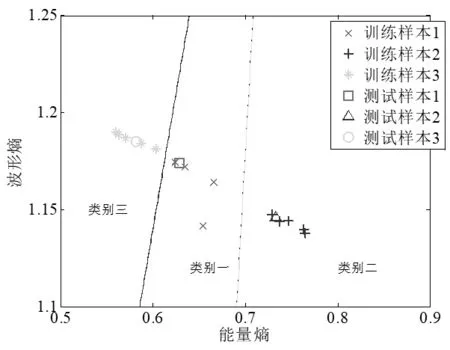
圖8 En和Eb二維特征向量的識別

表2為實載頻分別為20MHz、40MHz、80MHz、100MHz、200MHz時，局部圍線積分法進行分類識別率。

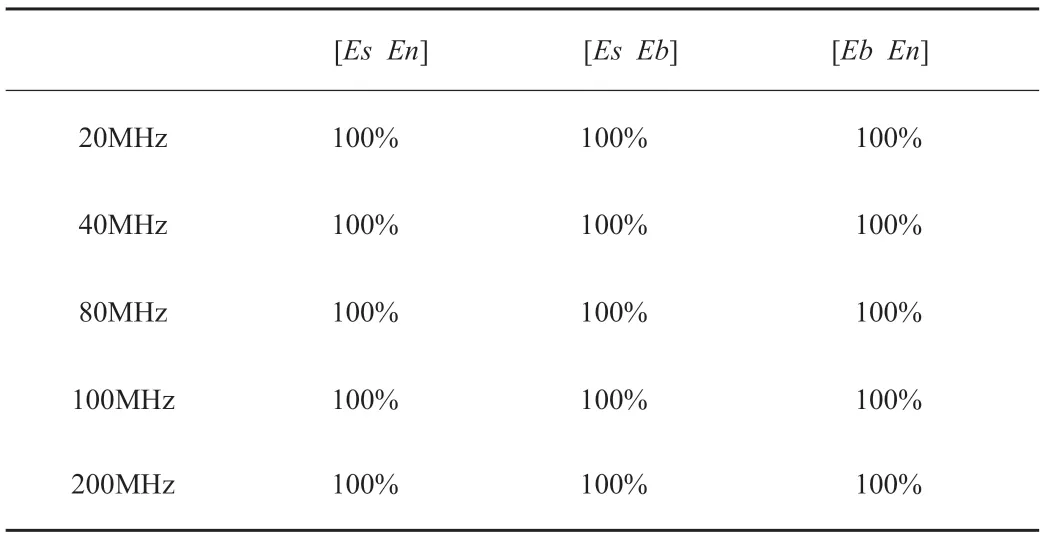
表2 局部圍線積分的分類識別率匯總表

由圖6、圖7、圖8和表2可知，局部圍線積分法識別率隨著載頻的增加沒有改變，提高了分類識別率。

本文根據圍線積分雙譜分析時存在目標模板庫巨大存儲量和信息冗余的缺陷，提出了局部圍線積分雙譜分析法，并進行二次特征值提取能量熵、波形熵和奇異值熵，構成雷達信號源分類識別的特征向量。通過實驗數據分析可知，與直接的圍線積分雙譜分析雷達信號源的識別率進行對比，驗證了局部圍線積分的二次特征值提取有效地提高了分類識別率。