機載陣列雷達風輪機回波信號建模與分析

何煒琨,劉 昂,王曉亮,張 瑩,陳 敏

(中國民航大學天津市智能信號與圖像處理重點實驗室,天津 300300)

0 引 言

過往研究發現,地基雷達在進行目標監視、氣象觀測等工作時會受到風力發電場的影響,運作性能受到嚴重干擾。而對于機載雷達來說,這類影響更為復雜且難以應對[1-3]。為了實現機載雷達風電場雜波抑制和目標檢測,研究機載雷達風輪機的電磁散射特性及回波仿真技術尤為重要。

目前,風輪機的電磁散射特性及其回波仿真技術主要是針對地基雷達[4-9],對機載雷達的研究較少。Naqvi[10]利用短時傅里葉變換(short time Fourier transform,STFT)分析了1∶160風輪機計算機輔助設計(computer aided design,CAD)模型散射回波的時頻特征,探究雷達處于機載高空平臺時,地面反射回波對風輪機散射特性的影響。Bhalla等人[11]利用風輪機CAD模型,發現風電場回波在距離-多普勒譜上會產生偽影,干擾目標信號,影響機載地面運動目標指示(ground moving target indication,GMTI)的性能。另外,Cai等人[12]在研究風電場對多功能機載監視雷達的影響時,認為風輪機葉片材料為理想導體,并利用物理光學(physics optical,PO)方法計算風輪機縮微模型[4,13]的散射回波,但沒有給出機載雷達陣列天線風輪機回波信號模型。

上述研究均通過建立風輪機的三維模型,然后再研究其電磁散射特性,但這種方式的風輪機模型制作方法較為困難,不方便修改參數,且操作復雜,計算量大且耗費時間。Mamgain[14]等人對機載監視雷達的風輪機回波進行了仿真,并結合真實數據,通過距離-多普勒譜對所構建的模型進行了驗證。但其只給出了單通道的回波模型，沒有給出機載陣列雷達各通道風輪機回波,且沒有對風輪機回波信號特性進行具體分析,無法全面了解風輪機的回波特征。

目前,陣列天線雷達在機載雷達中的應用越來越廣泛,其可以通過空時濾波有效地去除地面雜波,減緩雜波的干擾,在目標監視和氣象監測方面發揮著極其重要的作用。基于這種情況,本文將機載陣列天線回波模型與風輪機散射點疊加模型相結合,研究了當雷達處于機載平臺時,陣列天線風輪機的回波建模問題,給出任一觀測點處機載平臺各通道風輪機回波模型,并將實驗結果與理論分析結果進行對比,從時頻譜、距離-多普勒譜和空時譜多個維度分析了機載陣列雷達風輪機回波的微動特征,驗證所建模型的有效性。

1 機載陣列雷達風輪機回波模型

風輪機主要由葉片、桅桿和輪機艙組成。本文結合風輪機散射點疊加理論[15],將風輪機回波等效為一系列薄圓片回波合成[16],構建風輪機葉片的回波模型,并進行特征分析。

圖1描述了典型的機載監視雷達場景。其中,以載機所在位置作為原點建立坐標系,飛行方向為Y軸正方向,速度為V，線陣陣元的排列方向為X軸正方向,陣元間隔為d，風輪機相對于雷達的方位角θ為雷達視線(line of sight,LOS)在XOY面內的投影與Y軸的夾角,俯仰角φ為雷達LOS與XOY面的夾角,α和β分別為陣元夾角和速度夾角,波束直接照射風輪機葉片軸心。

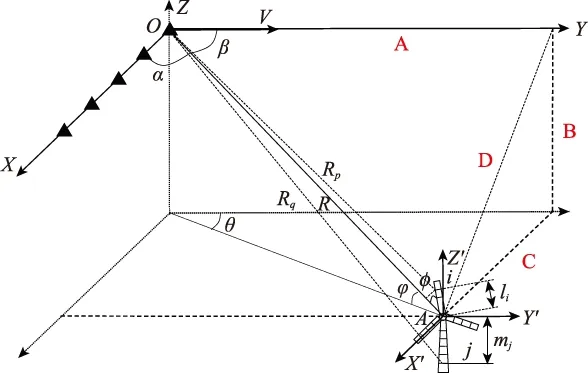
圖1 風輪機與機載雷達幾何關系圖Fig.1 Geometric relationship graph between wind turbine and airborne radar

假設雷達所發射的信號為線性調頻信號(linear frequency modulation,LFM),令up(t)表示單個LFM的復包絡,即

(1)

式中,A為信號幅度;T為脈沖寬度;μ=2πB/T,B為帶寬;rect(t/T)為矩形窗函數。

設雷達陣元發射相參脈沖串[17]為

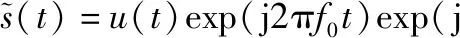
(2)

(3)

式中，Tr為脈沖重復周期;K為脈沖串中的脈沖數。

第n個陣元接收到的單個散射點i的回波信號[17]可表示為

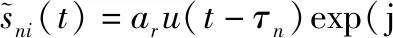
(4)

式中,ar表示散射點回波信號復幅度;τn為第n個陣元接收到的回波信號延時；θi和φi分別為散射點i的方位角和俯仰角;ft(θi,φi)為散射點i由于載機速度所產生的多普勒頻率:

(5)

式中，λ為波長。

(6)

則式(4)可進一步寫為

(7)

式中，τt=2Ri(t)/c,c為光速，Ri(t)為葉片上任一散射點i到達雷達的距離；li為散射點i到風輪機軸心的距離，由于(li/R)2→0[15],故

(8)

式中，φ(t)為葉片與雷達LOS的夾角;R為風輪機軸心與雷達的距離。因此,由于路徑引起的相位差[15]為

(9)

另外,第n個陣元相對于參考陣元的相位差[17]可表示為

(10)

定義該散射點的歸一化空間角頻率為

(11)

假設雷達發射信號滿足窄帶條件,則回波信號的復包絡在陣元間保持恒定[17],且由式(9)～式(11)可知,式(7)可進一步寫為

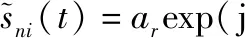
(12)

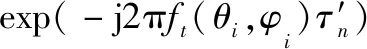
(13)

設一個葉片可以分為I個散射點,則整個葉片的回波信號為

exp[j2πft(θi,φi)t+j(n-1)ωs(θi,φi)]·

(14)

設風輪機有G個葉片(一般為3),葉片與雷達LOS相應的夾角為φg(t),于是所有葉片總的回波信號可寫為

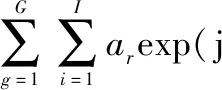
exp[j2πft(θi,φi)t+j(n-1)ωs(θi,φi)]·

(15)

式中,第g個葉片與雷達LOS的夾角余弦值cosφg(t)利用空間兩直線夾角公式[15]推導為

cosφg(t)=cosθcosφcosγg(t)+sinφsinγg(t)

(16)

式中，γg(t)為第g個葉片與水平軸Y′負方向的夾角,定義其為葉片夾角。

若j是桅桿上的任一點,其到葉片軸心的距離為mj;桅桿上任意一點j到雷達的距離為Rj[15],則

(17)

雷達第n個陣元接收到的散射點j的回波信號為

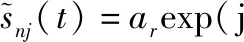
(18)

與葉片回波推導過程類似,求出整個桅桿的回波信號并進行下變頻,最終得出第n個陣元接收到的桅桿回波信號為

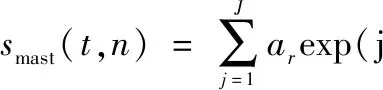
exp[j2πft(θj,φj)t+j(n-1)ωs(θj,φj)]·

(19)

式中,J為桅桿散射點數。因此，第n個陣元接收到的風輪機回波可表示為

sWT(t,n)=sblade(t,n)+smast(t,n)

(20)

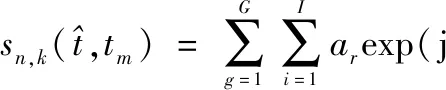
exp[j2πft(θi,φi)tm+j(n-1)ωs(θi,φi)]·

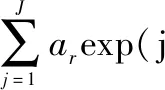
exp[j2πft(θj,φj)tm+j(n-1)ωs(θj,φj)]·

(21)

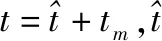
exp[j(k-1)ωt(θi,φi)+j(n-1)ωs(θi,φi)]+

exp[j(k-1)ωt(θj,φj)+j(n-1)ωs(θj,φj)]

(22)

另外,一般把某一特定距離單元內的風輪機回波對應空時二維數據寫入一個N行K列的矩陣:

(23)

式中,N為陣元數；K為脈沖數。通常為方便處理，把單距離單元的接收數據排成一個NK×1的列向量,即x=[x1,1,x2,1,…,xN,1,x1,2,x2,2,…,xN,2,…,x1,K,x2,K,…,xN,K]T。

2 機載陣列雷達風輪機回波信號時頻分析

由所建立的機載陣列雷達風輪機回波模型可知,其與地基雷達的風輪機回波模型[15]不同之處在于,由于載機具有速度,在雷達與風輪機徑向上的速度分量會產生額外的多普勒頻率。同時,由于不同時刻下的載機與風輪機的幾何關系不同,導致風輪機與雷達的姿態(如方位角,俯仰角等)發生變化,進而導致風輪機回波信號的微動特征更為復雜。

設載機的飛行高度為3 000 m,選取的風輪機參數參照金風82[20],葉片長度為40.25 m,桅桿高度為70 m,葉片旋轉速度設定為15 r/min,風輪機的旋轉面假定平行于圖1中所建立坐標系的YOZ平面。雷達發射信號為LFM,頻率為9.486 GHz,脈沖寬度為20 μs,脈沖帶寬為4.687 5 MHz,脈沖重復周期為100 μs,脈沖重復頻率(pulse repetition frequency,PRF)為10 kHz[12]。

本文采用STFT對風輪機的回波信號進行時頻分析[21],其定義為

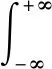
(24)

式中,g(t)為窗函數。

假設一個相干處理時間(coherent-processing interval,CPI)內脈沖數為64,載機速度為71 m/s,且在CPI內,雷達與風輪機的相對幾何關系不變。

設定風電場中風輪機的方位角θ=0°,軸心坐標為(0,10 000,-2 930)m,雷達位于坐標原點,LOS與風輪機的旋轉面平行,風輪機參考葉片夾角為γ=106°,得到風輪機回波信號時頻分析結果,如圖2所示。

圖2 風輪機回波時頻分析Fig.2 Time-frequency analysis of wind turbine echo

從圖2(a)可以看出,此時風輪機某葉片與雷達LOS垂直且遠離雷達,能量分布集中,地基雷達與機載雷達的回波時頻譜中出現多普勒閃爍,如圖2(b)所示。不同之處在于:一方面,對于機載雷達來說,由于載機本身具有速度,回波信號被調制,風輪機葉片回波產生的多普勒頻率在時頻譜上平移,同時由于葉片旋轉導致其對應的回波在平移的同時產生頻譜展寬。另一方面,機載雷達的回波中具有地雜波,同樣被載機速度調制,能量在整個時頻分析觀察時間內集中于載機速度所對應的多普勒頻率附近。另外,在0.003 8 s附近,葉片旋轉產生的多普勒閃爍與地雜波能量疊加,使得功率歸一化后其他位置的歸一化功率降低。

經推算可知,載機速度所產生的多普勒頻率ft為

(25)

單葉片葉尖回波所產生的最大多普勒頻率fWTmax為[15]

(26)

為便于分析不同照射條件下,風輪機葉片的時頻譜特性,下面對只有風輪機葉片的回波信號進行時頻譜分析。

2.1 葉片夾角對風輪機時頻譜的影響

設定風輪機的方位角θ=0°,軸心坐標為(0,10 000,-2 930)m,此時雷達LOS與風輪機的旋轉面平行,改變風輪機參考葉片與水平軸的夾角,得到不同葉片夾角的風輪機回波信號分析結果,如圖3所示。由圖2和圖3可以看出,與地基雷達類似的是,在俯仰角和方位角相同的情況下,雷達掃描到風輪機時,由于葉片夾角的不同,導致葉片回波信號的能量分布不同。當風輪機某葉片與雷達LOS垂直時,能量分布集中,時頻譜中出現多普勒閃爍。當風輪機3個葉片與雷達LOS均不垂直時,能量分布較為分散。但是由于載機本身具有速度,風輪機回波信號被調制,在時頻圖上表現為頻率搬移,且不同夾角下的搬移程度相同。由于仿真參數中的PRF相對較小,圖3時頻譜中都有頻率折疊的現象。

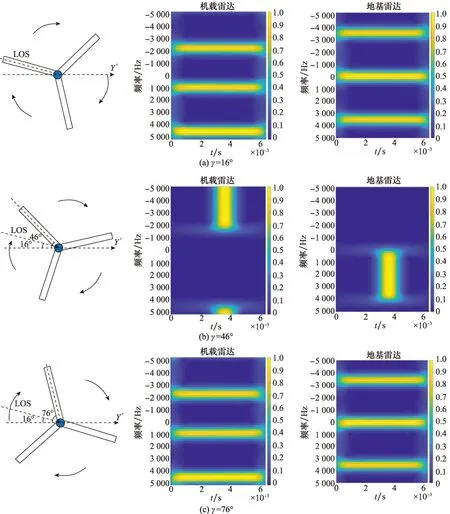
圖3 不同葉片夾角對時頻分析的影響Fig.3 Influence of different blade angles on time-frequency analysis

2.2 俯仰角和方位角對風輪機時頻譜的影響

在假定風輪機葉片與雷達LOS垂直的情況下,設定風輪機的方位角θ=0°,軸心坐標分別為(0,12 000,-2 930)m和(0,1 000,-2 930)m,得到不同俯仰角的風輪機回波信號分析結果,如圖4所示。

由式(5)可知,徑向的載機速度分量會根據俯仰角的改變而改變,所產生的多普勒頻率也會隨之變化。由圖4可看出,在方位角θ=0°的情況下,雷達掃描到風輪機時,等效葉片長度不變,垂直葉片轉動產生的多普勒閃爍寬度相同,而由于載機運動所引起的頻譜平移程度會受到俯仰角的影響:俯仰角越大,平移程度越小;俯仰角越小,平移程度越大。

在假定風輪機葉片與雷達LOS垂直的情況下,設定風輪機相對載機的俯仰角φ=30°,方位角θ分別為37°和53°,軸心坐標分別為(3 000,4 000,-2 930)m和(4 000,3 000,-2 930)m,得到不同方位角的風輪機回波信號分析結果,如圖5所示。

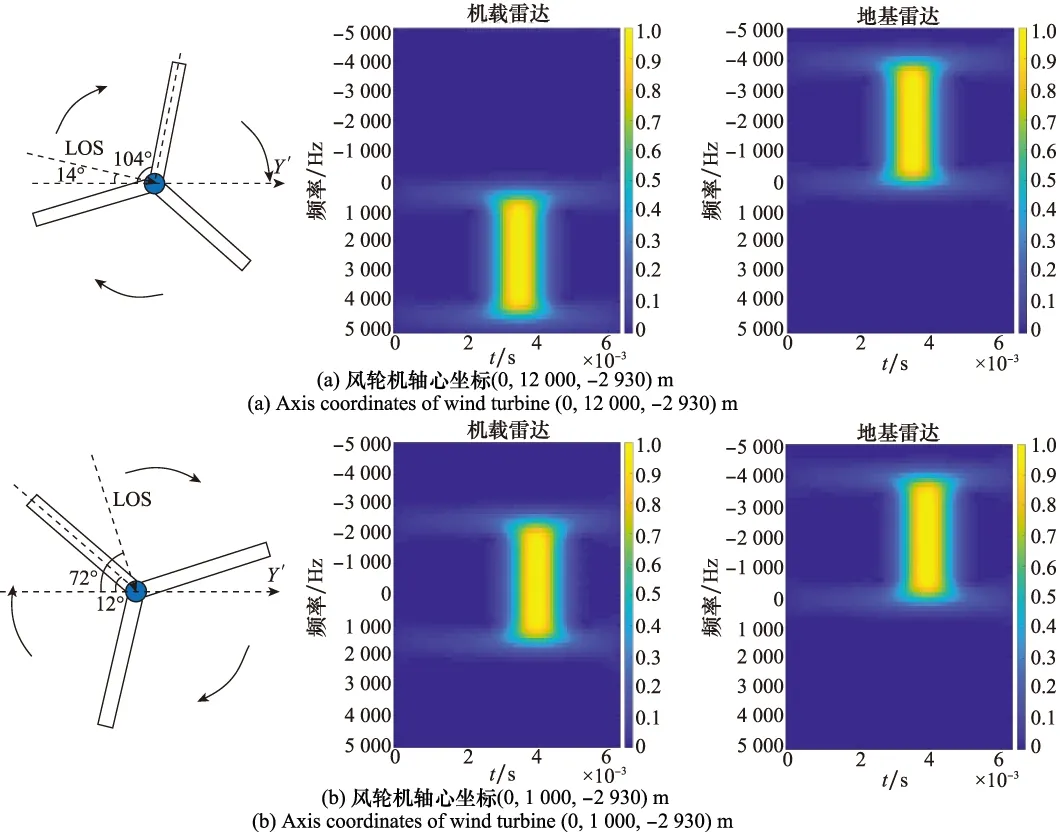
圖4 不同俯仰角對時頻分析的影響Fig.4 Influence of different pitch angles on time-frequency analysis

圖5 不同方位角對時頻分析的影響Fig.5 Influence of different azimuth angles on time-frequency analysis

同理,徑向的載機速度分量也會根據方位角的改變而改變,由圖5可看出,在俯仰角φ=30°的情況下,不同方位角風輪機所對應的時頻譜多普勒閃爍寬度不同,即葉片旋轉產生的最大多普勒頻率不同,且由于載機運動所引起的頻譜平移程度也會受到方位角的影響:方位角越小,閃爍寬度越寬,平移程度越大;方位角越大,閃爍寬度越窄,平移程度越小。

3 機載陣列雷達風輪機回波信號距離-多普勒分析

對軸心坐標為(0,10 000,-2 930) m的風輪機進行距離-多普勒分析如圖6所示。經計算得出,風輪機與機載雷達之間的距離為10 420 m,與實驗結果相符。從圖6中可以看出,當風輪機旋轉狀態處于圖2(a),即葉片夾角γ=106°時,風輪機回波在頻域上連續展寬,反射率較強,能量較大。另外,與第1節的時頻分析結果相同,由于載機本身的速度,風輪機回波信號被調制,譜圖上的展寬在縱軸頻域上整體平移。由式(25)和式(26)可以得出,此風輪機回波所對應的ft和fWTmax分別為4 309 Hz和3 998 Hz,與距離-多普勒譜中的表現形式相符。

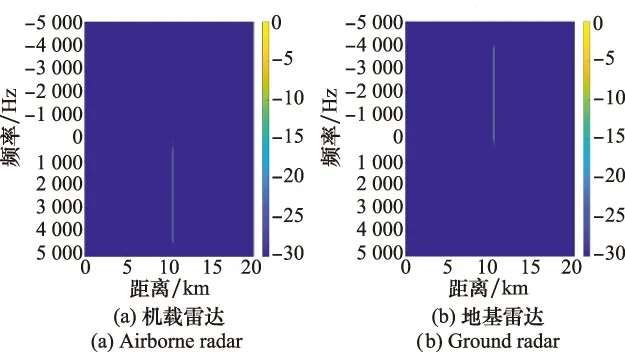
圖6 風輪機回波距離-多普勒分析Fig.6 Range-Doppler analysis of wind turbine echo

同理可以證明,不同葉片夾角、俯仰角和方位角,對機載陣列雷達風輪機回波信號的距離-多普勒特征的影響規律與時頻譜的影響規律相同:在載機飛行方向與風輪機旋轉面平行的情況下,俯仰角和方位角越大,平移程度越小;俯仰角和方位角越小,平移程度越大。另外,方位角也會影響垂直葉片產生的頻譜展寬,方位角越小,展寬越大;方位角越大,展寬越小。

4 機載陣列雷達風輪機回波信號空時譜分析

為了研究機載陣列雷達下風輪機回波的空時域特征,設陣元數為32個,風輪機與雷達的其他參數不變,風輪機的旋轉面假定平行于XOY面。

對風輪機進行空時二維譜分析,設定風輪機軸心的位置為(0,10 000,-2 930)m,此時雷達LOS與風輪機的旋轉面平行,風輪機參考葉片與水平軸的葉片夾角為106°(見圖2(a)),歸一化處理結果如圖7所示。

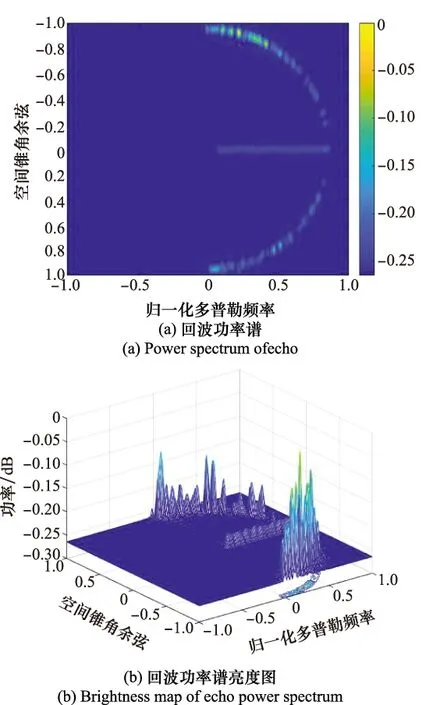
圖7 回波空時譜(γ=106°)Fig.7 Space-time spectrum of echo (γ=106°)

仿真實驗中,風輪機雜波對應的雜噪比為32 dB,地雜波對應的雜噪比為40 dB。由圖7可以看出,地雜波在空時譜中表現為橢圓形的分布(天線陣列軸線與載機航向垂直,由空域錐角與多普勒頻率之間的關系可知,此時雜波分布為正橢圓),而當風輪機的某一葉片與雷達LOS垂直時,風輪機回波在多普勒域存在明顯展寬,總體表現為一條“窄帶”。

由風輪機的位置和式(10)可知,其空間角余弦cosα=0,與圖7(a)中“窄帶”在空域的位置相符。另外由式(25)和式(26)可知,該風輪機回波所對應的ft=4 309 Hz,葉片轉動產生的fWTmax=3 998 Hz,且由于此刻垂直葉片遠離雷達旋轉,所以該情況下的風輪機回波的最小多普勒頻率和最大多普勒頻率應為fdmin=ft-fWTmax=311 Hz和fdmax=ft=4 309 Hz。根據歸一化多普勒頻率2fd/PRF可知,風輪機回波所對應的最小歸一化多普勒頻率和最大歸一化多普勒頻率應為0.062 2和0.861 8,與空時二維譜中“窄帶”在多普勒域的擴展情況相符,理論分析與實驗結果一致。

對于機載前向陣來說,地雜波在空時譜上的分布是固定的,但風輪機雜波會在不同的參數下與前向陣的雜波帶呈現不同的分布。設定風輪機參考葉片夾角為46°,結果如圖8所示。

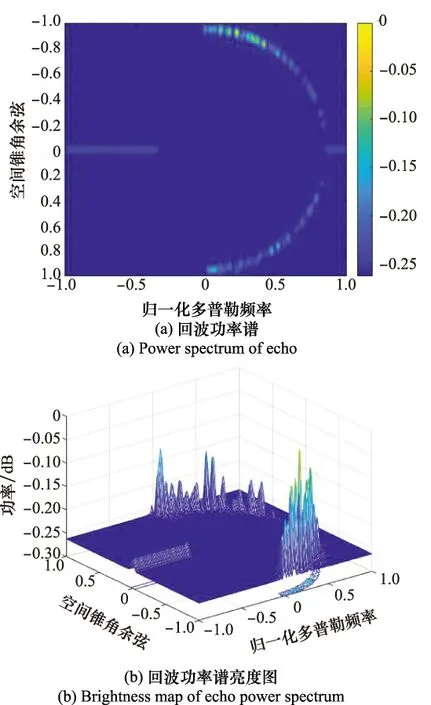
圖8 回波空時譜(γ=46°)Fig.8 Space-time spectrum of echo (γ=46°)

由圖8可以看出,當葉片夾角為46°時,此刻與雷達LOS垂直的風輪機葉片朝向雷達旋轉,產生正向的多普勒頻率。風輪機“窄帶”由歸一化多普勒頻率0.861 8處向正向擴展,擴展寬度與葉片夾角為106°時相同。另外,由于PRF的限制,造成多普勒頻率折疊。由此可見,對于不同參數下的風輪機葉片,其回波在空時譜中的表現形式不同。

為便于分析不同照射條件下,風輪機葉片的空時譜特性,下面對只有風輪機葉片的回波信號進行空時譜分析。

4.1 葉片夾角對空時二維譜的影響

設定風輪機的方位角θ=0°,軸心坐標為(0,10 000,-2 930)m,此時雷達LOS與風輪機的旋轉面平行,改變風輪機參考葉片與水平軸的夾角,與圖3一致,得到不同葉片夾角的風輪機回波信號空時譜,如圖9所示。

由圖9可以看出,隨著風輪機葉片夾角的不同,風輪機回波在空時二維譜中所表現的形式也隨之不同:當雷達LOS與風輪機某一葉片垂直時(見圖7(a)和圖9(b)),風輪機回波在多普勒域存在明顯展寬,表現為一條“窄帶”,且葉片遠離雷達和朝向雷達時的“窄帶”關于載機速度所對應的歸一化多普勒頻率點對稱;當雷達LOS與風輪機各葉片不垂直時(見圖9(a)和圖9(c)),由于散射點回波能量相消,在空時二維譜中沿多普勒域能量發散,能量主要集中在葉尖所產生多普勒頻率上,同時由于PRF的限制,圖9空時譜具有多普勒頻率折疊的現象。

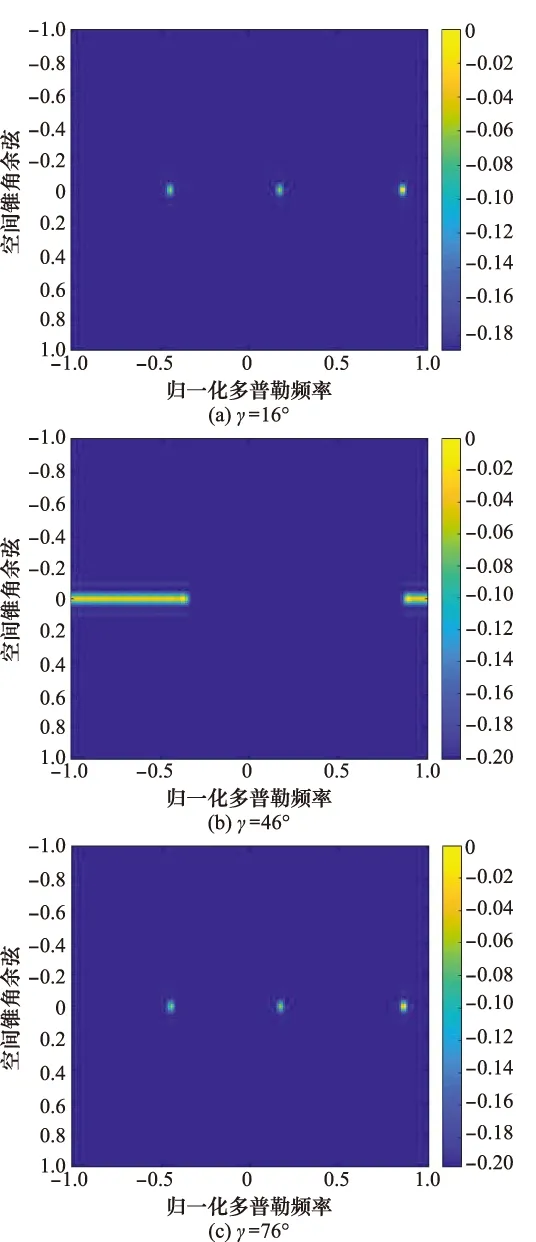
圖9 不同葉片夾角對空時二維譜的影響Fig.9 Influence of different blade angles on space-time two-dimensional spectrum

4.2 俯仰角和方位角對空時二維譜的影響

在假定風輪機葉片與雷達LOS垂直的情況下,設定風輪機的方位角θ=0°,軸心坐標分別為(0,12 000,-2 930)m和(0,1 000,-2 930)m,此時雷達LOS與風輪機的旋轉面平行,得到不同俯仰角風輪機回波信號的空時譜,如圖10所示。

在假定風輪機葉片與雷達LOS垂直的情況下,設定風輪機相對載機的俯仰角φ=30°,方位角分別為37°和53°,軸心坐標分別為(3 000,4 000,-2 930)m和(4 000,3 000,-2 930)m,得到不同方位角風輪機回波信號的空時譜,如圖11所示。

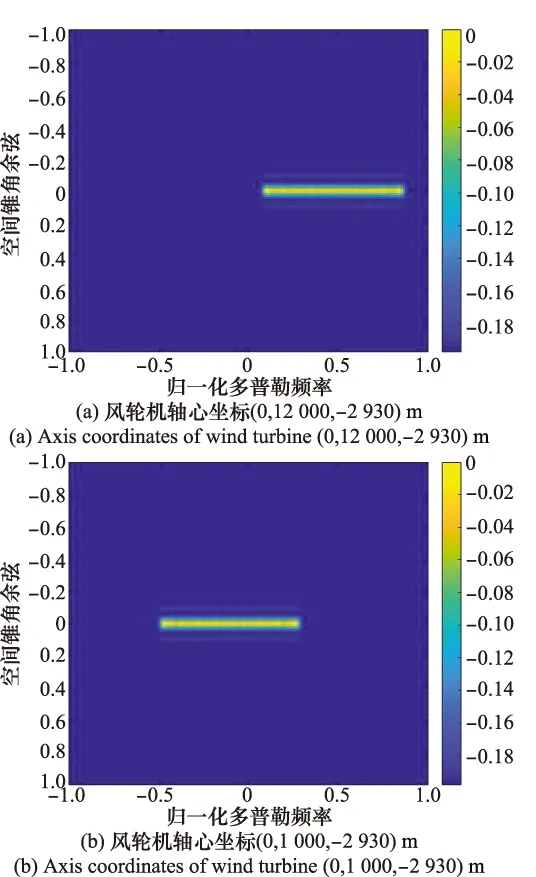
圖10 不同俯仰角對空時二維譜的影響Fig.10 Influence of different pitch angles on space-time two-dimensional spectrum

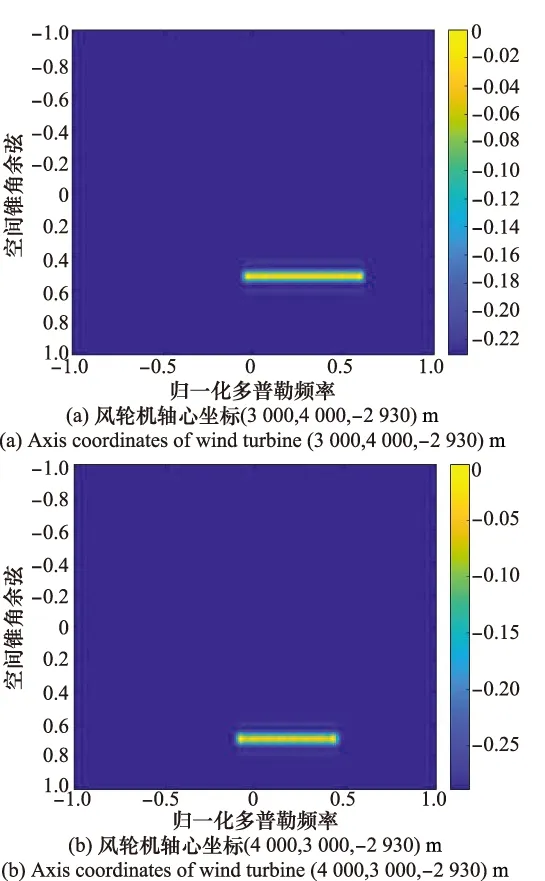
圖11 不同方位角對空時二維譜的影響Fig.11 Influence of different azimuth angles on space-time two-dimensional spectrum

由式(10)可知,當方位角θ=0°時,圖10(a)和圖10(b)中風輪機回波的能量都集中在cosα=0附近,而兩者葉片轉動產生的最大多普勒頻率相同,所對應的“窄帶”寬度相同。不同之處在于由于俯仰角不一樣,載機速度在風輪機徑向方向上的分量不一樣,影響“窄帶”在多普勒域的位置。當俯仰角φ=30°時,風輪機的空間錐角余弦值隨著方位角變化而變化,方位角越大,cosα值越大,如圖11所示。另外,由于兩位置風輪機的等效葉片長度不同,轉動產生的最大多普勒頻率不同,所對應的“窄帶”寬度有所差異,方位角越大,“窄帶”寬度越小。

5 結 論

本文以風輪機為研究對象,建立了對于機載陣列雷達任一觀測點處的風輪機回波信號模型,從時頻域、距離-多普勒域和空時域對該情況下的風輪機回波信號微動特征進行分析,結果如下。

(1) 風輪機回波信號在機載平臺下的表現形式與地基雷達不同,主要區別在于,地基雷達與風輪機的位置都是固定的,風輪機的位置參數不變。而對于機載雷達來說,由于雷達平臺的運動,風輪機相對載機的方位角和俯仰角信息會不斷改變,其微多普勒特征也會隨之變化。

(2) 雷達平臺自身的速度會使風輪機的回波信號得到調制,使得風輪機葉片轉動產生的多普勒頻率在時頻譜、距離-多普勒譜和空時譜的多普勒域整體平移,而俯仰角和方位角會影響平移的程度,在0°～90°的范圍內,俯仰角和方位角越大,平移程度越小;俯仰角和方位角越小,平移程度越大。

(3) 除平臺速度會對回波信號調制,影響其在時頻譜中的表現形式外,風輪機相對平臺的位置和葉片夾角也會影響風輪機回波信號的時頻特征。當平臺的運動方向與風輪機的旋轉面平行時,風輪機葉片與雷達LOS非垂直情況下的回波信號在時頻譜中的能量分布比較分散,而當風輪機葉片夾角改變使得葉片與雷達LOS垂直時,能量分布集中,時頻譜中出現多普勒閃爍,方位角會影響閃爍的寬度:方位角越小,閃爍寬度越寬;方位角越大,閃爍寬度越窄。

(4) 當平臺的運動方向與風輪機的旋轉面平行時,不同葉片夾角的風輪機回波在空時二維譜中的表現形式不同。葉片與雷達LOS垂直時,其頻譜特征表現為一條“窄帶”;葉片與雷達LOS不垂直時,其頻譜能量較為發散,主要由各葉片的葉尖產生。俯仰角固定的情況下,風輪機相對雷達的方位角會影響回波最大多普勒頻率及空域角頻率,在0°～90°的范圍內,方位角越大,空間錐角余弦值越大,最大多普勒頻率越小;方位角越小,空間錐角余弦值越小,最大多普勒頻率越大。