面向多類別分類問題的子抽樣主動學習方法

施 偉,黃紅藍,馮旸赫,劉 忠

(國防科技大學系統工程學院,湖南 長沙 410073)

0 引 言

有監督學習是利用標記樣本不斷調整模型參數以達到性能要求的過程。隨著技術進步,能夠獲取大規模樣本數據,提高模型預測性能。然而,即使是對相關領域內的專家來說,給數據加上標簽也常常是一項昂貴和耗時的任務。文獻[1]中使用的數據集收錄了總計367 835字的實驗樣本，用于軍事文本的命名實體識別實驗。在文獻[2]所研究的航天遙感圖像場景分類問題中，一個普通規模的數據集包含31 500張涉及45類場景類別的圖像樣本，每個樣本至少包含196 608個像素。豐富的圖像變化、類內多樣性和類間相似性使得標注這類數據集更具挑戰性。

為解決這類問題,主動學習方法應運而生,用于對未標注數據集的自動標注。文獻[3-4]中的策略傾向選擇具有最大不確定性的樣例交給專家進行標注,使用盡量少的樣例獲得盡可能高的分類性能。文獻[5-6]中的基于專家委員會投票的查詢策略是訓練一個分類器委員會,并選擇最具分歧的實例來分析查詢,是一種從隨機輸入流中過濾信息的方法。上述主動學習策略都屬于短視主動學習的范疇,共同的缺點是只根據已標注實例的信息和基于此訓練出的分類器來選擇將要查詢的實例,忽略了大量未標注實例的分布信息。

鑒于上述算法的缺陷,另一類算法試圖從大量未標記實例中獲取信息,建立一個對問題域中不可見的實例具有良好泛化性能的分類器。比如文獻[7]中總結了一種減小數據集樣本標注前后泛化誤差的方法。與之相似的方法是通過減少模型方差來間接最小化泛化誤差,比如文獻[8-9]。文獻[10]利用未標注樣本的先驗概率p(x)作為不確定度的權值。文獻[11]使用了相似的框架,使用余弦度來測量信息密度。

與查詢單個實例的方法不同,批量模式的主動學習方法會選擇一批樣本進行查詢。當批處理規模較小時,又衍生出一類小樣本主動學習方法[12-13],該方法認為批量設置越小,選擇標準更新越快,越能促進學習性能的提升。

也有一類不需要真實標簽對樣本進行標注的主動學習方法[14-15],這類方法試圖最小化統計模型的期望方差,并在計算這類方差時省略標簽信息。但是,因為這種方法沒有真正利用樣本的標簽信息,只關注具有代表性的實例,因此即使標注的實例具有有效信息,仍不被算法利用。文獻[16]通過引入多個偽標注器,一定程度上改善了這類小樣本主動學習方法的性能,但本質上仍存在上述缺點。

然而當前主流的主動學習方法[5,17-19]都需要很強的計算能力,導致主動學習很難應用于數據量過大的現實問題。因此,迫切需要一種有效的方法解決這類問題。有一些研究試圖將聚類算法與主動學習相結合的嘗試。比如，文獻[20]將分類和聚類結合,避免同一聚類中的樣本被重復標記,但該方法局限于線性邏輯回歸,僅證明了聚類信息的優越性。文獻[21]提出譜聚類和K均值聚類組合的方法,通過提取有代表性的特征向量,輔助支持向量機進行分類,但計算量很大,并未考慮算法效率。文獻[22]提出模糊核聚類的方法,但該方法只是為了篩選出日志數據的冗余樣本。文獻[23]直接將最具代表性的聚類樣本分類結果作為聚類的標簽。文獻[24]引入隨機森林概念,重點在于對聚類算法的創新。

本文提出一種基于子抽樣的主動學習(subsampling-based active learning,SBAL)算法,整合了無監督聚類算法和傳統主動學習方法。首先,采用無監督聚類算法對數據集進行粗略的聚類。然后,提取聚類結果的部分子類別,即所謂的子抽樣,減少單次計算的樣本數據規模。最后,應用主動學習方法,對子抽樣進行分類標注。經過多次迭代,實現對原始數據集的全部分類標注。所提算法在Binary Alphadigits和OMNIGLOT兩個標準數據集上進行了實驗,實驗結果證明,所提算法能打破傳統主動學習方法不能處理大規模數據集分類標注問題的局限性。算法的創新點在于除了將無監督聚類與主動學習算法相融合,還在二者之間增加了子抽樣操作,該操作能夠顯著降低算法的時間復雜度,在保證實驗準確率的基礎上減少實驗耗時,從而更加高效地處理大規模數據集的分類問題。

1 SBAL模型框架

1.1 無監督聚類

為解決主動學習無法處理大規模數據標注的問題,在進行主動學習前,引入一個無監督聚類的環節。本文框架使用的是K均值聚類算法[25-27],主要包含以下4個步驟。

步驟 1K值的選擇:隨機選取K個樣本作為初始的聚類中心,聚類中心的數量由用戶給出,記為K。實際問題中,往往已知樣本類別總數,因此在進行聚類處理時,將K值設定為樣本類別總數。

步驟 2距離度量:在將對象點分類到距離聚類中心最近的簇中時,需要用到最近鄰的度量策略。在歐氏空間中采用的是歐式距離,在處理文檔對象時,采用余弦相似度函數,有時候也采用曼哈頓距離為度量,需要根據不同情況進行選擇。設第i個樣本為xi,第j個聚類的質心為Centerj,數據點xi到質心Centerj的距離為dist(xi,Centerj),以下是不同類型的距離公式。

歐氏距離:

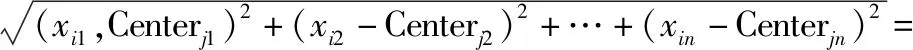
(1)

余弦相似度:

(2)

式中,A與B分別表示xi和Centerj向量。其中,分子為A與B的點乘,分母為二者各自的L2范數相乘。

曼哈頓距離:

(3)

用以標明兩個點在標準坐標系上的絕對軸距總和。

步驟 3新質心的計算:經過步驟2,得到K個新的類,每個樣本都被分到K個類中之一。之后,樣本的質心就會失效,需要計算每個類的新質心。對于分類后產生的K個類,所有樣本點的坐標均值即為新質心。假設第j個類包含的數據點有xj1，xj2，…，xjm,則新質心的坐標為

(4)

步驟 4判斷算法是否停止:當兩次迭代差值ΔJ小于迭代終止閾值δ,或是達到設定的最大迭代次數itermax時,算法停止。否則,循環執行步驟2～步驟4。

K均值算法雖然有效,但是容易受到初始質心設置的影響。一般情況下,在對樣本數據分布狀況不可知的情況下,初始質心的設定是隨機的,所以算法容易陷入局部最優。通常會進行大量重復實驗,尋找效果最優的初始設定。

1.2 子抽樣

經過對原始數據集的無監督聚類后,得到聚類結果

L={L1,L2,…,LK}

(5)

式中,L是全部子類的集合;Lh表示第h個聚類,h∈[1,K]且h∈Z。

根據需要,隨機在集合L中選擇p個元素,組成新的集合。子集設為

Lsub,p={Ls1,Ls2,…,Lsp}

(6)

式中,p表示選取的子類個數,p∈[1,K]且p∈Z。

將Lsub,p作為新的未標記數據集,供主動學習算法使用。因為主動學習的性能受數據集影響較大,所以p值需要根據實際情況進行選擇,合適的p值會帶來性能的提升。

1.3 主動學習方法

原理上,所有主動學習方法均可以應用本算法流程,但本框架只采用以下5種當前主流的主動學習算法進行設計。

(1) 隨機抽樣

在抽取的每個子集上均勻隨機抽取指定數量的樣本作為訓練數據,隨機抽樣的方法常作為所有主動學習方法的基準線。

(2) 不確定性采樣[17,28]

采用基于信息熵的不確定性采樣作為查詢樣本的標準:

(7)

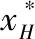
(3) 基于專家委員會投票的查詢[5,29]

該方法旨在尋找與當前子集上標記訓練數據一致的最小化的版本空間。本文采用“袋裝”查詢的方法,“袋裝”是從輸入樣本中重新采樣,得到一個固定的分布,通過對得到的假設的輸出進行平均，得到最終的假設。該方法基于預測誤差，由“偏差”和“方差”兩部分組成,“偏差”是輸入數據大小所必需的估計誤差,“方差”是具體數據存在的統計差異。“袋裝”可以隔離這兩個因素,并且可以最小化誤差的方差。假設每個子集上一共進行T次查詢,因此,在第t時刻查詢的樣本為

(8)

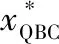
(9)

(4) 密度加權[18,30]

采用子抽樣的方法對基于圖的密度加權方法進行改進。基于圖的密度加權方法通過構建k近鄰的圖結構來描述樣本間的關系,并用鄰接矩陣來表示。每個子集上構建的圖結構是對稱的,其中兩個樣本之間的權重表示為

(10)

式中,Wi j表示鄰接矩陣;Pi j表示第i個樣本屬于第j類的概率值;σ表示整體樣本分布方差。為了區分具有多個權重較小的領域的數據點,通過邊的數量對這些權值進行歸一化處理,查詢樣本的計算公式為

(11)

(5) 基于學習的主動學習[19]

對于每一個子集,模型訓練一個回歸器,通過將查詢選擇過程表述為回歸問題,預測每個子集上的候選樣本的期望誤差縮減。在每個子集上,通過選擇樣本進行標簽查詢:

(12)

式中,t表示當前迭代查詢次數;Ut表示當前子集上未標記的數據集合;g(·)表示一個回歸函數,可以預測在給定分類器狀態下注釋特定樣本的潛在誤差縮減;Φt表示當前子集上參數化的分類器;Ψx表示當前子集上未標記樣本的特征參數。

1.4 標準框架

SBAL算法標準框架的流程圖如圖1所示。SBAL算法集成了多個子方法,是對主動學習算法解決分類問題的改進,其主要思想如下:因為性能優秀的主動學習算法,都有著極大的計算量,很大程度上限制了實驗數據集的規模。當遇到大數據集的實際問題時,就很難直接使用現有主動學習算法訓練分類器。為解決這一問題,第一步，對原始數據集無監督聚類,雖然其分類效果不如主動學習算法,但是可以初步實現數據集的大致分類。第二步,隨機選取一部分子類作為原始數據集的子抽樣,通過對聚類結果子抽樣,縮小單次計算的樣本數規模,進而簡化主動學習方法的處理難度。第三步,將子抽樣數據集作為未標注數據集,由主動學習算法進行訓練,完成標注。重復執行第二步和第三步,實現全部樣本的標注。

1.5 算法復雜度分析

算法的時間復雜度很大程度上反映了算法的效率,是衡量算法優劣的一個重要指標。本節旨在分析時間復雜度,證明采用本文算法相較于傳統采樣算法,性能有所提升。

為便于分析,假設整個樣本集的數據規模為n,當n足夠大時,樣本大致均勻分布于m類,每類包含m/n個樣本。使用SBAL算法時,子抽樣集所包含的種類數為M,樣本規模為nM/m。因為相較于主動學習算法,K均值聚類算法的時間復雜度O(n)較低,且實現簡便,可在實驗預處理階段獲得,因此可以忽略。本節只需對主動學習階段采樣策略的算法復雜度進行分析。

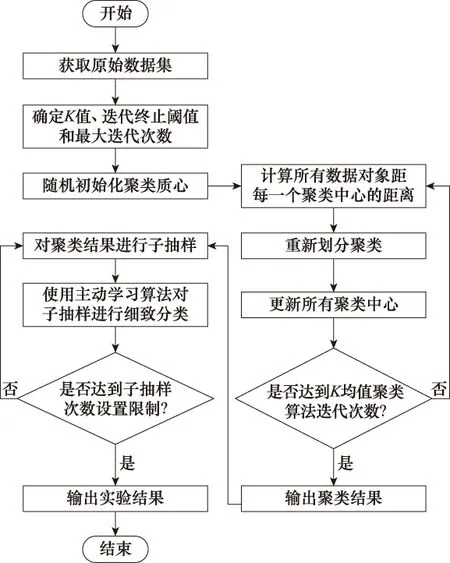
圖1 SBAL算法標準框架流程圖Fig.1 Flow chart of SBAL algorithm standard framework

1.5.1 基于隨機抽樣的查詢策略

傳統隨機采樣直接在全部未標注樣本集中隨機選取采樣點,時間復雜度為O(n)。當采用SBAL算法后,每個子集的數據規模為nM/m,子集數目為m/M,因此時間復雜度為O(n)。雖然時間復雜度相同,但隨機抽樣策略的實驗性能較差,很少應用。因此比較復雜度的意義不大。

1.5.2 基于不確定性采樣的查詢策略

采用SBAL算法后,單個子抽樣集計算的時間復雜度僅為O(M3n/m),經過重復抽樣后,復雜度增加為O(M2n)。可以看出當數據集規模十分巨大,類別數目m較多時,采用小規模子抽樣,可得到M2?m2,使時間復雜度較大程度的降低。

1.5.3 基于專家委員會投票的查詢策略

假設專家委員會成員數為c。該算法需要首先計算所有委員會成員類條件概率,時間頻度為T(n,m,c)=((m+1)c+3)m,再計算兩個條件概率分布的信息度量,時間頻度為T(n,m,c)=(((m+1)c+3)m)c,遍歷所有樣本后為T(n,m,c)=(((m+1)c+3)m)cn,經整理,時間復雜度為O(m2c2n)。

當采用SBAL算法時,單個子抽樣集計算的時間復雜度僅為O(M3c2n/m),經過重復抽樣后,復雜度增加為O(M2c2n)。同理,根據樣本規模較大的特點,有M2?m2,算法時間復雜度減少。

1.5.4 基于密度加權的查詢策略

使用密度加權的查詢策略,既要計算樣本的信息量,又要計算樣本在樣本空間中的密度信息,用于對信息量加權。信息量的計算與基于不確定性的查詢策略無異,時間頻度為T(n,m)=m(m+3),密度信息的計算時間頻度為T(n,m)=n,遍歷全部樣本點的總時間頻度為T(n,m)=m(m+3)nn,則時間復雜度為O(m2n2)。

采用SBAL算法,單個子抽樣集計算時間頻度為T(n,m)=(nM/m)2(M+3)M,復雜度為O(M4n2/m2),經過重復抽樣后,時間復雜度變為O((M3/m)n2),顯然在M?m時,可得M3/m?m2,使用SBAL算法相較于原算法復雜度也有所降低。

1.5.5 基于學習的查詢策略

本方法不同于傳統查詢策略的是,通過訓練回歸器在訓練中選擇能夠減少泛化誤差的未標記樣本進行查詢,然而不同的問題,樣本的特征參數Ψx會隨之變化,分類器的回歸函數g(·)也有所不同。

該策略雖然沒有固定公式用于定量分析時間復雜度,但可以定性分析。該策略通過使用簡單的特征(如分類器輸出的方差或特定數據點可能的預測標簽概率分布)訓練分類器的回歸函數。這一計算過程需要計算每個未標注樣本作為候選查詢樣本的期望誤差縮減,時間復雜度至少為O(n),此時,采用SBAL算法的時間復雜度也為O(n)。如果在計算期望誤差縮減時,選取更為復雜的函數,一旦原始策略時間復雜度成指數增加,那么采用SBAL算法的優勢將會明顯,M?m的條件會使算法時間復雜度大幅度減少。

2 實驗設計

將模型中5種基于子抽樣的經典主動學習方法應用到多類別數據標注的問題上,對基于子抽樣的經典主動學習在多類別數據上的性能進行實驗研究。

2.1 數據集

2.1.1 Binary Alphadigits

Binary Alphadigits數據集[31]是一個手寫字符圖像數據集,數據集中共有36類手寫字符,分別由26個大寫英文字母“A”至“Z”和10個數字字符“0”至“9”組成。數據集中每類字符由39個二值圖片組成,將每個樣本圖像補0擴大為20像素×20像素,因此每張圖片可以用一個400維的向量表示。數據集圖片如圖2所示。

圖2 Binary Alphadigits數據集圖片Fig.2 Image of Binary Alphadigits dataset

2.1.2 OMNIGLOT數據集

OMNIGLOT數據集[32]也是一個手寫字符圖像數據集。數據集是由50種不同字母組成的1 623類不同的手寫字符。每一類字符都是由不同的20個人通過亞馬遜公司的Mechanical Turk在線繪制的,一共32 460個樣本。每個圖像大小為105像素×105像素,在實驗中,將每個樣本圖像壓縮為28像素×28像素,因此每張圖片可以用一個784維的向量來表示。與Binary Alphadigits數據集相比,OMNIGLOT數據集更加復雜,因為數據集中的類別數量巨大,同時每類僅有少量樣本。因此,OMNIGLOT數據集成為了小樣本學習的標準數據集。數據集中的部分圖片如圖3所示。

圖3 OMNIGLOT 數據集圖片Fig.3 Image of OMNIGLOT dataset

2.2 參數設置

在實驗中,對每種主動學習算法,都采用子抽樣的方法,令其從數據集中選擇p類樣本組成實驗子集Lsub,p,其中p={3,5,8}。這里子集中的樣本很可能是不平衡的,可能一類存在很多樣本,而另一類可能樣本數很少甚至沒有。這種設置增加了實驗難度。由于主動學習算法需要標記樣本作為初始樣本,所以在每一個子集中都給定p個已標記樣本作為初始樣本,這些初始樣本分別來自不同的類別。對于無監督聚類后的數據集,抽取10 000個子集,即進行10 000次隨機實驗。其中,在每個子集上,按照80%為訓練集,剩余20%為測試集的方式劃分數據集。

2.3 實驗結果

2.3.1 Binary Alphadigits實驗結果

迭代結果如圖4所示。其中,橫軸為查詢次數(將初始給定標記樣本的數目作為橫軸的初始值),縱軸為性能指標準確率。在每一組實驗中都將最大查詢次數設置為總樣本數的80%,即最終使整個訓練集都被查詢。從圖4中可以看出,在Binary Alphadigits數據集上,隨著查詢次數的增多,各個算法的準確率都在上升,不同算法的準確率有所不同。由于每個回合(每個子集)上,給定每個算法的初始標記樣本數相同,因此各個算法初始時在測試集上的分類準確率相同。同樣,在回合結束時,由于最大查詢數目等于整個測試集的樣本數,所以對于不同算法,最終都將查詢完整個測試集后算法才停止該回合,因此所有算法最終的準確率也一致。

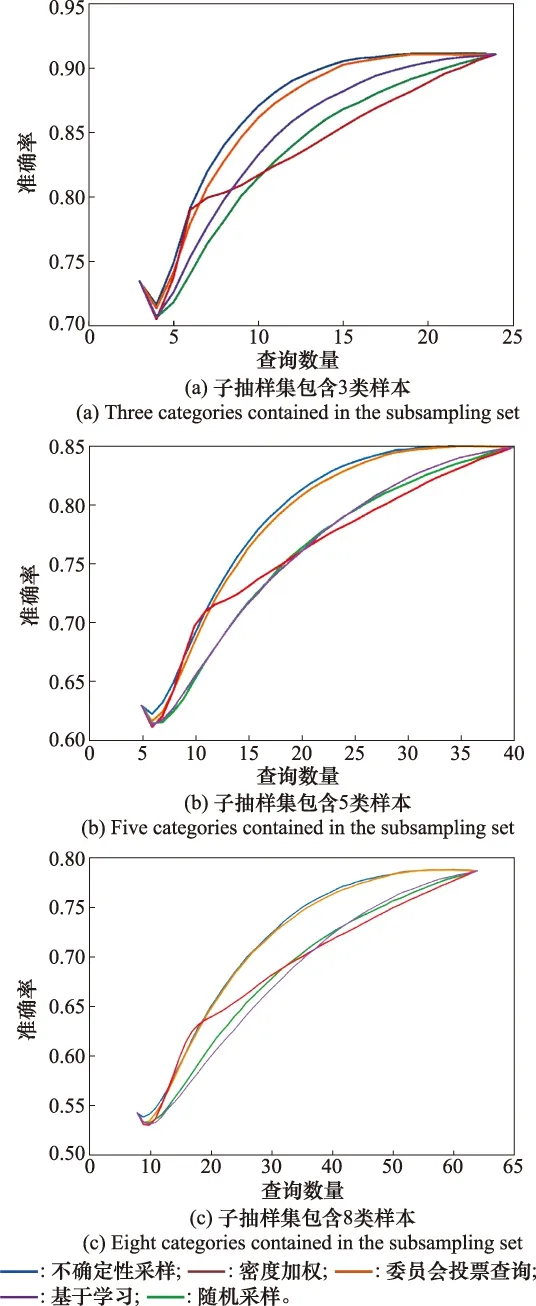
圖4 Binary Alphadigits數據集的算法性能對比Fig.4 Algorithm performance comparison of Binary Alphadigits dataset

各個算法的平均準確率如表1所示。根據表1中的結果,在Binary Alphadigits數據集上,基于不確定性采樣的主動學習模型的平均性能最好,達到的平均準確率最高。結合圖4可知,基于密度加權的主動學習算法在查詢樣本數較少的情況下能夠達到較高的準確率,但是隨著查詢數的增多,分類性能卻提升不多,使得最終的平均準確率與隨機抽樣的方法相差不大。隨著每個子集上需要判別的類別數的增多,各個主動學習算法在Binary Alphadigits數據集上的平均準確率都有不同程度的下降。但在子抽樣集包含3類樣本時,所有算法的準確率都達到了83%以上,相較于傳統主動學習算法直接處理這類樣本的實驗準確率有較大提升,證明本文提出的主動學習框架是有效的。

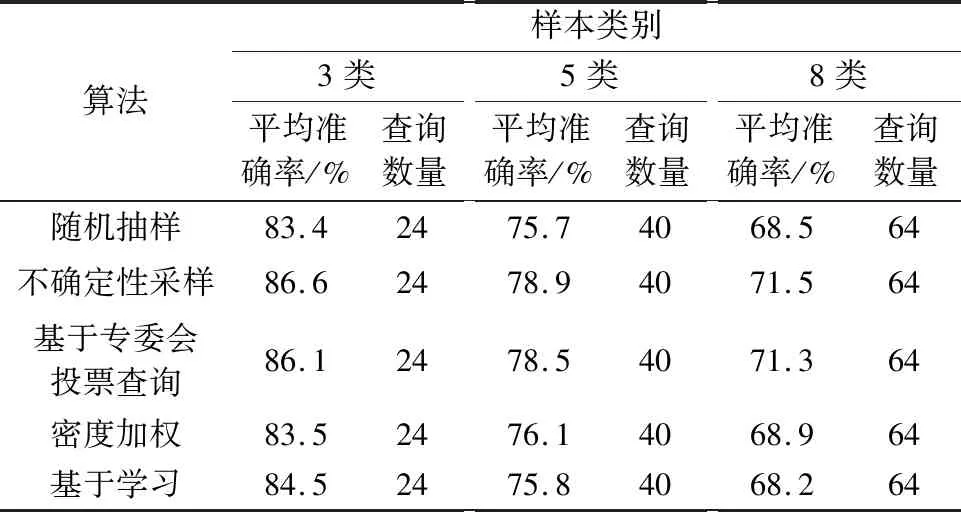
表1 Binary Alphadigits數據集實驗結果Table 1 Experimental results of Binary Alphadigits dataset

2.3.2 OMNIGLOT實驗結果

相較于Binary Alphadigits數據集,OMNIGLOT數據集具有更多的類別數和每類更少的樣本數,因此對于傳統的主動學習方法來說是一個更大的挑戰。不同算法在OMNIGLOT數據集上的性能曲線如圖5所示。每回合的查詢樣本數從p開始,到總樣本數的80%結束。從圖5中可以看出,在OMNIGLOT數據集上,隨著查詢次數的增加,各個算法的準確率均有不同程度的提高。基于專委會投票查詢的主動學習模型的平均性能最好,達到的平均準確率最高。基于密度加權的主動學習模型表現最差,低于隨機抽樣方法的準確率基線。

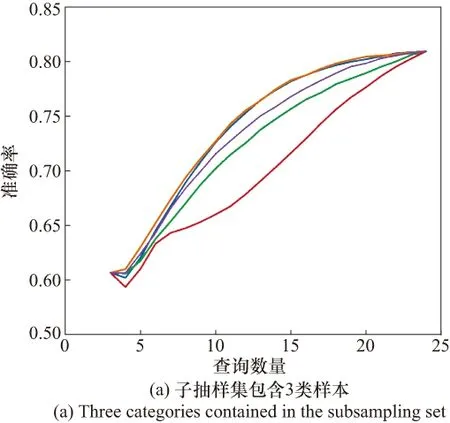
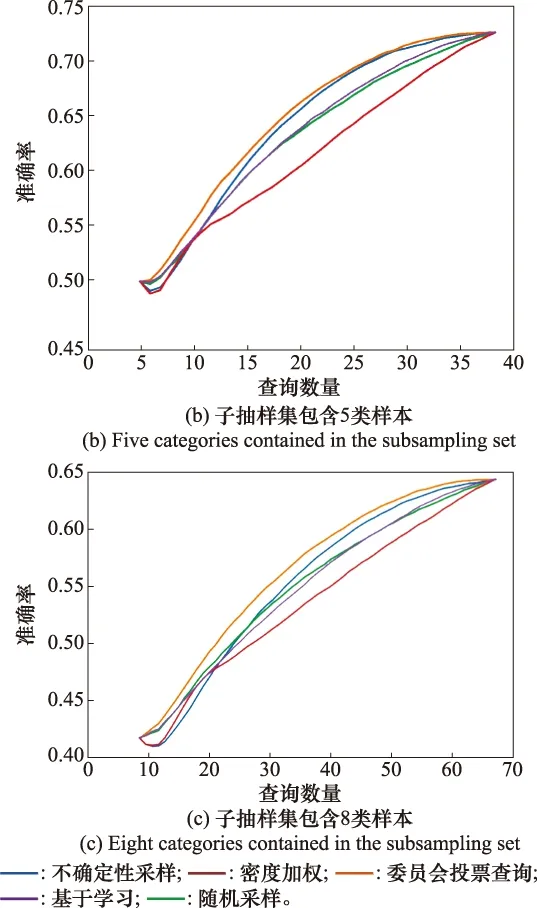
圖5 OMNIGLOT數據集的算法性能對比Fig.5 Algorithm performance comparison of OMNIGLOT dataset

OMNIGLOT數據集上各個算法的實驗結果如表2所示。

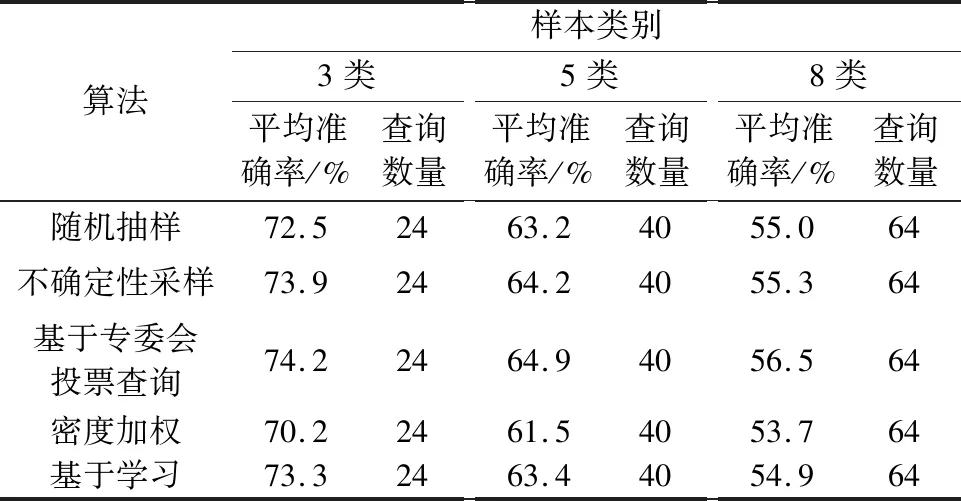
表2 OMNIGLOT數據集實驗結果Table 2 Experimental results of OMNIGLOT dataset

根據表2可知,基于專委會投票查詢的主動學習模型的平均性能最好,達到的平均準確率最高。基于密度加權的主動學習模型表現最差,低于隨機抽樣的主動學習方法的準確率基線。隨著每個子集上需要判別的類別數的增多,各個主動學習算法的平均準確率下降明顯。在子抽樣包含3類樣本時,所有算法的平均準確率都在70%以上,但在8分類問題中所有算法的平均準確率都低于60%,結合圖5,即使對整個測試集進行標注,以上幾種主動學習算法在測試集上的準確率也不超過65%。結果表明,由于數據集過大且有效信息不足,不依靠本文提出的標準框架,單純以傳統主動學習算法將根本無法解決這類問題。另外,本文提出的主動學習框架雖然能夠一定程度上解決傳統主動學習算法難以處理大規模數據集多類別分類問題,但框架性能對p值較為敏感,只有合適的p值才能較大程度提高算法性能。

2.4 算法性能對比分析

在第2.3節充分展示本文算法性能的基礎上,本節從實驗準確率和耗時兩個方面,對比SBAL算法和原始主動學習算法之間的性能差異。對比實驗采用與第2.3節相同的數據集作為實驗對象,實驗的基本設置不變,區別在于主動學習的采樣策略是否使用本文所提出的子抽樣方法。

2.4.1 Binary Alphadigits實驗

在分別使用原始采樣策略和子抽樣采樣策略條件下,不同算法的實驗準確率以及總耗時，如表3所示。其中，子抽樣策略取p=3,抽取100個子集。

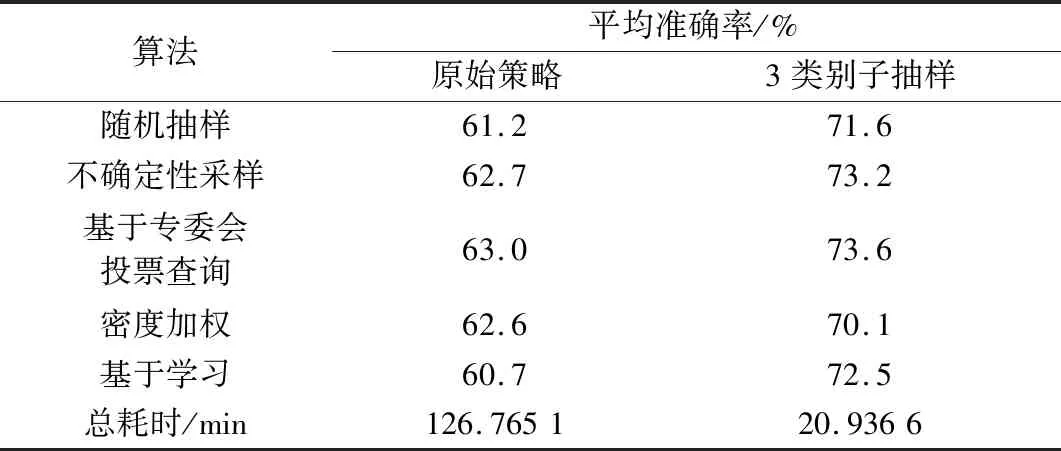
表3 Binary Alphadigits數據集對比實驗結果Table 3 Comparative experimental results of Binary Alphadigits dataset

由于抽取100個子集后,子抽樣策略的實驗準確率已經高于原始策略,因此,為突出耗時差異,抽取子集數不采用第2.3節實驗的10 000個。表3數據可以反映出,SBAL算法對比傳統主動學習算法,性能有所提高,準確率提升12%～19%不等,總耗時縮減為原始算法的1/5左右。相比較而言,本文算法的耗時相當可觀,在同樣的實驗條件和設置下,算法性能均優于原始算法。

2.4.2 OMNIGLOT實驗

由于該數據集樣本數量過大,且每個樣本是784維的向量,經實驗發現,處理這種規模的數據,使用傳統主動學習的方法已經超出了計算機最大的處理能力。因此,為通過具體實驗數值展示算法優劣性,不斷減少數據集規模,最終發現當數據集規模刪減為100類樣本,共2 000個樣本時,原始算法才能正常運行。具體實驗結果如表4所示。在OMNIGLOT數據集上的實驗充分證明,當數據量過大時,傳統主動學習根本無法有效運行,然而使用SBAL算法可以正常運行。通過刪減數據集規模,雖然傳統算法能夠勉強運行,但結果顯示其準確率已經十分低,根本無法用于實際問題。相較而言,SBAL算法準確率提高了123%～195%,耗時縮減為原始策略的1/50。

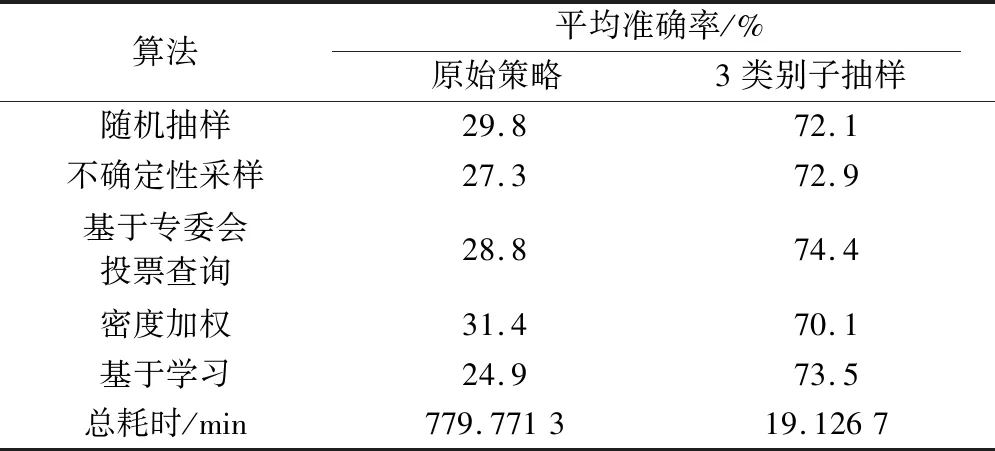
表4 OMNIGLOT數據集對比實驗結果Table 4 Comparative experimental results OMNIGLOT dataset

2.4.3 性能對比分析

對比實驗的目的,在于比較采用SBAL算法框架和原始算法之間的性能差異。突出本文算法在同樣的實驗條件和設置下,算法性能的優越性。經過實驗驗證,當處理數據規模巨大,分類數量繁多的問題時,傳統主動學習算法不僅需要更強的計算能力,還會耗費大量的計算時間,甚至不能有效運行,且準確率幾乎不可以接受。當采用本文所提出的SBAL算法框架后,實驗準確率有較大提升,并且實驗耗時有顯著縮減。

2.5 p取值分析

為了分析p取值對實驗結果的影響,考察了在不同p值選擇下,實驗準確率的變化。

如圖6所示,從整體上看,實驗準確率會隨著p值的增大而波動降低。當p取值接近2時,不同算法的準確率普遍最高,大約為85%。因為子抽樣類別數為2時,即使無監督聚類結果不準確,也不會帶來大量的錯誤分類樣本,有利于主動學習算法對樣本的準確標注。但隨著p值增加,無監督聚類的準確率對實驗結果的影響顯著增加,因為聚類算法的性能缺陷,必然會引入錯誤分類的樣本,而樣本類別數增加也會使得主動學習算法更難準確標注樣本類別,綜合兩個因素,實驗準確率的確應該呈遞減趨勢而變化。

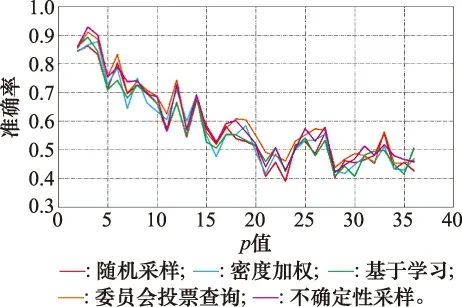
圖6 Binary Alphadigits數據集下p值對實驗準確率的影響Fig.6 Influence of the p-value on the accuracy of experiment in the Binary Alphadigits dataset

圖7所示是OMNIGLOT數據集下,實驗準確率的變化趨勢圖。在OMNIGLOT數據集上的實驗結果更為明顯,當p值初始取最小值2時,實驗準確率最高,大致為85%。隨著p值增大,實驗準確率迅速降低,當p=5時,準確率已經降為60%左右。當p=25時,準確率降低速度趨緩,并大致在30%～40%波動。剖析導致實驗準確率如此變化的原因,和圖6實驗大同小異。由于p值較小時,即便無監督聚類結果存在偏差,對主動學習標注來說,并不會造成過大影響。但隨著p值增大,既會導致無監督聚類錯誤標注的樣本對實驗準確率影響增大,又會因為類別數增多,導致主動學習階段本身錯誤率增加。

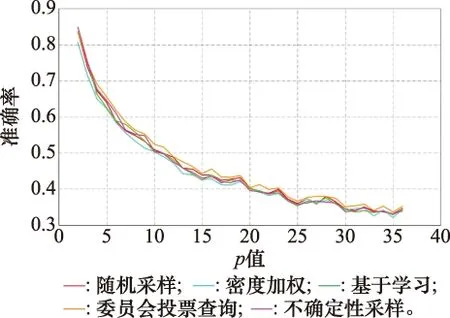
圖7 OMNIGLOT數據集下p值對實驗準確率的影響Fig.7 Influence of the p-value on the accuracy of experiment inthe OMNIGLOT datasets

3 結 論

針對傳統主動學習方法在多類別數據集標注上的應用局限性,本文提出了面向多類別數據分類問題的子抽樣主動學習方法。該方法提出一個標準框架,將無監督聚類算法、子抽樣和主動學習方法進行整合,通過對聚類結果子抽樣,縮小單次計算的數據集規模,進而簡化主動學習方法的處理難度。所提方法在Binary Alphadigits和OMNIGLOT數據集上進行了實驗檢驗,結果證明,本文提出的SBAL標準框架可以有效處理大規模數據集多類別分類問題,算法性能對比實驗結果顯示,SBAL算法的實驗性能高于傳統主動學習算法,但框架性能對p值敏感,現有實驗結果表明,當p值較小時,算法平均準確率更高。

本文方法具有通用性,可以更換聚類算法和主動學習算法,對不同數據集也有較好的泛化性能,適用于多種實際應用背景,應用前景廣泛,能夠有效化解訓練數據標注缺失的問題。但仍有亟待解決的問題和需要研究的方向:

(1) 本文框架只是對傳統主動學習算法的部分改進,沒有從本質上突破其精度上限。所以,如何構建全新的算法模型,解決數據標注難題,仍將是未來需要研究的方向。

(2) 本文實驗雖然得出了框架性能受p值影響的定性結論,但還未給出其定量關系,研究p值對實驗性能影響的定量關系,將會有效推動本文框架的實用性。

(3) 本文框架是解決大規模數據集多類別分類問題的一次有效嘗試,雖然相較于傳統主動學習算法,性能有了較大提升,但從其平均準確率看,還達不到工程應用的標準,完善算法流程,進一步提高實驗準確率,也將是下一步的研究方向。