大規模MIMO系統中分布式壓縮感知LMMSE信道估計

李貴勇,于 敏,余永坤

(重慶郵電大學通信與信息工程學院,重慶 400065)

0 引 言

在移動通信領域,需要通過增加系統容量和頻譜效率的新技術來滿足用戶不斷增長的數據速率需求,現有的長期演進系統的一項關鍵技術——多輸入多輸出(multiple input multiple output,MIMO)可以在不增加任何無線帶寬的情況下提高系統容量[1]和系統可靠性,但MIMO技術無法滿足未來移動通信系統的需求。大規模MIMO技術可以通過在基站(base station,BS)側配置大量天線,在極大程度上增加系統容量,由于大規模MIMO帶來的高頻譜效率和高能效[2],被視為未來5G無線通信系統的關鍵技術之一。在大規模MIMO系統中,準確有效的信道估計是一個至關重要且棘手的問題,因為隨著天線的增加,需要估計的信道參數的數量非常大,因此帶來了極高的計算復雜度。線性最小均方誤差(linear minimum mean square error,LMMSE)算法作為經典信道估計算法,由于其良好的抗噪性能已被廣泛用于傳統無線通信系統中。但是,要在5G大規模MIMO系統中使用LMMSE信道估計算法面臨的挑戰是:難以獲得信道自相關矩陣,并且大規模天線帶來的計算復雜性極高[3]。因此,如何在信道估計的性能和算法復雜度之間保持最佳平衡至關重要。

為了優化LMMSE算法,文獻[4]提出了一種基于離散傅里葉變換(discrete Fourier transform,DFT)的LMMSE算法,該算法利用DFT屬性估計信道相關矩陣,減少了參數計算量,以較低的計算復雜度達到了較高的信道估計性能。盡管很多專家學者為降低傳統信道估計復雜度和提高傳統信道估計算法的性能已進行了許多努力,但所有這些方法都限于Nyquist-Shannon定理,在大規模MIMO系統中會導致極高的導頻開銷以及極高的計算復雜度。

Donoho[5]提出了壓縮感知(compressed sensing,CS)理論,用于稀疏信號處理，近年來已被廣泛用于大規模MIMO系統的稀疏信道估計。CS理論適用于減少信道估計所需的導頻開銷[6-7]，是因為與大量發射天線相比,BS和用戶之間的大量MIMO信道顯示出有限的散射和小角度擴展,使得無線信道可以在虛擬角域中以稀疏形式表示[8-9]。文獻[10]考慮了一種多用戶場景,其中信道矩陣在地理上相鄰的用戶之間共享一些公共散射體和公共稀疏性，提出了一種聯合正交匹配追蹤恢復算法,以利用多用戶信道矩陣中的隱藏聯合稀疏性。文獻[11]考慮了用戶分組策略,通過利用波束塊稀疏性來聯合恢復用戶組的信道矩陣。文獻[12]利用信道稀疏性信息和支持集在連續時隙中保持不變的特性,考慮稀疏信道的先驗支撐集信息,進一步研究了大規模MIMO系統中具有時間相關性的稀疏信道估計,以減少所需的導頻訓練開銷。文獻[13]通過利用信道統計信息在連續幀的緩慢變化特性,提出了一種CS輔助方法來減少導頻開銷,該方法同時利用了最小二乘(least squares,LS)算法和CS算法,但是僅考慮了窄帶信道。文獻[14]對于頻分雙工(frequency division duplex,FDD)系統提出了一種基于空間通用稀疏性的自適應信道估計和反饋方案,該方案可以自適應地進行調整。在文獻[15]中,當通道稀疏度未知時,首先通過設置適當的閾值并找到最大后向差的位置來選擇原子,然后使用正則化方法提高原子選擇的準確性。文獻[16-19]在非正交多址接入系統中引入了LMMSE信道估計算法。文獻[17]利用上下行鏈路角度域互易性,基于上行鏈路訓練先驗支撐集,利用支撐集信息提出分布式CS(distributed CS,DCS)信道估計算法。

為了降低傳統LMMSE算法的復雜度并提高純CS理論估計算法的性能,本文提出一種DCS-LMMSE信道估計算法。第一步,利用信道在連續幀之間變化緩慢和子載波之間傳播相似共享角度域稀疏性的特性,提出導頻混合訓練及混合估計結構。對于信道初始估計，根據支撐集信息將接收的信號分為稀疏部分和密集部分,結合LS和CS理論分別估計當前幀角度域信道矢量的密集部分和稀疏部分,并將角度域信道矢量轉換為頻域信道矢量。第二步,將初始信道矩陣與信道相關矩陣相乘,并利用奇異值分解(singular value decomposition,SVD)代替信道相關矩陣求逆,進一步降低算法復雜度。

1 系統模型

1.1 通信模型

本文采用的典型FDD大規模MIMO系統模型如圖1所示。

圖1 系統模型Fig.1 System model

一個小區內,BS側部署M根天線,分布U個單天線用戶,且M?U。系統采用的載波調制方式為正交頻分復用(orthogonal frequency division multiplexing,OFDM)調制,導頻數為N。每幀包含T個時隙,對于第j個時隙用戶u的第k個子載波的接收信號為

(1)

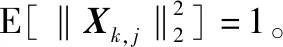
(2)

式中,yu,k∈C1×T,Xk∈CM×T,Nu,k∈C1×T分別表示T時隙內用戶u子載波k的接收信號、導頻序列和信道噪聲。

1.2 信道模型

假定信道多徑數為L,第k個子載波上BS和用戶u相關聯的下行鏈路信道[13]可以表示為

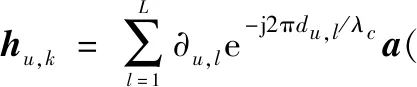
(3)

(4)

式中,d為BS側天線之間的間隔。可以在角度域將式(3)中的下行鏈路頻域信道進一步表示為

(5)

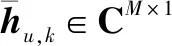
(6)

結合式(3)～式(5)角度域信道向量可以表示為

(7)

(8)

(9)

(10)

(11)

(12)

(13)

S=|Ωu,k|C?M

(14)

Ωu,1=Ωu,2=…=Ωu,N

(15)

圖2 角度域共稀疏性Fig.2 Co-sparseness of angle domain

1.3 時域信道模型

本節對于時域信道模型建模,在系統幀t中給定用戶u的信道矢量[13]表示為

(16)

(17)

由于信道統計信息在連續兩幀之間變化緩慢,則有

(18)

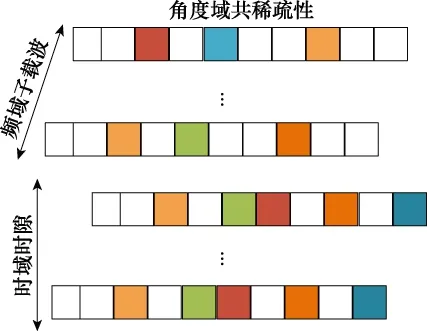
圖3 子載波共享不同時隙支撐集變化Fig.3 Subcarrier sharing support set changes in different time slots

2 DCS-LMMSE信道估計算法

2.1 導頻結構構造

利用上述特征可以將導頻構造為密集部分導頻和稀疏部分導頻,分別用于密集部分信道估計和稀疏部分信道估計。t幀導頻構造可以表示為

(19)

(20)

(21)

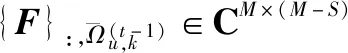
2.2 DCS初始信道估計算法

DCS初始信道估計是一種混合估計結構,初始先驗支撐集信息在初始同步或失步時基于FDD上下行鏈路角度域互易性,根據上行鏈路導頻序列估計反饋給用戶,并在每幀更新并傳遞給下一幀。基于先驗支撐集信息,可將用戶側頻域第k個子載波處在T時隙內接收到的信號分為兩部分,即

(22)

2.2.1 密集部分初始信道估計算法

(23)

(24)

2.2.2 稀疏部分初始信道估計算法

(25)

結合式(21)和式(25)，可表示為

(26)

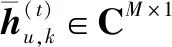
(27)

對于求解式(27)中提出的優化問題,基于貪婪算法進行信號恢復,詳見算法1。

算法1 基于CS理論稀疏部分初始信道估計算法輸入:接收信號Y(t)k,s,觀測矩陣Φ(t)k,s∈C(T-S)×(M-S)步驟1 初始化:殘差向量r0k=(Y(t)k,s)T∈C(T-S)×1,支撐集Γ0=?,角度域信道矢量 hk=0∈C(M-S)×1,迭代次數i=1步驟2 計算分布式相關值:Cik=(Φ(t)k,s)Hri-1k步驟3 計算最大相關系數索引:γ=argmax1≤q≤M∑Nk=1|{Cik}q|2步驟4 更新支撐集:Γi=Γi-1∪γ步驟5 計算分布式LS估計值:{^hik}Γi=({Φ(t)k,s}H:,Γi{Φ(t)k,s}:,Γi)-1{Φ(t)k,s}H:,Γi(Y(t)k,s)T步驟6 分布式殘差更新:rik=(Y(t)k,s)T-Φ(t)k,shik步驟7 迭代次數更新:i=i+1步驟8 停止迭代條件:i>Sn輸出:信道估計值1ρ hik

首先初始化迭代過程中使用的參數;接著進入迭代過程,每次迭代針對不同子載波k計算分布式相關值,并根據殘差矢量與觀測矩陣的相關性,將最大相關值索引存儲在索引集中,因為不同子載波之間的公共稀疏性,不同子載波共用此索引集;最終當滿足迭代終止條件時退出迭代,輸出角度域信道系數估計值。

通過上述描述,第k個子載波處的角度域初始信道估計值表示為

(28)

(29)

2.3 DCS-LMMSE信道估計算法整體描述

在大規模MIMO系統中隨著天線數量的急劇增加,傳統LMMSE算法帶來了不可達的復雜度,本文結合傳統的LMMSE算法與CS理論,意在降低傳統LMMSE算法的復雜度和提高純CS理論估計算法的性能。

2.3.1 傳統的LMMSE信道估計

傳統的LMMSE算法在最小均方誤差(minimum mean square error,MMSE)的基準上用數學期望E[(XXH)-1]來代替求逆矩陣(XXH)-1,傳統的LMMSE算法可以表示為

(30)

信道自相關矩陣RHH∈CN×N為信道功率延遲譜(power delay profile,PDP)的統計量,在較長時間內是固定的,如果傳輸的導頻符號映射到相同的星座圖中,σ2(XHX)-1可以用其期望表示為

(31)

式中,I∈CN×N為單位陣;信噪比(signal to noise ratio,SNR)為E{|Xk|2}/σ2;Xk為發送符號;常量β=E{|Xk|2}E{|1/Xk|2},由調制信號的星座圖決定。結合式(30)和式(31)，傳統的LMMSE信道估計算法可以表示為

(32)

式中,信道自相關矩陣為

RHH=E{HHH}=[rm,n]

(33)

(34)

式中,m和n表示導頻子載波的位置;τmax表示信道歸一化最大多徑時延;τrms表示信道歸一化均方時延。

2.3.2 DCS-LMMSE信道估計

利用SVD代替相關矩陣求逆來降低算法復雜度,首先將信道自相關矩陣RHH分解為

RHH=UΛUH

(35)

(36)

令RHiHi為發射天線i的信道自相關矩陣。將大規模MIMO系統中所有發射天線的信道自相關矩陣整合為

(37)

式中,RHHtotal∈C(M×N)×(M×N)為大規模MIMO系統中所有發射天線的信道自相關矩陣。對于所有天線整體信道矩陣為

(38)

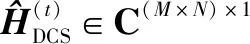
圖4 DCS-LMMSE算法流程圖Fig.4 Flowchart of DCS-LMMSE algorithm

2.3.3 主要系統性能參數分析

接收端信道向量的估計值可以表示為

(39)

(40)

歸一化MSE(normalized MSE,NMSE)單位為dB,可表示為

NMSE=10lg(MSE)

(41)

接收端得到的信道向量估計值后對接收信號進行最大似然檢測,最大似然檢測結果為

(42)

式中,xk表示在子載波k上的發送信號;yk為子載波k上的接收信號;C表示正交振幅調制(quadracture amplitude modulation,QAM)的狀態空間。本文用誤比特率(bit error ratio,BER)作為衡量數據傳輸精確性的指標。在使用QAM調制的基帶系統中,系統理論BER[18]可以表示為

(43)

N0=var(nk-hexk)=var(nk)+var(hexk)

(44)

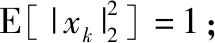
(45)

結合式(43)和式(45)可以將BER進一步推導為

(46)

BER在實際系統仿真中,也可以用一定時間內系統接收的數字信號中發生差錯的比特數biterror與系統接收的數字信號總比特數bittotal的比值計算。

(47)

2.4 計算復雜度分析

由于信道在連續幀之間變化緩慢,Sn的值應該較小,則本文算法復雜度可近似為Ο(SnN(T-S)(M-S)+NS+MN)。傳統的LMMSE信道估計算法復雜度為Ο(2MN3)。算法復雜度如表1所示,其中未包含信道相關矩陣的計算,原因是信道相關矩陣的計算兩種算法相同,算法對比時可將此省略。

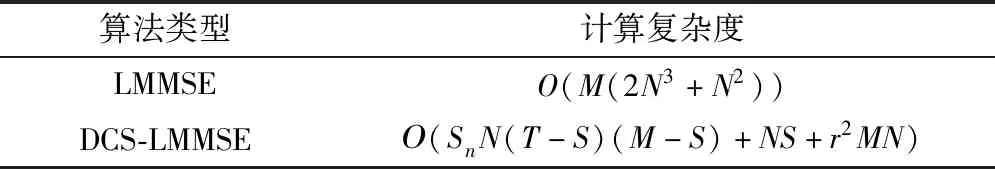
表1 算法復雜度Table 1 Algorithm complexity

從表1可以看出,由于信道在連續幀之間變化緩慢,Sn的值較小,因此傳統LMMSE算法主要計算復雜度為Ο(2MN3),主要來源于信道相關矩陣相乘和求逆的計算。本文所提算法主要計算復雜度為Ο(SnN(T-S)(M-S)+NS+r2MN)。由于大規模MIMO系統中BS側天線數M很大,可見本文所提算法相較于傳統LMMSE算法有效地提高了計算效率,降低了算法復雜度。

3 仿真結果及分析

3.1 仿真場景及參數設置

在本節中,將通過Matlab仿真平臺對本文提出的DCS-LMMSE算法進行仿真驗證。現將仿真場景設置如下,在一個多用戶-MIMO(multi-user-MIMO,MU-MIMO)場景下,每個小區中心設置一個部署了M根天線的BS,小區內隨機分布著U個單天線用戶,使用第3代合作伙伴計劃(3rd generation partnership project,3GPP)的空間通道模型(spatial channel model,SCM),設置角度域稀疏系數為8,仿真參數如表2所示。

表2 仿真參數設定Table 2 Simulation parameters setting

3.2 仿真結果分析

大規模MIMO系統中,BS與用戶位置分布如圖5所示。每個小區中心分布著一個部署著M根天線的BS,在小區內U個用戶位置服從隨機分布。

圖5 大規模MIMO BS與用戶位置分布Fig.5 Location distribution of massive MIMO BS and users

圖6為角度域信道稀疏性圖,仿真設置基站端部署128根天線,信道在角度域的稀疏性為8,其中非0角度基如圖6中所示。圖7所示為LMMSE,DCS-LMMSE,DCS以及正交匹配追蹤(orthogonal matching pursuit,OMP)4種不同的信道估計算法的NMSE隨著SNR的變化關系。從圖7中可見,在SNR較低的情況下,所提DCS-LMMSE算法性能優于DCS算法,在SNR=5 dB時,DCS-LMMSE算法NMSE相較于DCS算法約有3 dB的性能提升。由于低SNR情況下,DCS-LMMSE算法在DCS算法的基礎上添加了LMMSE估計,可近似看作在DCS算法結果的基礎上添加了一個微納濾波器,降低噪聲對系統性能的影響。隨著SNR的增加,噪聲對系統的影響減少,DCS算法的性能逐漸接近DCS-LMMSE算法性能,并且DCS算法與DCS-LMMSE算法性能都逐漸接近LMMSE算法。盡管本文所提算法性能略差于LMMSE算法,但是較于LMMSE算法顯著提高了計算效率,以可接受的性能成本換取了可觀的計算效率增益。仿真結果表明，DCS-LMMSE算法的抗噪性能優于純CS理論的信道估計算法,更有利于解決大規模MIMO系統中的導頻污染問題。

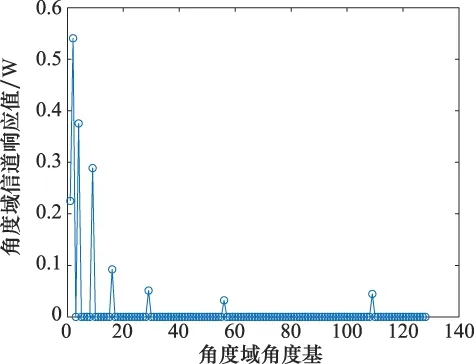
圖6 角度域信道稀疏性Fig.6 Channel sparsity in angle domain

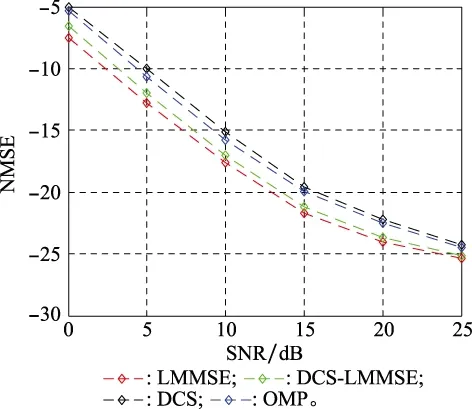
圖7 不同信道估計算法的NMSE隨SNR變化關系Fig.7 Variation of NMSE with SNR for different channel estimation algorithms

使用不同信道估計算法時系統的BER與SNR的關系如圖8所示。從圖8中可以看出,當SNR=5 dB時,DCS-LMMSE算法的BER相較于DCS算法約降低了47.9%。當BER=1×10-2時,DCS-LMMSE算法相較于DCS算法約提升了3 dB。一方面,本文所提DCS-LMMSE算法相較于基于純CS理論的DCS算法在BER方面取得了更好的系統性能,體現出本文所提算法具有更好的抗噪性能。另一方面，本文所提算法最接近使用傳統LMMSE算法的系統BER,但相比于傳統LMMSE算法,有效地降低計算復雜度，并且在SNR=25 dB時,本文所提算法系統BER約為3.43×10-5,體現了更高的可靠性。

圖8 不同信道估計算法的BER隨SNR變化關系Fig.8 Variation of BER with SNR for different channel estimation algorithms

使用不同信道估計算法均衡后，16QAM系統接收信號星座圖對比如圖9所示。可以看出在SNR=21 dB時,DCS-LMMSE算法性能接近于傳統LMMSE算法性能,并且相比于DCS算法,可以以更高質量恢復數據。另一方面，相比于傳統LMMSE算法,DCS-LMMSE算法以可接受的性能損失換取了可觀的計算效率增益,有效地降低計算復雜度。

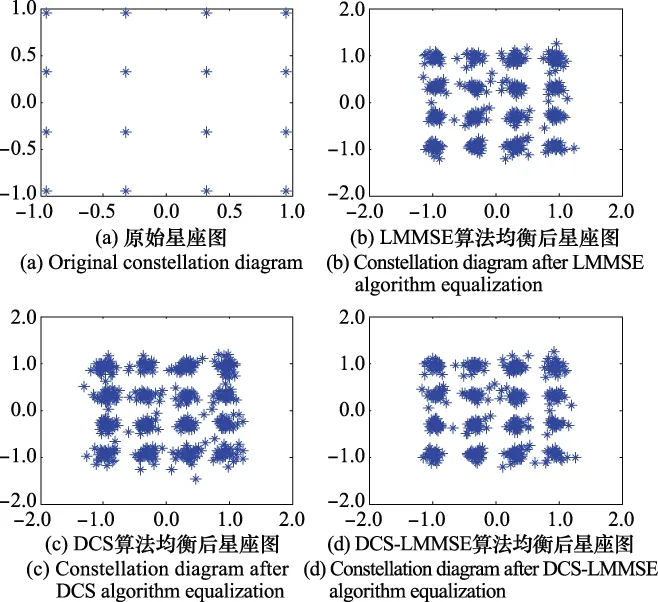
圖9 不同信道估計算法均衡后星座圖對比Fig.9 Comparison of constellation diagrams after equalization of different channel estimation algorithms

4 結 論

本文研究了針對大規模MIMO系統的信道估計方案。該方案結合LMMSE算法與DCS算法，利用信道在連續幀之間變化緩慢和子載波之間傳播路徑相似共享角度域稀疏性的特性,基于先驗支撐集信息將接收信號分為稀疏部分和密集部分,結合LS算法和CS算法進行初始信道估計,降低了CS理論中主要的迭代計算復雜度,最后采用SVD代替信道相關矩陣求逆,進一步降低DCS-LMMSE算法的復雜度。所提算法與傳統LMMSE算法相比，明顯降低了計算復雜度,與純CS理論信道估計算法相比也具有更好的性能。