基于SCMA和卷積編碼的聯(lián)合檢測譯碼算法

趙宏偉,劉春陽,許 利,羅 霞

(1.西北工業(yè)大學電子信息學院,陜西 西安 710072;2.北京遙測技術(shù)研究所,北京 100076)

0 引 言

測控是保障衛(wèi)星通信系統(tǒng)正常運行的重要環(huán)節(jié)[1]。近幾年衛(wèi)星星座及衛(wèi)星數(shù)量不斷增多,特別是低軌星座數(shù)目的爆發(fā)式增多,對衛(wèi)星測控系統(tǒng)提出了更高的要求。地基測控系統(tǒng)需要建設分布范圍廣、數(shù)量多的地面測控站,而天基測控具有高覆蓋率和多目標服務的能力,因而利用近地軌道衛(wèi)星或者地球同步軌道衛(wèi)星對低軌衛(wèi)星星座進行測控,是當前衛(wèi)星中繼測控研究領(lǐng)域的重要內(nèi)容。目前,衛(wèi)星系統(tǒng)的測控和通信方式主要是采用碼分多址接入(code division multiple access,CDMA)技術(shù),比如現(xiàn)隸屬美國軍方的Iridium、Globalstar、Aries等小衛(wèi)星系統(tǒng),以及美國的跟蹤與數(shù)據(jù)中繼衛(wèi)星系統(tǒng)(tracking and data relay satellite system,TDRSS)等都采用了CDMA技術(shù)[2]。隨著大量LEO衛(wèi)星星座的組網(wǎng)運行,同時接入系統(tǒng)進行通信的衛(wèi)星數(shù)量將大大增加,CDMA系統(tǒng)的多址干擾會嚴重影響系統(tǒng)容量。因此，急需研究新的多址接入技術(shù)來提升大過載衛(wèi)星通信、測控服務的能力。

稀疏碼分多址接入(sparse code multiple access,SCMA)[3-4]是華為公司提出的一種碼字域非正交多址技術(shù),已經(jīng)作為一種空口技術(shù)在5G移動通信中得到了廣泛的應用。SCMA技術(shù)作為一種新型的非正交多址技術(shù),因其能夠提供超過傳統(tǒng)信道容量極限的接入能力而受到國內(nèi)外學者的廣泛關(guān)注。SCMA技術(shù)具有高速率、低延遲和最大頻譜效率等特點,適用于大規(guī)模衛(wèi)星系統(tǒng)的通信[5-6]。SCMA技術(shù)是基于低密度擴頻多址接入(low-density-signature multiple access,LDS-MA)技術(shù)擴展而來,在發(fā)射過程中將傳統(tǒng)數(shù)字調(diào)制與低密度擴頻技術(shù)相結(jié)合,將多用戶信息通過映射矩陣映射到少量傳輸信道中,在空間傳輸過程中進行疊加。在接收端,接收到同一信道中的多用戶信息后,進行多用戶檢測,恢復出不同用戶的發(fā)送信息,從而得到高于傳統(tǒng)方式的用戶承載力,提升當前衛(wèi)星測控系統(tǒng)的容量。在接收端采用SCMA譯碼常用算法消息傳遞算法(massage passing algorithm,MPA)[7-8]能夠在保證算法復雜度較低的前提下實現(xiàn)有效譯碼。因此,考慮在衛(wèi)星測控中應用SCMA技術(shù)以提高用戶承載能力,并且采用MPA及其改進算法進行多用戶檢測。

針對MPA實現(xiàn)復雜度較高的問題,文獻[9]采用局部邊緣的方法,提出了一種部分邊緣化MPA(partial margina-lization MPA,PM-MPA)。PM-MPA在每次迭代中只選取部分節(jié)點進行譯碼判決,雖然降低了算法復雜度,但由于選擇的隨機性導致系統(tǒng)誤碼率較高。當MPA在執(zhí)行節(jié)點消息的迭代更新過程時,需要遍歷所有的疊加碼字星座點(superposed constellation point,SCP),而文獻[10]提出的基于球形譯碼的MPA(sphere decoding MPA,SD-MPA)在譯碼消息傳遞的過程中,將接收到的疊加碼字星座點與理論星座點位置進行計算比較,只保留球形半徑內(nèi)的星座點,減少搜索點數(shù),提高迭代速度。通過使用球形譯碼的方法,能夠有效減少搜索星座點數(shù),帶來算法復雜度的降低,但很難動態(tài)確定有效球形半徑,同時每次信息更新后,各個用戶的收斂程度也會有所差別,以致最終譯碼性能不穩(wěn)定。文獻[11]提出采用子圖的迭代方式來降低復雜度,稱為動態(tài)子圖MPA(dynamic subgraph MPA,DS-MPA)。DS-MPA將原因子圖進行分割,每次迭代時只迭代部分因子圖,而且同時實現(xiàn)不同用戶迭代次數(shù)的合理調(diào)整,將計算資源合理分配,從而降低算法的整體復雜度。但同樣雖然該算法復雜度進行了有效降低,但譯碼性能仍然很難滿足當前衛(wèi)星測控高可靠性的要求。

信道編碼可以保障數(shù)字通信系統(tǒng)的可靠性傳輸。在衛(wèi)星測控系統(tǒng)中,由于信道衰落、噪聲、干擾的存在,會導致接收端出現(xiàn)譯碼錯誤的情況,因此使用信道糾錯編碼技術(shù)是衛(wèi)星測控系統(tǒng)中的一個重要環(huán)節(jié)[11]。信道卷積編碼技術(shù)是一種性能較好的糾錯編碼技術(shù),其在衛(wèi)星導航與通信中有著廣泛應用。卷積碼的移位編碼器由m級移位寄存器和u個模2加法器組成。該編碼器同時允許u位比特輸入,v位比特輸出,編碼器的輸出比特不僅取決于正在輸入的u比特信息,還取決于這之前的m比特信息[12]。擁有這樣編碼器結(jié)構(gòu)的卷積碼稱為(v,u,m)卷積碼。關(guān)于卷積碼常用的3種譯碼算法分別是:序列譯碼、門限譯碼和概率譯碼。其中,概率譯碼采用最大似然譯碼的原則,將接收序列與所有可能碼序列進行對比,選擇似然概率最大的一個碼序列,作為譯碼結(jié)果輸出,維特比譯碼是概率譯碼中最為常用的一種方法[13-14]。

基于此,本文將卷積編碼引入SCMA系統(tǒng),并采用子圖的迭代方式,提出基于似然信息交換的SCMA和卷積編碼的聯(lián)合檢測譯碼(joint detection and decoding,JDD)方案。該方案利用SCMA超過傳統(tǒng)信道容量極限的特性,可有效提高當前天基衛(wèi)星測控系統(tǒng)的用戶容量,滿足當前低軌衛(wèi)星測控海量用戶的需求。另外利用發(fā)送信息之間的相關(guān)性,進行對數(shù)域的似然信息交換,在保證算法復雜度較低的前提下,提高了譯碼算法的可靠性,可有效提高系統(tǒng)誤比特性能。

1 SCMA系統(tǒng)模型

1.1 發(fā)送端模型

SCMA編碼原理[15-16]如圖1所示,這里以6個用戶在4個信道上傳輸為例來說明,系統(tǒng)信道過載率為150%,即可將原測控系統(tǒng)用戶容量提高一半。每個用戶采用4點星座圖進行調(diào)制,不同用戶有不同碼本,每個碼本是一個4×4的復數(shù)矩陣,其中矩陣的行表示信道,矩陣的列表示碼字。每個用戶每次傳輸2比特信息,包含4種可能的值,分別對應4個碼字,用戶發(fā)送的二進制比特為00～11時分別對應用戶碼本的第1～4列。

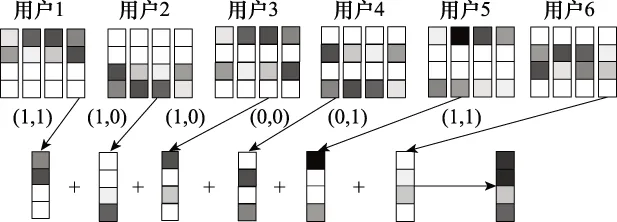
圖1 發(fā)送端模型Fig.1 Sender model

圖1所示6個用戶傳輸信息為11、10、10、00、01、11,對應各用戶各自碼本的第4、3、3、1、2、4列碼字,4個信道上的星座點分別進行相加,形成疊加碼字星座點。對于碼本的每一列而言,其具有稀疏性,包含零項和非零項,零項表示用戶在該信道上不傳輸信息,非零項表示用戶在該信道上傳輸信息[17]。為了表示方便,采用F矩陣來表示這樣一種結(jié)構(gòu),圖1對應的F矩陣為

(1)

式中,F4×6表示6個用戶在4個信道上傳輸時的映射矩陣;Fn,k表示矩陣F中的第n行第k列的元素;sn,k表示用戶k在信道n上傳輸?shù)男亲c數(shù)值。如由Fn,1可知,用戶1實際上只在信道1和信道2上傳輸信號;由F1,k可知,只有用戶1、用戶3和用戶5在信道1上傳輸信號。經(jīng)過高斯信道傳輸后信道n上的接收信號可以表示為

(2)

式中,J表示用戶數(shù);hn,k表示信道n上用戶k的信道系數(shù);mk表示用戶k選擇的碼字;Cn,k(mk)表示用戶k采用碼字mk時,該碼字第n個值,即用戶k在信道n上實際傳輸?shù)男畔⒅?nn表示信道n上的噪聲信息。對于圖1中的信道1,從矩陣F可知,信道1上實際疊加的有效用戶數(shù)為3,信號經(jīng)過信道1傳輸時,當k=2,4,6時,Cn,k(mk)=0,信道1對應的接收信號可表示為

y1=h1,1C1,1(m1)+h1,3C1,3(m3)+h1,5C1,5(m5)+n1

(3)

1.2 接收端模型

在接收端,主要目的是從N個信道上恢復J個用戶的M種符號數(shù)據(jù)。本文采用MPA進行譯碼,首先假設每個用戶發(fā)送的符號概率相等,然后通過迭代的方式在功能節(jié)點(function node,FN)和變量節(jié)點(variable node,VN)之間不斷更新對用戶發(fā)送符號的估計,等到估計的用戶發(fā)送符號概率值收斂到固定值時,或者達到了最大迭代次數(shù)時,停止FN和VN之間的信息傳遞,譯碼輸出VN上用戶發(fā)送符號的估計[16]。

用Ifn→vk(mn k)表示功能節(jié)點fn向變量節(jié)點vk傳遞的消息,mn k表示消息的狀態(tài),共M種,即mn k∈{1,2,…,M},消息的傳遞可分別表示為:Ifn→vk(1),Ifn→vk(2),…,Ifn→vk(M)。用Ivk→fn(mn k)表示vk向fn傳遞的消息。MPA在功能節(jié)點和變量節(jié)點上的迭代過程通常分成兩個步驟,循環(huán)迭代這兩個步驟直至收斂或達到最大迭代次數(shù),兩個步驟可以簡單表示如下。

步驟 1FN上的消息更新為

(4)

(5)

式中,ξn表示與fn相連的VN集合;k∈ξn/{k}表示除去用戶vk之外的與fn相連的VN集合。f(yn|x[n])為接收信號的概率密度函數(shù)值,定義為

(6)

步驟 2VN上的消息更新為

(7)

式中,ξk表示與vj相連的FN集合;Kk為調(diào)節(jié)因子,使得公式成立:

(8)

上述兩步驟中有較多指數(shù)與乘法運算,可將其轉(zhuǎn)換到對數(shù)域中進行計算以降低運算復雜度[15]。

在經(jīng)過有限次迭代以后,VN接收到來自FN的消息即為用戶發(fā)送的信號的估計,并將其作為檢測結(jié)果送入判決模塊,其表達式為

(9)

式中,tmax為最大迭代次數(shù);矩陣Q是一個包含J行,M列的矩陣,存儲J個用戶所發(fā)送的M個信息的概率估計大小。

2 卷積編碼

2.1 編碼器結(jié)構(gòu)

本文使用(2,1,2)卷積編碼器,該編碼器結(jié)構(gòu)簡單,適用于大規(guī)模衛(wèi)星通信系統(tǒng)。發(fā)送端將每個用戶的輸入比特流信息經(jīng)過卷積編碼模塊,把1比特信息送入碼率為1/2的卷積碼編碼器中擴展成2個編碼比特。卷積編碼生成結(jié)構(gòu)如圖2所示。

圖2 卷積編碼器Fig.2 Convolutional coder

生成矩陣表達形式如下:

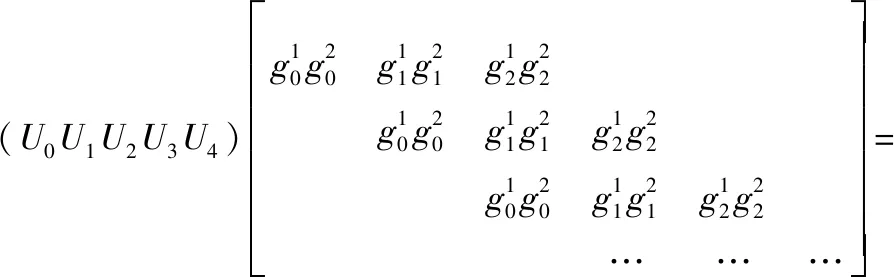
(10)

式中,U是信源發(fā)送信息;G是生成矩陣。g1=(1,0,1),g2=(1,1,1)對應于編碼器抽頭。

為了方便譯碼過程,人們通常使用狀態(tài)圖的表示方法在某時刻。將編碼器結(jié)構(gòu)中的移位寄存器中存儲的m比特信息組合起來,成為這個時刻的狀態(tài)。本文使用卷積碼編碼器結(jié)構(gòu)簡單,移位寄存器長度為2,所以共有4種狀態(tài)。當比特信息不斷輸入編碼器時,移位寄存器里的數(shù)據(jù)不斷更新,即編碼器狀態(tài)不斷變化。編碼器狀態(tài)轉(zhuǎn)移如圖3所示。

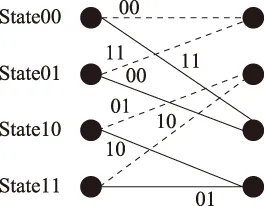
圖3 狀態(tài)轉(zhuǎn)移圖Fig.3 Diagram of state-transition

可以看到,某一特定狀態(tài)的下一狀態(tài)只有兩種可能。當前后兩狀態(tài)確定時,編碼器輸入也隨之確定,圖3中實線表示編碼器輸入為1,虛線表示編碼器輸入為0。狀態(tài)轉(zhuǎn)移線上標明的是當前時刻卷積編碼器的輸出。

2.2 維特比譯碼算法

與卷積編碼相對應的解碼算法維特比算法,是卷積碼在加性高斯白噪聲環(huán)境下的最優(yōu)譯碼算法,在移動通信和衛(wèi)星測控中被廣泛應用。在通信系統(tǒng)信道編碼與解碼的過程中,假設原始要發(fā)送信息為X,經(jīng)信道編碼后變?yōu)閅,然后經(jīng)過有噪信道傳輸以后,接收端接收到的信息為Z。維特比譯碼就是,根據(jù)接收到的信息Z,在譯碼網(wǎng)格中找到一條與Z似然概率最大,也就是擬合度最高的路徑作為糾錯結(jié)果,然后根據(jù)該路徑進行譯碼得到發(fā)送信息X的過程。

譯碼算法的具體實現(xiàn)是,當接收到一組比特信息時,在譯碼網(wǎng)格的每個狀態(tài)節(jié)點上,計算出接收信號的碼序列與籬笆圖上的各條分支路徑之間的距離,與前一個時刻路徑量度值相加,得到累計度量,然后比較所有以這個狀態(tài)為目的地的累計度量值,只保留一條具有最小距離的路徑作為幸存路徑,而將其他路徑放棄不用。下一時刻各路徑往后延伸一段,重復使用上述方法,保留上一時刻幸存路徑,繼續(xù)延伸路徑相加比較,循環(huán)此步驟直至輸出譯碼結(jié)果。整個譯碼過程可以用圖4的框圖來概括。

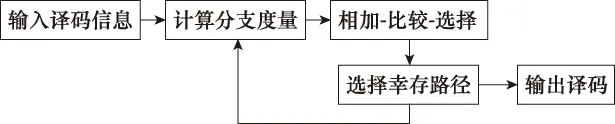
圖4 維特比譯碼Fig.4 Viterbi decoding

3 聯(lián)合檢測和譯碼算法

3.1 系統(tǒng)總體結(jié)構(gòu)

圖5即為基于卷積編碼的SCMA系統(tǒng)的整體框圖。首先,用戶比特流經(jīng)過卷積編碼,然后根據(jù)碼本將二進制比特信息映射到星座圖上,在使SCMA系統(tǒng)誤碼性能最優(yōu)的目標驅(qū)動下,在本節(jié)中,對于碼本,采用基于子集分割的TCM碼本[18-19];第2步,進行SCMA映射,將多用戶信息映射到對應傳輸信道中,仍然采用常用SCMA(6,4)模型,即6個用戶同時在4個信道中傳輸信息,每個用戶占據(jù)2個信道,每個信道中承載3個用戶;第3步,進行信息的物理發(fā)射,在發(fā)射過程中引入高斯白噪聲;第4步,接收端將接收到的信息進行SCMA多用戶譯碼,運用子圖動態(tài)調(diào)整用戶的整體更新次數(shù),并利用發(fā)送信息之間的相關(guān)性進行似然信息交換經(jīng)維特比譯碼得到譯碼結(jié)果;最后,將發(fā)送信息與譯碼結(jié)果進行對比得到整體誤比特性能。與單SCMA系統(tǒng)模型相比較,可以看出,聯(lián)合卷積編碼的SCMA系統(tǒng)是將SCMA譯碼得到的似然信息利用維特比譯碼算法進行糾錯,SCMA系統(tǒng)的其他模塊以及參數(shù)設置保持不變。

圖5 聯(lián)合卷積編碼的SCMA系統(tǒng)Fig.5 SCMA system with joint convolution coding

3.2 JDD算法

在MPA中,每次消息迭代以后,不同用戶的信息估計概率收斂性不同。采用DS-MPA可以動態(tài)生成原因子圖的子圖,該算法通過子圖更新信息,不必更新所有用戶信息。

經(jīng)過有限次迭代以后,VN接收到來自FN的消息即為用戶發(fā)送的信號的估計,表達形式為式(9),并將其作為檢測結(jié)果。然后計算并輸出待譯碼字的對數(shù)似然比(log-likelihood ratio,LLR),定義為

(11)

表示當某個比特為0時所有對應的碼字概率比上該比特為1時所有對應的碼字概率。

然后可以簡單地將輸出碼字LLRx進行硬判決后,將比特作為判決單位,漢明距離作為路徑度量值,送入維特比譯碼模塊進行糾錯[20-21]。

為進一步提高譯碼性能,可采用軟判決方式。軟判決不再利用LLR得到的比特信息,而是直接利用發(fā)送信號的估計概率值Qj(mn k),將其轉(zhuǎn)化為符號之間的距離,然后送入維特比譯碼模塊。使用消息傳遞算法中的直接輸出量,將譯碼器處理的最小信息單元從比特變?yōu)榉?能有效提高解碼誤比特率(bit error rate,BER)[22-23]。

對式(9)取對數(shù),然后取反得

(12)

式中,Dj(mn k)可作為當前時刻路徑量度值。

由圖3卷積編碼器的狀態(tài)圖可以得到用戶j當前時刻的路徑度量矩陣為

(13)

式中,Dj(m)是mn k取m∈{1,2,…,M}時的距離值;Inf表示狀態(tài)轉(zhuǎn)移圖中沒有這條路徑。

然后將該路徑度量矩陣送入維特比軟判決模塊,找到一條滿足最大似然函數(shù)的路徑,得到最終譯碼結(jié)果。

4 性能仿真分析

為了驗證聯(lián)合卷積編碼的SCMA系統(tǒng)的誤比特性能、收斂性等,對JDD算法進行了仿真分析。SCMA鏈路仿真信道采用了高斯信道。其中各仿真參數(shù)值為接入用戶數(shù)J=6,信道數(shù)K=4,碼本大小M=4,過載因子為150%,卷積編碼采用(2,1,2)編碼器[24]。

4.1 BER性能比較

主要針對聯(lián)合卷積編碼后的JDD算法進行仿真,重點考察聯(lián)合卷積編碼后SCMA系統(tǒng)性能提升情況。MPA中最大迭代次數(shù)設置為6次,性能仿真結(jié)果如圖6所示。為了便于比較,圖6中同時給出了原始SCMA系統(tǒng)的MPA下的曲線。

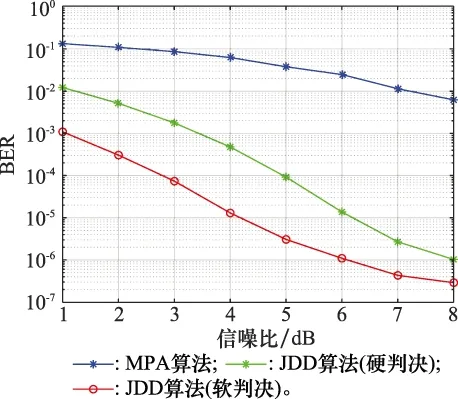
圖6 不同算法下的BERFig.6 BER of different algorithms

從圖6中可以看到,在高斯信道信噪比(signal to noise ratio,SNR)為6 dB的條件下,聯(lián)合卷積編碼的SCMA系統(tǒng),采用JDD方案后,系統(tǒng)BER從10-2左右改善到10-5以上。同時,采用軟判決的JDD方案性能要優(yōu)于采用硬判決的JDD方案。例如在BER為10-5時,兩算法有2 dB的性能差異。

4.2 迭代次數(shù)對系統(tǒng)性能影響

針對聯(lián)合卷積編碼的SCMA系統(tǒng)的最大迭代次數(shù)T分別采用1,2,4,6時,對系統(tǒng)的BER性能進行仿真(見圖7),其中算法判決方式為硬判決。

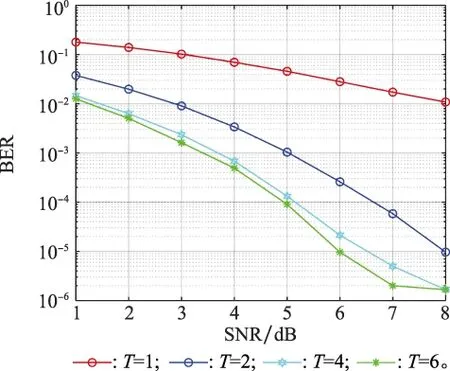
圖7 不同迭代次數(shù)下的BERFig.7 BER under different iteration times

從圖7中可以看出,在相同信道環(huán)境下,隨著算法最大迭代次數(shù)的增多,JDD方案的誤比特性能會有所提升。例如當BER為10-3時,最大迭代次數(shù)為2次時相比4次時性能損失約1.3 dB。這是因為隨著迭代次數(shù)的增多,算法會逐漸收斂,輸出判決會更加準確,算法的誤比特性能也就更好。

4.3 收斂速度分析

針對聯(lián)合卷積編碼的SCMA系統(tǒng)的誤比特性能隨迭代次數(shù)的變化進行仿真,體現(xiàn)的是算法的收斂速度,在工程實現(xiàn)中收斂速度越快,則算法整體延時越小[25]。圖8給出了當系統(tǒng)SNR為3 dB、5 dB和7 dB時,采用JDD方案的誤比特性能隨迭代次數(shù)的變化曲線。從圖8可以得出以下結(jié)論:① JDD硬判決算法在消息的迭代過程中存在著收斂點。當SNR取7 dB時,在高斯信道環(huán)境下,當?shù)螖?shù)為4時算法開始收斂。② 當算法還未收斂時,當最大迭代次數(shù)增多時,系統(tǒng)誤比特性能有所提升,但當算法趨于收斂時,JDD硬判決算法的誤比特性能不再隨著迭代次數(shù)的增加而改善這也說明了消息傳遞算法具有收斂性。

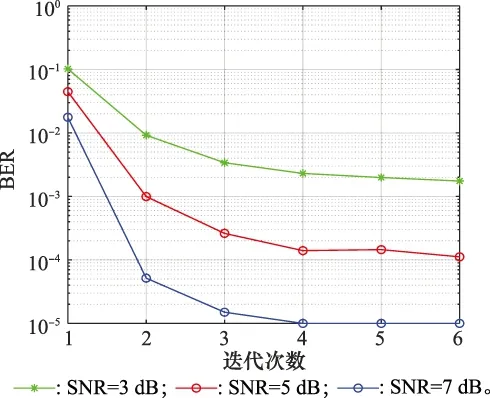
圖8 收斂性能對比Fig.8 Comparison of convergence porformance

4.4 不同算法性能分析

圖9給出了原始MPA、SD-MPA、DS-MPA以及PM-MPA聯(lián)合卷積編碼之后的誤比特性能比較,其中SD-MPA-JDD在球半徑Δ=2δ時[26]的性能跟原始MPA相差2 dB;在球半徑Δ=δ時,算法性能太差,不予考慮。PM-MPA-JDD與DS-MPA-JDD可以在降低復雜度的同時,達到與原MPA相近的誤比特性能。

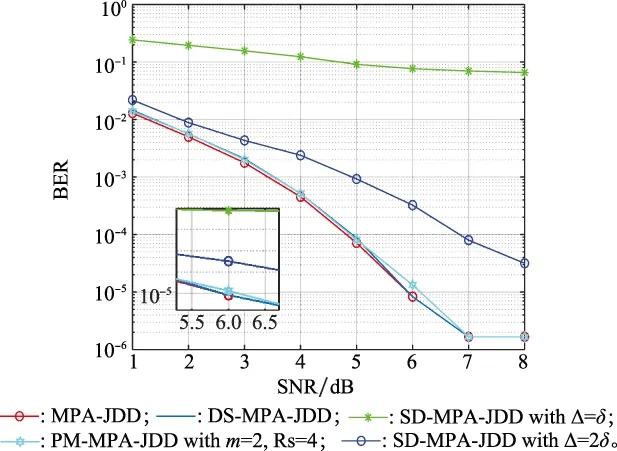
圖9 不同算法BER對比Fig.9 Comparison BER for different algorithms

原始MPA是改進算法的基礎(chǔ),這里以原始算法為例,進行算法復雜度的說明。設信道數(shù)目為K,每個信道上承載的用戶數(shù)為dr,每個用戶碼本大小為M,最大迭代次數(shù)為T。在一次迭代中,需計算K個信道中dr個用戶對M個碼字的估計概率值。那么,MPA迭代過程的計算復雜度可以表示為TKMdr。因此,乘法加法運算次數(shù)可以表示為

MUL=TKdrMd(dr-1)

(14)

ADD=TKdrM(Mdr-1-1)

(15)

同理,PM-MPA乘法加法計算量為

MUL=[mKdr+(T-m)du(J-Rs/du)]·
(Mdr-M)

(16)

ADD=[mKdr+(T-m)du(J-Rs/du)]·Mdr(dr-M)

(17)

式中,m是因子圖縮減前的迭代次數(shù);Rs是因子圖縮減后仍然參與迭代的用戶數(shù);du是每個用戶占據(jù)的信道數(shù)。

DS-MPA計算量為

MUL=(dr-1)Mdr[Kdr+(T-1)K(dr-u)]

(18)

ADD=[Kdr+(T-1)K(dr-μ)]·
(Mdr-M)+MKdr

(19)

CMP=(T-1)Kdr

(20)

圖10對各種算法的復雜度進行了比較。原始MPA的計算量是最多的。PM-MPA-JDD在整體迭代次數(shù)為2,參與整體迭代用戶數(shù)為4時,算法計算量減少了接近20%;DS-MPA-JDD在半徑Δ=2δ時減少了大約25%。

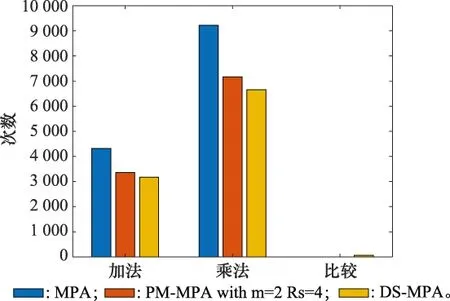
圖10 復雜度對比Fig.10 Complexity comparison

綜上所示,DS-MPA-JDD是考慮系統(tǒng)誤比特性能與算法復雜度之后,性價比較高的檢測方案。因此,DS-MPA-JDD是完全可以應用于SCMA解碼中。DS-MPA-JDD可作為本文提出的聯(lián)合卷積編碼的SCMA系統(tǒng)的最終解碼方案。

5 結(jié) 論

低軌衛(wèi)星作為目前航天領(lǐng)域和通信領(lǐng)域的研究熱點,因其覆蓋范圍廣且成本低廉,所以不論是國外還是國內(nèi)都在進行各種研究。與此同時,為保障衛(wèi)星正常運行,衛(wèi)星測控系統(tǒng)也必須同時發(fā)展。本文針對衛(wèi)星測控系統(tǒng)中用戶數(shù)量增多且BER的問題,提出一種基于SCMA和卷積編碼的聯(lián)合檢測和譯碼方案,該方案有效提升衛(wèi)星測控系統(tǒng)中系統(tǒng)容量,能滿足當前大規(guī)模衛(wèi)星測控的需求,且在譯碼過程中進行似然信息的交換,有效降低了系統(tǒng)BER。理論分析和仿真驗證了檢測算法的誤比特性能、收斂速度以及算法復雜度,并與傳統(tǒng)算法進行了比較。該算法在保證算法復雜度較低的前提下,有效提高了誤比特性能,具有簡單、易于工程實現(xiàn)等優(yōu)點。