多項分數階非線性微分方程的數值方法
喬 智,趙維加,黃健飛
(1. 揚州大學數學科學學院,江蘇揚州225002; 2. 青島大學數學與統計學院,山東青島266071)
分數階微積分[1]是數學的一個重要的分支,距今已經有300多年的歷史。近年來,分數階微積分算子的非局部性使得分數階微分方程在建模復雜動力系統和材料方面的應用越來越廣泛,比如各種黏彈性材料[2]、反常擴散[3-4]、分形理論[5]、化學和生物化學[6]。與整數階微分方程相比,分數階微分方程的物理意義更清晰,模型更簡單;但是,精確求解分數階微分方程通常比較困難。對于一些非線性分數階問題,甚至不可能獲得其精確解,因此,研究者廣泛設計和使用數值方法來求解分數階微分方程。
目前,許多論文研究了分數階常微分方程數值方法。早在1997年,Diethelm[7]對一類分數階常微分方程構造了基于求積公式的隱格式,并給出了嚴格的誤差分析。這是公認的分數階微分方程數值方法領域比較早的工作之一。隨后,Edwards等[8]研究了線性多項分數階微分方程的數值解,但是沒有考慮非線性多項分數階微分方程的情形。El-Mesiry等[9]給出了求解非線性多項分數(任意)階微分方程的數值格式,只通過數值實驗來驗證格式的計算效果。Kumar等[10]采用積分方程的思想,針對一類分數階常微分方程設計了一個高階格式,數值實驗表明該方法有較高的精度。Lin等[11]采用生成函數法推導出求解分數階常微分方程的高階近似,證明了這些方法的可解性、收斂性和穩定性,但是這些方法只能用來求解含有一個分數階導數項的方程。Ford等[12]考慮了多項分數階微分方程近似解的基于系統的分解方法,但是只考慮了各分數階指標單調遞增的情況。Huang等[13]詳細地證明了文獻[10]中所給出的數值方法至少具有3階精度。此外,關于分數階偏微分方程數值方法的研究,可以參考文獻[14-18]。
本文中研究一類多項分數階非線性常微分方程初值問題的數值方法;為了降低對解函數正則性的要求[19],利用Riemann-Liouville積分算子,將該類多項分數階非線性常微分方程化為與之等價的積分方程;為了避免求解非線性方程和保證數值方法的穩定性,分別利用復化右矩形公式和左矩形公式來離散積分方程左邊和右邊的Riemann-Liouville積分,獲得一個顯式的數值方法;分別考慮2種不同形式的多項分數階非線性微分方程,并證明2種不同問題數值方法的收斂性和穩定性。
1 情況1下數值方法的構造
考慮情況1,即0<α1<α2<…<αM<1條件下,帶有初值條件u(0)=u0的多項分數階非線性微分方程
(1)
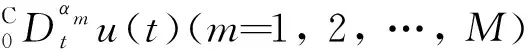
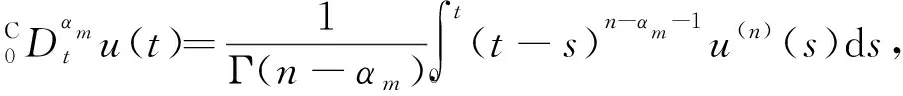
n-1≤αm≤n,
αm(m=1,2,…,M)為階數,n為正整數;u(0)為0時刻的函數值,u0為常數;f(t,u)在區間Ω上連續,其中Ω=[0,T]×,f關于第2個自變量滿足Lipschitz條件,即
|f(t,u1)-f(t,u2)|≤L|u1-u2| ,
其中Lipschitz常數L>0。
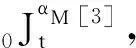
則有
(2)
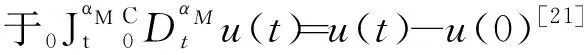
因此式(2)可化為
(3)
對于T≤1,假設f[t,u(t)]在[0,T]上一階連續,分別運用復化乘積右矩形公式和左矩形公式對式(3)左邊和右邊的Riemann-Liouville積分進行逼近,可得
(4)
成立,其中
在式(4)中,移去截斷誤差O(h),用數值解un代替精確解u(tn),則有
(5)
其中
由此,式(3)的數值方法為
(6)
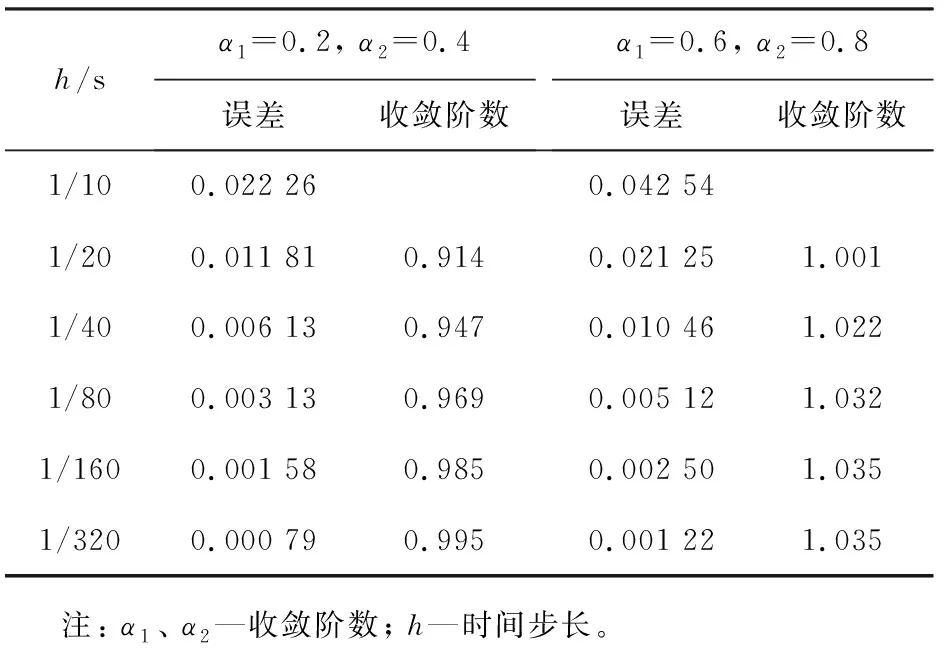
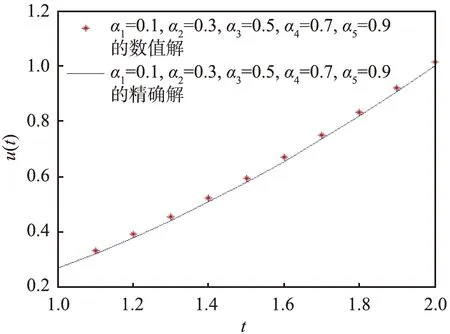
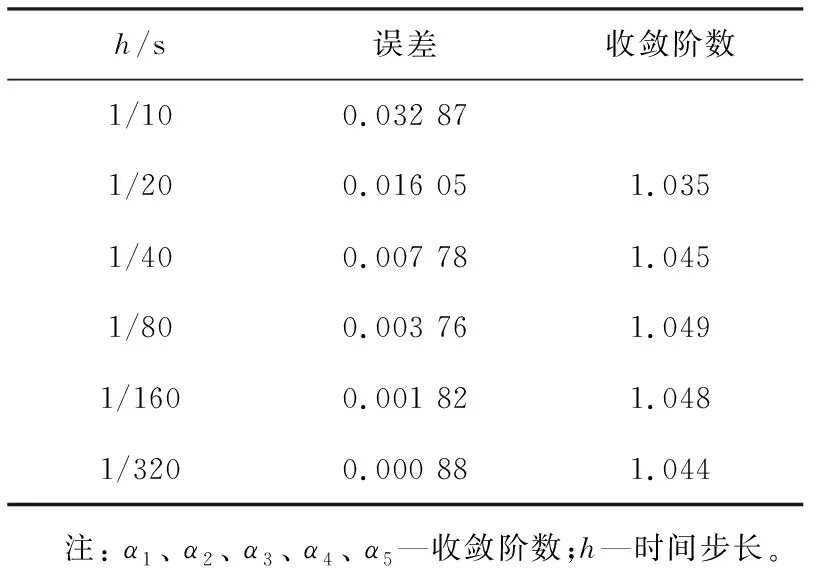
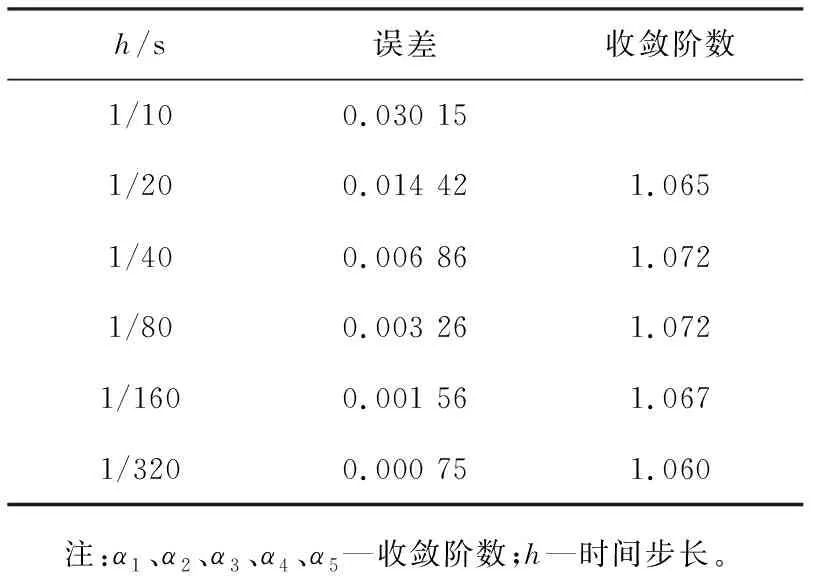
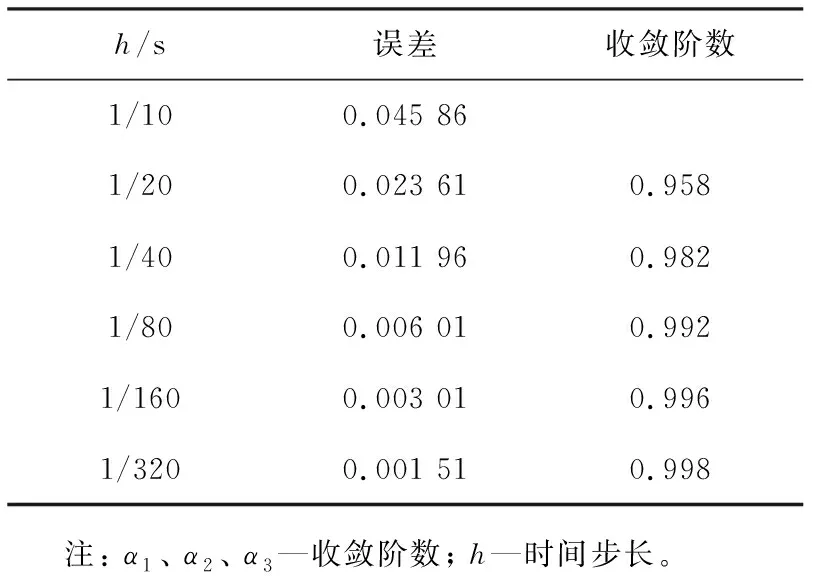
對于T≥1,對式(1)作變量替換,令sT=t,則0 (7) 與T≤1的情形相似,式(7)可離散為 (8) 在式(8)中,移去截斷誤差O(h),則數值方法變為 討論數值方法式(6)、(9)在情況1下的收斂性與穩定性。在證明過程中用到Gronwall不等式[6]。 引理1設C1>0且獨立于h>0,C2為正常數,且滿足不等式 j=0,1,…,n-1,nh≤T, 其中0<α<1,則有 |zn|≤C2Eα[C1Γ(α)Tα],nh≤T, 其中Eα為Mittag-Leffler函數,定義為 下面給出收斂性分析。 定理1假設f[t,u(t)]在區間[0,T]上一階連續,對充分小的時間步長h,式(1)的數值方法式(6)、(9)在情況1下的收斂階數為1,即|en|=|u(tn)-un|≤Ch,n=1,2,…,N,其中C為與離散化參數無關的常數,并且C可能有不同的值。 證明: 由于式(6)、(9)的收斂性分析類似,因此只證明式(6)的收斂性。f[t,u(t)]在區間[0,T]上一階連續,根據中值定理,存在Lk,使得 f[tk,u(tk)]-f(tk,uk)=Lk[u(tk)-uk]=Lkek, k=1,2,…,N。 成立,其中ek=u(tk)-uk。f(t,u)滿足Lipschitz條件,則|Lk|≤L。對于0<β<1,1≤k≤n-1,有 (10) 和 (11) 式(10)減式(11),并進行簡單放縮,有 由于tn-k=h(n-k),因此 ChαM-α1|en|+Ch。 考慮到tn-k∈ (0,1],有 CMhαM-αM-1|en|+Ch≤ CMhαM-αM-1|en|+Ch, 因此 (1-CMhαM-αM-1)|en|≤ 當h充分小時,由引理1,可得 定理1證畢。 利用定理1的證明思想,可以建立數值方法式(6)、(9)的穩定性結果。 定理2對于充分小的h,式(1)的數值方法式(6)、(9)是無條件穩定的,即 由于穩定性分析與收斂性分析類似,因此定理2證明略。 考慮式(1),初值條件為u(0)=u0,u′(0)=a且0<α1<α2<…<αM-1<1<αM<2,αM-αM-1>1。應用情況1中的離散化方法,可以得到 由此可知,在情況2條件下的數值方法為 (12) 下面給出數值方法式(12)的收斂性和穩定性分析。 定理3在式(1)中,假設f[t,u(t)]在區間[0,T]上一階連續,且對充分小的h,在情況2下,數值方法式(12)的收斂階數為1,即 |en|=|u(tn)-un|≤Ch,n=1,2,…,N。 證明: 與情況1相似,有 由于αM-αM-1-1>0,…,αM-α1-1>0,因此 對于充分小的h,根據Gronwall不等式,有 |en|≤Ch。 定理3證畢。 定理4對于充分小的h,求解式(1)的數值方法式(10)是無條件穩定的,即 證明: 與情況1的穩定性分析相似,等式 由于αM-αM -1-1>0,…,αM-α1-1>0,因此 對于充分小的h,根據Gronwall不等式,有 |εn|≤Cη。 定理4證畢。 例1分別在T=1 s和T=2 s時考慮初值條件為u(0)=0的帶有2項Caputo導數的方程 其中0<α1<α2<1。該方程的精確解為u(t)=tα2+1。注意到方程右端的光滑性滿足定理1的條件。圖1所示為T=1 s且h=0.025 s時,精確解和數值解的比較。從圖中可以看出,數值解與精確解非常一致。表1所示為當T=1 s,α1=0.1,α2=0.3,α1=0.8,α2=0.9且不同時間步長時式(6)的誤差和收斂階。表2所示為當T=2 s,α1=0.2,α2=0.4,α1=0.6,α2=0.8且不同時間步長時式(9)的誤差和收斂階。從表1、2中可以看出,隨著步長h的減小,數值方法的誤差也減小,收斂階約數為1。 α1、α2—收斂階數; t—時間; u(t)—關于t的函數。圖1 時間T=1 s, α1=0.1,α2=0.3,α1=0.8, α2=0.9時方程的數值解與精確解 表1 時間T=1 s, α1=0.1, α2=0.3,α1=0.8, α2=0.9且不同時間步長時式(6)的誤差和收斂階數 表2 時間T=2 s,α1=0.2,α2=0.4,α1=0.6,α2=0.8且不同時間步長時式(9)的誤差和收斂階數 例2分別在T=1 s和T=2 s時,考慮初值條件為u(0)=0的帶有5項Caputo導數的方程 其中0<α1<α2<α3<α4<α5<1。該方程的精確解為u(t)=tα5+1。圖2所示為當T=2 s,h=0.05 s,α1=0.1,α2=0.3,α3=0.5,α4=0.7,α5=0.9時方程的精確解和數值解。從圖中可以看出,數值解與精確解非常吻合。表3所示為T=1 s,α1=0.1,α2=0.3,α3=0.4,α4=0.8,α5=0.9且不同步長時式(6)的誤差和收斂階數。表4所示為T=2 s,α1=0.1,α2=0.3,α3=0.5,α4=0.7,α5=0.9且不同步長時式(9)的誤差和收斂階數。從表3、4中可以看出,當h減小到之前的1/2時,誤差也減小到之前的1/2,收斂階約數為1。 α1、α2、α3、α4、α5—收斂階數; t—時間; u(t)—關于t的函數。圖2 時間T=2 s,α1=0.1,α2=0.3,α3=0.5,α4=0.7,α5=0.9時方程的數值解與精確解 表3 時間T=1 s,α1=0.1,α2=0.3,α3=0.4,α4=0.8,α5=0.9且不同時間步長時式(6)的誤差和收斂階數 表4 時間T=2 s,α1=0.1,α2=0.3,α3=0.5,α4=0.7,α5=0.9且不同時間步長時式(9)的誤差和收斂階數 例3 當T=2 s時,考慮初值條件為u(0)=0,u′(0)=0的帶有3項Caputo導數的方程 其中0<α1<α2<1<α3<2。該問題的精確解為u(t)=tα1+2。表5所示為當T=2 s,α1=0.3,α2=0.7 ,α3=1.5時式(12)的誤差和收斂階數。從表中可以看出,當h減小時,誤差也隨之減小,并且收斂階數趨近于1。 表5 時間T=2 s,α1=0.3,α2=0.7,α3=1.5且不同步長時式(10)的誤差和收斂階數 本文中基于等價的積分方程,對具有不同初值條件的多項分數階非線性微分方程,構造了具有一階精度的顯式數值方法。針對2個不同的初值問題,證明了數值方法的收斂性和穩定性。最后,通過計算帶有2、5、3項Caputo分數階導數的數值算例,驗證了理論分析結果的正確性。在以后的研究中,將嘗試把本文中的數值方法擴展到多項時間分數階偏微分方程的數值求解。2 情況1下數值方法的收斂性與穩定性
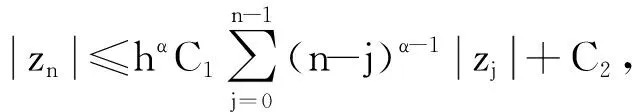
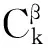

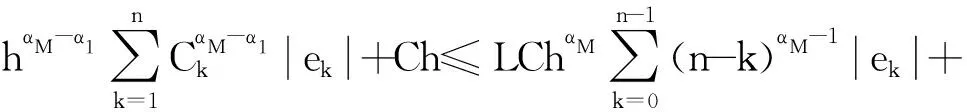
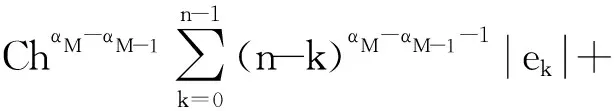
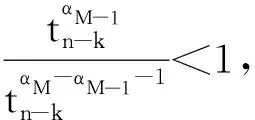
3 情況2下數值方法的構造以及收斂性與穩定性
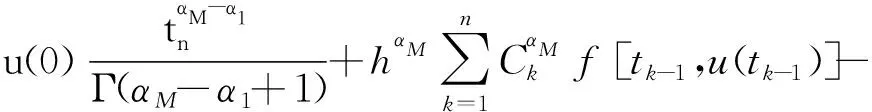
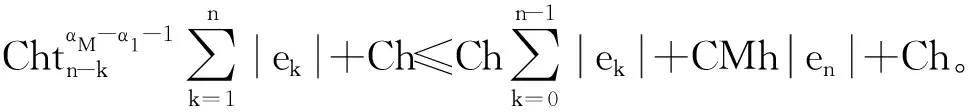
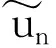

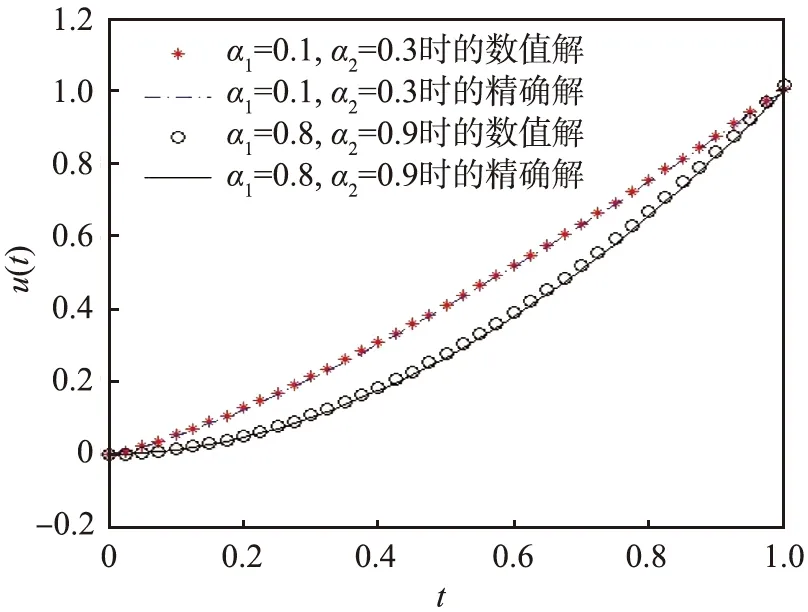
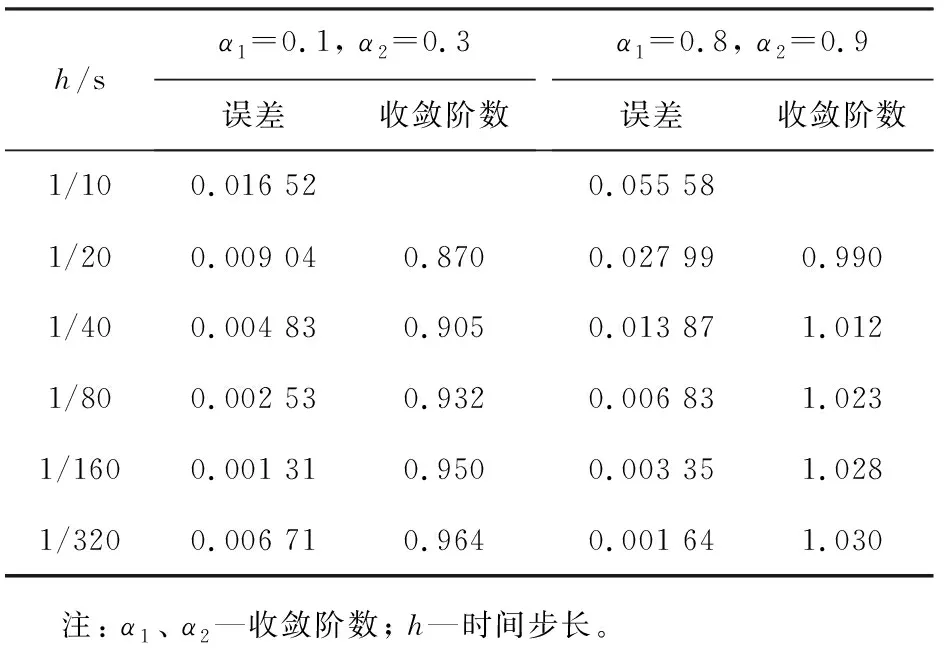
4 數值實驗
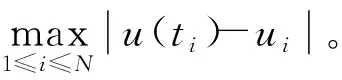
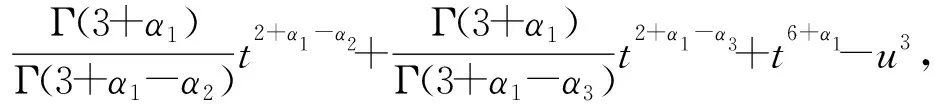
5 結論

