基于迭代學習控制的劃片機高精度運動誤差補償
王建新,鄭 浩
(1.沈陽工業大學人工智能學院,沈陽110870;2.沈陽儀表科學研究院有限公司,沈陽110043)
1 引 言
劃片機作為電子元器件封裝的關鍵設備,其系統穩定性、可靠性和加工精度對劃切質量起到關鍵的作用。然而因種種現實因素的存在,在劃片機加工過程中會產生許多不同種類的誤差,比如在系統運動過程中由溫度而造成的熱變形誤差、劃片機床自身幾何誤差、動力學誤差等等。這就對劃片機的高精度運動誤差補償提出了更高要求。傳統的誤差補償方法主要是采用機理建模或者辨識建模,擬合出一條離線線性曲線,但此法可能會造成較大的擬合誤差,可實現性差。在此問題上,隨后出現了采用數據驅動[1]中迭代學習控制的方法,來實現劃片機運動誤差補償。
1984 年,日本學者有本卓[2]首次提出了迭代學習算法,之后便得到廣泛應用。由于迭代學習控制算法無須建立精確的被控對象物理模型,僅僅通過輸入輸出數據就可完成控制系統的設計,解決了模型建模困難的問題。張潔潔[3]采用基于數據驅動的無模型自適應迭代誤差補償方法嘗試解決傳統問題的難點,雖然誤差補償的精度有所提升,但是隨著迭代次數的增加無法保證系統收斂。孟婷婷[4]通過設計迭代學習控制器提高了系統的收斂性,但只能解決單軸的跟蹤誤差,無法達到多軸的運動控制誤差補償。梁建智[5]通過迭代學習算法將數控機床加工動力學過程轉化為迭代數據模型,有效提升了加工精度。
2 迭代學習控制原理及神經網絡
2.1 迭代學習控制
在處理系統運動控制任務時,往往要通過被控對象的實際運行軌跡與期望軌跡之間的差值進行調整,迭代學習正是利用這一原理,依靠前一次或前幾次操作測得的誤差信息來修正控制輸入,通過不斷重復,使得該重復任務在下一次操作時更加準確,最終達到整個時間區間上輸出軌跡與期望軌跡的重合。
迭代學習控制[6]通過函數迭代方法來實現,即構造用于修正控制的學習律,使得它產生一個函數序列{uk(t)},收斂于u(t)。迭代學習律的典型形式為:

其中k=1,2,...N,代表周期數;uk+1(t)代表第k+1 次操作時的操作輸入;uk(t)表示當前操作使用的輸入,ek(t)=yd(t)-yp(t),表示當前操作誤差;U(uk(t),t)表示當前所得到的誤差學習方式。學習律常用表現形式有如下兩種:
D 型學習律:
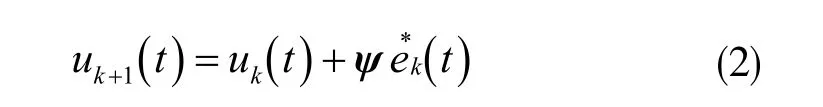
P 型學習律:

其中, ek(t)表示誤差,φ 表示定常增益矩陣。
為保證系統訓練的穩定性,迭代學習具有相同的初始狀態,常見的初始條件有:
①迭代初態與期望初態一致,即xk(0)=xd(0)(,k=1,2,...),稱作初始狀態嚴格重復;
②迭代初始狀態固定;
2.2 神經網絡
神經網絡是由多個神經元按照一定規則連接起來所構成,主要包括輸入層、隱藏層、輸出層,結構圖如圖1 所示。其中,輸入層負責接收輸入數據;輸出層負責獲取神經網絡輸出數據;隱藏層位于輸入層和輸出層之間,外部不可見。神經網絡的結構類型有很多,比如:卷積神經網絡、循環神經網絡等。此處選用BP(Back Propagation)神經網絡結構。

圖1 神經網絡結構圖
3 系統設計
3.1 劃片機系統結構
本設計中劃片機系統的控制器采用三環控制結構,分別為電流環、速度環、位置環。三環控制結構框圖如圖2 所示[7]。I(s)、V(s)、P(s)分別表示電流環控制器、速度環控制器、位置環控制器。E(s)、M(s)分別代表電力系統和機械系統。
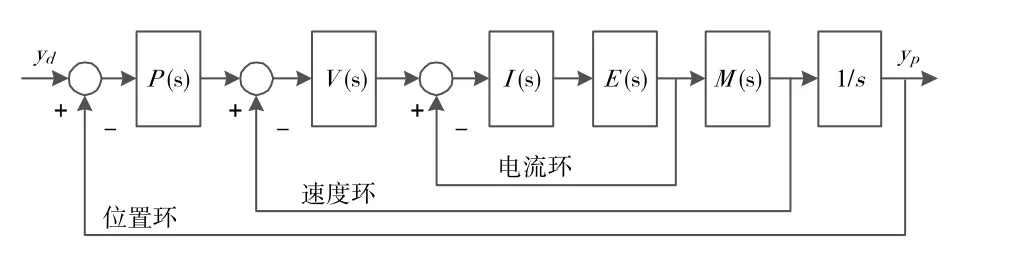
圖2 劃片機系統三環結構圖
此處所采用的迭代學習控制算法不需要建立精確模型,僅需系統運動過程中產生的輸入輸出數據不斷迭代即可達到誤差補償,所以僅僅需要位置環,將速度環和電流環以及被控對象整體封裝成一個新的被控對象。通過對位置環參數的調整,形成一個新的控制系統。
3.2 劃片機迭代控制系統設計
劃片機運動控制系統[8]采用迭代學習控制算法的目標是能夠精確地跟蹤參考軌跡從而達到高精度定位。跟蹤誤差ep(k)=yd(k)-yp(k)盡可能接近0(其中yd(k)表示期望軌跡,yp(k)表示實際軌跡)。此處的算法是通過系統輸入輸出數據實現的,所以設計一個誤差補償環路,不需要對誤差進行建模,從系統的輸出位置得到實際的運行軌跡。誤差補償[9]迭代控制過程如圖3 所示。控制律結構如圖4 所示。
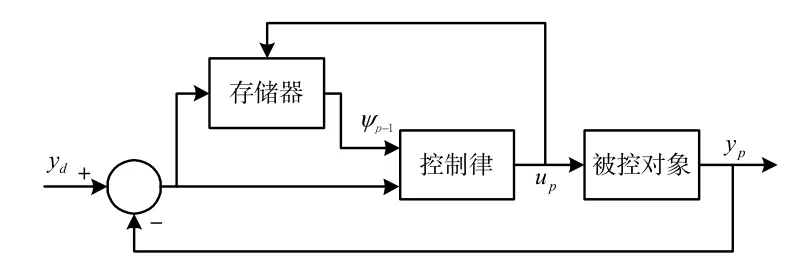
圖3 誤差補償迭代控制框圖
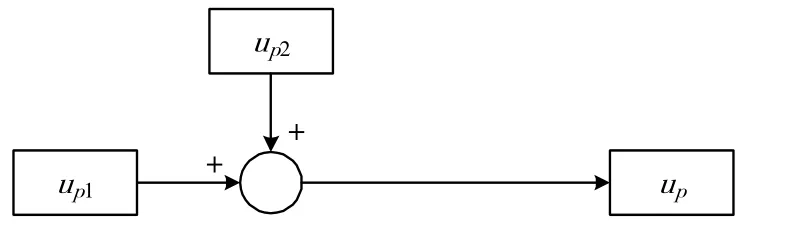
圖4 控制律結構框圖
圖4 中,up(k)=up1(k)+up2(k)。其中up1(k)表示迭代學習控制器,它的表現形式為:
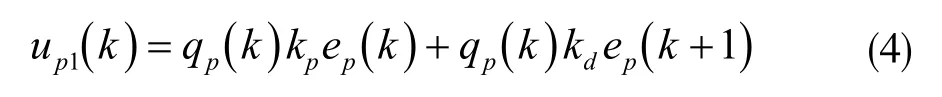
式中,qp(k)∈{0,1},當qp(k)=0 表示數據缺失;qp(k)=1則表示沒有缺失。kp為比例因子,kd表示微分因子。當kd=0,為P 型控制律;當kp=0,為D 型控制律;當kp≠0 且kd≠0,則為PD 型控制律。
up2(k)為迭代神經網絡控制器,它的表現形式為:
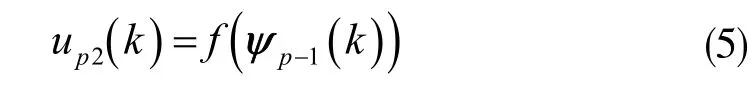
式中,f 表示非線性函數;ψp-1(k)表示p-1 時刻的向量,它的形式決定著控制器的結構,規則如下:
P 型控制律:

D 型控制律:
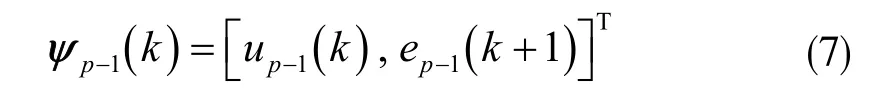
PD 型控制律:
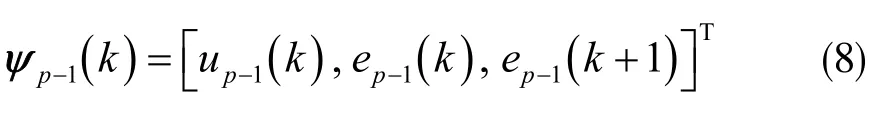
控制系統的目的是經過多次重復試驗找到一個非線性函數f,實現盡可能最小的軌跡誤差[10]。為降低建模誤差對參數優化過程的影響,同時提高算法的跟蹤性能,在此選擇傳統PD 型控制律與神經網絡結合設計PD 神經網絡迭代控制器。神經網絡有很好的泛化性,能夠提高系統的控制性能。采用的神經網絡為全連接層,形式為:
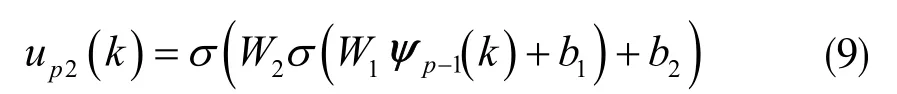
式中,W1、W2、b1、b2分別為輸入層到隱藏層、隱藏層到輸出層的權重和偏差。σ 為隱藏層和輸出層的激活函數。公式(9)主要依賴迭代控制器Ψp-1(k)向量以前的重復實驗所決定。
4 仿真結果與分析
為驗證劃片機迭代控制系統有效性,給定劃片機運動控制系統跟蹤期望軌跡為yd(t)=sin(t)。劃片機位置伺服系統采樣步長為0.01,仿真時間為10 s,迭代次數為30 次。
首先對簡單的P 型控制律迭代控制進行仿真分析,仿真結果如圖5 所示。
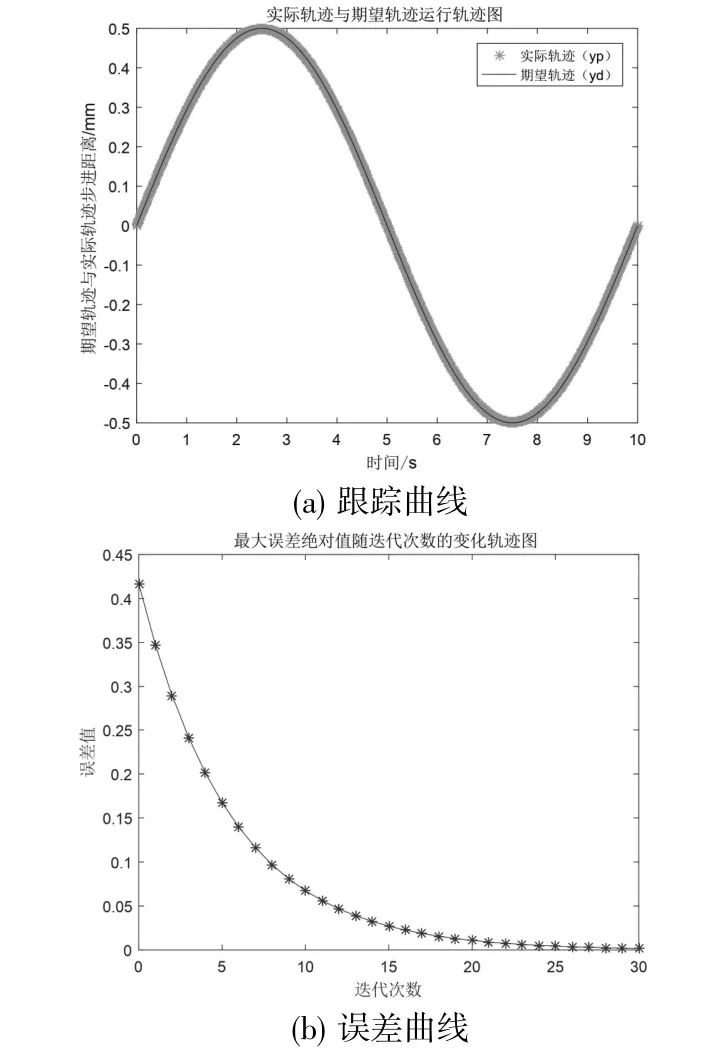
圖5 P 型控制律迭代控制仿真結果
由圖5(a)可見,隨著迭代次數的增加,實際軌跡逐漸逼近期望軌跡;從圖5(b)可以看出隨著運行次數的增加,系統的跟蹤誤差越來越小,并趨于穩定。
然后對PD 型控制律迭代控制進行仿真分析,結果如圖6 所示。
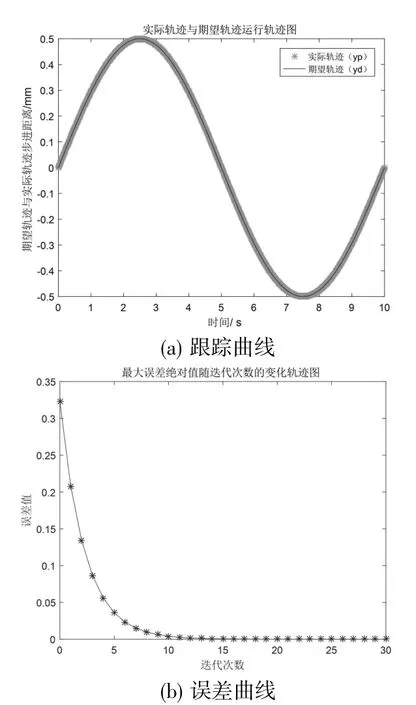
圖6 PD 型控制律迭代控制仿真結果
從圖6(a)中可看出,隨著迭代次數增加,實際軌跡已經跟蹤上期望軌跡,但是收斂速度不夠快;從圖6(b)可見控制系統運動的跟蹤誤差已經很小了。
最后對迭代神經網絡控制律進行仿真分析,仿真結果如圖7 所示。從圖7(a)可以看出實際軌跡很好地跟蹤上了期望軌跡;從圖7(b)可見,跟蹤誤差隨著迭代次數增加逐漸變小,并且收斂速度變快。
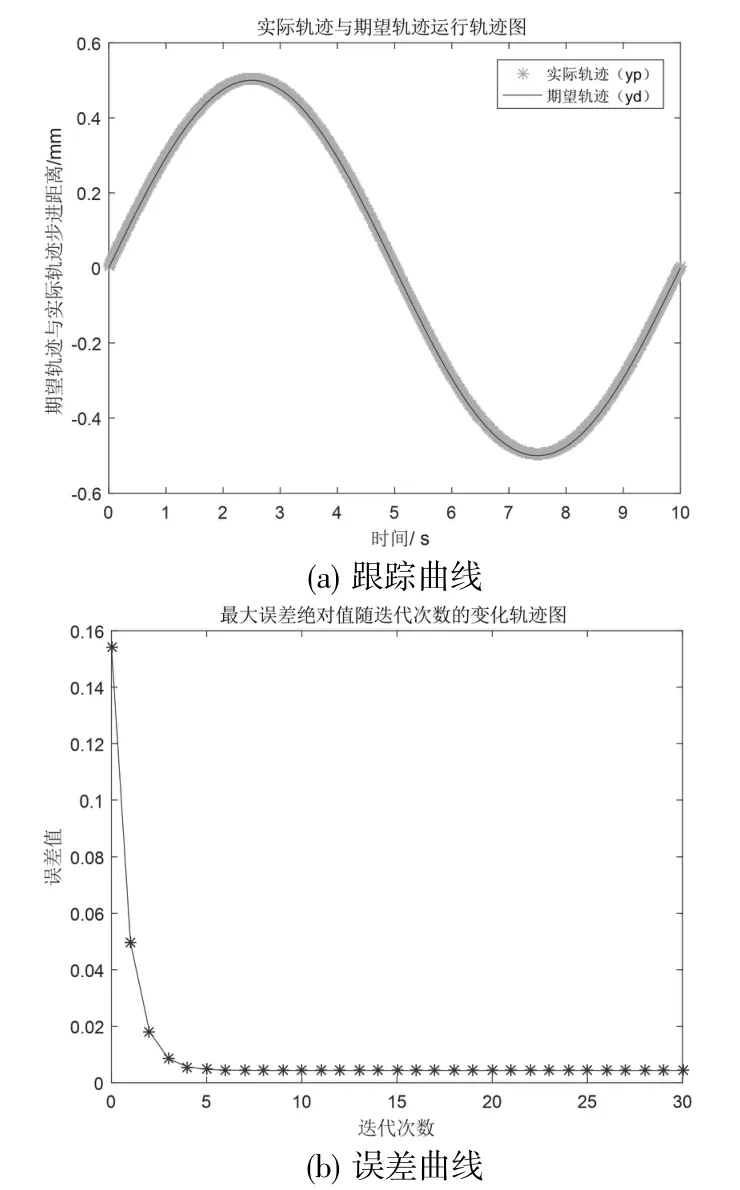
圖7 神經網絡控制律迭代控制仿真結果
從仿真結果可見,隨著迭代次數的變化,在跟蹤誤差方面,迭代學習神經網絡控制方法明顯優于P型、PD 型迭代學習控制法。此外,迭代學習控制神經網絡的權重和偏差增益是迭代式變化,而P 型和PD 型迭代學習控制的控制增益是固定不變的,就決定了迭代學習控制神經網絡每次迭代能尋找到更優化的控制,具有更快的收斂性,控制精度也得到提高,有效實現了劃片機運動軸的誤差補償。
5 結 束 語
在對劃片機運動控制伺服系統分析的基礎之上,利用迭代學習神經網絡算法完成了劃片機誤差補償控制系統的設計。分別對于P 型、PD 型控制律以及神經網絡迭代控制進行仿真分析,驗證了采用迭代學習控制神經網絡方法能夠有效的提高控制精度,該設計對系統的各軸運動控制都具有同樣適用性,在實際使用中能夠有效提高工作效率。

