船身式水陸兩棲飛機(jī)起降飛行仿真研究

王崢華，段旭鵬，程志航，孫衛(wèi)平

(中航通飛研究院有限公司 總體部， 珠海 519040)

0 引 言

水陸兩棲飛機(jī)可以利用船身在水面上起飛著水，在陸上機(jī)場使用專門設(shè)計(jì)的起落架完成地面起降。日本和俄羅斯等國發(fā)展了US-1、US-2、Be-200等成熟的大型水陸兩棲飛機(jī)，在該類型飛機(jī)地面、水面操縱特性的適航驗(yàn)證方面建立了完整的技術(shù)體系、積累了豐富的設(shè)計(jì)經(jīng)驗(yàn)。我國在建立水陸兩棲飛機(jī)起降數(shù)學(xué)模型并應(yīng)用到型號方案優(yōu)化設(shè)計(jì)、地面和水面適航條款適航符合性計(jì)算評估等方面的研究尚不完善，與國外存在著一定的差距。以往開展地面和水面操縱特性的適航符合性驗(yàn)證工作直到研發(fā)試飛階段才能開展，如果試飛結(jié)果表明不滿足適航條款要求，再嘗試修改不同的設(shè)計(jì)方案以滿足適航要求，這會付出巨大的時(shí)間代價(jià)和經(jīng)濟(jì)成本。此外，飛機(jī)起降階段的時(shí)間占總飛行時(shí)間的6%，事故率卻占到了80%以上，可見起降階段的飛行安全性研究不容忽視，建立較高精度的水陸兩棲飛機(jī)不同介質(zhì)起降的數(shù)學(xué)模型具有重要意義。

水陸兩棲飛機(jī)水動力的數(shù)學(xué)建模方面，遠(yuǎn)不及氣動力模型研究得深入和成熟，目前針對船體水動力數(shù)學(xué)建模的方法通常為近似計(jì)算公式，主要有：①Savitsky半理論半經(jīng)驗(yàn)水動力計(jì)算方法。D.Savitsky基于滑行平面假設(shè)提出了水動力、水動力矩的計(jì)算方程，并對側(cè)舷浸濕面積、噴濺浸濕面積、噴濺阻力等進(jìn)行了逐步改進(jìn)，提高了該方法計(jì)算水作用力的估算精度。②ЦАГИ法。ЦАГИ法與Savitsky方法的區(qū)別在于采用了不同的浸濕面積修正方法。蘇聯(lián)中央空氣動力學(xué)與水動力學(xué)研究院采用平板假設(shè)計(jì)算浸濕面積、升力、縱傾角，提出了棱形艇升力和力矩方程，該方法對滑行艇起滑階段水動力計(jì)算精度較高；董文才等提出了一種ЦАГИ法結(jié)合RANS方程的計(jì)算方法進(jìn)一步提高了水阻力計(jì)算精度。③二維切片理論方法。近似將船體水線以下水流變化等效成無數(shù)個(gè)二維楔形面沖擊水面過程中產(chǎn)生的水流運(yùn)動，作用在船體的總水作用力等于所有二維平面流體作用力的總和。J.A.Keuning使用該方法建立了不規(guī)則波浪上滑行艇六自由度非線性數(shù)學(xué)模型；K.Grame進(jìn)一步改進(jìn)該方法，在模型中增加相關(guān)修正算子以提高數(shù)學(xué)模型對俯仰角運(yùn)動的計(jì)算精度；朱迎谷等基于二維切片理論和Savitsky水動力計(jì)算方法開展了船身型水上無人機(jī)起飛過程的縱向非線性數(shù)學(xué)建模和自動控制律設(shè)計(jì)研究；段旭鵬等針對水上飛機(jī)復(fù)雜外形船體，利用計(jì)算流體力學(xué)技術(shù)對船體切片數(shù)值積分的方法，分析了水面起飛滑行過程中的水動力特性。

水陸兩棲飛機(jī)的起落架不同于常規(guī)陸基飛機(jī)，主起落架需在水面運(yùn)行時(shí)收于水線之上，造成了起落架結(jié)構(gòu)高度遠(yuǎn)高于一般陸基飛機(jī)；大長寬比的船身又使得起落架主輪距較小。飛機(jī)地面運(yùn)行時(shí)由機(jī)體、起落架支柱、機(jī)輪以及道面等多個(gè)剛體和柔性體組成了多體系統(tǒng)。國外, R.George等、D.H.Klyde等、W.S.Pi等分別對起落架地面運(yùn)動進(jìn)行建模和仿真，并已應(yīng)用于起落架工程設(shè)計(jì)優(yōu)化、地面操縱特性分析之中。國內(nèi)，張明等建立了綜合飛機(jī)本體、前輪轉(zhuǎn)彎、防滑剎車的地面運(yùn)動數(shù)學(xué)模型，仿真研究了地面勻速轉(zhuǎn)彎和滑跑剎車的動態(tài)響應(yīng)；詹家禮和韓紀(jì)軍等分別在ADAMS、LMS Virtual Lab軟件中建立了水陸兩棲飛機(jī)的起落架系統(tǒng)結(jié)構(gòu)動力學(xué)仿真模型，進(jìn)行了地面滑跑仿真分析；劉海良等利用建立的地面運(yùn)動數(shù)學(xué)模型，通過人機(jī)閉環(huán)數(shù)字飛行仿真評估了民用飛機(jī)地面操縱特性的適航符合性。

在上述研究成果的基礎(chǔ)上，本文從某大型水陸兩棲飛機(jī)適航符合性分析、水面控制律設(shè)計(jì)等工程應(yīng)用的實(shí)際需求出發(fā)，利用與上述研究不同的建模方法，分別建立該型飛機(jī)的水動力數(shù)學(xué)模型和起落架數(shù)學(xué)模型；聯(lián)立飛機(jī)本體六自由度飛行力學(xué)模型分別開展水面、陸地的起降飛行仿真，并利用仿真計(jì)算得到的飛機(jī)運(yùn)動參數(shù)與水池試驗(yàn)、飛行試驗(yàn)結(jié)果進(jìn)行對比分析。

1 水動力模型

基于某大型水陸兩棲飛機(jī)水池試驗(yàn)測量的水動阻力、水動升力、浮力等水動力分量(如圖1 所示)，建立靜水滑行中的縱向水動力數(shù)學(xué)模型。浮力和浮心的計(jì)算方法主要基于阿基米德定律，文中不再列出其具體公式。

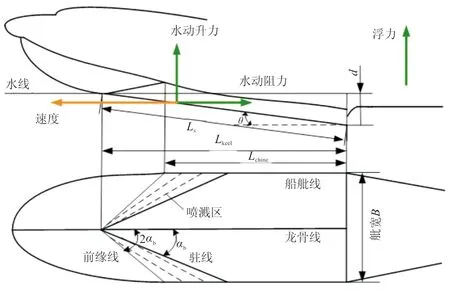
圖1 船體水面運(yùn)動的關(guān)鍵參數(shù)和受力

1.1 水動升力

水動升力與氣動升力產(chǎn)生機(jī)理相似，均與動壓、浸潤面積和升力系數(shù)相關(guān)。水陸兩棲飛機(jī)船體水動升力的計(jì)算表達(dá)式為

(1)

式中：

ρ

為水的密度；

V

為飛機(jī)速度；

S

為浸濕面積，

S

=

λB

；

B

為舭寬；

C

w為水動升力系數(shù)；

θ

為縱傾角；

λ

為浸濕長寬比。

(2)

式中：

L

為船身平均浸濕長度；

L

為龍骨浸濕長度；

L

為船舭線浸濕長度；

d

為斷階下緣點(diǎn)在水線以下的垂直距離；

β

為船體斜升角。

1.2 水動阻力

本文所建立的水動阻力

D

模型為

(3)

式中：

D

為黏性阻力；

D

為噴濺阻力；(1+

k

)為形狀因子，僅與船體形狀有關(guān)，參考與兩棲飛機(jī)船體相似的船模試驗(yàn)結(jié)果，

k

修正為0.195。船體底部平均水流速度

V

小于飛機(jī)的前進(jìn)速度

V

，與機(jī)身底部的平均動壓

P

有關(guān)，根據(jù)伯努利方程可得：

(4)

噴濺區(qū)面積

A

：

(5)

噴濺阻力系數(shù)

C

：

(6)

式中：

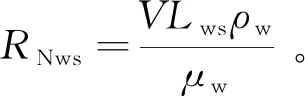
L

為噴濺特征長度；

μ

為水的黏性系數(shù)，

μ

=0.001 002 kg/(m·s)。

1.3 水動作用點(diǎn)

水陸兩棲飛機(jī)在水面滑行時(shí)船體底部的水動壓力分布如圖2所示，70%左右的水動壓力分布在滑行面與水面相遇的部位，本文參考蘇聯(lián)中央空氣動力學(xué)與水動力學(xué)研究院的相關(guān)研究成果，其水動壓力中心的計(jì)算公式為

(7)

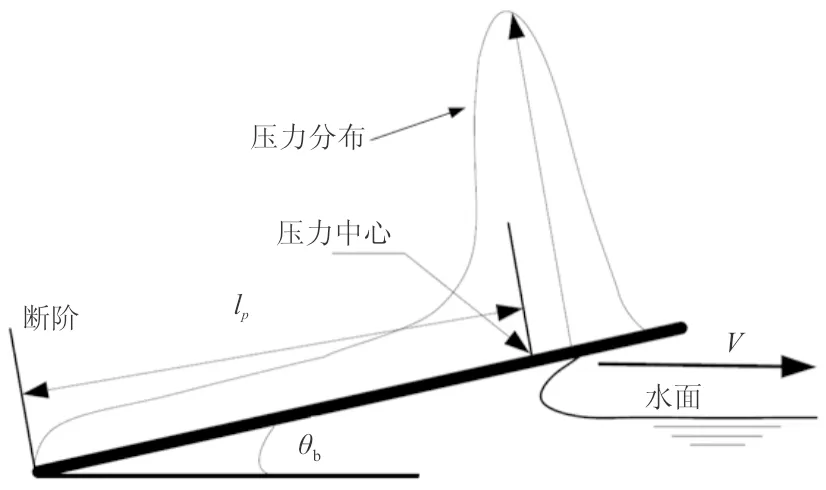
圖2 船體底部的水動壓力分布

2 起落架模型

在某大型水陸兩棲飛機(jī)支柱式起落架建模的過程中，將機(jī)輪、起落架支柱、緩沖器活塞等非彈性支撐質(zhì)量的參考點(diǎn)定位于機(jī)輪軸心處，具有3個(gè)方向的平動自由度，機(jī)輪繞輪軸具有1個(gè)轉(zhuǎn)動自由度。起落架緩沖器沿軸向具有1個(gè)平動自由度，同時(shí)可沿航向和側(cè)向發(fā)生彎曲變形，但不考慮支柱扭轉(zhuǎn)變形。機(jī)體等彈性支撐質(zhì)量為具有3個(gè)方向的平動和3個(gè)轉(zhuǎn)動自由度的剛體，其參考點(diǎn)位于飛機(jī)的重心處。

(a) 第k個(gè)起落架的支柱

(b1) 側(cè)視圖

(b2) 俯視圖

第

k

個(gè)起落架支柱在機(jī)輪軸線參考點(diǎn)

W

處作用于機(jī)輪的力為

(8)

3 仿真模型

根據(jù)上述水動力模型、起落架模型，結(jié)合飛機(jī)本體飛行力學(xué)仿真模型(包含由風(fēng)洞試驗(yàn)數(shù)據(jù)建立的氣動力模型、發(fā)動機(jī)拉力特性模型等)，利用MATLAB/Simulink所建立的仿真軟件(如圖4 所示)，可以分別實(shí)現(xiàn)地面和水面起降階段的實(shí)際飛行任務(wù)仿真。

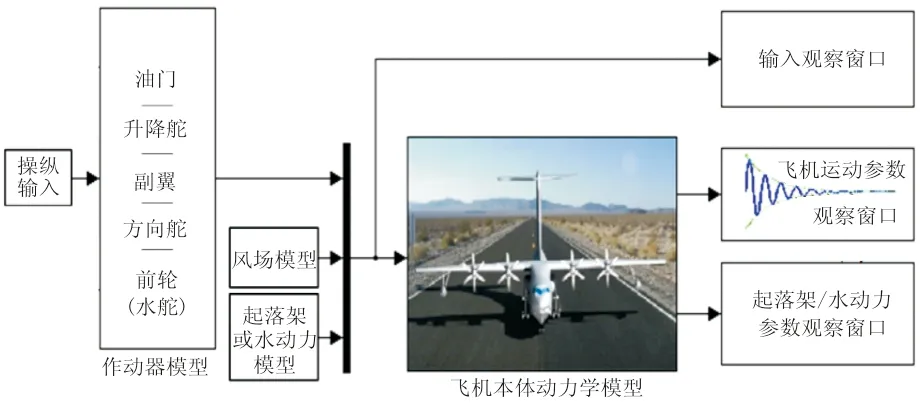
圖4 飛行仿真的結(jié)構(gòu)框圖

4 仿真算例

4.1 水面起飛

本算例計(jì)算某大型水陸兩棲飛機(jī)以給定起飛構(gòu)型(質(zhì)量53 500 kg、重心26%

MAC

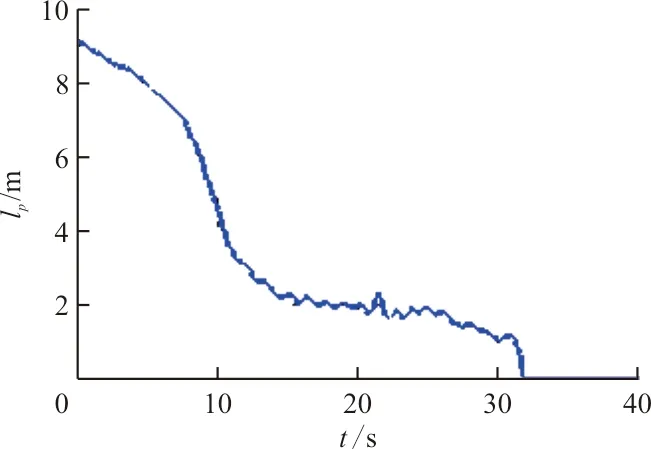
、襟翼20°)從平靜水面以速度1.5 m/s、起飛功率起飛的過程，升降舵舵面預(yù)置在水池試驗(yàn)偏度-15°。初始配平計(jì)算的俯仰角為2.74°，與水池試驗(yàn)得到的初始浮態(tài)2.75°基本相同。

水陸兩棲飛機(jī)水面起飛過程仿真結(jié)果如圖5所示，“計(jì)算值”為利用水動力數(shù)學(xué)模型進(jìn)行飛機(jī)飛行仿真的結(jié)果，“試驗(yàn)值”為飛機(jī)在相同狀態(tài)下的水池試驗(yàn)值，其中水動阻力和水動升力的試驗(yàn)值是基于水池縮比模型試驗(yàn)數(shù)據(jù)換算為實(shí)機(jī)尺寸后的結(jié)果。

(a) 縱傾角

(b) 高度

(c) 速度

(d) 水動阻力

(e) 水動升力

(f) 水動作用點(diǎn)

從圖5可以看出：飛機(jī)在12 s時(shí)達(dá)到縱傾峰，峰值約為6.2°，31 s時(shí)飛機(jī)離水；水面滑行過程中俯仰角處于水池試驗(yàn)穩(wěn)定邊界之內(nèi)，不會出現(xiàn)不穩(wěn)定運(yùn)動，符合適航規(guī)范的要求；質(zhì)心高度和速度的變化規(guī)律與試驗(yàn)值相同；水動阻力的峰值與試驗(yàn)值誤差為8.7%；水動力作用點(diǎn)在起飛過程中逐漸向船體斷階移動，也符合理論規(guī)律。

4.2 地面起飛

利用建立的地面仿真模型，計(jì)算大型水陸兩棲飛機(jī)在某次給定起飛構(gòu)型(質(zhì)量48 000 kg、重心25.5%

MAC

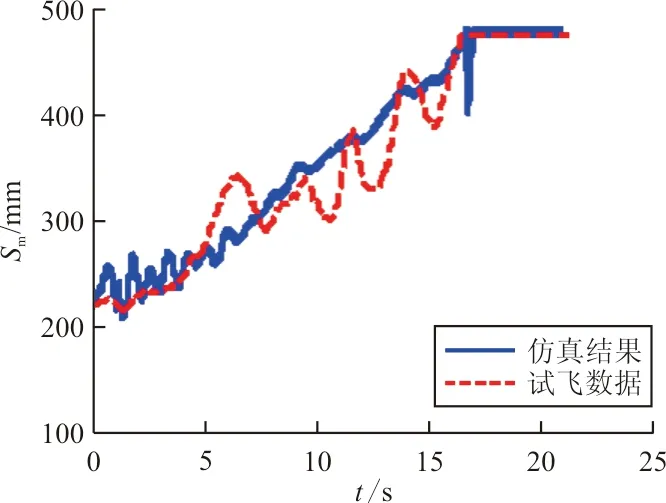
、襟翼20°、起飛功率)從速度5 m/s開始滑跑起飛的過程，舵面輸入與飛行員操縱時(shí)間歷程相同。初始配平狀態(tài)為俯仰角0.3°、質(zhì)心高度4.37 m。水陸兩棲飛機(jī)地面起飛過程仿真結(jié)果如圖6所示。

(a) 高度

(b) 速度

(c) 升降舵

(d) 俯仰角

(e) 前輪緩沖器行程

(f) 主輪緩沖器行程

從圖6可以看出：在滑跑、拉桿、離地起飛過程中，飛機(jī)的速度、高度、俯仰角等關(guān)鍵運(yùn)動參數(shù)與試飛數(shù)據(jù)吻合較好；在未拉桿之前隨著速度增加，全機(jī)升力增大使飛機(jī)呈現(xiàn)低頭趨勢，該現(xiàn)象符合一般起飛過程的俯仰角變化趨勢，飛機(jī)沒有前翻傾向能夠滿足適航條款的要求；仿真計(jì)算的前主輪緩沖器的行程變化初始滑跑段有一定誤差，但也基本落在試飛數(shù)據(jù)振蕩曲線之內(nèi)。

5 結(jié) 論

(1) 本文建立的某水陸兩棲飛機(jī)水面運(yùn)動的數(shù)學(xué)仿真方法，可以分析水陸兩棲飛機(jī)在水面滑行過程中受力和運(yùn)動狀態(tài)變量的特征，與水池試驗(yàn)結(jié)果的對比表明，該方法能夠反映飛機(jī)水面滑行過程中運(yùn)動參數(shù)的變化規(guī)律及過程，較為準(zhǔn)確地捕捉到了縱傾峰出現(xiàn)的狀態(tài)，可以用于型號飛機(jī)水面操縱特性條款的適航符合性計(jì)算分析、評估和改進(jìn)飛機(jī)設(shè)計(jì)方案、水面控制律設(shè)計(jì)。

(2) 本文建立的某水陸兩棲飛機(jī)地面運(yùn)動飛行力學(xué)仿真數(shù)學(xué)模型考慮了緩沖器、輪胎、支柱的動力學(xué)和運(yùn)動學(xué)關(guān)系。采用數(shù)字飛行仿真可以得到飛機(jī)地面起飛過程中飛機(jī)本體運(yùn)動狀態(tài)變量以及起落架各特征參數(shù)的時(shí)間歷程，該地面仿真方法的計(jì)算結(jié)果與飛機(jī)試飛結(jié)果吻合得較好，達(dá)到了工程應(yīng)用的精度要求，目前已應(yīng)用于型號飛機(jī)地面操縱特性的適航符合性評估、地面控制律設(shè)計(jì)、工程模擬器仿真、指導(dǎo)飛行員試飛操縱程序等方面。

在本文研究工作的基礎(chǔ)上，可以繼續(xù)開展波浪條件下的水動力數(shù)學(xué)建模，進(jìn)一步擴(kuò)大水面仿真的應(yīng)用范圍。