基于Laplace先驗和稀疏塊相關(guān)性的旋轉(zhuǎn)機械振動信號貝葉斯壓縮重構(gòu)
馬云飛, 白華軍, 溫亮, 郭馳名, 賈希勝
(1.武警士官學(xué)校 軍械系, 浙江 杭州 310023; 2.陸軍工程大學(xué)石家莊校區(qū) 裝備指揮與管理系, 河北 石家莊 050003)
0 引言
為了實時監(jiān)控裝備運行狀態(tài),利用分布式無線傳感技術(shù)實現(xiàn)機械信號傳輸、監(jiān)測,具有一定的應(yīng)用價值和發(fā)展?jié)摿ΑO鄬τ谟芯€的故障預(yù)測與健康管理系統(tǒng),無線監(jiān)測系統(tǒng)能夠大大增加靈活性、可維護(hù)性和可擴(kuò)展性[1]。而受無線傳輸帶寬限制,想要實時監(jiān)控必須對信號進(jìn)行壓縮傳輸。此前,有學(xué)者對結(jié)構(gòu)健康監(jiān)測領(lǐng)域的振動信號壓縮進(jìn)行了研究[2-3],但在該領(lǐng)域中進(jìn)行振動信號監(jiān)測的采樣頻率較低,信號壓縮實現(xiàn)相對較為容易。例如在橋梁結(jié)構(gòu)監(jiān)測中僅需要240 Hz的采樣頻率[4],而要想實現(xiàn)機械振動信號監(jiān)測,則至少需要5~20 kHz的采樣頻率[5]。由于機械振動信號具有非平穩(wěn)、非線性等特征,且設(shè)備運轉(zhuǎn)過程中會產(chǎn)生大量噪音,給信號壓縮帶來極大困難。
壓縮感知(CS)理論[6-8]近年來引起學(xué)者廣泛關(guān)注,其基本原理是利用與壓縮信號線性無關(guān)的觀測矩陣對稀疏信號進(jìn)行采樣,降低采樣信號維數(shù),并在接收端利用重構(gòu)算法估計原始信號。目前,基于CS的重構(gòu)算法可以歸為三類:凸優(yōu)化算法[9]、貪婪算法[10]、貝葉斯CS(BCS)算法[11]。BCS算法將貝葉斯估計原理與CS結(jié)合,利用稀疏貝葉斯模型中的相關(guān)向量機(RVM)[12]學(xué)習(xí)估計原始信號的最大后驗概率。BCS算法的優(yōu)點是充分考慮了信號傳輸中產(chǎn)生的噪音,且并不要求原始信號符合稀疏的性質(zhì)。此外,Babacan等[13]在BCS框架下,利用Laplace先驗代替高斯先驗約束未知信號,該先驗?zāi)軌蛟趯?shù)凹時最大程度地消除局部極小值,從而優(yōu)選接近于零的信號系數(shù)。Ji等[14]將單任務(wù)BCS擴(kuò)展為多任務(wù)BCS,通過挖掘多任務(wù)之間稀疏信號的統(tǒng)計相關(guān)性來實現(xiàn)多個稀疏信號聯(lián)合重構(gòu)。
對機械振動信號CS,文獻(xiàn)[15]提出對變分模態(tài)分解分量進(jìn)行CS,并通過循環(huán)模式矩陣定義新的觀測矩陣;文獻(xiàn)[16]將以往頻域稀疏化方法改為相空間稀疏化,并利用主成分分析提取特征,更有效促進(jìn)信號稀疏性;文獻(xiàn)[17]利用改進(jìn)m序列原理設(shè)計觀測矩陣電路實現(xiàn),并通過滾珠絲杠動態(tài)測試中的振動信號驗證了系統(tǒng)可行性。盡管上述研究取得了較好的效果,但是已有文獻(xiàn)缺乏機械振動信號的BCS相關(guān)研究,且沒有考慮到機械信號的內(nèi)部相關(guān)性。
本文提出一種基于Laplace先驗和稀疏塊相關(guān)性的BCS(Lap-CBCS)算法。由于Laplace先驗具有更好的稀疏促進(jìn)作用,特別適合于機械振動信號這一類復(fù)雜信號。建立基于該先驗的多任務(wù)BCS框架,并通過對模型中各信號塊共享的超參數(shù)進(jìn)行估計,實現(xiàn)信號重構(gòu)。改進(jìn)算法充分利用Laplace先驗的稀疏促進(jìn)作用和類周期信號的內(nèi)部相關(guān)性,以提高重構(gòu)的準(zhǔn)確性,為機械設(shè)備無線狀態(tài)監(jiān)測提供技術(shù)支撐。
1 CS與貝葉斯重構(gòu)
1.1 CS原理
CS[8]利用一個低維信號近似表達(dá)原始信號。假設(shè)原始信號為x(x∈RN,N為原始信號長度),稀疏變換為Ψ,觀測矩陣Φ∈RM×N(M?N,M為觀測矩陣行數(shù)或稱觀測次數(shù))。則信號x在該矩陣上的線性投影y∈RM可以作為壓縮信號,
y=Φx=ΦΨθ=Θθ,
(1)
式中:θ表示稀疏信號;Θ為傳感矩陣,Θ=ΦΨ.
由此,給出壓縮率定義:
(2)
由(2)式可知,原始信號越長,觀測次數(shù)越小,則壓縮率越高,也越難實現(xiàn)精確重構(gòu)。在y和Θ已知情況下,求解θ,可根據(jù)信號的稀疏性質(zhì),將信號重構(gòu)問題轉(zhuǎn)化為0-范數(shù)最優(yōu)化問題,即
min ‖θ‖0,
s.t.y=Θθ=ΦΨx.
(3)
該問題可利用基追蹤(BP)算法[8]、正交匹配追蹤(OMP)算法[10]求解。
1.2 貝葉斯重構(gòu)
1.2.1 問題轉(zhuǎn)化
BCS算法[11]從概率角度出發(fā),求解原始信號的最大后驗估計值,以恢復(fù)信號。令θs表示保留θ的M個最大分量、剩余分量置0的向量,θe表示保留剩余N-M個分量、其余分量置0的向量,則y可拆分成
y=Θθ=Θθs+Θθe=Θθs+ne,
(4)
式中:ne表示信號次要信息。
信號y傳輸過程中,可能存在噪音nm,則y表示為
y=Θθs+ne+nm=Θθs+n,
(5)
式中:n表示方差為σ2的零均值高斯噪聲。
1.2.2 構(gòu)造先驗分布
構(gòu)造y關(guān)于參數(shù)θs和σ2的先驗密度函數(shù):
(6)
RVM[12]是一個通用的貝葉斯框架,該框架使用參數(shù)中的線性模型來獲得回歸和分類任務(wù)的稀疏解。傳統(tǒng)模型采用分層先驗?zāi)P停⒓僭O(shè)θs的先驗分布為高斯分布。與該分布相比,Laplace先驗通過在軸上更多地使用后驗分布來嚴(yán)格約束稀疏性,因此信號系數(shù)更接近于0,本文假設(shè)其服從Laplace分布。
1.2.3 參數(shù)迭代求解
在RVM框架下如果y和超參數(shù)的先驗分布已知,可以得到θs的均值和方差表達(dá)式。進(jìn)一步,令超參數(shù)的邊緣分布最大,利用極大似然估計得到超參數(shù)更新表達(dá)式。通過反復(fù)迭代可估算出所有參數(shù)值,最后用θs的均值估計表示θs.
2 Laplace先驗和稀疏塊相關(guān)的BCS
2.1 基于Laplace分布的貝葉斯先驗?zāi)P?/h3>
在BCS領(lǐng)域應(yīng)用較多的是估計值服從高斯先驗的模型。研究表明,在實數(shù)域應(yīng)用高斯分布和指數(shù)分布共軛的Laplace先驗?zāi)P捅雀咚瓜闰灳哂懈玫南∈璐龠M(jìn)作用[13]。由于機械振動信號也是實數(shù)信號,可以用Laplace先驗約束。假設(shè)振動信號θs服從Laplace先驗,參數(shù)集γ=[γ1,γ2,…,γj,…,γN]。如圖1所示,Laplace分布可表示為高斯分布和指數(shù)分布的混合形式,結(jié)合對超參數(shù)γj的指數(shù)約束,得到θs關(guān)于λ的Laplace分布表達(dá)式為
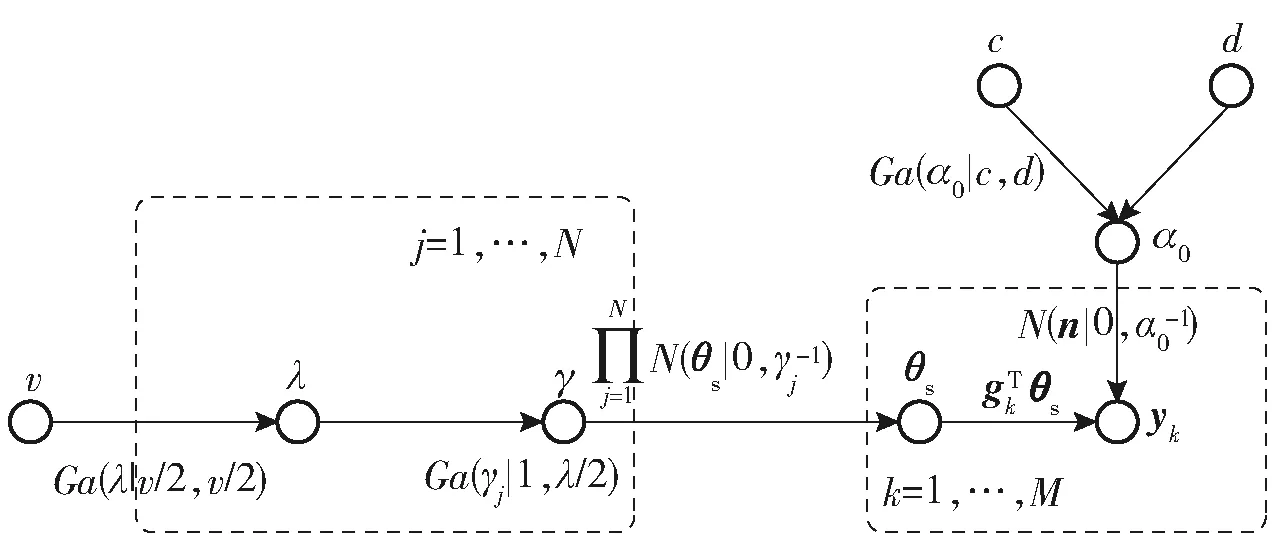
圖1 Laplace貝葉斯分級先驗?zāi)P虵ig.1 Laplace priors-based architectural model
(7)
式中:λ為Laplace模型中描述γj的超參數(shù);p(θs|γ)表示θs關(guān)于γ的先驗分布;p(γ|λ)表示γ關(guān)于λ的先驗分布;p(θs|λ)表示分層先驗分布。
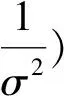
有關(guān)噪聲n的超參數(shù)α0=1/σ2仍服從Gamma分布。若給定γ、λ和σ2,則在已知觀測值y下的后驗概率分布可表示為p(θs,γ,λ,σ2|y)=p(θs|y,γ,λ,σ2)p(γ,λ,σ2|y)。其中p(θs|y,γ,λ,σ2)服從關(guān)于均值為μ、協(xié)方差為Σ的高斯分布,且有
μ=σ-2ΣΘTy,
(8)
Σ=(σ-2ΘTΘ+Λn-λ)-1,
(9)
式中:μ為θs的均值;Σ為θs的方差;Λn-λ=diag(1/γ1, 1/γ2,…,1/γj,…,1/γN)=diag{1/γj},該矩陣的估計依賴于超參數(shù)λ.由于p(γ,λ,σ2|y)∝p(γ,λ,σ2,y),求p(γ,λ,σ2,y)的解析式如下:
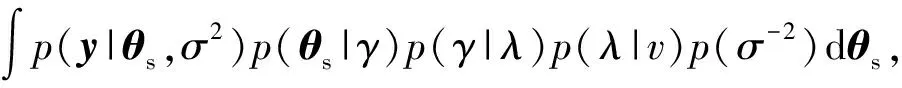
(10)
式中:p(y|θs,σ2)為y關(guān)于參數(shù)θs和σ2的先驗密度函數(shù);p(θs|γ)為θs關(guān)于參數(shù)γ的先驗密度函數(shù);p(γ|λ)為γ關(guān)于超參數(shù)λ的先驗密度函數(shù);p(λ|v)為λ關(guān)于超參數(shù)v的先驗密度函數(shù);p(σ-2)為σ2的先驗分布函數(shù)。
(10)式取對數(shù)并略去常數(shù)項后,分別對其求γj、λ、σ2偏導(dǎo)并令偏導(dǎo)等于0,根據(jù)超參數(shù)為正且v=0,解得γj的更新公式為
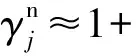
(11)
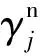
2.2 對多稀疏塊的Laplace BCS
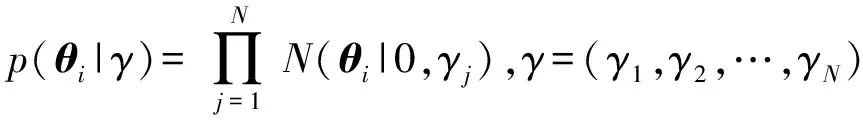
(12)
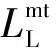
(13)
λn=2(N-1)/(Σjrj),
(14)
式中:μi,j表示第i塊數(shù)據(jù)中第j個參數(shù)γj的估計均值;Σi,jj表示第i塊數(shù)據(jù)的方差Σi的第j個對角線元素,其表達(dá)式見(9)式。利用(13)式、(14)式迭代計算復(fù)雜度較高,本文采用文獻(xiàn)[14]的快速RVM算法。
3 基于Lap-CBCS算法的機械振動信號壓縮重構(gòu)
類似于機器學(xué)習(xí)中每次訓(xùn)練樣本都會對模型參數(shù)進(jìn)行優(yōu)化,對于多數(shù)據(jù)塊的壓縮重構(gòu)也是如此。Lap-CBCS算法參考多任務(wù)貝葉斯估計,將多塊數(shù)據(jù)看作多任務(wù)貝葉斯中的任務(wù),構(gòu)建稀疏塊Laplace先驗分布模型,使得每塊數(shù)據(jù)都能夠?qū)ο闰灧植紖?shù)進(jìn)行改進(jìn),就可以促進(jìn)各塊的稀疏重構(gòu),大大提高貝葉斯參數(shù)估計的準(zhǔn)確性。但想要將Lap-CBCS算法應(yīng)用到實際機械振動信號的壓縮重構(gòu)中,還需要解決信號分塊和稀疏域選取兩個問題。
3.1 機械振動信號的周期性分塊
由于齒輪箱振動信號具有非線性、非平穩(wěn)性,其周期性表現(xiàn)得并不明顯,可稱其為類周期性。機械振動信號的類周期確定主要有如下3種方法:
1)根據(jù)轉(zhuǎn)速和采樣頻率計算類周期。假設(shè)轉(zhuǎn)速n=600 r/min,采樣頻率Fs=5 kHz,即采樣點數(shù)為5 000個/s,周期T=Fs/n=5 000/10=500個,由此可得每500個采樣點為一個類周期。
2)通過頻譜分析確定。可以利用傅里葉變換得到信號頻譜圖,分析信號頻譜圖,得出信號類周期。
3)通過包絡(luò)線確定。首先對信號作自相關(guān)分析,并求得自相關(guān)信號包絡(luò)線。然后取包絡(luò)線上相鄰兩峰值之間的距離作為類周期。
對機械振動信號進(jìn)行傅里葉變換后會出現(xiàn)大量的頻譜峰值,難以識別類周期。而通過求包絡(luò)線計算誤差也較大,還需要對多個候選值求平均。因此,本文采用通過轉(zhuǎn)速和采樣頻率計算類周期的方法,轉(zhuǎn)速信息可通過轉(zhuǎn)速傳感器測得。
3.2 稀疏域選取
常見稀疏變換方法有離散余弦變換、小波變換等,稀疏域選取可根據(jù)信號稀疏度和相似度確定。
定義1稀疏度。假設(shè)原始信號x(x∈RN)在某變換域Ψ上是稀疏的,則稀疏信號θ與原始信號關(guān)系為x=Ψθ,變換后信號的0-范式‖Ψ-1x‖0,且Ψ-1x∈RM,則稀疏度可表示為K=‖Ψ-1x‖0/M.
定義2相似度。假設(shè)函數(shù)R(s,t)={δ|如果|si-ti|>ε則δi=1,否則δi=0,i=0,1,2,…,N},其中ε為閾值,則兩組信號x1,x2∈RN的相似度可表示為D=1-‖R(Ψ-1x1,Ψ-1x2)‖0/M.
3.3 機械振動信號壓縮重構(gòu)流程
本文提出了基于Laplace先驗和稀疏塊相關(guān)性的機械振動信號壓縮重構(gòu)方法(見圖2),具體包括以下步驟:
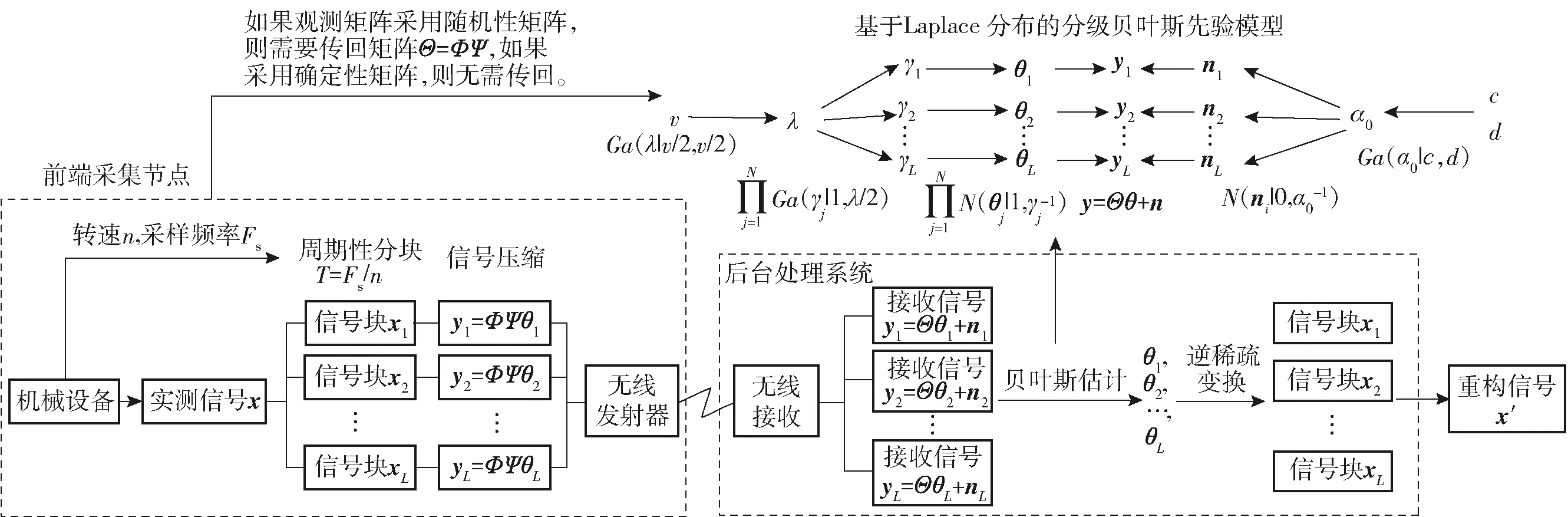
圖2 基于Laplace-CBCS算法的機械振動信號壓縮重構(gòu)流程Fig.2 Compression and reconstruction processes of mechanical vibration signal based on Laplace-CBCS algorithm
步驟1周期性分塊。根據(jù)類周期對采集到的振動信號進(jìn)行周期性分塊。利用轉(zhuǎn)速n和采樣頻率Fs計算類周期,計算公式為T=Fs/n.
步驟2信號壓縮。由于機械振動信號是一類非平穩(wěn)復(fù)雜信號,為了提高其稀疏度,首先利用稀疏基Ψ將該信號投影到稀疏域,令原始信號x=Ψθ,得到稀疏域信號θ.利用傳感矩陣Θ=ΦΨ對稀疏信號進(jìn)行狀態(tài)壓縮,得到壓縮后信號y=Θθ.
步驟3信號分塊傳輸。分別傳輸并接收分塊處理后的信號y1,…,yL.
步驟4x信號重構(gòu)。利用本文Lap-CBCS重構(gòu)算法以及從前端采集節(jié)點傳回的傳感矩陣Θ1,…,ΘL(如果觀測矩陣是確定性矩陣則無需傳回,如果是隨機性矩陣則需要傳回)對y1,…,yL聯(lián)合重構(gòu),得到稀疏信號θ1,…,θL.對稀疏信號進(jìn)行逆稀疏變換,得到原始分塊信號x1,…,xL,將原始信號塊按順序拼接在一起,得到完整重構(gòu)信號x′.重構(gòu)信號與原始信號相比相位不發(fā)生變化。
4 齒輪箱數(shù)據(jù)實驗驗證
4.1 實驗準(zhǔn)備
如圖3所示,實驗齒輪箱型號為JZQ175,三相電磁調(diào)速電動機功率4 kW,風(fēng)冷磁粉制動器為齒輪箱提供載荷。數(shù)據(jù)采集由美國DYTRAN公司生產(chǎn)的4個3056B4型壓電傳感器組成。利用上述設(shè)備進(jìn)行齒輪箱預(yù)制故障實驗,轉(zhuǎn)速800 r/min,輸入端負(fù)載10 N·m,采樣頻率20 kHz,采樣時間為6 s. 將上述實驗環(huán)境下采集到的數(shù)據(jù)進(jìn)行信號壓縮、傳輸,重構(gòu)仿真實驗。仿真環(huán)境為:MATLAB 2017b,Win10操作系統(tǒng),i5-8250 CPU.

圖3 實驗臺示意圖Fig.3 Test-rig of gearbox
預(yù)置故障實驗主要包括兩種:齒根裂紋故障實驗和斷齒故障實驗。齒根裂紋故障加工在輸出軸大齒輪齒根上,斷齒故障加工在中間軸大齒輪上。本文進(jìn)行4種預(yù)置故障實驗:正常狀態(tài)、1 mm齒根裂紋故障、2 mm齒輪斷齒故障、2 mm齒根裂紋故障(1 mm、2 mm表示裂紋深度),采樣時間為6 s,采樣點數(shù)120 000,采集到的數(shù)據(jù)如圖4所示。
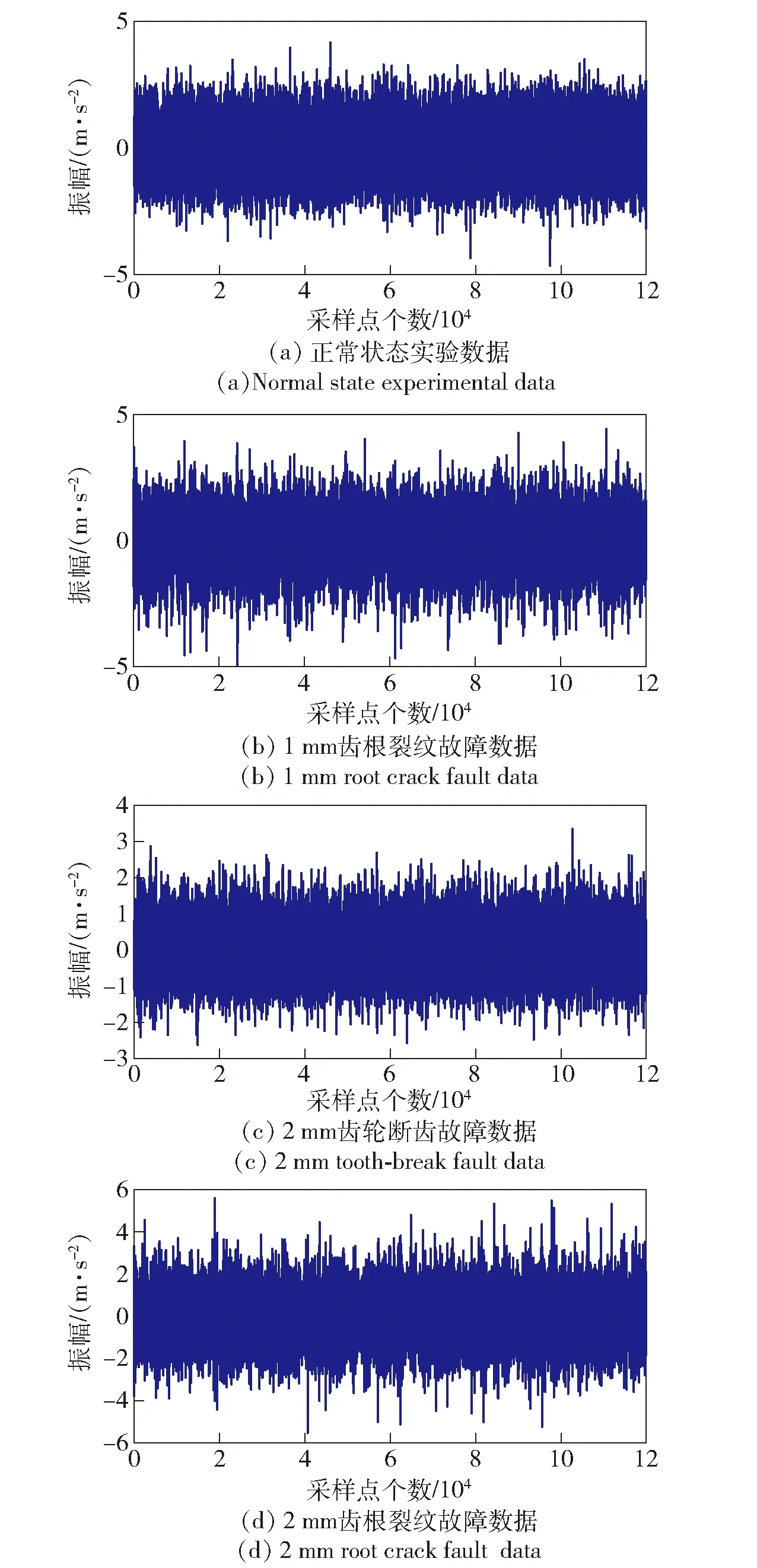
圖4 齒輪箱實測振動信號Fig.4 Measured vibration signals of gearbox
4.2 1 mm齒根裂紋故障仿真實驗
4.2.1 根據(jù)轉(zhuǎn)速和采樣頻率計算類周期

圖5 轉(zhuǎn)速信號Fig.5 Tachometer signal
4.2.2 稀疏域選擇
針對實測數(shù)據(jù),分析離散余弦變換以及小波變換處理后稀疏信號的稀疏度與相似度。觀察處理數(shù)據(jù)發(fā)現(xiàn),小波分解層數(shù)對于變換后信號的稀疏性、相似性影響都不大。而對于稀疏信號,稀疏度越小,相似度越高,越容易進(jìn)行信號恢復(fù)。仿真實驗結(jié)果表明:離散余弦變換作為稀疏變換的處理效果是最好的。
4.2.3 利用Lap-CBCS算法對1 mm齒根裂紋故障數(shù)據(jù)進(jìn)行仿真實驗
為對比分析,先利用BCS算法對80塊信號分別壓縮重構(gòu),再利用Lap-CBCS算法對80塊信號聯(lián)合壓縮重構(gòu),對比兩次重構(gòu)。此外,本文擬采用標(biāo)準(zhǔn)均方根誤差(MSE)作為重構(gòu)效果評價指標(biāo),其計算公式如(15)式所示:
MSE=‖u-u′‖2/‖u‖2,
(15)
式中:u表示原始信號;u′表示重構(gòu)信號。
如圖6所示,隨機選取第1、15、22、36、61塊數(shù)據(jù)進(jìn)行比較分析,發(fā)現(xiàn)BCS方法對每塊信號單獨壓縮重構(gòu)MSE大于0.8,而利用Lap-CBCS算法重構(gòu)可將MSE降低到0.3左右。
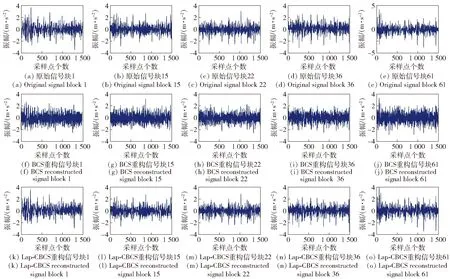
圖6 實測齒輪箱1 mm裂紋數(shù)據(jù)壓縮重構(gòu)效果對比(80塊信號聯(lián)合重構(gòu))Fig.6 Comparison results of reconstructing signal blocks for measured 1 mm crack on root of tooth (simultaneous construction of 80 signal blocks)
將Lap-CBCS算法重構(gòu)的80塊信號拼接起來,可以得到完整重構(gòu)信號。由于實驗采樣點數(shù)較多,無法看出重構(gòu)細(xì)節(jié),選擇采樣點1×104~2×104的數(shù)據(jù)觀察細(xì)節(jié)。如圖7所示,Lap-CBCS重構(gòu)數(shù)據(jù)點基本能夠覆蓋原數(shù)據(jù)點。在該范圍內(nèi),進(jìn)一步選擇出1.1×104~1.2×104的數(shù)據(jù)觀察,發(fā)現(xiàn)Lap-CBCS算法重構(gòu)只有在局部極值點處與原數(shù)據(jù)略有偏差,其余數(shù)據(jù)點基本重構(gòu)成功。
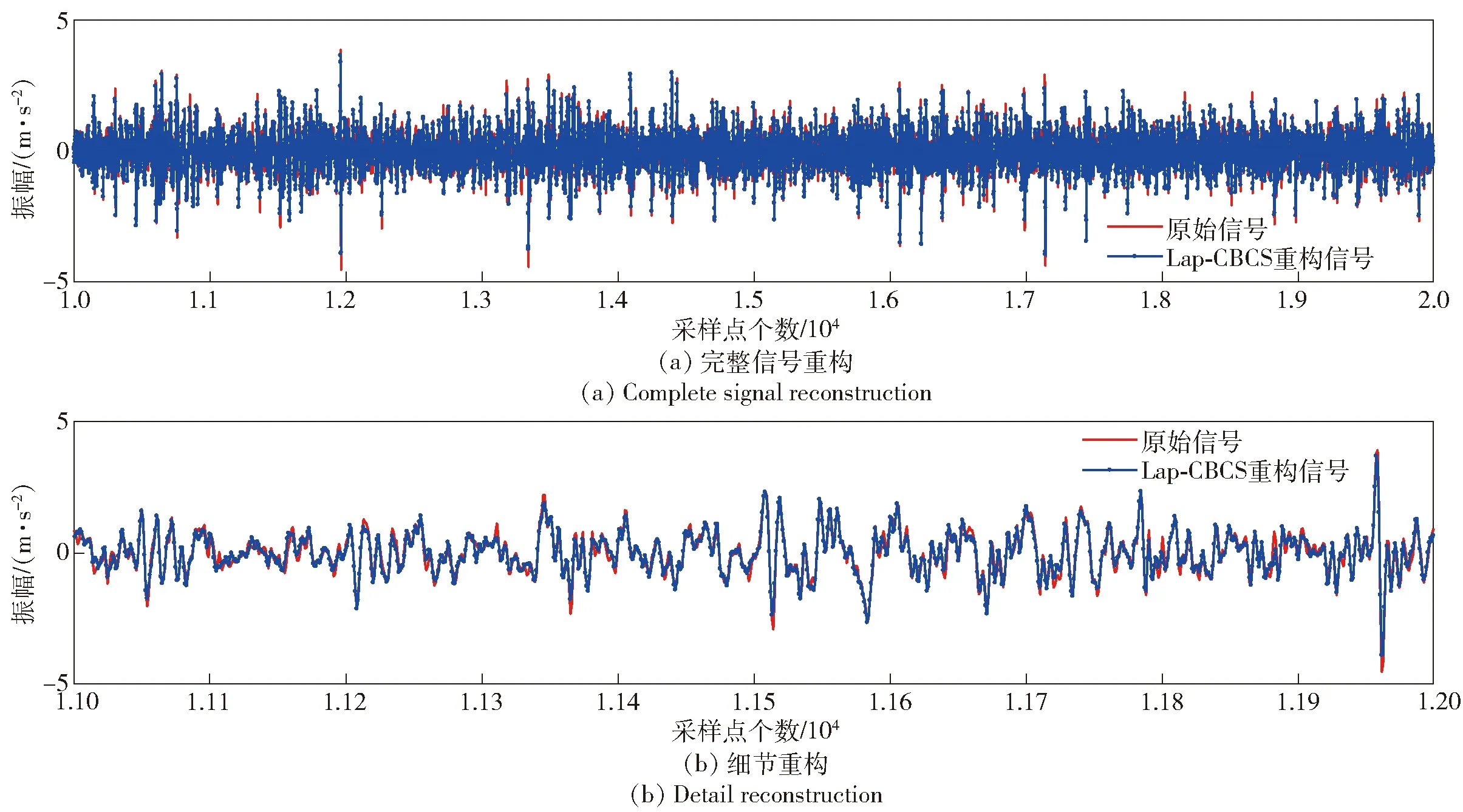
圖7 實測齒輪箱1 mm裂紋局部數(shù)據(jù)重構(gòu)細(xì)節(jié)Fig.7 Details of local data reconstruction for measured 1 mm crack
4.2.4 與其他算法對比
本文利用BP、OMP算法針對上述齒輪箱1 mm齒根裂紋故障數(shù)據(jù)進(jìn)行重構(gòu)實驗。實驗結(jié)果表明BP、OMP、BCS算法的標(biāo)準(zhǔn)MSE都在0.5以上,而Lap-CBCS算法的MSE能保持在0.3左右。此外,分析4種算法運行時間發(fā)現(xiàn)OMP算法所需時間最少,其次是BP算法,而Lap-CBCS算法運行時間最長。
4.3 齒輪不同故障狀態(tài)實驗
選取另外3種狀態(tài):正常運行、2 mm齒輪斷齒故障、2 mm齒根裂紋故障下的實驗數(shù)據(jù),由于轉(zhuǎn)速和采樣頻率不變,分塊周期仍為1 500數(shù)據(jù)點。對每種狀態(tài)數(shù)據(jù)分別利用BCS、Lap-CBCS、BP、OMP 4種算法進(jìn)行壓縮重構(gòu)分析。
選取觀測次數(shù)400、700、1 000(對應(yīng)壓縮率3.75、2.14、1.50),對每種不同狀態(tài)數(shù)據(jù)計算出MSE和運行時間平均值,得到表1所示結(jié)果。
由表1可見4種算法的標(biāo)準(zhǔn)MSE存在如下關(guān)系:MSELap-CBCS 表1 不同齒輪箱狀態(tài)下重構(gòu)算法MSE與運行時間對比Tab.1 Calculated MSEs and running times of different algorithms under different gearbox conditions 1)隨著壓縮率降低,CS算法MSE降低,且算法運行時間增加。其中MSELap-CBCS最低,在壓縮率為2.14和1.5時可基本實現(xiàn)重構(gòu)(MSE不大于0.3),而BP、BCS算法只有在壓縮率1.5時才能實現(xiàn)重構(gòu)(齒根裂紋故障狀態(tài)下仍不能實現(xiàn)重構(gòu))。另外,如果使用OMP算法則MSEOMP較大,表明該算法對于復(fù)雜機械振動信號這類非稀疏信號較為敏感,不適用于復(fù)雜齒輪箱數(shù)據(jù)的重構(gòu)。 2)Lap-CBCS算法運行時間較長,對計算資源要求高。盡管如此,考慮到振動信號傳輸?shù)缴衔粰C后后臺可利用的計算資源較多,且在某些特定場景下需要高精度的信號重構(gòu)技術(shù),因此Lap-CBCS算法具有較好的應(yīng)用價值。 本文將Laplace先驗?zāi)P秃驼駝有盘栔芷谛韵∈鑹K相結(jié)合,提出一種改進(jìn)的BCS方法。針對機械振動信號,提出利用轉(zhuǎn)速和采樣頻率計算類周期進(jìn)行周期性分塊,并給出振動信號壓縮重構(gòu)流程。所得主要結(jié)論如下: 1)齒輪箱實測信號驗證結(jié)果表明,盡管Lap-CBCS運行時間較長,但在標(biāo)準(zhǔn)MSE方面優(yōu)于BCS、BP、OMP 3種典型算法。 2)Lap-CBCS方法較好地解決了復(fù)雜非平穩(wěn)信號的壓縮重構(gòu)問題,對于機械設(shè)備的無線監(jiān)測具有一定的促進(jìn)意義。 但是,Lap-CBCS算法雖然重構(gòu)精度較高,卻需要較長的運行時間。如何改進(jìn)算法、提高計算效率,將是下一步可能的研究方向。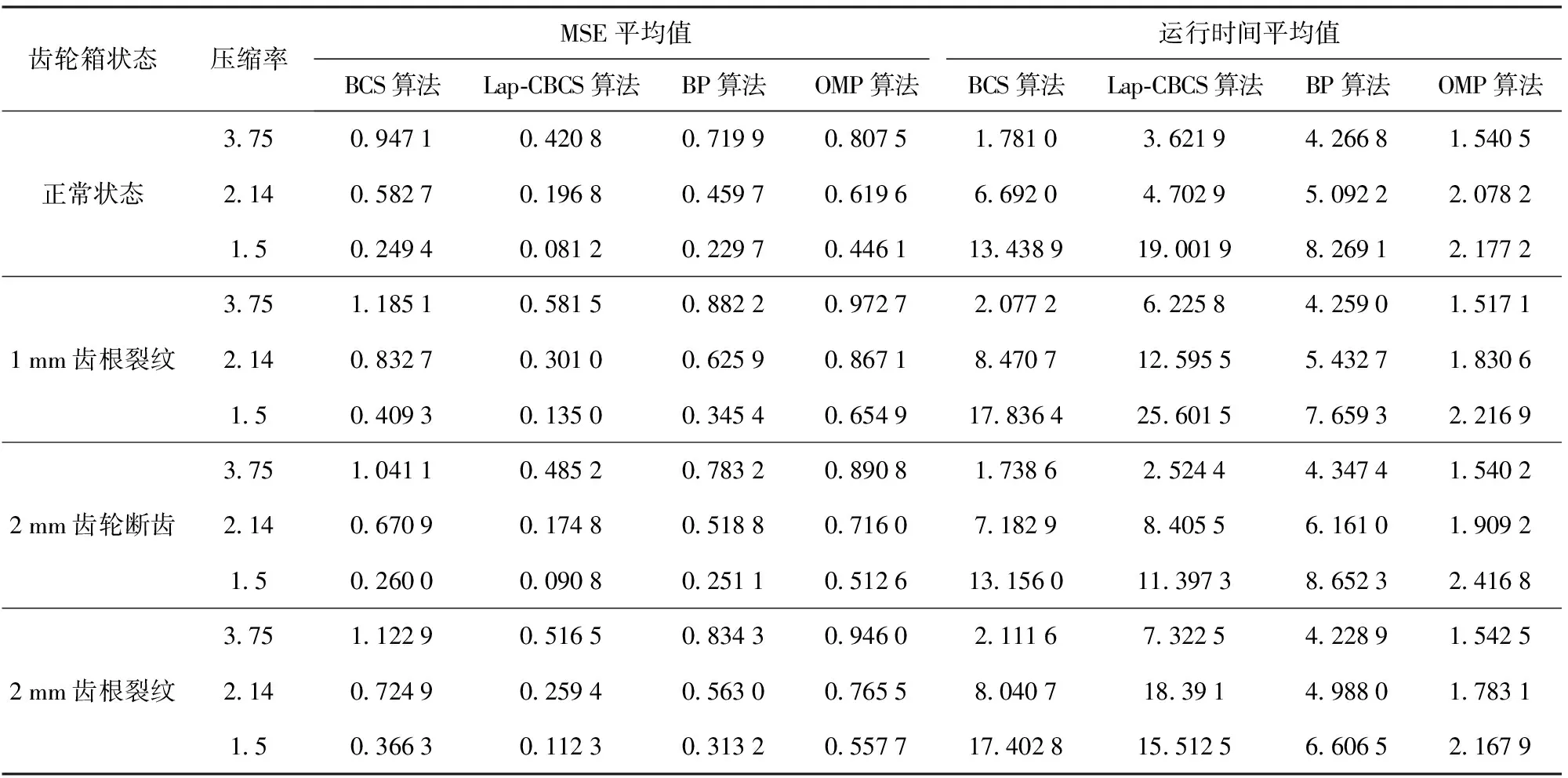
5 結(jié)論

