桌面式航空彈藥測試模擬訓(xùn)練設(shè)備效能評估

周弘揚(yáng)，馬 超，高 松

(空軍勤務(wù)學(xué)院 航空彈藥保障系， 江蘇 徐州 221000)

航空彈藥測試設(shè)備的操作與維護(hù)內(nèi)容復(fù)雜，但由于實(shí)裝數(shù)量少、維護(hù)成本高以及彈藥通電壽命有限等原因，致使訓(xùn)練受到嚴(yán)格限制，無法有效提高保障人員的能力水平。而桌面式測試模擬訓(xùn)練設(shè)備是以操作使用為仿真對象，以計算機(jī)為平臺，應(yīng)用系統(tǒng)仿真技術(shù)和虛擬現(xiàn)實(shí)技術(shù)研制的一種人在回路中的、桌面式的虛擬仿真系統(tǒng)，用于對個人和小組進(jìn)行檢測、故障診斷等程序化操作訓(xùn)練和教學(xué)中。不同于“看得見的實(shí)裝”和“看不見的仿真系統(tǒng)”組合的半實(shí)裝模擬訓(xùn)練設(shè)備[1]，桌面式設(shè)備能夠有效減少實(shí)裝磨損和彈藥通電測試壽命損耗問題且具有不受場地和天氣限制、結(jié)構(gòu)簡單、成本低、方便高效等特點(diǎn)。其設(shè)備效能的高低對場站勤務(wù)保障能力生成起著至關(guān)重要的作用，因此對其效能的評估十分必要。

目前，針對模擬訓(xùn)練設(shè)備的研究主要集中在技術(shù)能力提升和標(biāo)準(zhǔn)規(guī)范上，包括外軍正積極推進(jìn)模擬系統(tǒng)數(shù)據(jù)、模型、接口、軟件研制的互聯(lián)互通和一體化試訓(xùn)平臺的應(yīng)用[2]。但對于設(shè)備保障效能的研究，文獻(xiàn)[3]針對船舶電力系統(tǒng)模擬訓(xùn)練提出層次分析法賦權(quán)，建立綜合模糊評判模型。文獻(xiàn)[4]則考慮專家對方法的偏好，在AHP、比系數(shù)法、熵權(quán)法中比較確定權(quán)重。文獻(xiàn)[5]提出基于Petri網(wǎng)的模擬訓(xùn)練評估模型。文獻(xiàn)[6]構(gòu)建灰色AHP模型，利用神經(jīng)網(wǎng)絡(luò)非線性擬合求解效能等等。這些方法在一定程度上反映了特定環(huán)境下的效能[7，8]，但在處理定量定性聯(lián)合評估問題時都存在一定的局限性，如神經(jīng)網(wǎng)絡(luò)要大量的訓(xùn)練數(shù)據(jù)，模糊、灰色理論主觀性大、函數(shù)復(fù)雜[9-12]，處理模擬訓(xùn)練設(shè)備效能評估不太理想。

本文提出一種基于D-AHP(D數(shù)理論改進(jìn)的層次分析法)和云模型相結(jié)合的評估方法。D數(shù)理論是鄧勇教授2012年提出[13]，允許指標(biāo)元素之間不獨(dú)立的情況出現(xiàn)，處理不完備不確定信息能力強(qiáng)。結(jié)合AHP解決多層次、多目標(biāo)的大系統(tǒng)優(yōu)化問題時靈活、簡潔的特點(diǎn)[14]，云模型依靠簡單的計算期望、方差和高階中心矩將定性與定量模型相統(tǒng)一，使評價結(jié)果更接近實(shí)際情況[15，16]。兩者的結(jié)合為測試模擬訓(xùn)練設(shè)備效能評估提供新的思路。

1 航空彈藥測試模擬訓(xùn)練設(shè)備概述

航空彈藥測試模擬訓(xùn)練系統(tǒng)組成如圖1所示，包括多媒體教學(xué)和模擬訓(xùn)練系統(tǒng)兩大部分。

多媒體教學(xué)系統(tǒng)采用圖像、文字、動畫等多媒體形式將設(shè)備工作原理、彈藥及結(jié)構(gòu)組成和操作使用維護(hù)的示教等信息呈現(xiàn)在終端。

模擬訓(xùn)練系統(tǒng)則主要由視景仿真、測試過程仿真、音響仿真、故障仿真、數(shù)據(jù)庫等模塊組成，用于實(shí)現(xiàn)彈藥的測試、信息判讀和故障診斷等訓(xùn)練以及實(shí)現(xiàn)成績的評定和記錄回放等功能，有助于彈藥大隊人員提高測試保障水平。

圖1 桌面式測試模擬訓(xùn)練系統(tǒng)結(jié)構(gòu)組成框圖

2 測試訓(xùn)練設(shè)備評估模型建立

2.1 指標(biāo)體系構(gòu)建

桌面式航空彈藥測試模擬訓(xùn)練系統(tǒng)不同于數(shù)字計算機(jī)仿真，應(yīng)具有良好的通用性、交互性、可操作性以及較好的仿真度等才能符合訓(xùn)練要求。其設(shè)備效能既與系統(tǒng)本身的技術(shù)性能有關(guān)，又涉及成績評估等方面，因此信息具有一定的模糊性。基于此，本文從訓(xùn)練設(shè)備要素出發(fā)，遵循全面性、重要性、層次性原則，通過查閱文獻(xiàn)和咨詢裝備保障領(lǐng)域?qū)＜业姆绞剑⑷鐖D2所示指標(biāo)體系，主要包含硬件性能、訓(xùn)練能力、軟件性能、系統(tǒng)可用性等指標(biāo)。

圖2 桌面式測試模擬訓(xùn)練設(shè)備效能評價指標(biāo)體系框圖

2.2 D-AHP賦權(quán)

由于AHP將指標(biāo)體系結(jié)構(gòu)內(nèi)元素兩兩比較確定權(quán)重方法非常實(shí)用，但信息的模糊性又限制了典型AHP方法的使用。因此提出D數(shù)偏好關(guān)系改進(jìn)AHP的方法，減少不確定性。

D數(shù)理論是對D-S證據(jù)理論的改進(jìn)，無需計算概率且可以解決不確定性問題，在應(yīng)急事件管理能力評估、信息安全風(fēng)險評估等方面有較好應(yīng)用[13]。

關(guān)于D數(shù)的相關(guān)定義和性質(zhì)如下：

定義1設(shè)存在非空有限集Ω與映射D：

Ω→D[0，1]

(1)

滿足：

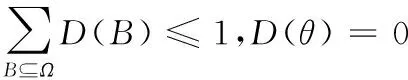
(2)

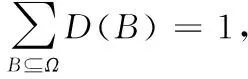
定義2設(shè)存在D數(shù)和非空有限集Ω，則D數(shù)信息完整度Q可量化為：

(3)

定義3設(shè)離散非空有限集Ω={b1，b2…，bn}，D數(shù)特殊表達(dá)式為：

D={(b1，υ1)，(b2，υ2)，…，(bn，υn)}

(4)

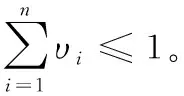
定義4設(shè)存在D數(shù)：

D={(b1，υ1)，(b2，υ2)，…，(bn，υn)}，則其集成為：

(5)

定義5模糊偏好關(guān)系用符號“?”表示，專家對各評估對象的偏好依據(jù)對比較矩陣來表示。

設(shè)存在一組評估對象F={F1，F(xiàn)2，…，F(xiàn)n}，其模糊偏好關(guān)系為：

UR∶F×F→[0，1]

(6)

用矩陣表示為R=[rij]n×n：

(7)

該矩陣滿足：

1)rij≥0；rij+rji=1， ?i，j∈{1，2，…，n}；

2)rij=0.5， ?i∈{1，2，…，n}。

矩陣元素rij表示評估專家認(rèn)為Fi相對與Fj的重要程度，其賦值范圍及其含義如下：

rij=UR(Fi，F(xiàn)j)

(8)

如果rij=0，則Fj明顯比Fi重要。

如果0

如果rij=0.5，則Fj與Fi無差別。

但該方法存在專家評估信息不完整或不確定的情況，無法構(gòu)造出合理的偏好矩陣。

因此對偏好關(guān)系改進(jìn)，將適用范圍擴(kuò)大到不確性的信息領(lǐng)域。其評判矩陣則被稱D矩陣。

定義6設(shè)一組評估樣本F={F1，F(xiàn)2，…，F(xiàn)n}，則D數(shù)偏好關(guān)系為：

RD∶F×F→D

(9)

以矩陣形式表示為RD=[Dij]n×n。其中：

關(guān)于D數(shù)偏好關(guān)系計算權(quán)重的步驟為：

1) 組織領(lǐng)域?qū)＜覍χ笜?biāo)成對比較，以偏好關(guān)系形式表示其重要度，構(gòu)建D矩陣RD。

根據(jù)設(shè)備效能評價指標(biāo)體系，確定準(zhǔn)則層一級指標(biāo)集為A={A1，A2，A3，A4}={硬件性能，軟件性能，訓(xùn)練能力，設(shè)備可用性}。

為定量表示指標(biāo)間相對重要性，采用0.1～0.9標(biāo)度進(jìn)行成對比較賦值。其對應(yīng)含義如表1所示。

表1 評估標(biāo)準(zhǔn)及含義

2) 由I(D)，將矩陣RD表示成確定數(shù)矩陣RC。

3) 計算偏好概率，構(gòu)建基于矩陣RC的概率矩陣RP。

因此，其不一致系數(shù)為0.183 3，經(jīng)專家評估認(rèn)為該系數(shù)在可接受范圍內(nèi)。因此對一級指標(biāo)排序?yàn)锳2>A3>A4>A1，對設(shè)備效能影響從高到低分別為：軟件性能，訓(xùn)練能力，設(shè)備可用性，硬件性能。

(10)

其中，ωAi表示第i個準(zhǔn)則層一級指標(biāo)權(quán)重，λ表示評估信息的可信度，取值與專家經(jīng)驗(yàn)和對問題背景的認(rèn)知水平有關(guān)。根據(jù)文獻(xiàn)[13]給出的取值及說明可知，專家經(jīng)驗(yàn)豐富，因此λ為2，則一級權(quán)重向量為ωA=(0.212 5，0.362 5，0.262 5，0.162 5)。

同理，可求得各二級指標(biāo)相對于一級指標(biāo)的權(quán)重以及相對于評估目標(biāo)的綜合權(quán)重，如表2所示。

表2 指標(biāo)權(quán)重計算結(jié)果

2.3 云模型標(biāo)準(zhǔn)量化

李德毅院士把概率論中的數(shù)字特征用期望、方差和高階中心矩表示，將模糊數(shù)學(xué)中較精確的隸屬度和利用兩種精確集合函數(shù)評定不確定性的粗糙集等模型優(yōu)勢結(jié)合提出云模型理論，使評價結(jié)果更接近實(shí)際情況[15-16]。

云模型用期望Ex、熵En和超熵He三個數(shù)值來表示數(shù)字特征：

Ex是數(shù)值域中最能代表其定性評估值的樣本值即云重心；

En是對模糊度的評估，反映數(shù)值域中隨機(jī)值在云中的范圍，表示被定性云滴的離散程度；

He是云滴的不確定度的評估，是熵的疊加。超熵越大，云層越厚，隸屬度的不確定性也越大。

根據(jù)云理論和專家意見，將評估標(biāo)準(zhǔn)定義為5種：優(yōu)、良、中、及格和差。量化標(biāo)準(zhǔn)如表3所示。

表3 桌面式測試模擬訓(xùn)練設(shè)備效能評估的量化標(biāo)準(zhǔn)

3 實(shí)例應(yīng)用

以某型空空導(dǎo)彈通用測試模擬訓(xùn)練設(shè)備為研究對象，在實(shí)地問卷調(diào)查、座談的基礎(chǔ)上收集相關(guān)數(shù)據(jù)，進(jìn)行如下評估工作。

1) 根據(jù)評價標(biāo)準(zhǔn)(見表3)，結(jié)合五位專家意見得到指標(biāo)層評價指標(biāo)結(jié)果如表4，表4中每行表示一位專家對指標(biāo)的評價，每列表示同一項指標(biāo)不同專家的評價。

2) 運(yùn)用云理論，按照指標(biāo)層期望、熵、超熵計算式(11)得到指標(biāo)層各項指標(biāo)特征值，如表5。

(11)

3) 根據(jù)指標(biāo)層云數(shù)字特征值，按照指標(biāo)權(quán)重式(12)計算，得到準(zhǔn)則層各項評價結(jié)果，如表6。

(12)

表4 指標(biāo)層評價指標(biāo)結(jié)果

表5 指標(biāo)層云模型各項指標(biāo)特征值

表6 準(zhǔn)則層云模型各項指標(biāo)特征值

4) 由于準(zhǔn)則層權(quán)重系數(shù)為：

WA=(0.212 5，0.362 5，0.262 5，0.162 5)

因此，可以得到目標(biāo)層綜合效能評估云數(shù)字特征為(0.465 3，0.089 4，0.025 3)。與效能評估標(biāo)準(zhǔn)相比較，可知總體水平“及格”。其中，模擬逼真度、經(jīng)濟(jì)性的云數(shù)字特征分別為B5(0.4，0.050 1，0.049 9)、B14(0.4，0.100 3，0.007 3)，其評估結(jié)果的平均值小于綜合效能評估值，說明這兩方面的指標(biāo)落后于系統(tǒng)整體性能，制約著該款空空導(dǎo)彈通用測試模擬訓(xùn)練設(shè)備效能的提升。因此在后期研制升級過程中著重提高仿真環(huán)境真實(shí)度和節(jié)約成本，從而提高設(shè)備訓(xùn)練能力。

4 結(jié)論

通過D數(shù)理論改進(jìn)AHP和云模型評價相結(jié)合，既體現(xiàn)了專家的集體智慧也較好的反映了桌面式航空彈藥測試模擬訓(xùn)練設(shè)備的實(shí)際情況，為客觀、準(zhǔn)確地對模擬訓(xùn)練設(shè)備效能評估提供了新思路，可有效提高勤務(wù)保障能力，也為系統(tǒng)研制升級提供了重要參考意見。