基于能力培養的線性代數課程內容優化設計
劉 焱
[山東協和學院基礎部(思政部),濟南 250109]
1 專業課與線性代數的對接
1.1 行列式部分內容的優化
行列式是線性代數的重要組成部分,是解線性方程組的重要工具,而線性方程組在經濟領域非常重要,比如經濟中的成本問題、利潤問題。以成本問題為例,一次投入一批材料會生產出不同的幾種產品,現需要核算每種產品的成本。這種情況可以通過生產幾次進行測驗,比如第一批生產A、B產品分別是20 kg、30 kg,總成本500元,第二批生產A、B產品分別是40 kg、20 kg,總成本600元,求每種產品的單位成本。
解:設A、B兩種產品單位成本分別為x,y,列方程組如下:
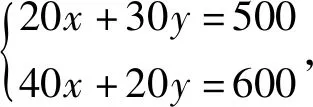
因此,在講授行列式相關問題時,適當加入以上類似的經濟類問題,使得學到的知識學以致用,能夠大大提高學生的學習興趣。
1.2 矩陣計算部分內容的優化
線性代數內容中最基礎、最重要、內容最多的是矩陣。矩陣是線性代數內容中最基本的概念,矩陣的運算是線性代數非常重要的內容。矩陣被廣泛應用于各個領域,在物理學中,矩陣于力學、量子力學、光學和電路學中都有應用。互聯網背景下,矩陣也在計算機編程、三維動畫制作中起到很大的作用。一些特殊矩陣如稀疏矩陣、準對角矩陣、單位矩陣、零矩陣有更簡單的計算方法。矩陣的運算在數學計算領域具有重要作用,大大提高了矩陣的利用率。在實際生活中,矩陣理論和矩陣的計算無處不在,例如萊斯利人口模型中矩陣冪運算的應用,經濟管理問題中的生產成本會用到矩陣乘法運算,希爾密碼會用到逆矩陣和矩陣乘法運算等,很多領域都和矩陣密切相關。
第一,矩陣乘法的應用——生產成本問題。
某工廠生產三種產品,每種產品的原料費、工資支付、管理費等見表1。每季度生產每種產品的數量見表2。
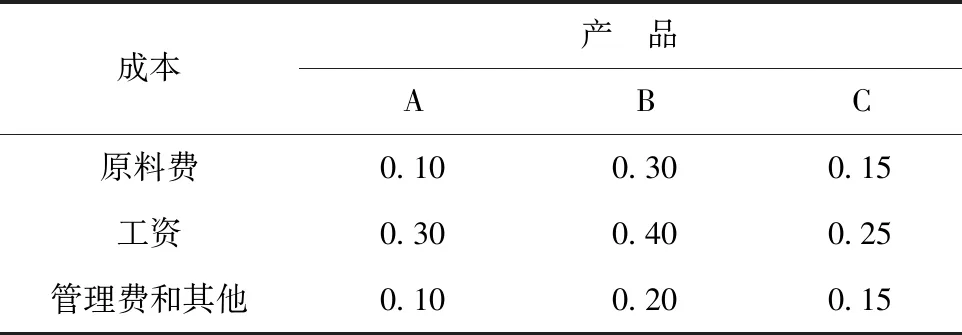
表1 生產單位產品的成本(美元)Tab.1 Cost of unit product(dollar)
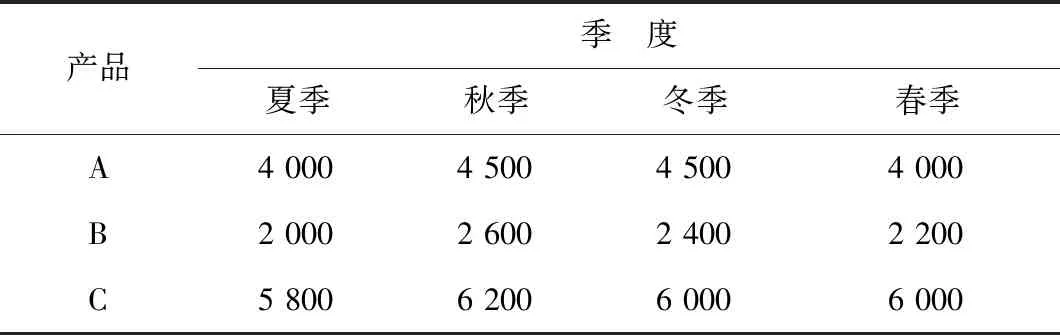
表2 每季度產量Tab.2 Quarterly production
用矩陣的方法考慮這個問題,這兩張表格中的數據均可表示為一個矩陣,計算MP得:

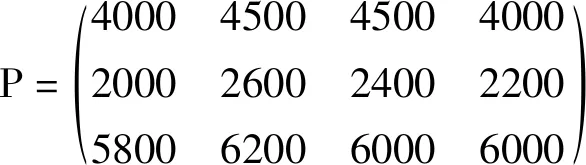
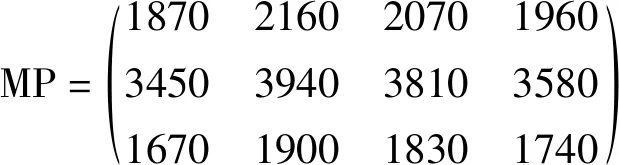
MP的四列分別表示夏、秋、冬、春四季生產三種產品的總成本。MP三行分別表示四個季度中每一季度原料的總成本、工資的總成本、管理的總成本。
第二,逆矩陣的應用——應用矩陣編制Hill密碼。
古代戰爭中,為了避免信息泄露開始啟用暗語,后期軍事信息的傳遞更加謹慎精密。1929年,Lester·Hill通過矩陣理論發明了非常經典的希爾密碼。希爾密碼是利用了基本矩陣原理的替換密碼,主要通過運用矩陣的乘法對所傳輸信息進行加密處理,然后利用逆矩陣進行解密,矩陣的運用在信息加密中得到明顯體現。隨著科技和信息化的高速發展,密碼學在各個領域都起著非常重要的作用。
希爾密碼原理:英文中有26個字母,每個字母對應一個阿拉伯數字,假如向對方傳輸“LOVE”,傳輸者需要先寫出信息對應的數字,即12、15、22、5,然后將這些數字按列寫成兩行的矩陣A,這是原矩陣即信息源,引入加密矩陣C,該矩陣必須為可逆矩陣,B為加密后的矩陣,即對方收到的信息:
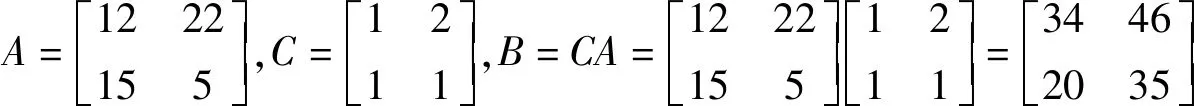
對方接收到的信息即為B矩陣中的四個數字,然后接收者需要解密。操作過程中只需要將接收到的四個數字寫成矩陣B的形式,該部分需要用到逆矩陣的運算進行計算:
對照26個字母對應的數字可以知道源信息為“LOVE”。
以上例子只是簡單介紹原理,所以計算量和加密過程簡單,破解難度小,但是在實際應用中,加密信息的方式更加豐富,信息量要更大,破解的難度也會相應增大,但是可以增加信息傳送的安全性。
2 教學內容的優化
2.1 化繁為簡
課程中有很多定理的證明過程比較復雜,比如克拉默法則在線性方程組的計算中有很大作用,但是其證明過程復雜難懂,可以刪減該部分,著重加強克拉默法則的應用練習。矩陣秩的性質的證明也較為復雜,后期的內容中該部分用處不大,也可省略證明過程等。
2.2 錦上添花
線性代數教學中可以適當增加數學文化與相關歷史人物的內容,重現問題情景以引起學生的情感體驗,提高學生的學習興趣,同時做好線性代數課程思政的融入。
2.3 增加MATLAB,與實際接軌
線性代數教學中經常出現計算冗繁、與現代經濟學科發展脫節的問題,將MATLAB引入教學,能提高學生解決實際問題的能力。比如逆矩陣的計算是矩陣理論中的難點,學生普遍反映其計算過程復雜,有畏難情緒。如果借鑒MATLAB編程,則計算速度很快,操作只需兩步即出答案,大大減少了計算量,同時強化了學生對MATLAB的掌握,提高了學生的應用能力。
3 結語
教學中對線性代數內容進行優化設計能更好地提高學生的學習興趣和學習效率,并能大大提升學生利用知識解決實際問題的能力。

