食品拾放的3-PUU并聯機器人軌跡規劃

郭俊，王新*

1. 內蒙古機電職業技術學院機電工程系（呼和浩特 010070）；2. 內蒙古農業大學職業技術學院車輛工程技術系（包頭 014109）

隨著工業的快速發展，機器人應用越來越廣泛，特別是食品、醫藥等輕工業行業[1-2]，機器人能夠平穩高效地運動離不開有效的軌跡規劃。有效的軌跡規劃使機器人各部件能夠平穩運動，如果各部件之間運動不平穩，各部件之間會存在摩擦和損傷，不僅使機器人的運動性能下降，而且會影響機器人的使用壽命。隨著機器人的不斷發展，對機器人軌跡規劃的探索也在不斷進行。Zhang等[3]以修正正弦運動規律為基礎，在給定路徑下對Delta機器人作了軌跡規劃。Chen等[4]以笛卡爾空間為理論基礎，對Delta機器人進行l軌跡規劃，并得到運動控制算法。梅江平等[5]以B樣條運動規律為基礎對機器人進行軌跡規劃，降低機器人振動，并減少電機功耗。李云輝[6]以修正梯形加速度為理論基礎，對機器人進行軌跡規劃，機器人的運動平穩性明顯提高。因此，主要針對3-PUU并聯機器人在食品拾放高速作業時的運動不平的問題，對機器人的運動軌跡進行軌跡規劃，運用ADAMS和MATLAB聯合仿真的方式，驗證優化后運動軌跡能夠提高機器人的運動平穩性。

1 3-PUU型并聯機器人基本結構

3-PUU并聯機器人主要由動平臺、靜平臺、虎克鉸和3個滑臺鉸鏈組成[7-8]。其結構模型如圖1所示，鉸鏈上裝有驅動滑塊和電動缸，鉸鏈一端固定在靜平臺上，另一端通過虎克鉸與動平臺連接。3個鉸鏈均勻分布于靜平臺上，且與靜平臺呈一固定角度。它具有3個自由度。通過改變滑塊的位置，可以實現末端執行器的運動。

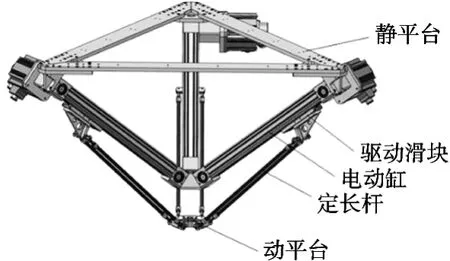
圖1 3-PUU機器人結構模型

2 機器人的軌跡規劃

3-PUU并聯機器人用在食品行業，主要完成拾放動作，而拾放動作的運動軌跡一般采用門字形運動軌跡，門字形運動軌跡的豎直段與水平段之間的連接位置是直角，機器人在此位置時速度和加速度會因運動方向改變而突變，從而產生比較大的慣性力，會使機構產生較大的振動和沖擊[9-10]。因此，需要將直角變為過渡曲線銜接豎直段和水平段，使其平滑過渡；另外，由于并聯機器人高速的拾放動作易引起機構的沖擊和振動，合適的運動規律可以有效減小這種沖擊和振動，所以需要從合適的過渡曲線及合適的運動規律2個方面對機器人的運動軌跡進行規劃，從而保證機器人具有良好的運動性能特性，能夠高速平穩運行。

2.1 機器人運動軌跡設計

一般并聯機器人的門字形軌跡的豎直和水平過渡部分會采用圓弧曲線過渡，一般圓弧與直線軌跡切換時會存在加速度突變，從而會影響機器人的平穩運動，采用回旋線-圓曲線-回旋線的過渡形式，實現加速度的連續變化。其軌跡設計如圖2所示，整個運動軌跡分為9段，并且關于Z軸對稱，AB和IJ為豎直運動段，設，BC和HI為變化率是α12的回旋線，設，CD和HG是半徑為R的圓弧運動段，設，DE和FG是變化率為α22的回旋線，設EF為水平運動，長度為l4。

圖2 運動軌跡設計圖

2.2 機器人運動規律

因為3-PUU并聯機器人在工作過程中具有較高的速度和加速度，所以存在較大的慣性負載和速度負載，為減小運動過程中的沖擊，機器人在運動過程中需滿足2個條件：1）在每段路經的起始點和終止點，末端執行器的速度和加速度都為零；2）在軌跡的中間點，末端執行器的速度和加速度曲線要連續可導。

一般電機的加速度曲線都采用梯形加速度曲線，速度達到較高時，其加速度會具有尖銳突變，所以繼續加速度曲線拐點處需要增加過渡曲線，一般過渡曲線多采用多項式和正弦修正2種方式，這2種方式的效果基本相同，采用正弦修正的方式，修正后的梯形加速度函數如式（1）所示。

式中：T為機器人走完一段運動軌跡所用的時間，單位為s；αmax為運動過程中加速度的最大值，單位為mm/s2。

對式（1）兩邊兩次積分可以得到位移函數。

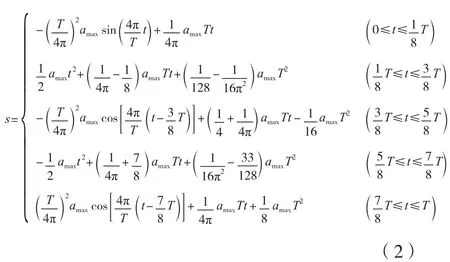
設給定位移為S，允許的最大加速度為αmax，所以機器人的運行周期為式（3）。

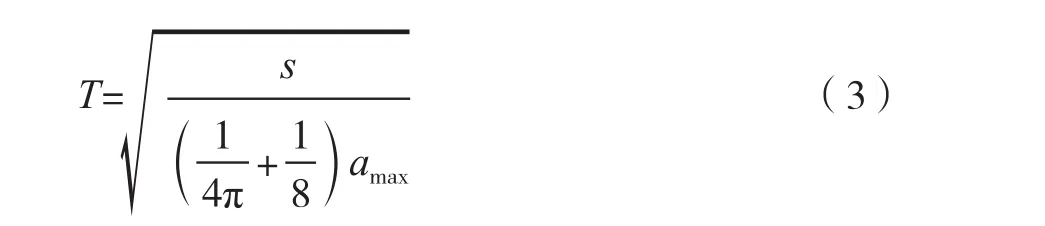
2.3 運動軌跡優化

3-PUU并聯機器人在食品生產線上需要高速拾放目標物，這就要求其運行周期盡量短，所以基于運行周期最短的原則[11-12]，對機器人的門字形運動軌跡參數進行優化。由式（3）可知，要使機器人的運行周期最短，在已知最大允許加速度前提下，需要位移S具有最小值，也就是門字形運動軌跡的路徑最短。由圖2可以得到如式（4）目標函數。

蟻群算法是一種可以用來尋找最優路徑的概率型算法[13]，其具有較強的魯棒性，且較容易收斂，可以較快地得到目標值。其計算流程圖如圖3所示。

圖3 蟻群算法流程圖

以被廣泛認可的美國Adept公司的標準門字形運動軌跡為例，確定算法的數學條件，如式（5）所示。

在MATLAB中采用蟻群算法，按上述數學條件編程，運行得到基于時間最短的個參數數值，為式（6）。

利用此方法，可對不高度和長度的門字形軌跡基于時間最短原則進行優化，并得到各個參數的數值。

根據分析計算，得到機器人優化后的運動軌跡，如圖4所示，它由3段軌跡路徑組成。

各段路徑長度為s1=s3=55.897 mm，s2=219.583 mm。根據修正梯形加速度運動規律得到各段的運動時間，為

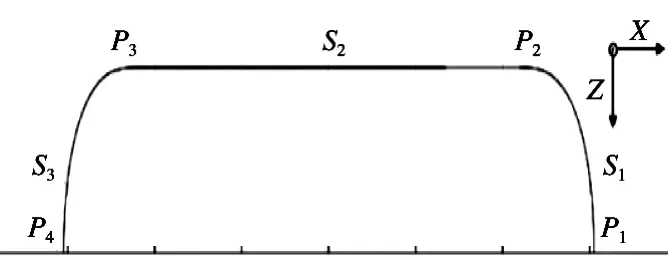
圖4 優化后的門字形軌跡

3 ADAMS和MATLAB聯合仿真

因為在ADAMS中對機械系統進行仿真不需要復雜的推導過程和大量的方程[14-15]，所以可通過ADAMS和MATLAB進行數據交換，將MATLAB中設計的控制系統接入ADAMS中對模型進行控制仿真，得到模型的仿真結果。其具體步驟為：（1）將Solidworks中建立的模型存為通用格式導入ADAMS中；（2）分別以機器人的末端執行器和驅動滑塊的位移、速度、加速度為控制變量，定義仿真的控制輸入和輸出，設定ADAMS和MATLAB的數據通信接口；（3）根據生成的虛擬樣機模型的Simulink模塊搭建仿真平臺，如圖5所示。

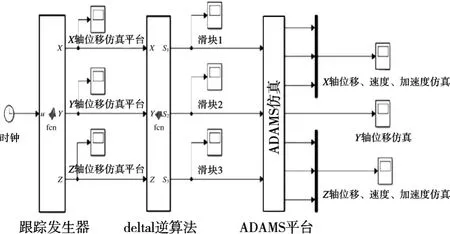
圖5 聯合仿真平臺

分別以軌跡規劃函數和半徑20 mm的圓弧過渡門字形軌跡為仿真模型的輸入，在MATLAB中完成軌跡函數仿真，輸入到ADAMS中完成整個模型的軌跡仿真，通過ADAMS求解器得到軌跡優化后的機器人末端執行器的位移、速度及加速度仿真曲線，如圖6所示。在圓弧過渡軌跡下的機器人末端執行器的位移、速度以及加速度仿真曲線如圖7所示。

對比2種仿真結果可以看出，軌跡優化后機器人末端執行器的位移、速度及加速度曲線變化連續，能夠平滑過渡，無突變，說明機器人運行平穩，無沖擊產生；而圓弧過渡仿真，機器人末端執行器的位移和速度曲線能夠連續變化，且光滑過渡，而加速度曲線雖然也連續變化，但是存在較明顯的突變，且數值波動較大，說明機器人在運動過程存在較明顯的抖動，運動性能不好。可以得到軌跡優化后的機器人運動更加平穩，運動過程中振動較小，說明優化后的門字形運動軌跡能夠提高機器人運動的平穩性，從而可以減小機器人各個部件之間的摩擦和損傷，延長使用壽命。

圖6 軌跡優化后的機器人末端執行器的位移、速度以及加速度仿真曲線

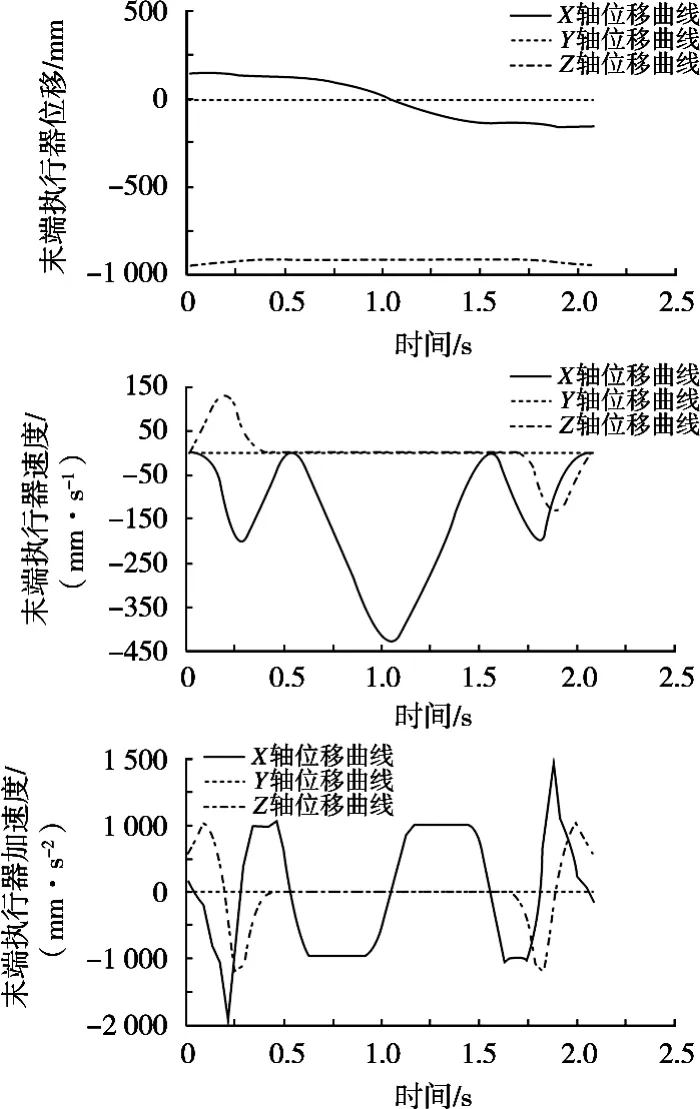
圖7 圓弧過渡軌跡下的機器人末端執行器的位移、速度以及加速度仿真曲線

4 結論

采用回旋線和圓弧線組合的方式作為機器人運動軌跡中2段直線之間的過渡曲線，以修正梯形加速度運動規律為前提，以運動時間最優為目標，采用蟻群算法得到優化后的運動軌跡參數，ADAMS和MATLAB聯合仿真得到優化后和以圓弧過渡曲線2種仿真結果，對比2種結果可得，軌跡優化后的機器人運動更加平穩，運動過程中振動較小。驗證優化后運動軌跡能夠提高機器人的運動平穩性，且會減小機器人各個部件之間的摩擦和損傷，為機器人的運動控制研究提供理論方法及依據。