基于R-ELM算法的火電發電量預測

摘要：R-ELM算法是將極限學習機（ELM）算法和遞歸預測相結合的系統動態建模方法，即對ELM中的隱含層節點數進行遞歸尋優，得到最優隱含層節點數。現建立了一種基于R-ELM算法的火電企業短期日發電量預測模型，該模型根據氣象預報中日最高溫度和日最低溫度，利用過去一段時間的火電實際發電量數據來預測未來4～7天的短期日發電量值。實踐結果顯示，R-ELM算法能快速找到最優隱含層節點數，提高預測精度和泛化能力。

關鍵詞：火電發電量預測;ELM算法;遞歸預測;動態建模

0 ? ?引言

隨著電力行業的發展，風電、光伏等新能源發電占比逐步提升，給火電單位帶來了一定程度的沖擊。新能源發電受天氣因素的影響，具有較強的隨機性，調度往往優先考慮其發電能力，再綜合調配其他形式的發電計劃。但是，調度往往只能給出火電單位近日的發電計劃，對較長時間的發電計劃一般不能及時給出。對火電企業而言，及時掌握未來短期內的發電趨勢，能有效為企業的煤炭短期需求分析提供支持，幫助火電企業制定經營策略[1-2]。目前，火電發電量計劃的主要研究目標是月度電能計劃，計算模式采用平均分配等傳統模式[3-4]，也有基于節能發電調度模式的思路對月度電能計劃進行分解與研究[5-9]。

本文主要研究火電企業未來4～7天的發電量預測趨勢。基于氣象溫度分析，本文建立了一種基于遞歸尋優的極限學習機（Recursive Extreme Learning Machine，R-ELM）算法預測模型。通過日最高溫度和日最低溫度，對原始數據進行ELM預測，并對ELM的隱含層節點數進行遞歸，再通過比較測試結果的精度，得到適用于當前條件的最優隱含層節點數。使用該方法不僅可以快速找到最優隱含層節點數，還能提升預測精度，文章最后以河南省某火電單位的預測結果為例驗證了所提模型的有效性。

1 ? ?R-ELM算法原理

相較于傳統的神經網絡，ELM算法在訓練中能隨機生成輸入層和隱含層之間的連接權重和隱含層神經元的閾值，不需設定大量的參數，只需選擇激活函數并對隱含層神經元的個數進行設置即可獲得全局最優解。ELM算法學習速度快，泛化能力較好，不容易陷入局部最優、過擬合等問題[10-12]，基于這些優點，ELM算法被廣泛應用于非線性函數的擬合、回歸等[13-14]。

給定N個不同的訓練樣本（xj，yj）∈Rn×Rm，激活函數為g（x），且隱含層節點數為L，單隱層前向神經網絡結構模型可用式（1）逼近這N個樣本：

式中：ai為輸入層與隱含層神經元的連接權重;βi為隱含層與輸出層神經元的連接權重;bi為隱含層神經元的閾值。

激活函數可以是“sig” “rbf” “sin”等多種形式。若網絡實際輸出等于期望輸出，則tj=yj，j=1，2，…，N。這N個方程可寫成矩陣形式：

式中：H為N×L維的隱層輸出矩陣，其第i行代表第i個訓練樣本關于所有隱含層節點的輸出，第j列代表所有訓練樣本關于第j個隱含層節點的輸出;β為L×m維矩陣;T為N×m維矩陣。

ELM是一種單隱層前向神經網絡算法，基于上述描述，ELM算法可總結如下：

（1）給定訓練集{（xj，yj）|xj∈Rn，yj∈Rm，j=1，2，…，N}，激活函數為g（x），且隱含層節點數為L，隨機選取輸入權重ai和閾值bi。

（2）計算隱層輸出矩陣H。

（3）計算輸出權重β，全局最優輸出權重可寫為=H*T。H*表示H的Moore-Penrose廣義逆矩陣。

雖然ELM算法優點較多，但是該算法需要人為設定隱含層節點的個數L，L的大小直接影響模型的好壞。過多的隱含層節點數會導致模型擬合過度，從而降低泛化能力，最終影響預測精度[15]。

為了避免人為不斷調整隱含層節點數，減少外界因素對網絡結構的影響，本文提出了一種對ELM的參數L不斷進行優化的遞歸方法，并建立了R-ELM動態發電量預測模型。R-ELM模型的計算流程如圖1所示。

詳細預測步驟如下：

（1）準備數值，包括天氣預報提供的日最高溫度、日最低溫度、訓練數據、測試數據。

（2）訓練數據和測試數據歸一化。

（3）確定神經網絡的拓撲結構，初始化ELM網絡的權重和閾值編碼，設定初始隱含層節點數為L1=1，L2=7，L3=13。

（4）依次根據L1，L2，L3的值分別對ELM網絡進行訓練，并得到3組反歸一化后的測試結果。

（5）計算（4）中測試結果的適應度值，分別設為F1，F2，F3，并比較三者的大小關系。

如果F1最小，則L3=L2，并且L2=（L1+L3）/2的下整數;

如果F3最小，則L1=L2，并且L2=（L1+L3）/2的下整數;

如果F2最小，則L1=（L1+L2）/2的下整數，并且L3=（L2+L3）/2

的下整數。

（6）進入（4）～（5）遞歸迭代，直到max（F1，F2，F3）-

min（F1，F2，F3）<0.01時停止遞歸。將此時min（F1，F2，F3）對應的隱含層節點數作為最優參數。

（7）用最優隱含層節點數對應的ELM網絡結構作為當前模型，輸入預測的未來4～7天的氣象數據得到預測結果。

2 ? ?基于R-ELM算法的火電發電量仿真預測

2.1 ? ?模型輸入變量分析

是否選擇了正確的輸入變量和訓練數據，將直接影響模型訓練的預測效果。因此，需要對輸入變量和訓練數據加以分析選擇。

本文對數值天氣預報（Numerical Weather Prediction，NWP）預測的未來4～7天的日最高溫度、日最低溫度、日均風速、天氣狀況（晴、多云、雨或雪）和火電廠實際發電量進行了分析。為了定量評價這些氣象因素與實測數據的強弱關聯性關系，引入了相關系數：

式中：X和Y為兩個向量數組;Cov（X，Y）為X和Y之間的協方差;σX和σY為X和Y的方差。

本文以河南某火電廠為例分析氣象數據與實測數據的關系。利用式（3）計算2019年第1季度至2020年第2季度氣象數據與實際發電量的相關系數，結果如表1所示。可以看出，日最高溫度、日最低溫度與實際發電量的相關系數的絕對值相對較大，日均風速、天氣狀況的相關系數的絕對值相對較小。因此，本文根據相關性選擇日最高溫度、日最低溫度作為ELM的輸入變量。

2.2 ? ?訓練數據分析

以上述火電廠的數據為例繼續分析模型訓練數據。由于火電廠的發電量跟溫度的相關系數較高，因此選擇分析2020年和2019年同時期的實際發電量數據。經過數據分析，2020年和2019年同時期的實際發電量值與日最低溫度的關系趨勢基本一致。

由于訓練數據過多或過少都會直接影響模型效果，因此，本文訓練樣本的選擇規則為每天的前15天數據加上2019年同期前后各15天的數據，并選擇最近5天的數據作為測試樣本。

2.3 ? ?仿真結果

為了統計預測誤差，本文采用標準均方根誤差（Normalized Root Mean Square Error，NRMSE）作為適應度函數進行誤差分析，計算公式如下：

式中：Realpi為輸出層第i個預測點的預測值;Forepi為輸出層第i個預測點的實際值;n為預測點的個數;Maxp為電廠的機組總容量。

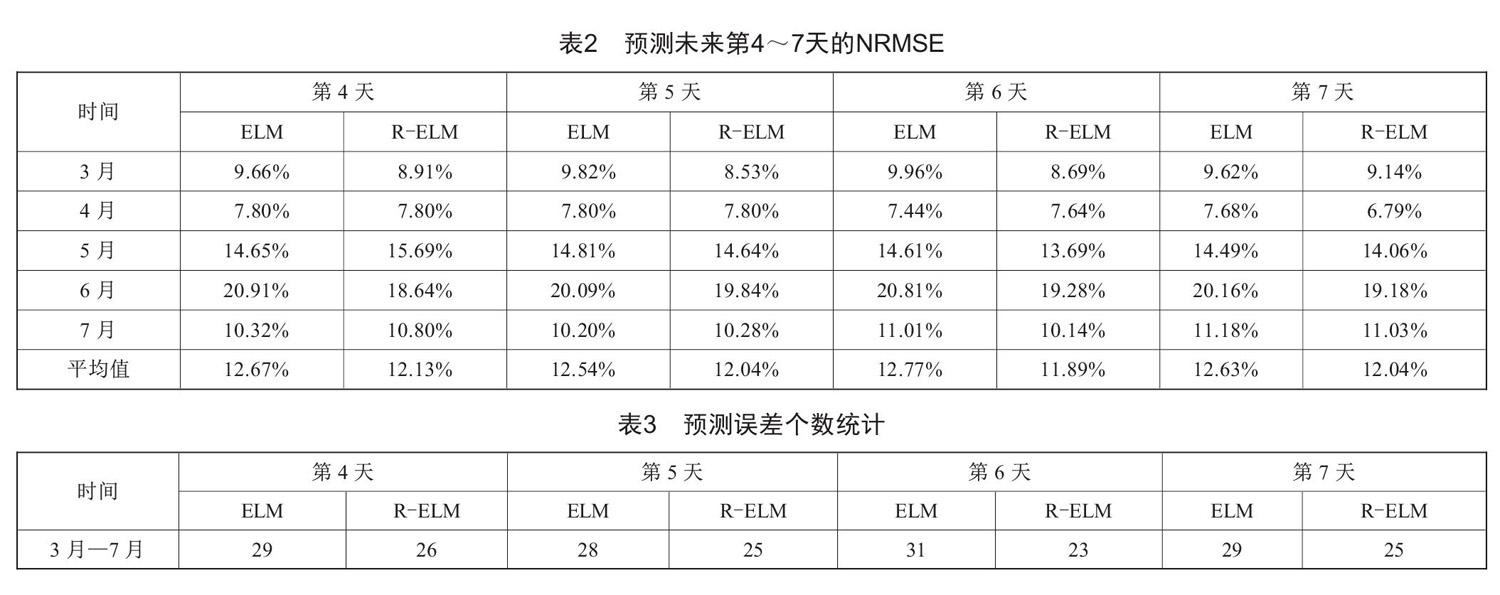
輸入NWP提供的日均最高溫度、日均最低溫度，對火電廠未來4～7天的發電量進行預測，預測方法分別采用固定隱含層節點數為5的ELM算法和R-ELM算法，預測結果的標準均方根誤差如表2所示。從表2可以看出，R-ELM的預測效果明顯優于ELM，說明經過遞歸尋優確定最優隱含層節點數的方法精度更高。

為了進一步驗證本文方法的泛化性能，表3列出了兩種預測實驗中相對誤差大于20%的誤差點的個數。由表3可以看出，R-ELM模型的預測誤差大于20%的點個數均少于ELM模型。這表明發電量波動較大時，R-ELM模型能夠獲得相對較小的誤差，具有較好的泛化能力。

3 ? ?結語

本文基于數值天氣預報數據，通過分析氣象數據和歷史數據趨勢，選擇模型的訓練數據，并對ELM算法的隱含層節點數進行遞歸尋優。根據預測結果可以得出以下結論：

（1）R-ELM算法能快速尋優最佳隱含層節點數。

（2）從預測標準均方根誤差來看，R-ELM算法的預測結果比相應的ELM預測精度高。

（3）R-ELM算法的預測模型具有良好的泛化性能，因此，除了應用于火電單位發電量預測領域外，還可以應用于其他領域的預測模型。

[參考文獻]

[1] 馬姍姍.發電企業燃煤庫存管理優化研究[D].北京：華北電力大學，2014.

[2] 解超.電力行業煤炭需求分析及預測[D].北京：華北電力大學，2015.

[3] 毛毅，車文妍.兼顧節能與經濟效益的月度發電計劃模型[J].現代電力，2008，25（5）：73-78.

[4] 范玉宏，張維，韓文長，等.區域電網節能發電調度模式研究[J].電力系統保護與控制，2009，37（16）：107-111.

[5] 張森林.節能發電調度配套上網電價定價機制研究[J].電網技術，2009，33（18）：105-110.

[6] 湯偉，王漪，于繼來，等.編制直調火力發電單元月度電能交易計劃的綜合耗量優化法[J].中國電機工程學報，2009，29（25）：64-70.

[7] 湯偉，王漪，于峰，等.編制直調火力發電單元月度電能交易計劃的綜合成本加權法[J].電網技術，2009，33（17）：167-173.

[8] 王漪，湯偉，羅桓桓，等.編制直調火力發電單元月度電能交易計劃的負荷率偏差法[J].電力系統保護與控制，2009，37（22）：134-140.

[9] 張慧琦，常永吉，唐大勇，等.節能發電調度模式下火力發電單元的月度電能計劃編制方法[J].電力系統保護與控制，2011，39（4）：84-89.

[10] LAN Y，SOH Y C，HUANG G B.Ensemble of online sequential extreme learning machine[J].Neuro-

computing，2009，72（13/14/15）：3391-3395.

[11] HUANG G B，DING X J，ZHOU H M.Optimization method based extreme learning machine for classific-ation[J].Neurocomputing，2010，74（1/2/3）：155-163.

[12] WANG Y G，CAO F L，YUAN Y B.A study on effectiv-eness of extreme learning machine[J].Neurocom-puting，2011，74（16）：2483-2490.

[13] 程琳，趙文杰.基于GA-ELM的SCR脫硝系統動態建模[J].熱力發電，2019，48（6）：29-33.

[14] 路小娟，朱正平.基于ELM的風力發電量的預測研究[J].自動化與儀器儀表，2015（11）：159-161.

[15] LI M Y，ZHANG X.A modified more rapid sequential extreme learning machine[C]// 2016 8th Interna-tional Conference on Computational Intelligence and Communication Networks （CICN），2016：336-340.

收稿日期：2020-11-26

作者簡介：卞彩鳳（1983—），女，山東萊陽人，碩士研究生，研究方向：人工智能算法、大數據可視化等。