電子地圖軌道地理坐標描述方法研究
陳志強,鮑鵬宇
(1.北京全路通信信號研究設計院集團有限公司,北京 100070;2.北京市高速鐵路運行控制系統工程技術研究中心,北京 100070)
列控系統車載設備測速測距傳感器無法消除距離的累積誤差,需要在地面鋪設大量應答器設備進行位置校準,這增加了地面設備維護工作量[1-3]。由于衛星定位系統進行列車定位時無累計誤差,可替代應答器設備實現列車位置校準[4-6]。2020 年6 月23 日北斗三號最后一個組網衛星發射成功,北斗三號全球衛星導航系統星座部署已全面完成,這給衛星定位系統在鐵路列車控制領域的應用打下了基礎和機遇。然而由于衛星定位提供的是經緯度二維坐標,而列控系統使用的是一維的軌道相對位置,為將二維的衛星坐標映射到一維的軌道上,需要提供軌道的坐標電子地圖數據。本文基于此問題,對軌道電子地圖的生成方法展開研討。
1 軌道近似描述方法
鐵路軌道可使用直軌和彎軌進行近似描述[7-8],其中直軌可用直線段上的點進行描述,而彎軌包含兩種描述方法:曲線描述法和線段近似法。
1)曲率描述法
曲率描述法即直接使用包含曲率半徑R 和角度α 的曲線描述一段彎軌,如圖1(a)所示。
2)線段近似法
線段近似法即在彎軌上選擇若干個近似點,連接近似點形成若干個近似線段,使用若干個線段近似描述一段彎軌,如圖1(b)所示。
比較曲率描述和線段近似兩種方法:
1)參數比較:曲率描述法使用R 和α 兩個參數即可描述一段彎軌,運算參數較少。而線段近似法需要包含若干個分段點的經緯度坐標,參數較多;
2)算法復雜度比較:二維衛星定位點向一維軌道投影時,曲率描述法需要大量使用三角函數運算,算法復雜。線段近似法直接進行線性運算,算法簡單;
3) 工程難度比較:曲率描述法的R 和α 工程測量困難,而線段近似法的分段點工程測量簡單。

圖1 軌道描述方法Fig.1 Track description method
綜上所述,線段近似法雖然數據量稍大,但算法簡單和工程測量難度小,具有更好的可行性。
2 線段近似方法
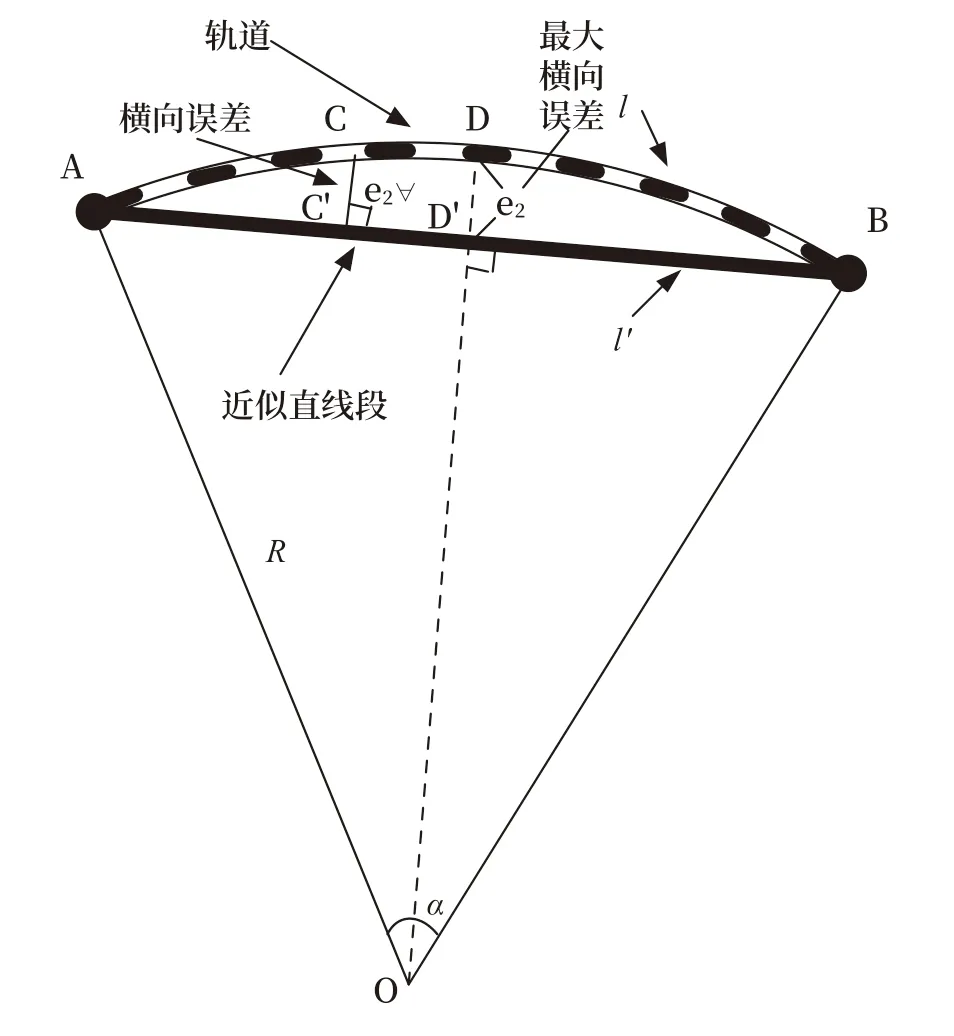
圖2 線段近似算法Fig.2 Line segment approximation algorithms
1) 縱向誤差和最大縱向誤差

其中,

將公式(2)和(3)代入公式(1)有

將公式(4)進行化簡,有
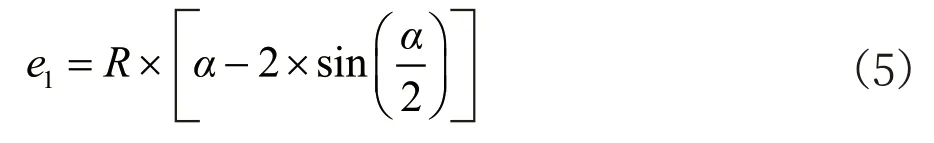
2)最大橫向誤差
點C 的橫向誤差為CC′。

其中,

將公式(7)和(8)代入公式(6)有

將公式(9)進行化簡,有

由公式(2)可知

將公式(11)分別代入公式(5)和(10),可以得到誤差和運行距離l 及曲率半徑R 的關系
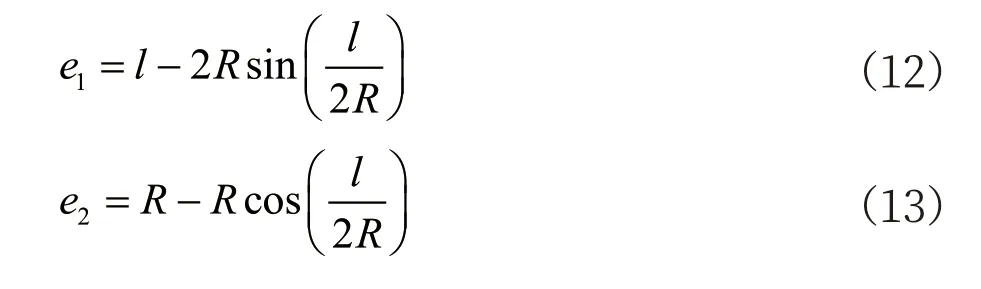
3 誤差控制方法
由于實地測量的軌道衛星坐標誤差需控制在固定范圍(設為emax)內。由公式(12)和(13)可知,當曲率半徑固定時,誤差只與運行距離l 相關,對公式(12)和(13)中的l 求導,可得到
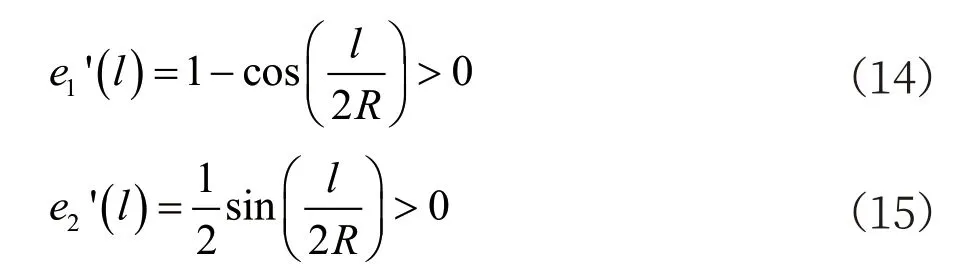
由公式(14)和(15)可知,當曲率半徑固定時,隨著l 的增大,誤差e1和e2逐漸增大。因此使用線段AB 近似圓弧時,若誤差超過emax,可通過在AB 間增加若干個近似點的方法縮短距離l,進而減小誤差。
定理1:當運行弧長l ∈[0,2Rarctan(0.5)]時,橫向誤差大于等于縱向誤差。
證明:
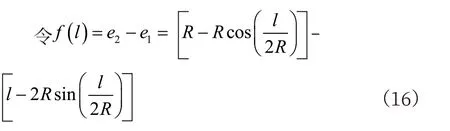
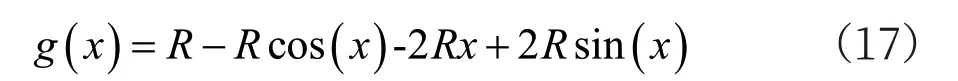
x=0 時有g(0)=0,將g(x)對x 求導,有
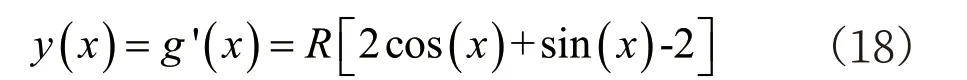
x=0 時有y(0)=0,將y(x)對x 求導,有
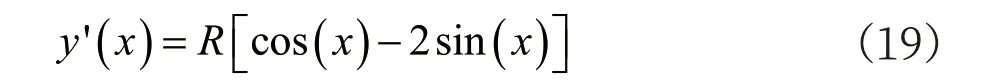
易知,當x ∈[0,arctan(0.5)]時,有y′(x)≥0,即y(x)在[0,arctan(0.5)]內是增函數。由于y(0)=0,有x ∈[0,arctan(0.5)]時,y(x)≥0。
同理,有x ∈[0,arctan(0.5)]時,g(x)≥0,即e2≥e1。
由于l=2Rx,有l ∈[0,2Rarctan(0.5)]時,e2≥e1。
證畢。
根據定理1 可知,當l <2Rarctan(0.5)時,橫向誤差大于縱向誤差,因此在此范圍內可使用公式(20)計算最大誤差e 時的弧長l 值。

可將工程允許的最大誤差帶入公式(20)中,即可獲得最大圓弧長度用以限定近似點間隔。
4 仿真計算
根據應用公式(13)和定理1,可得到各曲率半徑下弧線長度l 和最大誤差之間的關系,以及弧線長度l 滿足定理1 的最大值lmax,如表1 所示。

表1 弧線長度和最大誤差的關系Tab.1 Relationship between arc length and maximum error m
根據表1 可生成弧長誤差關系曲線,如圖3 所示。如表1 和圖3 所示,若曲率半徑不小于300 m,則軌道的采樣間隔弧長最小為50 m 即可滿足1 m的精度要求;軌道采樣間隔弧長最小為20 m 即可滿足0.2 m 的精度要求。且隨著曲率半徑的增加或最小誤差的增加,采樣間隔弧長逐漸增加。

圖3 弧線長度和最大誤差的關系曲線Fig.3 Relation curve between arc length and maximum error
5 結論
本論文首先對電子地圖中彎軌的曲線描述法和線段近似法兩種方法的優缺點進行分析,得出線段近似法更易于應用和實施的結論,然后對線段近似法的誤差進行分析,提出線段近似法中近似點間隔的確定方法。該方法既可以滿足地圖描述精度要求,又能最大程度上降低電子地圖的數據量。本論文提出的電子地圖描述方法,為衛星定位系統在列控系統中的有效應用提供了切實可行的方法和理論支撐。

