雙質體振動系統的周期運動與分岔特性

南向曈 鄒燁

（湖南鐵道職業技術學院 湖南省株洲市 412001）

含間隙和約束的機械設備在工作時會產生機械振動，引發機構不同部件之間及設備與地面、墻面之間發生機械碰撞，從而導致設備零部件的磨損及噪音的產生，影響設備運行可靠性及使用壽命。因此，對碰撞振動問題的研究存在重要應用價值，雙質體沖擊振動成型機就是一類典型的碰撞振動設備，對其振動問題的研究具有一定的代表性。目前多采用系統動力學方法，將機械設備簡化為含間隙的振動系統動力學模型，進而研究其碰撞振動特性，進行動力學優化設計。沖擊振動系統的非線性動力學研究對于具有沖擊振動和運動限制約束的機械系統動力學性能優化和噪聲抑制的匹配設計具有實際意義[1]。近幾年各學者在相關方向持續作了深入研究[2-3]，侍玉青等用雙參圖呈現研究數據，分析含間隙振動系統低頻周期沖擊振動的模式類型及分岔特征[4]；張曉蓉等研究了兩自由度赫茲接觸碰撞振動系統在低頻率、小間隙下存在的非完全顫振、遲滯區域共存等現象，得出高頻下對稱周期運動轉遷到非對稱的周期運動的變化規律[5]。

1 力學模型

將Hertz 接觸理論與雙質體沖擊振動成型機的傳統模型相結合，將振動系統兩質體間的碰撞處理為彈性碰撞，并考慮碰撞面間的等效阻尼，以Kh表示兩質體碰撞面間的剛度，Ch表示兩質塊碰撞面間的阻尼，得到該振動系統的簡化非線性動力學模型如圖1所示。

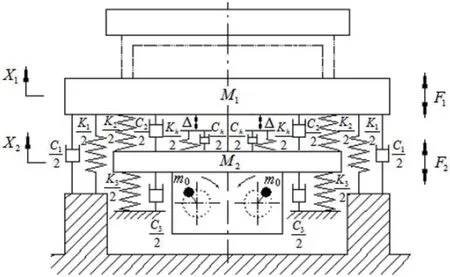
圖1：雙質體沖擊振動成型機的彈性碰撞模型

圖中其他參數的含義如表1所示，兩質體間的碰撞條件為X2-X1=Δ。

表1：碰撞模型中各參數含義

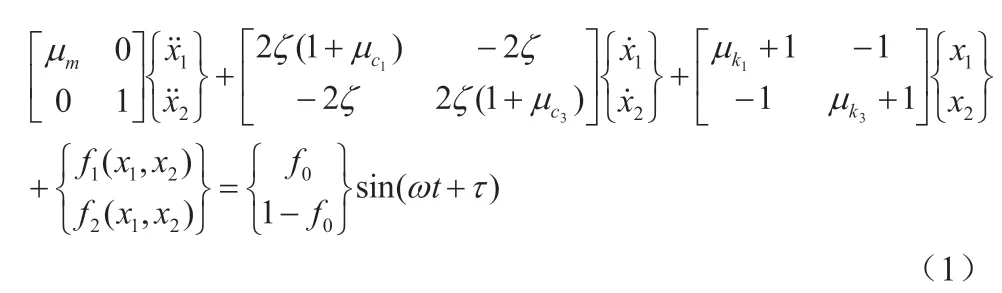
其中f(x1,x2)為兩碰撞面間Hertz 接觸力[6]的無量綱化形式，其具體表達式如（2）式所示。

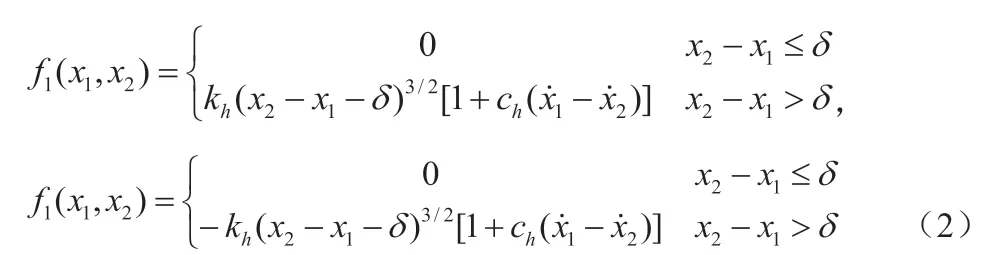
引入碰撞恢復系數R，由碰撞理論和動量守恒定律，兩質體碰撞前、后的瞬時速度和滿足：

2 Poincaré映射及分岔特性

取（5）式所示Poincaré 截面，并建立相應周期運動的Poincaré映射如（6）式所示。

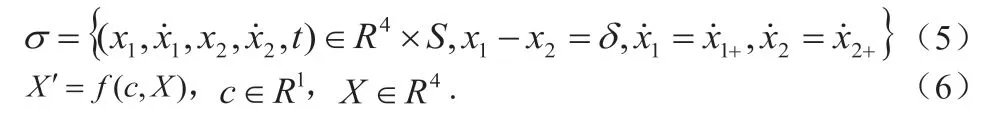
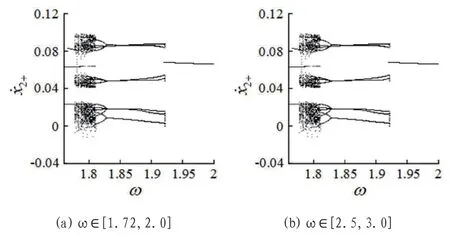
圖2：局部分岔圖

隨激振頻率ω 的增大，系統在ω∈[1.72,2.0]頻域內由周期2 運動狀態經歷瞬間激變進入混沌狀態，其后經歷逆周期倍化分岔逐漸轉遷到多周期運動狀態，再經歷瞬間激變進入穩定的周期1 運動狀態，如圖2(a)所示；在ω∈[2.5,3.0]頻域內系統的運動特性類似，也是先處于混沌狀態，而后經由Feigenbaum 逆倍周期序列由長周期多沖擊運動狀態逐步過渡到周期1 運動狀態，其間依次經歷概周期-周期8-周期4-周期2-周期1 等典型運動狀態，如圖2(b)所示。

借助相平面圖觀察激振頻率ω=2.9 時系統的瞬時運動特性，對比兩質體在這一碰撞瞬間的振動模式，如圖3所示。可見質體M1的相圖為一條封閉曲線，即處于周期1 運動模式，由右側豎線可知質體M1在位移接近0.004 位置與質體M2發生碰撞，如圖3(a)所示；此時質體M2的位移接近-0.02，且其碰撞后未直接進入下一運動周期，而是又經歷了一次未發生碰撞的小幅振動，運動特性比質體M1豐富，如圖3(b)所示。其對應速度隨時間的響應圖如圖4，顯然質體M1在相鄰兩次碰撞間只經歷一次振動，從平衡位置一側運動到平衡位置的過程中速度逐漸降到0，其后速度反向增大并向平衡位置另一側運動，達到最大距離后返回，完成一次完整的振動，如圖4(a)所示；質體M2則在對應兩次碰撞間發生兩次幅值不同的振動，如圖4(b)所示，與圖3分析結果相對應。

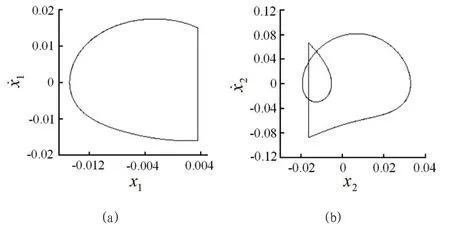
圖3：ω=2.9 時兩質體的相平面圖

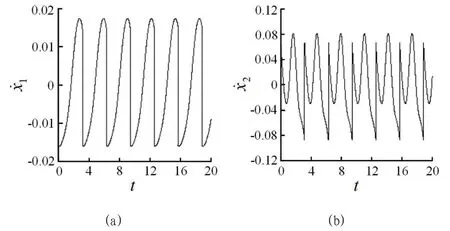
圖4：ω=2.9 時兩質體的時間歷程圖

圖5所示為質體M2在不同外激勵頻率下的Poincaré 截面投影映射圖，呈現出典型的混沌吸引子，可見此時系統處于混沌狀態，兩質體的碰撞振動特性無明顯規律性。但隨激振頻率增大，混沌吸引子由圖5(a)所示的整體聚集狀態逐步過渡到圖5(c)所示的三塊聚集狀態，預示系統由混沌運動向多周期運動的演化過程，與圖2分岔特性相對應。

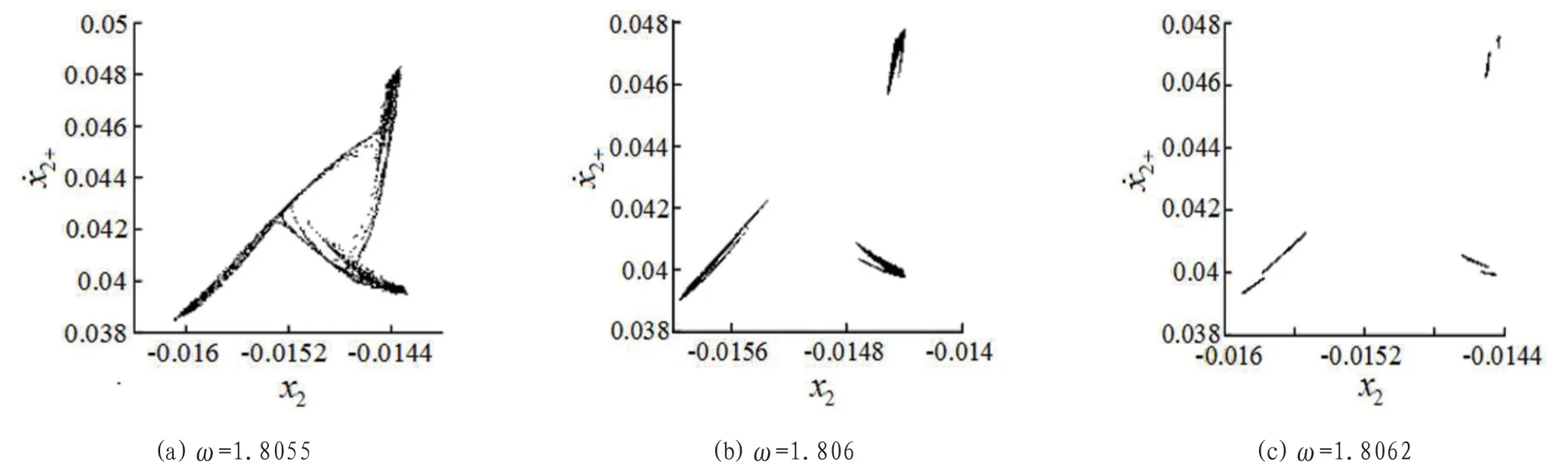
圖5：混沌狀態下的Poincaré 截面圖

3 結論

文章對雙質體沖擊振動成型機的傳統模型進行改進，引入Hertz 接觸理論，將系統兩質體間的碰撞關系處理為彈性碰撞，并同時考慮碰撞面間的等效剛度和阻尼對碰撞特性的影響。在所選基準參數下，揭示了系統在所選Poincaré 截面下的周期沖擊振動模式及相應分岔特性。研究顯示，系統在外激勵頻率ω＜3.0 頻域內表現出復雜多樣的非線性動力學特性，在混沌、瞬間激變、倍化分岔及其他多周期等振動模式之間相互轉變，平穩的周期1 運動窗口很窄，兩質體的振動模式均不穩定。