基于改進模擬退火算法的社會力量救災派遣模型*

李 瑩，李 忠，張莉麗

(1.防災科技學院 應急管理學院,河北 廊坊 065201； 2.防災科技學院 地球科學學院,河北 廊坊 065201)

0 引言

巨大災害的發生往往可能造成極大的人員傷亡和財產損失。但由于受災區域自然環境、地質條件、人文生態等因素影響，導致政府救援工作出現人力短缺、救助不及時等問題[1]。隨著我國經濟的發展和社會的進步，越來越多的社會力量參與到災后的救援工作中[2]。據統計,汶川地震發生后，中國紅十字會征集志愿者18萬人，四川各級團委登記的志愿者達到118.5萬人,共向災區派出志愿者150.85萬人次[2]。但社會力量人員數量、技術能力、財物狀況、位置信息等均未知，往往造成救援的無信息、無秩序、無調度、無管理的“四無”混亂狀態，有時甚至“幫倒忙”。不同的災害需要不同的救援技能，如在洪水災害救援中，需要具備游水、高空繩索救援和操作皮劃艇等能力。所以需要根據受災情況派遣具備相應能力的社會組織，以達到救援效率最高和救援效益最大。

針對災后救援中存在的問題，我國學者進行大量研究。其中1個重要課題是如何合理地調配救援力量，這是提高救援效率、減少人員傷亡的重要途徑[3]。科學地分析災區救援力量的需求，并合理地派遣隊伍，才能以最少的救援資源達到最大程度的救援效果[4]。目前，國內外學者對此進行大量研究：Friedrich等[5]開發決策支持系統用于營救地震災后幸存者，在該系統中可以根據災情設計最佳搜救路線；Mike等[6]根據 Arcgis 中的路徑成本矩陣分析功能，設計火災救援調度的最優化方案；袁媛等[7]以救援任務勝任程度和時間滿意度為目標函數建立模型，將雙目標模型轉化為單目標模型，并用匈牙利法求解得出最優派遣方案；梵治平等[8]針對突發事件應急救援人員分組問題，以救援效果為目標，構建救援人員分組模型；張雷等[9]根據災后的需求分析，采用基于優化模型的分組算法來解決地震災害應急救援隊伍的分組問題；Sampson等[10]根據參與救援人員的意向建立模型從而求解人員派遣問題；張淑文等[11]提出災情優先、距離優先、兼顧災情和距離3種調度策略，并采用非支配遺傳算法對模型進行求解得到最優派遣策略；李亦綱等[12]基于資源優化分配模型和算法，從救災對象的分級、救援需求分析和基于運輸問題的救援力量優化調配求解方面對地震災區救援力量優化調配模型進行較全面的研究，給出相對完整的技術思路和初步的應用，以此來提高救援效率；李懷明等[13]以整體救援效果最佳為目標，以綜合救援效益為目標函數建立救援人員分組模型，雖然該模型可以得出比較合理的派遣方案，但其未考慮經濟成本這一因素。雖然上述方案可以求解出災后救援派遣方案，但其均以專業救援隊為對象建立模型，不適合社會力量此類救災群體的情況。

所謂的社會力量是指能夠參與并作用于社會發展的社會組成部分，包括非政府組織、志愿者、企業等。汶川地震以后，我國越來越多的社會力量參與災后救援行動，大大提高救援效率。如汶川地震發生之后，各類社會組織和廣大志愿者火速趕往災區參與救援[14]。在“8·8”九寨溝地震救援中社會力量也起到積極的作用[15]。社會力量在參與災后救援中有較多優勢，主要包括多渠道籌集社會資源、及時了解各類求助群體的需求和提供更加專業化的救助等[16]。但也存在一些問題，包括貿然進入災區導致交通擁堵、救援行動缺乏協同性等。隨著我國社會力量的不斷發展，為健全社會力量參與災后救援的工作機制，促進社會力量高效有序地參與災后救援工作，2017年12月28日，民政部發布《社會力量參與一線救災行動指南》，指出社會力量在災后救援中應本著“量力而行、就近就便”的原則，根據災區需求和自身擅長的領域來開展救災工作[17]。本文針對社會力量這一救災群體，對災后救援派遣模型展開研究，以提高社會力量參與災后救援的效率。

對于救援隊分配模型問題，目前我國學者已經進行大量的研究，但社會力量與專業救援隊有所不同，他們分散各地，面向不一，其掌握的救援技能也各不相同[18]。鑒于此，本文針對災后社會力量救援派遣問題，綜合考慮救援效益、時間成本和經濟成本3個因素建立模型，并采用改進的模擬退火算法對模型進行求解，得出最優派遣策略。

1 問題描述及數學建模

社會力量組織參加災后救援是1個復雜的社會問題，涉及到裝備、技能、位置、時間、人力、財政、交通等問題，需要進行細心規劃和調度，以使得救援效益最大化。

1.1 問題描述

假設有若干個受災地區需要救助，有多個社會力量組織參與救助工作，但每個社會組織具有的救援技能不同、所在的位置不同、到達災區的時間不同、能夠接受的最大救援成本不同，根據上述情況求解最優救援派遣方案。

這是1個多參數的社會組織救災效益最大化的求解問題，可以通過建立數學模型進行求解。

社會力量參與災后救援模型的建立與求解示意如圖1所示。本文所需求解的問題是：在得知各社會力量救援能力和災區情況的條件下，結合實際情況調整約束條件，根據不同的災區救援需求計算最佳派遣方案，使得綜合救援效益最大。

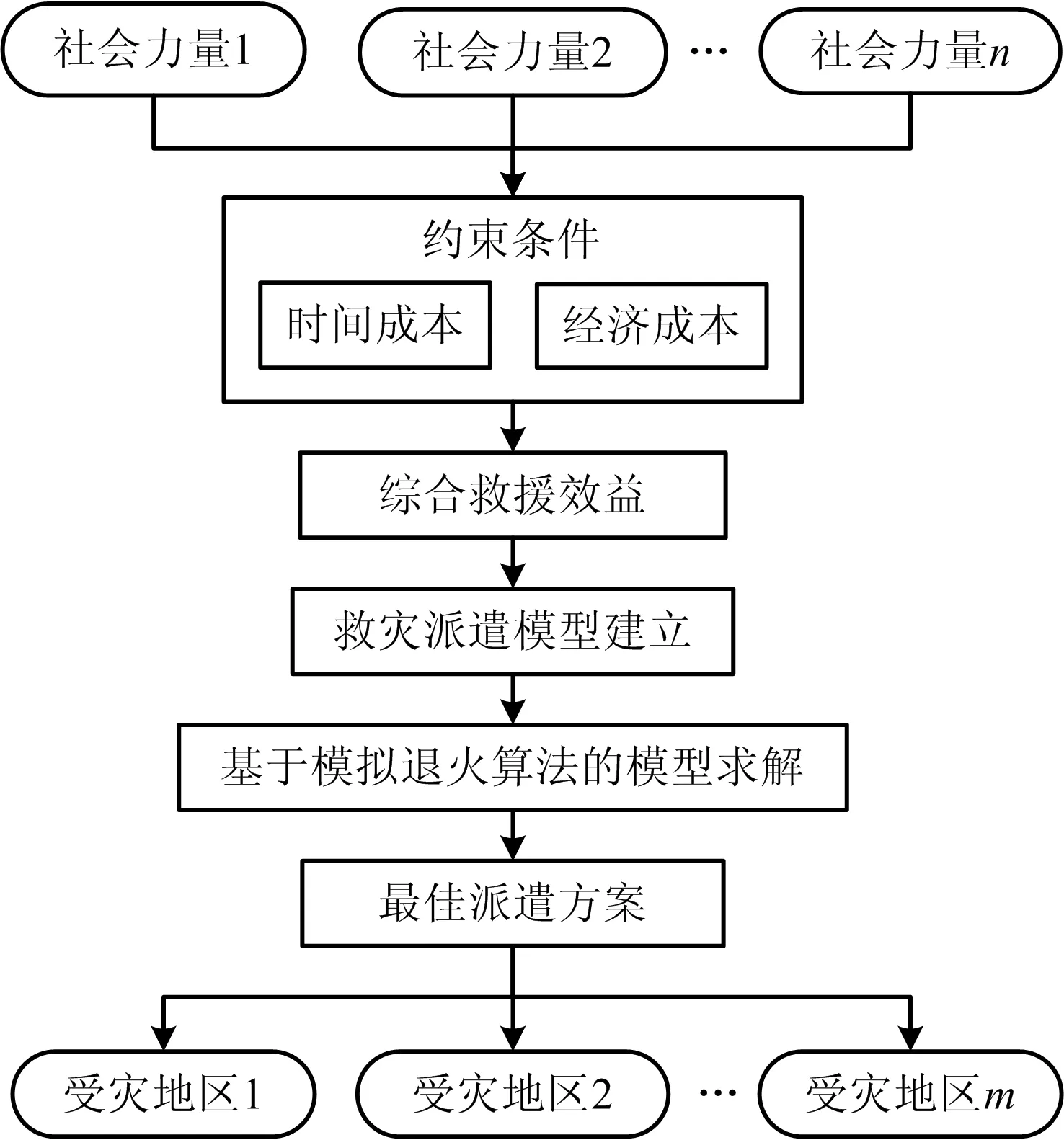
圖1 社會力量救災派遣模型的建立與求解示意Fig.1 Schematic diagram for establishing and solving dispatch model of social forces for disaster relief

1.2 假設條件

考慮到建立多參數優化問題數學模型的復雜性，為便于研究和求解，需要進行如下合理的假設：

1)在對社會力量評估后允許其進入災區實施救援。

2)各社會力量到達災區的時間可以估算。

3)各社會力量前往各地的經濟成本可被估算。

4)各個受災地的受災情況可被估計。

1.3 符號說明

由社會力量組成的救援組織(以下簡稱社會組織)參與災后救援派遣模型中相關的數學量符號含義如下：

D={D1,D2,D3,…,Dm}表示災區Di組成的集合。

M={M1,M2,M3…,Mn}表示社會組織Mj組成的集合。

P={P1,P2,P3,…,Pl}表示本次救援所需技能種類Pk組成的集合。

T={tij|i=1,2,3,…,m,j=1,2,3,…,n}表示社會組織Mj抵達災區Di所花費的時間tij組成的集合。

F={fi|i=1,2,3,…,m}表示災區Di的最佳救援時間fi組成的集合。

G={gij|i=1,2,3,…,m,j=1,2,3,…,n}表示不同社會組織前往不同災區的救援經濟成本gij組成的集合。

H={hj|j=1,2,3,…,n}表示社會組織Mj的救援預算成本hj組成的集合，萬元。

B={bik|i=1,2,3,…,m,k=1,2,3,…,l}表示災區Di對救援技能Pk的需求程度bik組成的集合，分為高、中、低3個等級，分別用Ⅲ，Ⅱ，Ⅰ表示。

R={rjk|j=1,2,3,…,n,k=1,2,3,…,l}表示社會組織Mj擁有救援技能Pk的等級rjk組成的集合，每種技能可分為高、中、低3個等級，分別用3，2，1表示。

S={si|i=1,2,3,…,m}表示災區Di對社會組織的最大需求量si組成的集合。

X={xij|i=1,2,3,…,m,j=1,2,3,…n}表示社會組織Mj是否前往受災地Di進行援助標識xij∈{0,1}組成的集合，等于1時為前往，0為不去，根據集合結果確定分配方案。

1.4 救援匹配度

每個社會組織掌握的技能各不相同，技能水平等級有高低之分。因此，根據災區災情，對每個社會組織救援掌握的技能等級與災區需求的救援技能情況進行匹配度計算，幫助社會組織匹配到最合適的災區，提高救援效率。故救援效益最大化問題轉化為最佳匹配度問題。

每個社會組織的救援技能以及等級評估，按照3級原則在日常的管理中可以完成；災害發生后，不同災區對救援技能以及等級需求、最佳救援時間等信息可以在災情發生后通過快速評估獲得。則災區需要的救援技能及等級與社會組織的救援技能及等級的匹配度eij計算如式(1)所示：

(1)

式中：eij為社會組織Mj對災區Di的匹配度，值域為[0,1]，數值越接近1，表示匹配越好，越接近0，表示匹配越差。

如某災區對救援技能需求為城市搜救能力、高空繩索能力、山地救援能力、水上救援、醫療救助能力、后勤保障能力6種救援技能，需求程度等級對應為[Ⅲ，Ⅲ，Ⅱ，Ⅱ，Ⅲ，Ⅱ]；而某組織的救援技能對應等級為[3,2,2,1,1,1]。利用式(1)計算得到該社會組織對應于災區的技能匹配度為0.82，說明該社會組織較適合前往此災區進行救援，再結合抵達災區時間和經濟成本考慮是否派遣至災區。

1.5 模型及約束條件

設目標函數為救援效益最大，即所有災區需求技能與社會組織掌握技能的總體匹配度最高，如式(2)所示：

(2)

式中：E表示綜合救援效益；xij表示社會組織Mj是否前往受災地Di進行援助。

另外需要考慮經濟成本和時間因素。前往災區的經濟成本需要根據交通工具、生活成本以及其他救援成本計算總的經濟成本，使之不超過社會組織的救援預算總額；時間成本可以根據社會組織所在位置到災區的距離以及可用的交通工具進行估算，救援組織抵達災區的時間應不超過災區最佳救援時間。約束條件如式(3)～(7)所示：

(3)

(4)

(5)

(6)

(7)

式(3)表示經濟約束；式(4)表示時間約束；式(5)表示救援技能匹配度達到0.5以上才可考慮是否將其派遣到相應災區；式(6)表示每個救援組織只能前往1個災區實施救援；式(7)表示派往某災區的社會組織數量不可超過該災區需求的最大組織數量，災區最大救援需求量由災區的地區系數、季節系數、事故發生時間、受災嚴重程度等確定。

2 基于改進的模擬退火算法的模型求解

模擬退火算法是模擬固體冷卻的原理而設計的1種優化算法，從某一較高的溫度開始，隨著時間的變化，溫度不斷地下降，直至達到與環境溫度一致，此時內能減至最小[19]。算法改進如下：

1)初始解的選擇

初始解為隨機生成m×n維0，1矩陣，表示社會組織Mj前往災區Di。在生成過程中，需要考慮式(7)的約束條件，即派遣到災區的社會組織數量不得超過該災區需求的最大組織量。

2)目標函數及約束條件

目標函數為總救援效益最大，同時，以經濟成本和抵達災區的時間作為約束條件。

3)選擇新解

在初始的分配方案上隨機選擇1個社會組織的救援地進行更換。

4)目標函數差

計算變換前與變換后目標函數的差值ΔE，如式(8)所示：

ΔE=E′-E

(8)

式中：E′表示新解；E表示舊解。

5)Metropolis接受準則

Metropolis接受準則是1個重要性采樣函數，接受準則如公式(9)所示：

(9)

式中：P表示接受新解的概率；t表示迭代次數。

在Metropolis接受準則的基礎上，新方案還需滿足式(3)～(7)的約束條件。如果有1個約束條件不滿足，則P=0。

6)退火策略

為提高找到全局最優解的概率，使用基于牛頓冷卻定律的溫度衰減函數來實現。牛頓冷卻定律是在考慮周圍環境溫度固定的條件下，計算1個熱物體溫度隨時間變化的規律[20]，其表達式如式(10)所示：

T(t)=Tc+(T(t0)-Tc)×e-k(t-t0)

(10)

式中：t0為初始迭代次數；T(t0)為物體的初始溫度，℃；T(t)為當前時刻t的物體溫度，℃；Tc為周圍環境溫度，℃；k為衰減系數，是1個常數；t-t0為時間差，可以用迭代次數刻畫，可與公式(9)保持一致。以迭代次數作為橫坐標、物體溫度作為縱坐標，取初始溫度為100 ℃，衰減系數為0.001，繪出溫度隨迭代次數的變化曲線圖，如圖2所示。同時將指數衰減函數畫在同一個坐標系下，以便于對比。

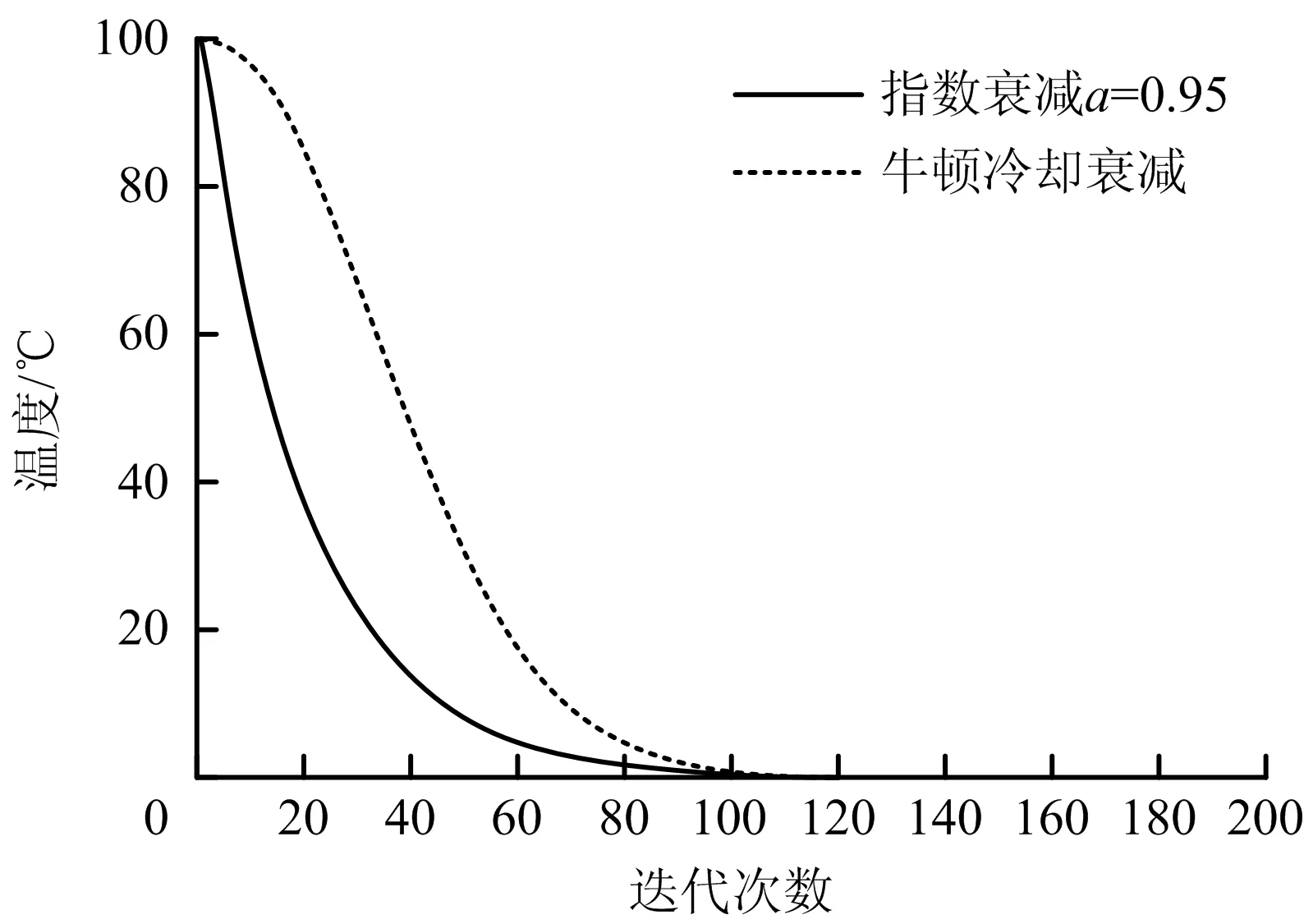
圖2 不同衰減函數的溫度衰減趨勢Fig.2 Temperature attenuation trends of different attenuation functions

由圖2可知，在相同的迭代次數下，牛頓冷卻衰減函數相較于指數衰減函數溫度更高，這可以在算法初期以更高的概率接受較差的解，從而提高搜索全局最優解的概率。

7)派遣方案選擇

在確定社會組織情況和災區情況之后，根據綜合救援效益和時間成本、經濟成本建立派遣模型，并采用改進的模擬退火算法進行求解，得到最優派遣方案。算法求解流程如圖3所示。

3 實例分析

以地質災害事件為例，利用本文所提出的模型進行計算，找出最優派遣方案。假設某地發生地質災害，有3個受災區，受災程度分別為重度受災區、中度受災區和輕度受災區，其中重度受災區的人員傷亡和房屋倒塌情況比較嚴重，所以急需城市搜救能力和醫療救助能力較強的社會組織；輕度受災區的人員傷亡情況較輕，對城市搜救類的組織需求不大，對后勤保障人員的需求較為迫切。針對上述情況，各災區救援技能需求程度等級情況見表1。

現在有8個具備救援資格的社會組織請求參與本次地質災害救援。8個社會組織的救援技能滿足災區需求的6類救援技能，技能等級分布情況見表2。

各社會組織從不同位置出發，到達災區花費的時間見表3。3個災區的最佳救援時間分別為5，6，7 h。并且前往救援所產生的經濟成本可被估算，社會組織通往不同災區的經濟成本見表4。8個組織的救援預算成本分別為14，13，13，11，13，11，13，15萬元。

圖3 基于改進模擬退火算法的模型求解流程Fig.3 Flow chart of model solving based on improved simulated annealing algorithm

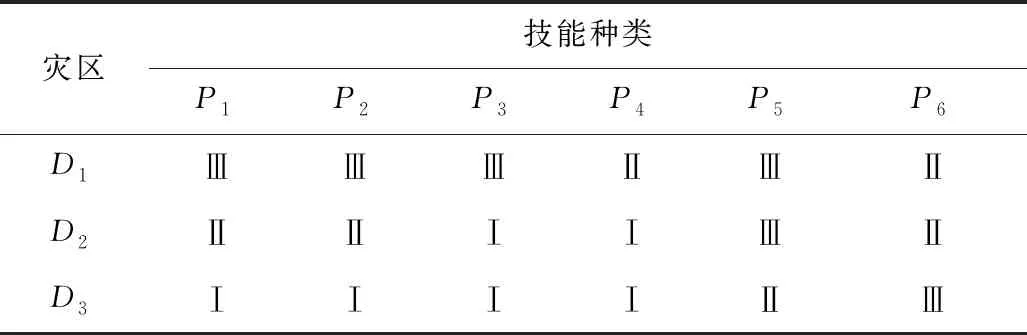
表1 各災區救援技能需求程度的等級情況Table 1 Grades of requirement degree for rescue skills by each disaster area

根據式(1)，計算社會組織對于災區的救援技能匹配度，計算結果見表5。匹配度數值范圍為[0,1]，數值越接近于1，表示救援技能越匹配。

通過改進的模擬退火算法得出最佳派遣方案，根據是否考慮時間約束和經濟約束得出4組派遣方案，見表6～9。其中，方案1考慮時間約束和經濟約束；方案2不考慮時間約束、經濟約束；方案3考慮時間約束、不考慮經濟約束；方案4不考慮時間約束、考慮經濟約束。

表2 社會組織救援技能等級Table 2 Rescue skills grades of social organizations

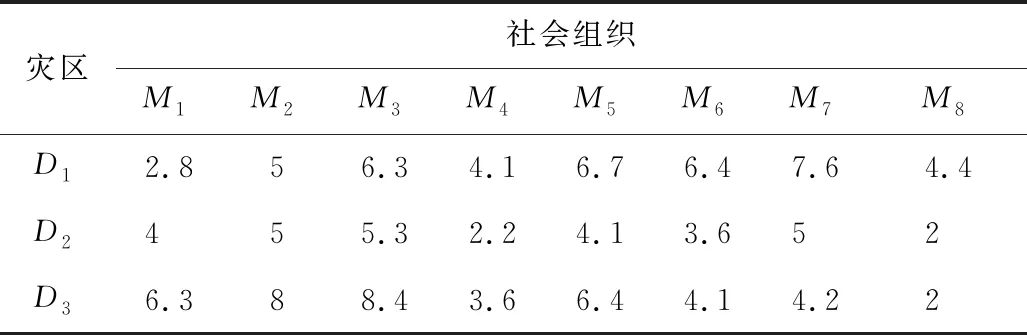
表3 社會組織抵達不同災區花費的時間Table 3 Time for social organizations to arrive at different disaster areas h

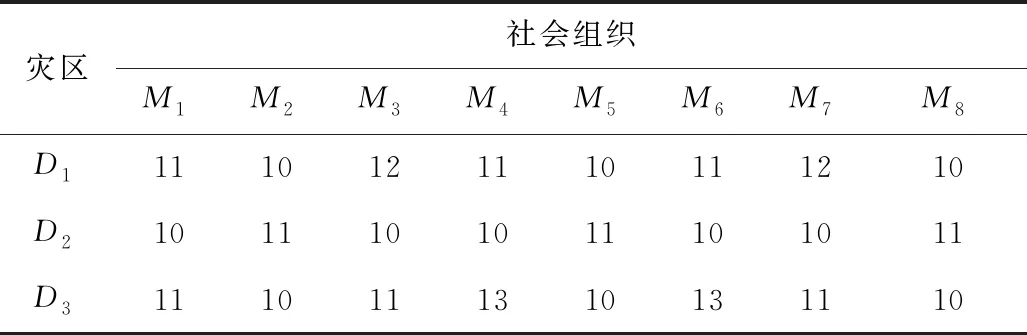
表4 社會組織通往不同災區的經濟成本Table 4 Economic costs of social organizations to different disaster areas 萬元

表5 救援技能匹配度Table 5 Matching degree of rescue skills

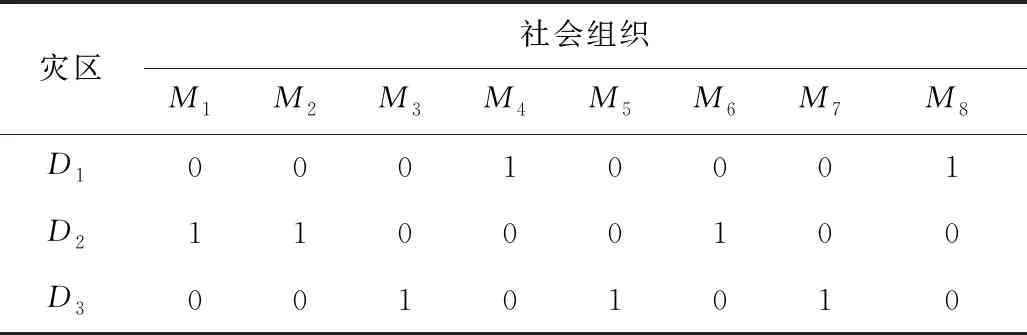
表6 模擬退火算法對模型的求解結果(方案1)Table 6 Solving results of simulated annealing algorithm to model (scheme 1)

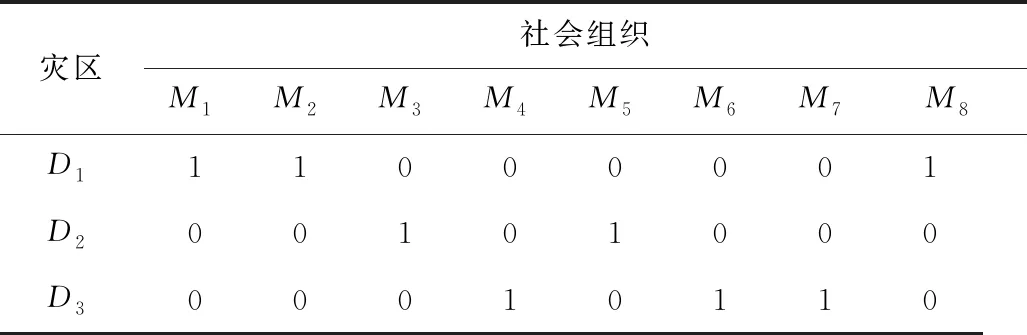
表7 模擬退火算法對模型的求解結果(方案2)Table 7 Solving results of simulated annealing algorithm to model (scheme 2)

表8 模擬退火算法對模型的求解結果(方案3)Table 8 Solving results of simulated annealing algorithm to model (scheme 3)

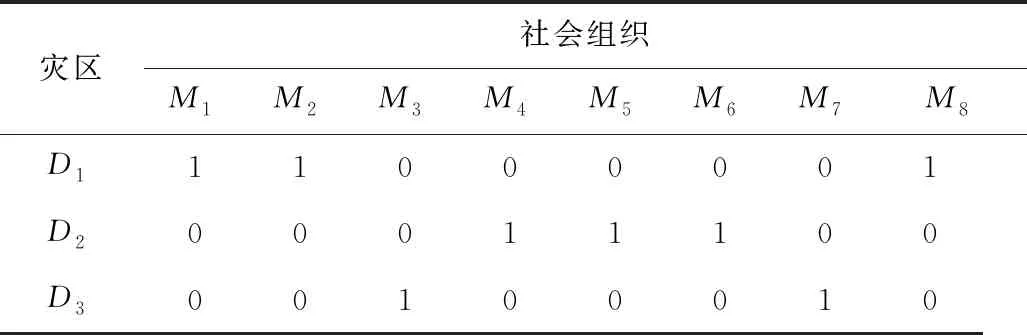
表9 模擬退火算法對模型的求解結果(方案4)Table 9 Solving results of simulated annealing algorithm to model (scheme 4)

通過計算求得4個方案的總救援效益、總花費時間和總經濟成本見表10。

從結果中可以看出，考慮時間約束和不考慮時間約束的派遣結果均滿足災區最大救援需求量此約束條件。從救援效益和時間上來看，方案2的總救援效益高于方案1的總救援效益，且其總花費的時間較低，符合時間約束條件；從經濟成本上看，加入經濟成本約束后的派遣結果其花費更低，如方案4與方案3相比，其經濟成本相差4萬元。因此，不同的約束條件可以得出不同的派遣方案，可根據實際情況對時間約束進行調整，以得到最佳派遣策略。

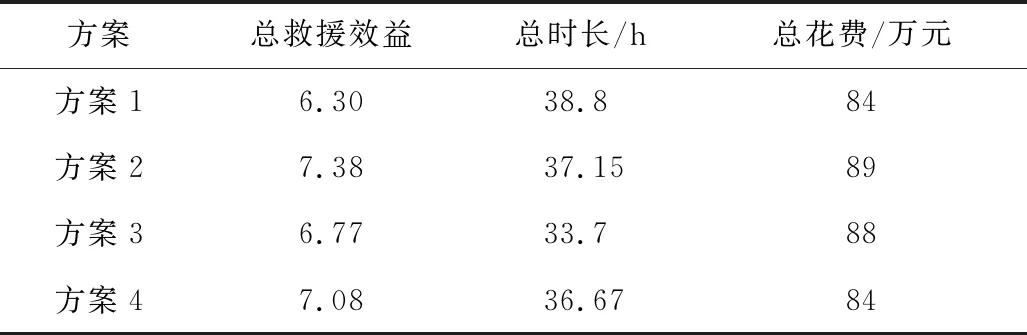
表10 總救援效益、花費時間和經濟成本計算結果Table 10 Calculation results of total rescue benefits,time spent and economic costs

4 結論

1)根據“量力而行、就近就便”等原則，應綜合考慮救援效益、時間成本、經濟成本3個因素建立災后救援派遣模型。

2)采用模擬退火算法對模型進行求解，根據模型改進Metropolis接受準則，并用牛頓冷卻定律作為溫度衰減函數。最后通過算例結果來證實該社會組織救援派遣模型的可行性，為社會組織參與災后救援提供決策支持。

3)根據實際情況調整約束條件，可以得出符合災區救援需求情況的派遣方案。

4)在救援派遣模型建立時，社會組織成員人數未確定，因此模型與實際情況存在一定的誤差，在實際應用時需對個別參數進行修正。