考慮空間變異性的基坑降水支護開挖引起地面沉降的可靠度評估

章潤紅 GOH Anthony 周廷強 仉文崗

摘 要：對于軟黏土或殘積土中的深基坑支護開挖，開挖后的地面沉降與基底隆起和擋墻變形密切相關，且受墻后地下水變化的影響顯著。提出一種基于最新開發的簡化對數回歸模型的可靠性分析方法預測地面最大沉降，采用考慮土體空間變異性的方差縮減技術實現一階可靠性方法（FORM），探討了地面沉降超過既定閾值的概率，驗證了方差縮減技術的高效性。通過分析關于空間平均及關鍵設計參數的影響發現，土體空間變異性會導致較高的破壞概率，擋墻的系統剛度、地面沉降閾值的大小、土體特性的變化系數以及地下水下降深度也對可靠性指標有不同程度的影響，忽略其影響會導致不可靠的設計，較大的特征長度會導致較低的破壞概率和較高的?，同時考慮的空間變異性會比單獨考慮其中一項對影響更大。

關鍵詞：地面沉降;基坑支護開挖;降水;空間變異性;方差縮減

1 Introduction

Rapid urbanization and continuous development of infrastructure construction have led to an increased demand for deep braced excavations in urban built environments. One major concern with the construction of deep excavation support systems is the potential damage to nearby buildings and tunnels caused by excavation-induced ground movement. The ground movement behind the excavation is correlated with the extent of basal heaves and the magnitude of the wall deflections. Ground settlement is an important hydro-geological factor influencing the groundwater drawdown behind the excavation， due to possible leakage through the wall， flow along the wall interface， or poor connections between wall panels as a result of poor quality control. Therefore， assessing the distribution and magnitude of the ground surface settlement adjacent to a braced excavation is the most important consideration in the design phase. Numerical modeling is widely used， but it's time-consuming and requires considerable computational effort， especially three-dimensional computation. The use of empirical/semi-empirical methods to predict excavation-induced ground movement is more convenient [1-10].

Reliability-based analysis via the first-order reliability method （FORM） is increasingly employed in various geotechnical applications [11-13] to calculate the reliability index as well as the probability of failure. This method adopts the mean average and the standard deviation or the equivalent value to present uncertain parameters. The safety factor or safety margin is determined by measuring the shortest distance from the safety average to the directional standard deviation of the most likely failure combination of parameters on the limit state surface. However， natural soil properties vary spatially due to the complicated geological， environmental， and physical-chemical processes to which the soil has been subjected during its formation[14-15]. Several researchers have highlighted the effects of the spatial variation of soil properties on various geotechnical problems[16-21]. Reliability analysis considering spatial variability has been carried out by many researchers. Luo et al.[22] presented a simplified approach for the reliability analysis of basal heave in a braced excavation considering the spatial variability of the soil parameters using the first-order reliability method （FORM）. Wang et al.[23] modeled the inherent spatial variability of the soil properties of drilled shafts by developing a reliability-based design （RBD） approach that integrated a Monte Carlo simulation （MCS）-based RBD with the random field theory. Cheon et al.[24] described the spatial variability of geotechnical properties for foundation design in deep water in the Gulf of Mexico， via a random field model that depicted spatial variations in the design of undrained shear strength. Li et al.[25] investigated the reliability of strip footing in the presence of spatially variable undrained shear strength with a non-stationary random field. Gong et al.[26] proposed a new framework considering the spatial variability of soil properties to analyze the probabilistic ability of a braced excavation in clay， which was modeled with the random field theory. Liu et al.[27] analyzed the reliability of slopes considering the spatial variability of the soil using a simplified framework that applied a strategy of variance reduction to enable more than one shear strength value to be considered in slope reliability problems based on Monte Carlo simulation and the multiple response surface method （MRSM）. However， studies on the probabilistic assessment of ground surface settlement induced by the braced excavation that consider the uncertainties arising from the soil stiffness and strength parameters are limited. In addition， the influence of the spatial variability of soil properties， as well as the influence of groundwater drawdown， are scarcely investigated.

A simple logarithm regression （LR） model based on the numerical results from 746 hypothetical cases[28]， was developed to predict the maximum ground settlement δvm. It is validated by a total of 19 well-documented actual case histories from various sites. The equation for δvm （mm） with the coefficient of determination R2=0.924 5 takes the following form：

The index for the drawdown in the LR analysis was only 0.101 3， which is relatively small compared to the excavation depth， the relative shear strength ratio， and the system stiffness value. Based on Eq. （2）， when other parameters are kept constant， an increase of dw from 0.3 m to 6.0 m will almost double the maximum ground surface settlement， which is consistent with the findings by Wen et al.[35].

3 Reliability analysis considering spatial variability

Since the FE analysis and the proposed LR estimation model are unable to take into account the inherent spatial variability of soil properties， this section introduces a reliability-based method to estimate the braced excavation induced ground surface settlement considering groundwater drawdown by adopting the FORM spreadsheet method and implementing the spatial factors.

3.1 Brief introduction to spatial variability

Spatial variability refers to the nonuniform distribution of basic soil properties such as permeability or the deformation modulus. The change in the spatial average of soil properties in a certain area is smaller than at a certain point， to some extent， and as the size of the area increases， the change in the soil properties decreases. A dimensionless variance reduction function Γ2 calculated by the scale of fluctuation θ and the characteristic length L， as proposed by Vanmarcke[36]， was used to quantify the reduction in the point variance under local averaging. It is subsequently adopted by Vanmarcke to reveal spatial averaging for reliability analysis[37]， by means of which the soil parameter variances can be reduced by multiplying a factor less than the unity， i.e. the variance reduction factor. This variance reduction technique has been successfully applied using different constant， triangular， and exponential models[37-38]， among which the latter is more commonly assumed for geotechnical random field modeling， expressed as：

The reduced variance σ2Γ can be obtained through：

in which σ is the standard deviation of cu/σ′v or E50/cu. In this study， Γ is the standard deviation reduction factor.

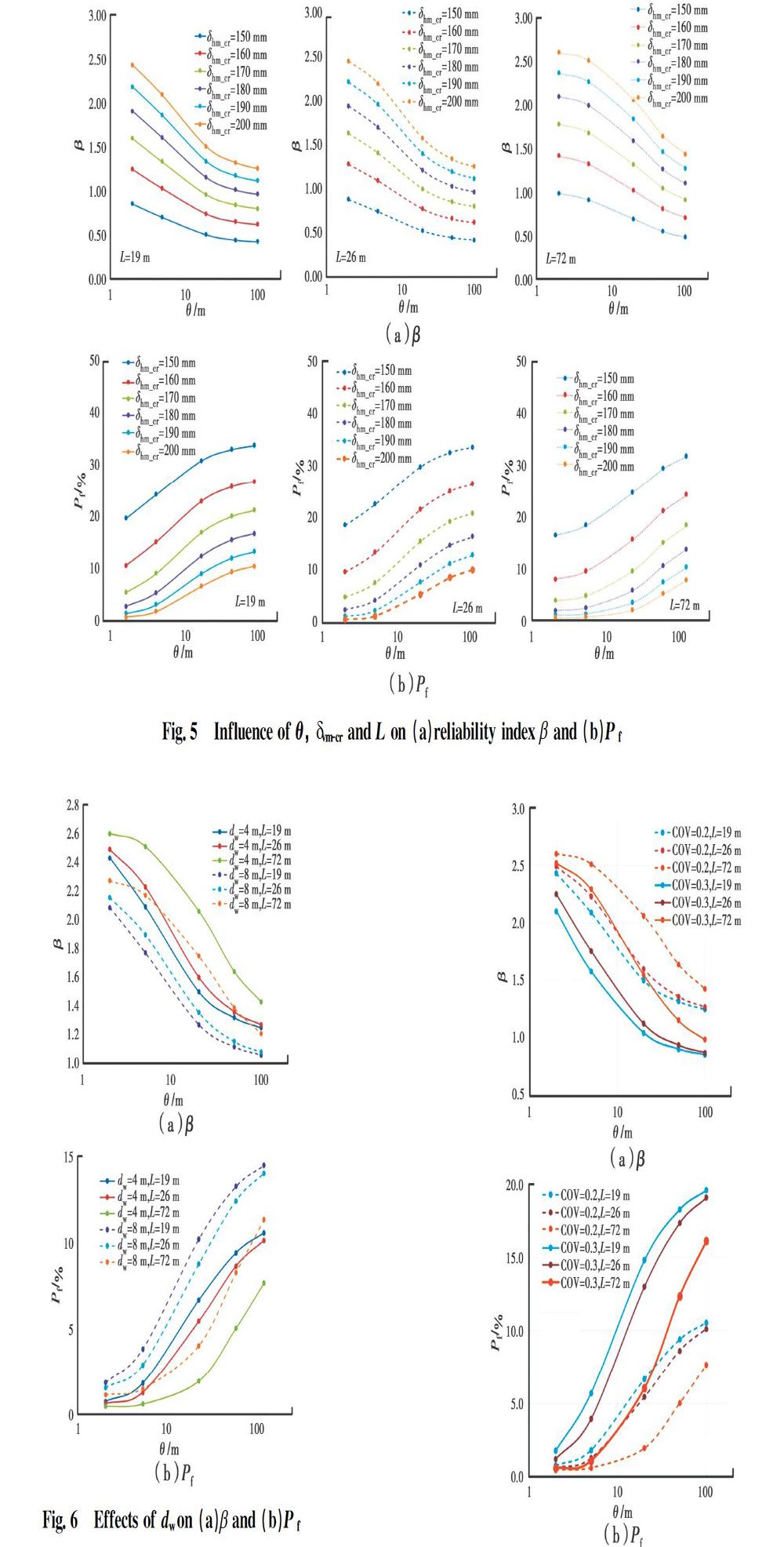
For reliability analysis using the variance reduction technique， the characteristic length is of most importance. Schweiger et al.[39] found that for the analysis of supported excavations， the characteristic length is correlated to the length of the sliding surface. Luo et al.[22] investigated the value of L that should be used and examined the influence of different L on the probability of excavation-induced basal-heave failure. For simplicity， the commonly adopted scale of fluctuation values θ of 2， 5， 20， 50， 100 m[40-41]， and the characteristic lengths L=19， 26， 72 m are considered， which are closely associated with the excavation depth， the diaphragm wall depth， and the final strut depth.

As shown in Fig. 1， the 1st L=19 m is the length of od （the distance of the final strut to the bottom of the diaphragm wall）， the 2nd L=26 m equals the length of the arc cd， and the 3rd L=72 m is the length of the sliding surface （arc abcde）. This method has been similarly adopted by Wu et al.[16]and Luo et al.[22].

3.2 Developed Excel spreadsheet

Fig.2 plots the FORM EXCEL Spreadsheet setup that implements the spatial variability for the calculation of the reliability index??and the probability of failure Pf based on the proposed estimation model of ground surface settlement. The spatial factors are inserted via Cells R3∶S5. The two variables of cuv′ and E50/cu are assumed to be normally distributed. Other parameters including B， T， He， ln S， and dw are assumed to be deterministic. In the example shown in Fig. 2， B=30 m， T=30 m， and He=20 m are adopted in the spatial variability analysis for the detailed use of the developed spreadsheet[13]. The reliability index?is calculated in Cell O4， numerically expressed as Eq. （5）

where x is the vector of random variables; m is the vector of mean values; σ is the vector of standard deviation; R is the correlation matrix; and F is the failure region. Cell g（x） contains the expression of δvm-δvm_cr， which indicates that if the induced maximum ground surface settlement is greater than the threshold value δvm_cr， it would be regarded as a failure or unsatisfactory performance. The column labeled xi contains the design point. For spatial variance， SD=Mean×COV， in which SD is the standard deviation， Mean is the mean value， COV is the coefficient of variation，?is the standard deviation reduction factor. For random variables， the off-diagonal terms are zero. For Gaussian-distributed random variables， a direct relationship exists between??and ?in which Φ is the cumulative normal density function.

5 Summary and conclusions

A reliability-based framework that considers the spatial averaging effect of soil properties is proposed to assess the probability that threshold maximum ground surface settlement is exceeded by combining the FORM spreadsheet and the LR model proposed previously by Zhang et al.[28]. It is concluded that soil spatial variability results in a higher probability of failure （i.e.， a lower reliability index）.

The parametric analysis shows that the spatial variability of soil， the threshold ground settlement， the stiffness of the system， the level of groundwater drawdown， as well as the COV of cu/sv′ and E50/cu have a significant influence on the reliability index. When the spatial variability of both cu/σ′v and E50/cu are considered， the influence on? is more significant. A larger characteristic length results in a lower probability of failure and a higher reliability index. The proposed approach requires much less computational effort in dealing with the spatial variability of soil properties. It is expected that these conclusions will provide useful references and insights for the design of future excavation projects involving spatial variability.

For further study， a detailed characterization of geotechnical model uncertainties， especially from the perspective of the spatial variability of in situ soil properties， is indispensable. The authors are working on this by collecting borehole and bore log information regarding field instrumentation and tests.

Acknowledgements

The authors would like to acknowledge the financial support from National Natural Science Foundation of China （Grant No. 52078086）， Natural Science Foundation of Chongqing （No. cstc2018jcyjAX0632）， Chongqing Engineering Research Center of Disaster Prevention & Control for Banks and Structures in Three Gorges Reservoir Area （No. SXAPGC18YB01）.References：

[1] PECK R B. Deep excavation and tunneling in soft ground [C]//7th International Conference on Soil Mechanics and Foundation Engineering， Sociedad Mexicana deMecanica， Mexico City， 1969： 225-290.

[2] HSIEH P G， OU C Y. Shape of ground surface settlement profiles caused by excavation [J]. Canadian Geotechnical Journal， 1998， 35（6）： 1004-1017.

[3] KUNG G T C， HSIAO E C L， JUANG C H. Evaluation of a simplified small-strain soil model for analysis of excavation-induced movements [J]. Canadian Geotechnical Journal， 2007， 44（6）： 726-736.

[17] FAN H J， LIANG R. Reliability-based design of laterally loaded piles considering soil spatial variability [C]//Geo-Congress 2013. March 3-7， 2013， San Diego， California， USA. Reston， VA， USA： American Society of Civil Engineers， 2013： 475-486.

[18] XIAO T， LI D Q， CAO Z J， et al. CPT-based probabilistic characterization of three-dimensional spatial variability using MLE [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2018， 144（5）： 04018023.

[19] CHING J， HU Y G， PHOON K K. Effective Young's modulus of a spatially variable soil mass under a footing [J]. Structural Safety， 2018， 73： 99-113.

[20] GOH A T C， ZHANG W G， WONG K S. Deterministic and reliability analysis of basal heave stability for excavation in spatial variable soils [J]. Computers and Geotechnics， 2019， 108： 152-160.

[21] CHEN F Y， WANG L， ZHANG W G. Reliability assessment on stability of tunnelling perpendicularly beneath an existing tunnel considering spatial variabilities of rock mass properties [J]. Tunnelling and Underground Space Technology， 2019， 88： 276-289.

[22] LUO Z， ATAMTURKTUR S， CAI Y Q， et al. Simplified approach for reliability-based design against basal-heave failure in braced excavations considering spatial effect [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2012， 138（4）： 441-450.

[23] WANG Y， CAO Z J. Expanded reliability-based design of piles in spatially variable soil using efficient Monte Carlo simulations [J]. Soils and Foundations， 2013， 53（6）： 820-834.

[24] CHEON J Y， GILBERT R B. Modeling spatial variability in offshore geotechnical properties for reliability-based foundation design [J]. Structural Safety， 2014， 49： 18-26.

[25] LI D Q， QI X H， CAO Z J， et al. Reliability analysis of strip footing considering spatially variable undrained shear strength that linearly increases with depth [J]. Soils and Foundations， 2015， 55（4）： 866-880.

[26] GONG W， JUANG C H， MARTIN J R. A new framework for probabilistic analysis of the performance of a supported excavation in clay considering spatial variability [J]. Géotechnique， 2017， 67（6）： 546-552.

[27] LIU L L， DENG Z P， ZHANG S H， et al. Simplified framework for system reliability analysis of slopes in spatially variable soils [J]. Engineering Geology， 2018， 239： 330-343.

[28] ZHANG R H， ZHANG W G， GOH A T C， et al. A simple model for ground surface settlement induced by braced excavation subjected to a significant groundwater drawdown [J]. Geomechanics and Engineering， 2018， 16（6）： 635-642.

[29] BRINKGREVE L B J， KUMARSWAMY S， SWOLFS W M. Plaxis 2D user manual [M]. PLAXIS bv， Netherlands， 2016.

[30] HASHASH Y M A， WHITTLE A J. Ground movement prediction for deep excavations in soft clay [J]. Journal of Geotechnical Engineering， 1996， 122（6）： 474-486.

[31] LAM S Y. Ground movements due to excavation in clay： physical and analytical models [D]. University of Cambridge， UK， 2010.

[32] ZHANG W G， GOH A T C， XUAN F. A simple prediction model for wall deflection caused by braced excavation in clays [J]. Computers and Geotechnics， 2015， 63： 67-72.

[33] WROTH C P， HOULSBY G T. Soil mechanics-property characterization and analysis procedures [C]//Proceedings of the 11th International Conference on Soil Mechanics and Foundations Engineering， San Francisco， California， U.S.A.， 1985.

[34] XUAN F. Behavior of diaphragm walls in clays and reliablity analysis[D]. Nanyang Technological University， 2009.

[35] WEN D Z， LIN K Q. The effect of deep excavation on pore water pressure changes in the Old Alluvium and under-drainage of marine clay in Singapore [M]//Geotechnical Aspects of Underground Construction in Soft Ground. Specifique， Lyon， 2002.

[36] VANMARCKE E H. Probabilistic modeling of soil profiles [J] Journal of the Geotechnical Engineering Division， 1977， 103（11）， 1227-1246.

[37] VANMARCKE E H. Random Fields： Analysis and synthesis [M]. 2nd ed. Hoboken， NJ： John Wiley & Sons， 2010.

[38] RACKWITZ R. Reviewing probabilistic soils modelling [J]. Computers and Geotechnics， 2000， 26（3/4）： 199-223.

[39] SCHWEIGER H F， PESCHL G M. Reliability analysis in geotechnics with the random set finite element method [J]. Computers and Geotechnics， 2005， 32（6）： 422-435.

[40] JIANG S H， LI D Q， CAO Z J， et al. Efficient system reliability analysis of slope stability in spatially variable soils using Monte Carlo simulation [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2015， 141（2）： 04014096.

[41] LI X Y， ZHANG L M， GAO L， et al. Simplified slope reliability analysis considering spatial soil variability [J]. Engineering Geology， 2017， 216： 90-97.

（編輯 胡英奎）