基于改進SCGM(1,1)C模型的海上交通事故量預測

杜柏松， 艾萬政， 胡林燕， 朱鵬飛

(浙江海洋大學 船舶與海運學院， 浙江 舟山 316022)

海上交通事故量預測是海事安全評價和決策的基礎，是海上安全管理部門總體控制水上交通安全的核心內容之一。[1]定量研究海上交通事故的變化趨勢，對保障海上交通運輸安全、提高海上交通安全管理水平具有重要的現實意義。目前，用于預測海上交通事故量的預測方法有支持向量機技術預測、BP(Back Propagation)神經網絡預測和回聲狀態網絡預測等預測方法[2-4],這些方法計算繁瑣且需要大量的歷史數據。由于灰色預測理論主要針對含有不確定因素，且具有一定變化趨勢系統問題的預測；海上交通事故量具有隨機性、不確定性等特點，且隨著海上交通規范化和秩序化的發展，自開始統計以來總體呈現下降的趨勢。因此，許多學者利用灰色理論對海上交通事故量進行預測研究。李云表等[5]利用GM(1,1)預測模型對舟山海域的海上交通事故量做了預測，其結果能反映海上交通事故量的變化趨勢，但預測精度有待進一步提高。隨著研究的深入，在灰色預測基礎上建立許多灰色相關組合模型。虞盈等[6]在灰色預測的基礎上，建立灰色馬爾科夫組合模型，該組合模型能很好地克服數據的波動性；范中洲等[7]建立灰色BP神經網絡組合預測模型，其結果比單一灰色預測和BP神經網絡預測在預測精度和穩定方面更佳；徐東星等[8]等提出一種優化背景值和預測值殘差的改進三參數灰色預測模型，取得良好的預測效果；陳昌源等[9]通過引入弱化算子序列對灰色預測的背景值進行優化，預測結果良好。以上灰色預測相關組合模型，在預測計算過程中依然存在預測過程不甚科學、計算過程復雜等特點，預測精度有待進一步提高；GM(1,1)模型是有偏差的預測模型，不能充分利用灰色系統的信息。[10]單因數系統云灰色預測模型(System Cloud erey Model, SCGM(1,1)C)是在GM(1,1)預測的基礎上發展而來的，具有建模過程更加嚴謹，計算過程更簡單、精度更高等特點[11]，該模型被廣泛運用于航空、道路等交通領域[12-13]以及煤礦相關領域[14]的事故量預測研究中，取得良好的預測效果。

為更準確地完成預測研究，本文采用在交通領域事故量預測中運用比較廣泛的SCGM(1,1)C預測模型，并通過相關算法對其進行多角度優化，構建改進的SCGM(1,1)C預測模型，以實現對海上交通事故量的高精度預測。

1 SCGM (1,1)c預測模型的建立

SCGM (1,1)C預測模型是灰色GM(1,1)預測模型的發展，其對原始數列的處理采用積分計算而非GM(1,1)預測模型的累加計算方式，即計算原理由梯形面積替代矩形面積，提高了預測精度。同時，相對于GM(1,1)預測模型，在確定模型參數時SCGM (1,1)C預測模型不需要大量的矩陣運算，且利用預測模型求取預測值時不需累減計算，預測計算過程得到簡化。

SCGM (1,1)C預測模型建模過程如下：

設海上交通事故量樣本數據序列為X(0)，有

X(0)={X(0)(1),X(0)(2)，…，X(0)(n)}

(1)

對樣本序列X(0)進行積分生成變換，得X(0)={X(0)(1),X(0)(2)，…，X(0)(n)},有

(2)

而

X(1)(m)=0.5×[X(0)(m)+X(0)(m+1)]

(3)

設海上交通事故量積分樣本序列X(0)與函數fr(k)=bea(k-1)-c滿意趨勢關聯，用X(0)′的數據貼切擬合于fr(k)，計算可得到云灰色系數為

(4)

(5)

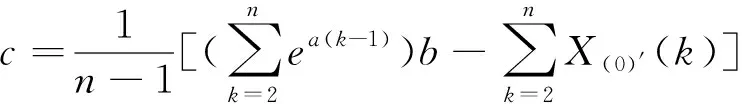
(6)

設X(0)(k)=b-c,U=ac，則有微分方程為

(7)

解該方程得

(8)

對X(0)′(k)進行還原處理，即可得到海上交通事故量的SCGM (1,1)C預測模型為

(9)

2 改進SCGM (1,1)C預測模型

系統SCGM (1,1)C雖然較灰色GM(1,1)預測模型在預測精度和運算過程上有一定提高，但該模型的基本原理是灰色預測，對于因不確定性因素造成的海上交通事故量的波動，該模型依然不能達到理想的預測精度。為提高模型的預測精度，對SCGM (1,1)C模型預測值提出修正。

2.1 馬爾科夫理論修正預測值

樣本值與SCGM (1,1)C模型預測值之差，稱為預測殘差，殘差的分布情況可視為馬爾科夫狀態。[15]馬爾科夫預測是通過計算各狀態的轉移概率來實現的，轉移概率反映各狀態的內在規律，其最顯著的特點是無后效性，尤其適用具有較強波動性樣本數據的預測。因此，將馬爾科夫預測理論與SCGM (1,1)C模型結合起來，利用馬爾科夫理論修正海上交通事故量預測值。

1) 計算海上交通事故量SCGM (1,1)C模型預測值的殘差和相對誤差分別為

(10)

(11)

2) 根據相對誤差Q的分布情況，把其均分為i個數值區間，每個區間為一個預測狀態，有

Ei=[Li,Ui],i=1,2,…,n

(12)

3) 構造轉移概率矩陣，記由狀態Ei轉移到狀態Ej發生nij次，而狀態Ei在相對誤差系列中出現ni次，則由Ei轉移到狀態Ej的狀態轉移概率為pij=nij/ni，可得1步狀態轉移概率矩陣為

(13)

P(n)=(P(1))n

(14)

式(14)為n步狀態轉移概率矩陣。

4) 通過計算狀態轉移概率并比較各個狀態概率的大小，概率最大者為預測年份的狀態。設預測年份狀態為Ei=[Li,Ui]，取狀態Ei的中間值Ii(白化系數λi=0.5)為修正參數，即

Ii=|0.5×(Li+Hi)|

(15)

則可得經過馬爾科夫理論修正的馬爾科夫SCGM (1,1)C預測模型為

(16)

當預測值大于樣本值時，取“+”；當預測值小于樣本值時，取“-”。

2.2 PSO二次修正預測值

由第2.1節馬爾科夫理論修正SCGM (1,1)C預測值的式(15)可知：關于修正參數Ii的取值，人為選取了狀態Ei的中間值，即λi=0.5，但在實際應用中，中間值并非一定是最優值，這樣取值不科學且存在較大誤差。[15]為合理的求解最優修正參數Ii，采用粒子群優化(Particle Swarm Optimization，PSO)算法對λ進行優化。 PSO算法是由Kennedy等提出的基于種群的優化算法，具有全局搜索能力強、參數少，計算過程便于MATLAP實現等優點，其基本算法為

vi(t+1)=wvi(t)+c1rand1(xpbesti-xi(t))+

c2rand2(xgbesti-xi(t))

(17)

xi(t+1)=xi(t)+vi(t+1)

(18)

式(17)和(18)中：xi為時刻t粒子的位置；vi為時刻t粒子的速度；xpbesti為粒子局部最優位置；xgbesti為粒子的全局最優位置；rand1、rand2為取值在(0,1)之間的隨機數；ω為慣性系數；c1和c2為學習因數。

本研究設最優λ為粒子的最優位置x，以均方誤差(Mean Square Error, MSE)表示為

(19)

MSE為適應度函數，通過MATLAP編程運算求解粒子的最優位置x值，即為最佳的λ。從而可得經過優化的修正參數為

(20)

將優化后的修正參數Ii代入式(15)即可得海上交通事故量的改進SCGM (1,1)C預測模型。

2.3 改進SCGM (1,1)C預測模型建模過程

梳理以上SCGM (1,1)C模型建模過程及對其進行的2次優化，可總結改進SCGM (1,1)C預測模型的建模流程，見圖1。

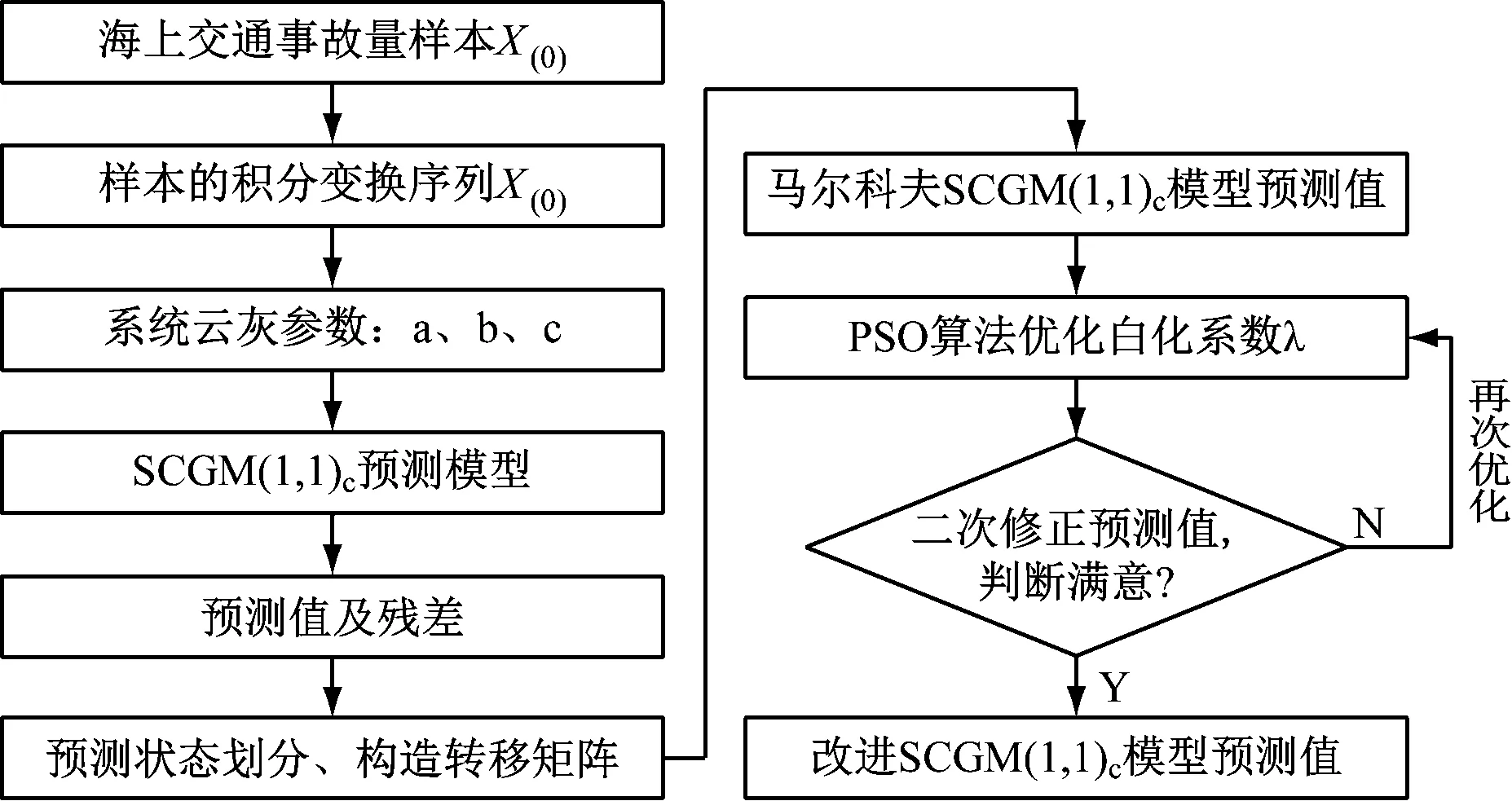
圖1 改進SCGM(1,1)C預測模型的建模流程

2.4 模型檢驗

為驗證改進SCGM(1,1)C模型的預測精度，應采取一定的檢驗方法對其進行檢驗。SCGM(1,1)C預測的原理為灰色預測，灰色預測常用的檢驗方法為殘差校驗和后驗差校驗[11]，因此，本文也選用這2種方法檢驗改進的預測模型。

2.4.1殘差檢驗及指標

1) 最大絕對百分比誤差(Absolute Percentage Error, APE)，體現模型預測值與樣本數據的最大偏差，有

(21)

2) 平均相對誤差(Mean Absolwte Percentage Error, MAPE)，體現不同模型對相同樣本數據擬合程度的好壞，有

(22)

2.4.2后驗差檢驗及指標

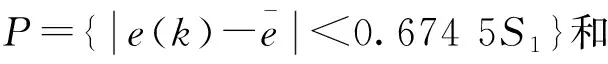
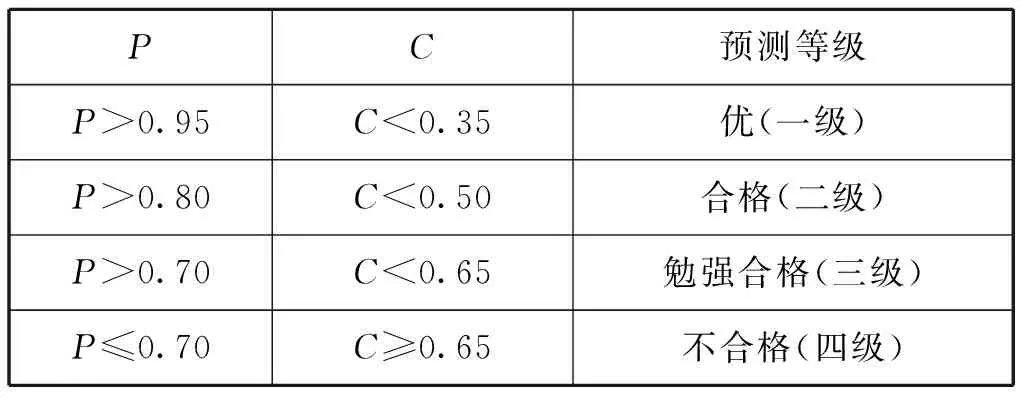
表1 預測模型等級劃分表

3 實例分析

選取2004—2019年的海上交通事故量數據為試驗對象(見表2)，對建立的模型進行實例驗證和分析。根據改進SCGM(1,1)C預測模型的建模過程，以2004—2015數據為樣本數據，通過建立SCGM(1,1)C預測模型及對其進行2次優化模型，分別計算相應的預測值并作擬合曲線，分析并判斷改進模型的精度情況；同時，以文獻[8]所建模型為比較對象，判斷所建模型的準確性，并用所建改進模型對2016—2019年的數據進行實際預測，判斷模型的可行性。

3.1 海上交通事故量的SCGM(1,1)C模型

取2004—2015年的海上交通事故量數據為樣本數據X(0)，有

X(0)={562,532,440,420,342,358,331,298,270,262,260,212}

(23)

表2 2004—2019年海上交通事故量 起

由式(2)～式(6)得SCGM(1,1)C模型灰參數：a=-0.094 3,b=-5 990.68,c=-5 970.92；代入式(8)得預測模型為

(24)

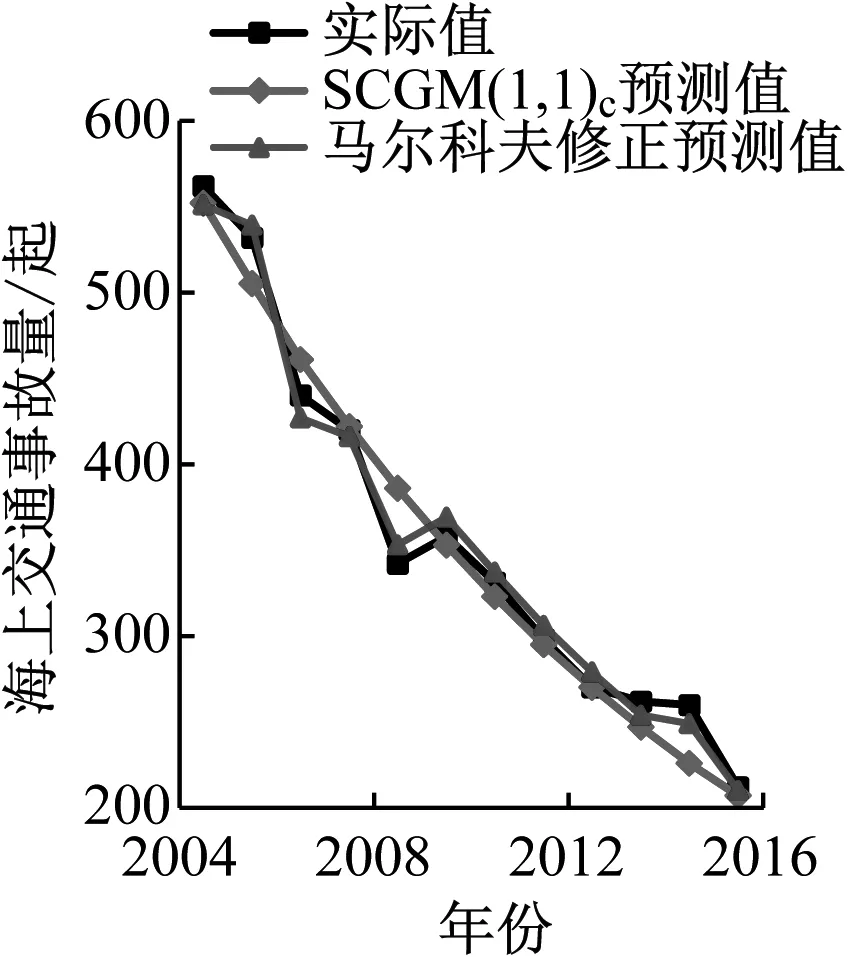
根據模型計算求解預測值，并計算e(k)和Q，見表3。3種預測模型擬合曲線圖見圖2。

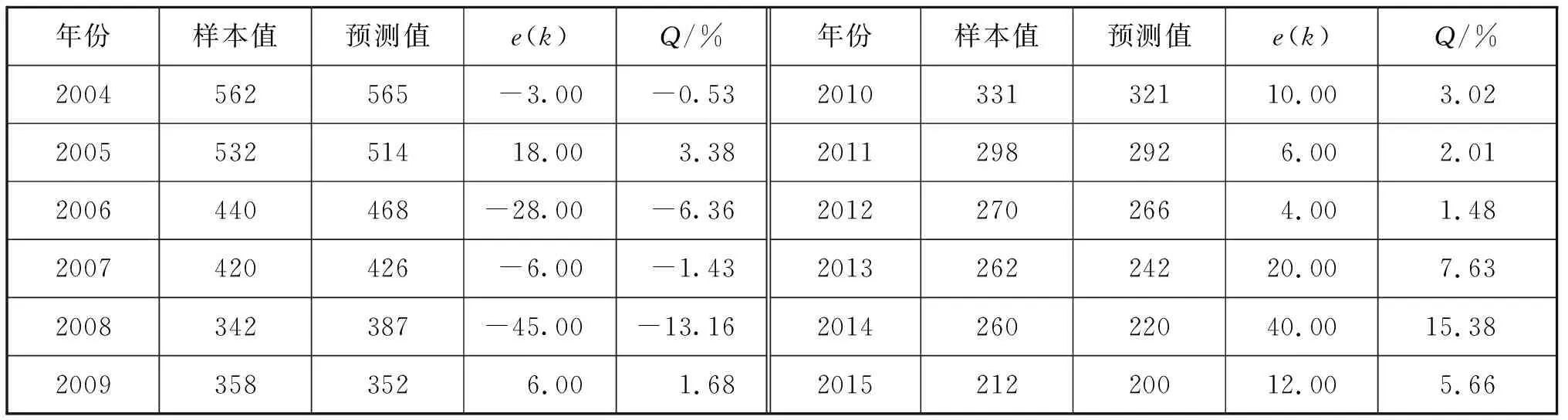
表3 SCGM(1,1)C模型預測結果 起

由表3可知：2008年和2014年、2015年因樣本值數據波動較大，預測產生較大的預測誤差。由圖2可知：預測值擬合曲線在2005—2009年和2013—2015年2個時間段背離明顯。因此，SCGM(1,1)C模型有待改進。

3.2 馬爾科夫理論修正預測值

為提高SCGM(1,1)C模型的預測精度，對該預測模型進行馬爾科夫理論修正。由上文馬爾科夫修正模型的建模過程，根據表3所列SCGM(1,1)C模型預測值相對誤差的大小分布，把該模型預測值的情況劃分為4個狀態，見表4。

表4 SCGM(1,1)C模型預測值狀態劃分

由表4狀態劃分可得1步狀態轉移概率矩陣為

(25)

在確定各樣本數據年份的預測狀態和轉移概率矩陣以后，即可利用馬爾科夫理論對SCGM(1,1)C預測值進行修正：2004—2015年的預測值狀態已知，因此，可直接通過式(15)和式(16)計算，修正的預測值見表5。對于2015及以后的預測值，首先利用SCGM(1,1)C模型求出預測值，然后以2011年、2012年、2013年和2014年作為馬爾科夫預測狀態的基礎，由基礎年份狀態和多步轉移概率矩陣得到累積概率并判斷預測年份的狀態，最后利用式(15)和式(16)計算。[16]

表5 不同慣性系數ω下改進SCGM(1,1)C預測值的MAEP

3.3 PSO算法二次修正預測值

為進一步提高SCGM(1,1)C預測值的精度，在馬爾科夫理論修正預測值的基礎上，使用PSO算法對其進行二次修正。根據建模過程及式(17)和式(18)，求解最優λ值。

本研究發現，黃油的固體脂肪含量比豬油高，有更好可塑性，同時與豬油相比，烘焙溫度和循環加熱次數的增加對黃油的酸價、過氧化值及多不飽和脂肪酸含量影響不顯著（P＞0.05），這說明黃油在不同烘焙條件下具有良好的穩定性，但高溫處理及多次加熱會使黃油的單不飽和脂肪酸和飽和脂肪酸含量增多，因此，也應盡量避免黃油的重復利用并適當減少烘焙溫度。

1) 首先設置PSO算法各參數，由表4可知：對 SCGM(1,1)C模型預測值的殘差劃分了4個狀態，因此，取搜索維度D=4；由第2.2節所述，設最優λ(0≤λ≤1)為粒子更新位置x，所以取粒子更新位置xmax=1，xmin=0；PSO中種群粒子數和迭代次數越高，其優化效果就越好，但過高的粒子數和迭代次數會延長運算時間，因此，在保證精度效果和運算速度的情況下，取粒子數N=1 000,迭代次數k=1 000。[17]學習因數通常取c1=2、c2=2，且慣性系數0.6≤ω≤1.2時，PSO算法的搜索效率和搜索精度較高，且算法的收斂速度較快。[18]

2) 為取得最佳ω值，在以上各參數確定的情況下，分別取ω=0.6，0.7，…，1.2，編輯海上交通事故量粒子群優化MATLAP程序語言，并多次運行該程序，得到不同的λi，計算各ω值下的改進SCGM(1,1)C模型預測值的MAEP如表5所示。由表5可知：慣性系數為0.8時，改進模型預測值的平均誤差最小，因此，取參數ω=0.8。

由上述參數運用MATLAP編程計算得：λ1=0.506 4；λ2=0.262 1；λ3=0.459 6；λ4=0.000 2，代入式(20)，再根據式(16)，可得經過PSO算法二次修正的預測值，即改進SCGM(1,1)C模型預測值，見表6。

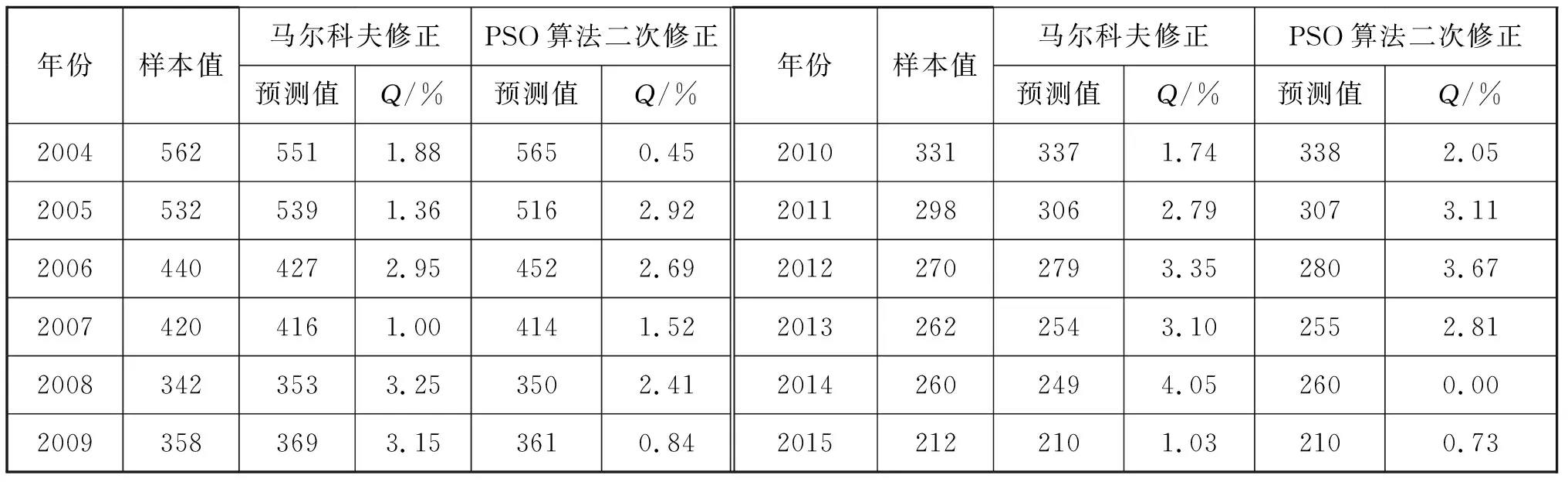
表6 改進SCGM(1,1)C模型預測值 起

3.4 預測模型的精度分析

為驗證SCGM(1,1)C預測模型及其改進模型的精度情況，計算各模型殘差檢驗和后驗差指標，見表7。

由表7和表1可知：新建的海上交通事故量SCGM(1,1)C預測模型達到“優”的一級標準，說明SCGM(1,1)C預測模型是適合與海上交通事故量的預測的；但該模型的殘差指標MAEP=5.14%和APEmax=15.38%均較大，說明模型的精度有待提高。對模型進行馬爾可夫理論修正后，修正模型的后驗差指標C=0.09較單一模型的C=0.24有大幅度降低；同時，MAEP和APEmax兩項指標值也大幅下降，說明經過一次修正后的模型預測精度有很大提高。分析經PSO算法優化二次修正的改進SCGM(1,1)C模型的精度情況，由表7可知：該模型相對于經馬爾可夫修正模型的精度又有了進一步提高。

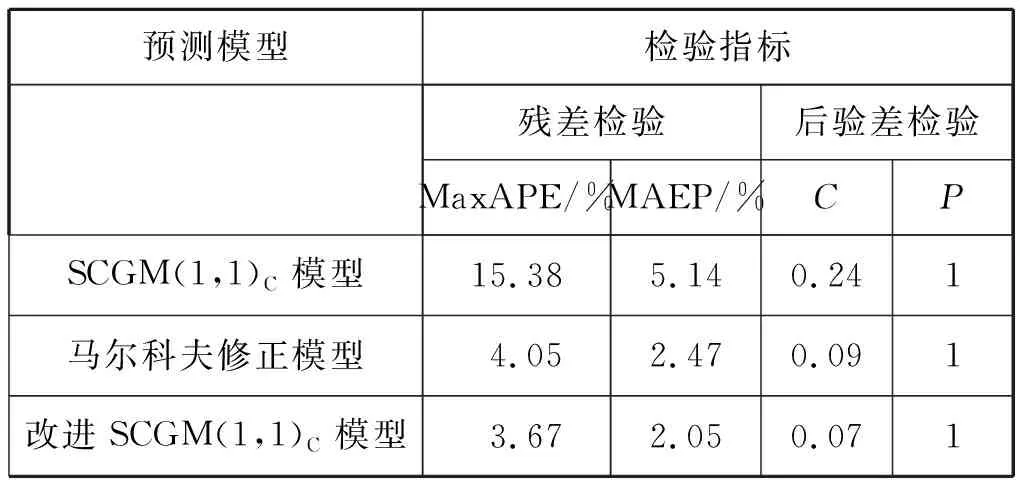
表7 SCGM(1,1)C模型和2個修正模型的預測精度比較

通過比對反映預測模型預測精度綜合情況的MAEP指標：改進SCGM(1,1)C預測模型較馬爾科夫修正模型的精度提高17.00%，較單一SCGM(1,1)C預測模型的精度提高60.12%；由圖2可知：改進模型的擬合曲線與樣本值曲線擬合度更高。綜上所述，新建的改進SCGM(1,1)C模型是合理的。

為驗證驗證改進SCGM(1,1)C預測模型的實用性，用建立的模型對2016—2019海上交通事故量進行預測，結果見表8。由表8可知：2016年預測值精度滿意，2017—2019年預測精度約維持在9%，精度一般，說明SCGM(1,1)C預測模型對短期預測有良好的預測效果，中長期預測精度有待提高。SCGM(1,1)C預測模型的理論基礎是灰色預測，而短期預測精度較高，中長期預測精度一般也正是灰色預測的不足之處。[9]

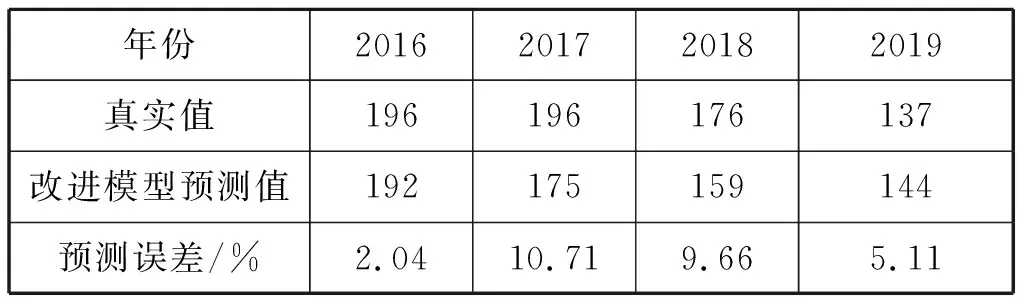
表8 改進SCGM(1,1)C模型的實用性驗證

4 結束語

1) 系統云灰色SCGM(1,1)C預測模型能反映海上交通事故量的總體變化趨勢，可用于海上交通事故量的預測，但通過建模和實例預測分析發現，該模型對具有波動性較大統計量的灰色系統問題，預測精度較低。

2) 馬爾科夫預測理論可有效地克服SCGM(1,1)C預測模型對于灰色系統波動性問題預測的不足；PSO算法對白化系數取值的優化，使馬爾科夫預測理論修正變得更加科學和合理，3者結合構建的組合模型的預測精度得到大幅度提高。

3) 對于改進SCGM(1,1)C預測模型中長期預測精度不高的問題，計劃用近期預測值再訓練，預測下一個預測值以提高精度(即卡爾曼濾波的原理算法)，以及在預測過程中不斷更新樣本數據，利用相關算法對改進的預測模型進行再優化，這是今后研究和學習的方向。