改進的單形進化算法及在神經網絡上的應用研究

全海燕，易 昭，鄭蒙福

(昆明理工大學 信息工程與自動化學院，昆明 650504)

1 引 言

神經網絡是一種模擬人類思維的智能算法模型，可以從輸入數據、信號中學習其中的規律，但自身存在學習能力不足等缺點.

針對神經網絡的不足，許多智能優化算法被應用于神經網絡優化中，如煙火算法(Fireworks Algorithm，FWA)[1,2]、差分進化算法(Differential Evolution Algorithm，DE)[3,4]、蟻群算法(Ant Colony Optimization，ACO)[5,6]、遺傳算法(Genetic Algorithm，GA)[7,8]、粒子群算法(Particle Swarm Optimization，PSO)[9,10]，這些算法由于本身也存在一些缺點，因此許多學者對這些算法進行了改進.鄭夏等人[11]為了提高差分進化算法的性能，引入生物地理學優化算法；劉鑫等人[12]為了改善人工蜂群算法存在的不足，引入粒子群算法；賈云璐等人[13]為了提高優化算法的適應性，提出一種改進的布谷鳥算法.

大多數算法通過引入控制參數實現算法的性能，因此增加算法復雜度.Quan等[14]提出了一種新型的智能優化算法--單形進化算法(SSSE)，SSSE算法通過建立多角色態搜索策略與單形鄰域搜索機制，融合群體協作搜索與競爭選擇進化策略，有效地求解最優化問題，SSSE算法具有結構簡單，控制參數較少，僅有群體數量一個控制參數，并能靈活地跳出局部極值，且有較好的全局搜索的特性.

為了進一步較好地平衡SSSE算法的開采能力和勘探能力，本文提出了一種改進的單形進化算法(Improved Surface-Simplex Swarm Evolution Algorithm，簡稱ISSSE)，ISSSE算法對SSSE算法的多態平衡搜索的方法作了如下改進：一是將粒子的開采態和中心態以均勻分布的方式選取以提高算法的收斂速度和對解的開發能力；二是將粒子的勘探角色態以均勻分布的方式選取以增強當前種群鄰域的勘探和跳出局部最優解的能力.與其他智能優化算法相比較，ISSSE有較高的全局搜索能力，并且改進的算法保持原有僅有一個控制參數的優點.

為提高神經網絡的分類性能，將ISSSE算法引入到RBF神經網絡中，提出基于改進單形進化算法的RBF神經網絡(ISSSE-RBF)，然后用UCI標準數據集對優化后的RBF神經網絡進行學習，得到RBF的最優權值、偏置和徑向基中心.

2 單形進化算法

SSSE算法的實現原理是：基于隨機選取的二維子空間，利用定義的粒子單形鄰域，實現凸集逼近搜索，提高粒子勘探局部區域與算法收斂性的性能，同時在搜索策略中引入粒子多角色態，實現粒子多樣化，提高搜索的全局性[15].

2.1 粒子的二維單形鄰域

粒子的二維單形鄰域是以均勻分布方式隨機選取兩個維度(此處兩個維度用p、q表示)構建而成，在p、q空間內，搜索算子定義方式如式(1)-式(4)所示:

(1)

(2)

(3)

(4)

2.2 粒子的多角色態

每個粒子可以適度地向3個方向演化：自身鄰域、其他粒子位置、最佳粒子位置.如果粒子同時具有3個位置狀態：它自己的最佳位置，新找到的位置和隨機找到的位置，并選擇不同的狀態來建立粒子的單形鄰域，那么粒子不僅可以將每個粒子的局部區域開發到更準確的優化位置，同時也勘探整個目標空間來尋找全局優化的位置.

基于上述思想，通過目標函數的值分別評估四個新找到的位置，同時，粒子i選擇3個位置狀態來描述自己的位置，每個位置狀態的定義如下：

1)中心角色態：定義為搜索到的最優位置.

2)開采角色態：定義為搜索到的最新位置.

3)勘探角色態：定義為在搜索空間隨機定位的位置.

3 改進的單形進化算法

3.1 改進單形進化的原理

整個ISSSE算法的具體步驟如下：

步驟 1.對m個粒子進行隨機初始化，方式為：

步驟 2.對于群體中的每個粒子i，以均勻分布方式隨機選取兩個維度p、q構建搜索子空間R2，按照式(5)-式(8)所示更新粒子位置：

(5)

(6)

(7)

(8)

步驟 3.更新每個粒子在Rn上的4個新中心角色位置，如式(9)-式(12)所示：

(9)

(10)

(11)

(12)

步驟 4.由測試函數f(x)判斷群體搜到粒子的優劣，以此確定粒子的3個角色態：

1)中心角色態：xic(t+1)；

2)開采角色態：xil(t+1)={xic1(t+1),xic2(t+1),xic3(t+1),xic4(t+1)}；

3)勘探角色態：xig(t+1).

步驟 5.記錄群體中最優粒子xoc(t+1)的位置，返回步驟2，直到最優位置收斂到穩定不變的給定精度.

3.2 測試函數

為驗證改進算法的性能，使用如表1所示的測試函數進行測試.

表1中的f1和f2是單峰函數，可測試算法的收斂精度；f3因極值點在陡峭的峽谷很難獲取正確的搜索方向；f4～f7具有多個局部極值，可測試算法的全局搜索能力；f8因震蕩劇烈難以找到全局最優值.

表1 測試函數Table 1 Test functions

3.3 性能測試與研究

本節中，測試參數m對ISSSE性能的影響，并用表1的標準測試函數證明ISSSE的可靠性.粒子數過多時會限制算法的收斂速度，降低算法的效率，在實驗中不考慮m=50的情況.取m=10，20，30，40，并獨立運行50次得到的收斂曲線如圖1(a)-圖1(h)所示.

由圖1(a)-圖1(h)可知，隨著ISSSE算法的唯一參數--群體粒子數量m的增加，ISSSE算法可以在較少迭代次數的情況下，得到更高精度的解，且在取m=40時解的精度最高，取m=10時解的收斂精度和收斂速度最差.

圖1 ISSSE求解f1-f8函數的收斂曲線Fig.1 Convergence curves of the ISSSE function f1-f8

此外，為了更好地顯示ISSSE算法的性能，將它與SSSE和一些新的算法[14,16，17]進行求解精度的對比，為了公平起見，使用文獻[14]中的參數：m=30，對f1～f8進行50次獨立運行，實驗結果如表2所示.

由表2知，對大部分函數ISSSE算法在均值上比其他算法小，有較好的求解精度；ISSSE算法在標準差上比其他算法小，有較好的可靠性.

表2 獨立運行50次的求解精度Table 2 Solution accuracy of 50 independent runs

3.4 解的精度分析

將ISSSE算法與SFFCS[13]算法作性能比較，實驗結果如表3所示.

實驗條件設置一致：適應度計算次數FCmax=3×105，f1～f8分別獨立運行100次，迭代次數為75000，ISSSE的參數設置為：40.

從表3可看出，對單峰函數f1和f2來說，ISSSE算法提高了解的精度，并顯示出較高的穩定性，其中，在f1上，ISSSE取得了全局最優解，在f2上，ISSSE算法取得解的均值和方差比SFFCS算法高出7個數量級，顯示出較高精度和穩定性.在f3上，ISSSE算法的精度和穩定性略差于SFFCS算法.在有眾多局部極值點的多峰函數f4～f8中，ISSSE均表現出較高的精度和較高的穩定性，其中，在f4上，ISSSE算法取得解的精度比SFFCS算法高出1個數量級，在f5～f8上，ISSSE取得全局最優解.

表3 FC相同時最優解的統計值Table 3 Statistics of the optimal solution when FC is the same

3.5 收斂速度分析

收斂誤差ε均設置為10-5時，兩種算法的適應度計算次數的統計值如表4所示，為了公平起見，對f1～f8獨立運行100次.

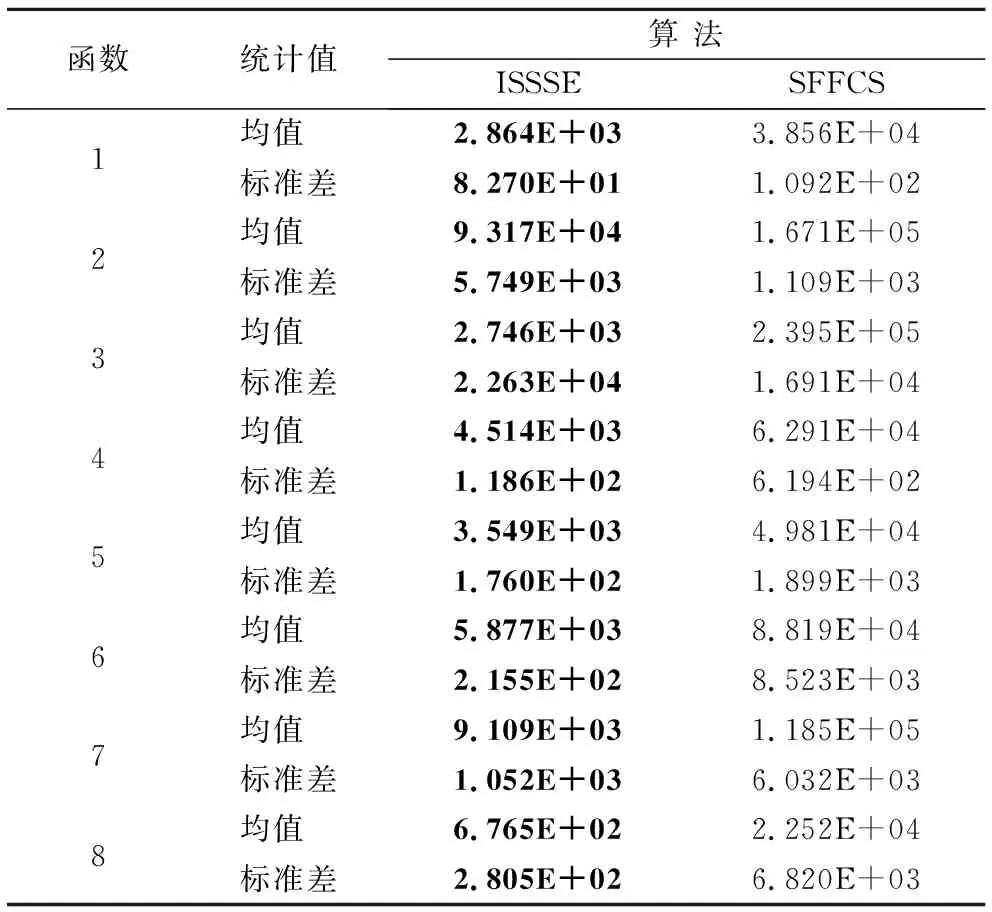
表4 收斂誤差相同時FC的統計值Table 4 Statistics of FC when convergence error is the same

從表4可看出，在單峰函數和復雜的多峰函數中，ISSSE算法和SFFCS算法都能收斂到指定的誤差范圍內，但是ISSSE算法的標準差比SFFCS算法小，說明ISSSE算法比SFFCS算法更穩定，收斂速度更快.

為直觀的顯示原算法和改進算法的收斂速度及勘探能力，將兩種算法指定相同的收斂誤差，得出部分函數(f6～f8)的收斂過程如圖2(a)-圖2(c)所示.從圖2(a)-圖2(c)可以看出：該算法表現出較高的求解能力和較快的收斂速度，前期的曲線趨于平穩，有陷入局部最優解的可能性，隨著迭代次數的增加，粒子靈活地跳出了局部區域，表現出了較好的勘探能力.

圖2 ISSSE和SSSE求解f6-f8函數的收斂曲線Fig.2 Convergence curve of ISSSE and SSSE for f6- f8 function

總體而言，對多數函數而言，ISSSE算法優于其他算法，表現出較好的收斂速度和求精能力.

4 基于改進單形進化的RBF神經網絡算法

智能算法優化RBF的原理是：在搜索空間不斷搜索并調整RBF結構參數使網絡輸出達到期望值，其中結構參數包括兩部分：一是隱含層每一個RBF函數的中心C，二是權值W和偏置B.

基于ISSSE算法的RBF神經網絡訓練算法的步驟如下：

2)對數據進行預處理.訓練集樣本的輸入矩陣A、輸出矩陣Y，定義如下：

其中，M為樣本數，Q為特征數，N為輸出神經元數.

3)定義本文中RBF神經網絡誤差函數為：

4)輸入樣本訓練神經網絡，利用本文提出的ISSSE算法搜索并記錄群體中當前最優粒子的位置:Wo,c(n+1)、Bo,c(n+1)、Co,c(n+1).

5)判斷網絡誤差函數收斂到指定精度或迭代次數到最大次數，則停止搜索，反之，返回第4)步.

6)在指定精度或最大迭代次數搜到的最優粒子位置作為C、W、B的訓練結果.

7)輸入測試樣本，得到測試分類結果.

5 基于優化RBF神經網絡的仿真結果

采用UCI機器學習數據集里的3組數據對本文所提算法進行驗證，分別是Iris、Seed、Wine，將這3個數據集分別用ISSSE-RBF和SSSE-RBF神經網絡進行10次獨立測試.算法的參數設置為：群體數量統一設置為20，最大迭代次數為1000，權值、偏置和中心的搜索空間為[-1,1].統計10次測試樣本分類準確率的最好值(Best)、最差值(Worst)和平均值(Mean)，如表5所示.兩種方法的訓練3個樣本的誤差迭代圖，如圖3(a)-圖3(c)所示.

表5 3種數據集的分類結果Table 5 Classification results of three data sets

圖3 3種數據集的誤差迭代圖Fig.3 Error iteration graphs of three data sets

從圖3(a)-圖3(c)可知，ISSSE-RBF比SSSE-RBF跳出局部最優值的能力較強，說明改進的單形進化算法具有更好的勘探和開采能力，在RBF神經網絡參數尋優上更有優勢.從表5可知，在三個數據集上，基于改進的單形進化算法的RBF神經網絡的平均識別率、最好識別率和最差識別率上，均優于基于單形進化算法的RBF神經網絡，表明ISSSE-RBF在尋優能力上更加穩定，尋優的精度更高.

6 結論與展望

改進的單形進化算法在保留了SSSE算法結構簡單、控制參數唯一、全隨機性、全覆蓋性等優點的基礎上，對算法的單形鄰域搜索算子上做了改進，提高了算法的勘探性能.實驗表明，對于單峰函數和多峰函數，改進的算法均能顯著提高算法的解的精度和算法的收斂速度，并提高了算法的勘探搜索能力.改進的單形進化算法能有效提高SSSE算法的性能，但對于部分函數的性能有待提高，因此后續的工作需要進一步考慮到一些特殊的函數，相信隨著上述問題的解決，將會有更精確、性能更完善的新型智能優化算法出現，為解決實際問題帶來便利.

將ISSSE應用于RBF神經網絡，并用UCI數據集對ISSSE-RBF驗證，實驗表明改進的單形進化算法具有更好的勘探和開采能力，能更好應用于神經網絡的結構參數的尋優.